4.3: Linear Approximations and Differentials
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Describe the linear approximation to a function at a point.
- Write the linearization of a given function.
- Draw a graph that illustrates the use of differentials to approximate the change in a quantity.
- Calculate the relative error and percentage error in using a differential approximation.
We have just seen how derivatives allow us to compare related quantities that are changing over time. In this section, we examine another application of derivatives: the ability to approximate functions locally by linear functions. Linear functions are the easiest functions with which to work, so they provide a useful tool for approximating function values. In addition, the ideas presented in this section are generalized later in the text when we study how to approximate functions by higher-degree polynomials Introduction to Power Series and Functions.
Linear Approximation of a Function at a Point
Consider a function
For example, consider the function
Figure
The actual value of
Therefore, the tangent line gives us a fairly good approximation of
whereas the value of the function at
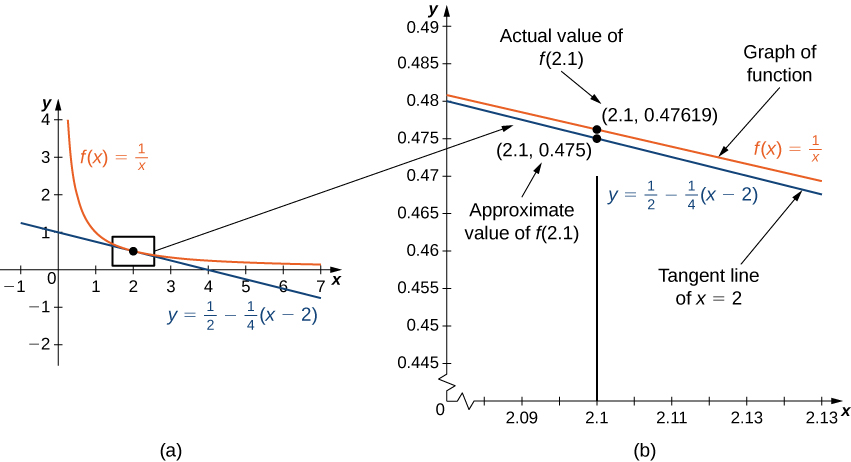
In general, for a differentiable function
We call the linear function
the linear approximation, or tangent line approximation, of
To show how useful the linear approximation can be, we look at how to find the linear approximation for
Example
Find the linear approximation of
Solution
Since we are looking for the linear approximation at
We need to find
Therefore, the linear approximation is given by Figure
Using the linear approximation, we can estimate
Analysis
Using a calculator, the value of
Exercise
Find the local linear approximation to
- Hint
-
- Answer
-
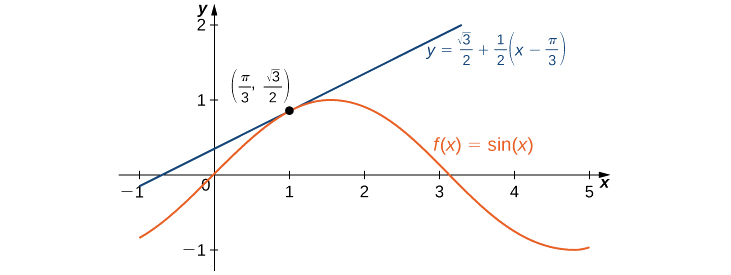
Example
Find the linear approximation of
Solution
First we note that since
We see that
Therefore, the linear approximation of
To estimate
Exercise
Find the linear approximation for
- Hint
-
- Answer
-
Linear approximations may be used in estimating roots and powers. In the next example, we find the linear approximation for
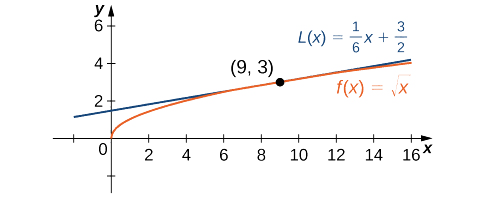
Example
Find the linear approximation of
Solution
The linear approximation at
Because
the linear approximation is given by Figure
We can approximate
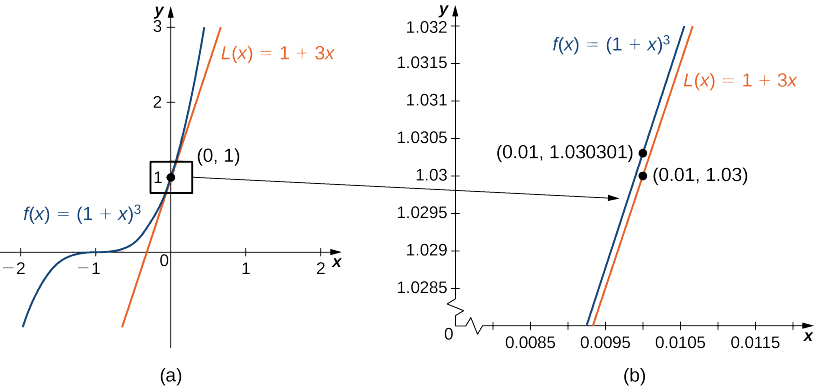
Exercise
Find the linear approximation of
- Hint
-
- Answer
-
Differentials
We have seen that linear approximations can be used to estimate function values. They can also be used to estimate the amount a function value changes as a result of a small change in the input. To discuss this more formally, we define a related concept: differentials. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.
When we first looked at derivatives, we used the Leibniz notation
It is important to notice that
This is the familiar expression we have used to denote a derivative. Equation
Example
For each of the following functions, find
Solution
The key step is calculating the derivative. When we have that, we can obtain
a. Since
When
b. Since
When
Exercise
For
- Hint
-
- Answer
-
We now connect differentials to linear approximations. Differentials can be used to estimate the change in the value of a function resulting from a small change in input values. Consider a function
Instead of calculating the exact change in
Therefore, if
That is,
In other words, the actual change in the function
Therefore, we can use the differential
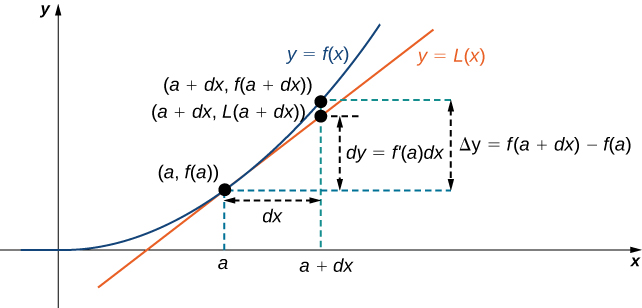
We now take a look at how to use differentials to approximate the change in the value of the function that results from a small change in the value of the input. Note the calculation with differentials is much simpler than calculating actual values of functions and the result is very close to what we would obtain with the more exact calculation.
Example
Let
Solution
The actual change in
The approximate change in
Exercise
For
- Hint
-
- Answer
-
Calculating the Amount of Error
Any type of measurement is prone to a certain amount of error. In many applications, certain quantities are calculated based on measurements. For example, the area of a circle is calculated by measuring the radius of the circle. An error in the measurement of the radius leads to an error in the computed value of the area. Here we examine this type of error and study how differentials can be used to estimate the error.
Consider a function
Since all measurements are prone to some degree of error, we do not know the exact value of a measured quantity, so we cannot calculate the propagated error exactly. However, given an estimate of the accuracy of a measurement, we can use differentials to approximate the propagated error
Unfortunately, we do not know the exact value
In the next example, we look at how differentials can be used to estimate the error in calculating the volume of a box if we assume the measurement of the side length is made with a certain amount of accuracy.
Example
Suppose the side length of a cube is measured to be
- Use differentials to estimate the error in the computed volume of the cube.
- Compute the volume of the cube if the side length is (i)
Solution
a. The measurement of the side length is accurate to within
The volume of a cube is given by
Using the measured side length of
Therefore,
b. If the side length is actually
If the side length is actually
Therefore, the actual volume of the cube is between
That is,
We see the estimated error
Exercise
Estimate the error in the computed volume of a cube if the side length is measured to be
- Hint
-
- Answer
-
The volume measurement is accurate to within
The measurement error
Example
An astronaut using a camera measures the radius of Earth as
Solution: If the measurement of the radius is accurate to within
Since the volume of a sphere is given by
Using the measured radius of
To estimate the relative error, consider
which simplifies to
The relative error is
Exercise
Determine the percentage error if the radius of Earth is measured to be
- Hint
-
Use the fact that
- Answer
-
Key Concepts
- A differentiable function
- For a function
is an approximation for the change in
- A measurement error
- To estimate the relative error of a particular quantity
Key Equations
- Linear approximation
- A differential
Glossary
- differential
- the differential
- differential form
- given a differentiable function
- linear approximation
- the linear function
- percentage error
- the relative error expressed as a percentage
- propagated error
- the error that results in a calculated quantity
- relative error
- given an absolute error
- tangent line approximation (linearization)
- since the linear approximation of
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.