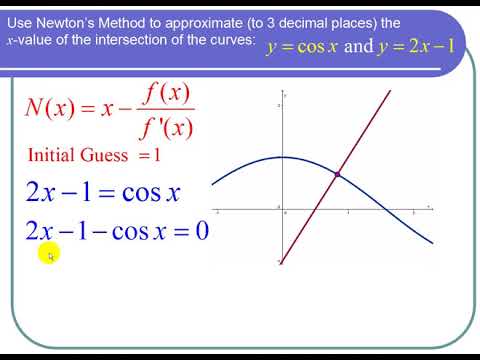
4.10: Newton’s Method
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Describe the steps of Newton’s method.
- Explain what an iterative process means.
- Recognize when Newton’s method does not work.
- Apply iterative processes to various situations.
In many areas of pure and applied mathematics, we are interested in finding solutions to an equation of the form
Describing Newton’s Method
Consider the task of finding the solutions of
No formula exists that allows us to find the solutions of
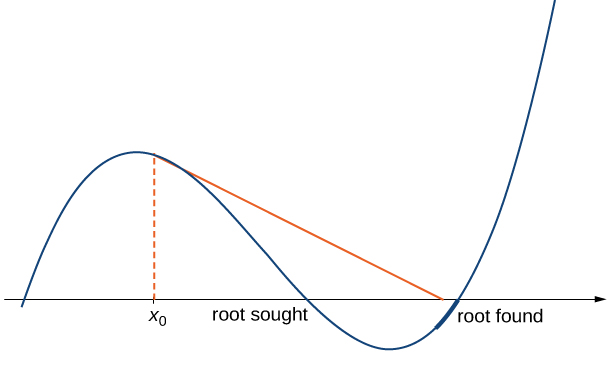
Newton’s method makes use of the following idea to approximate the solutions of
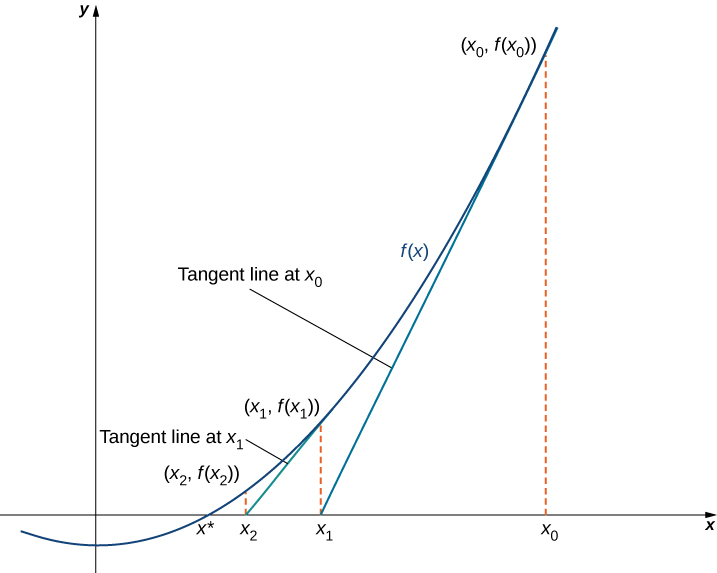
Now let’s look at how to calculate the approximations
Therefore,
Solving this equation for
Similarly, the point
In general, for
Next we see how to make use of this technique to approximate the root of the polynomial
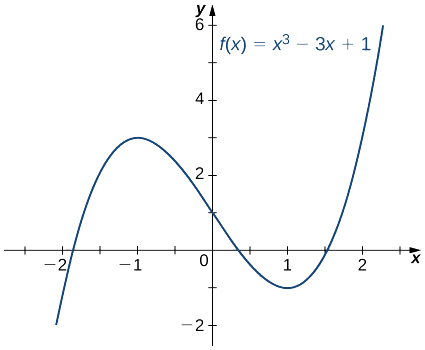
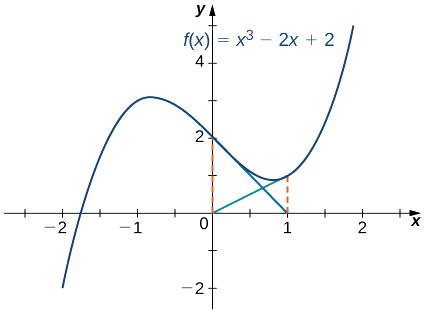
Example
Use Newton’s method to approximate a root of
Solution
From Figure
To find the next approximation,
Continuing in this way, we obtain the following results:
We note that we obtained the same value for
Exercise
Letting
- Hint
-
Use Equation
- Answer
-
Newton’s method can also be used to approximate square roots. Here we show how to approximate
Example
Use Newton’s method to approximate
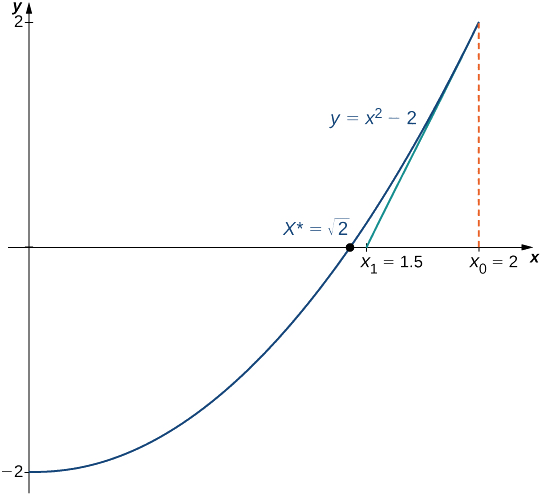
Solution
For
Therefore,
Continuing in this way, we find that
Since we obtained the same value for
Exercise
Use Newton’s method to approximate
- Hint
-
For
- Answer
-
When using Newton’s method, each approximation after the initial guess is defined in terms of the previous approximation by using the same formula. In particular, by defining the function
Failures of Newton’s Method
Typically, Newton’s method is used to find roots fairly quickly. However, things can go wrong. Some reasons why Newton’s method might fail include the following:
- At one of the approximations
- The approximations
- The approximations may fail to approach a root entirely. In Example
Example
Consider the function
Solution
For
In the next step,
Consequently, the numbers
Exercise
For
- Hint
-
Use Equation
- Answer
-
From Example
Other Iterative Processes
As mentioned earlier, Newton’s method is a type of iterative process. We now look at an example of a different type of iterative process.
Consider a function
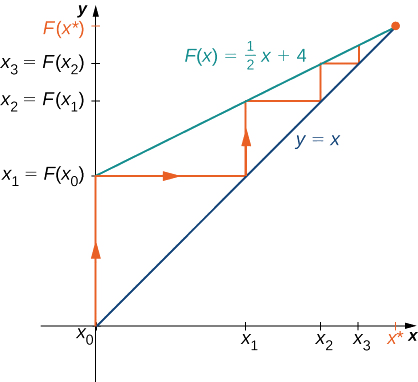
Example
Let
Solution
If
From this list, we conjecture that the values
Figure
Exercise
Consider the function
- Hint
-
Consider the point where the lines
- Answer
-
Iterative Processes and Chaos
Iterative processes can yield some very interesting behavior. In this section, we have seen several examples of iterative processes that converge to a fixed point. We also saw in Example
Some iterative processes yield what mathematicians call chaos. In this case, the iterative process jumps from value to value in a seemingly random fashion and never converges or settles into a cycle. Although a complete exploration of chaos is beyond the scope of this text, in this project we look at one of the key properties of a chaotic iterative process: sensitive dependence on initial conditions. This property refers to the concept that small changes in initial conditions can generate drastically different behavior in the iterative process.
Probably the best-known example of chaos is the Mandelbrot set (see Figure), named after Benoit Mandelbrot (1924–2010), who investigated its properties and helped popularize the field of chaos theory. The Mandelbrot set is usually generated by computer and shows fascinating details on enlargement, including self-replication of the set. Several colorized versions of the set have been shown in museums and can be found online and in popular books on the subject.

In this project we use the logistic map
where
as the function in our iterative process. The logistic map is a deceptively simple function; but, depending on the value of
To visualize the long-term behavior of the iterative process associated with the logistic map, we will use a tool called a cobweb diagram. As we did with the iterative process we examined earlier in this section, we first draw a vertical line from the point
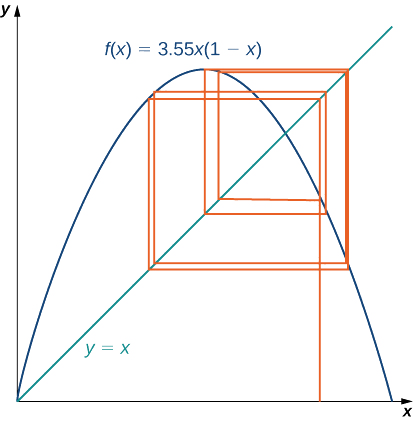
- Let
- What happens when
- For
- Now let
- Repeat the process for
Key Concepts
- Newton’s method approximates roots of
- Typically, Newton’s method is an efficient method for finding a particular root. In certain cases, Newton’s method fails to work because the list of numbers
- Any process in which a list of numbers
Glossary
- iterative process
- process in which a list of numbers
- Newton’s method
- method for approximating roots of
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.