21.8: Review Exercises

Chapter Review Exercises

Solve Systems of Linear Equations with Two Variables

Determine Whether an Ordered Pair is a Solution of a System of Equations.

In the following exercises, determine if the following points are solutions to the given system of equations.

1. \(\left\{ \begin{array} {l} x+3y=−9\\2x−4y=12 \end{array} \right.\)

ⓐ \((−3,−2)\)
ⓑ \((0,−3)\)

2. \(\left\{ \begin{array} {l} x+y=8\\y=x−4 \end{array} \right.\)

ⓐ \((6,2)\)
ⓑ \((9,−1)\)

Answer

ⓐ yes ⓑ no

Solve a System of Linear Equations by Graphing

In the following exercises, solve the following systems of equations by graphing.

3. \(\left\{ \begin{array} {l} 3x+y=6\\x+3y=−6 \end{array} \right.\)

4. \(\left\{ \begin{array} {l} x+4y=−1\\x=3 \end{array} \right.\)

Answer

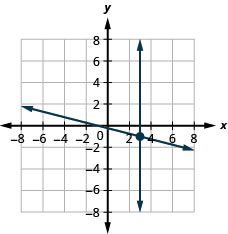
\((3,−1)\)

5. \(\left\{ \begin{array} {l} 2x−y=5\\4x−2y=10 \end{array} \right.\)

6. \(\left\{ \begin{array} {l} −x+2y=4\\y=\frac{1}{2}x−3 \end{array} \right.\)

Answer

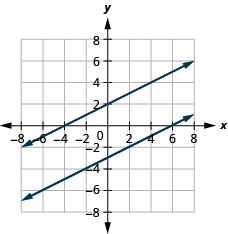
no solution

In the following exercises, without graphing determine the number of solutions and then classify the system of equations.

7. \(\left\{ \begin{array} {l} y=\frac{2}{5}x+2\\−2x+5y=10 \end{array} \right.\)

8. \(\left\{ \begin{array} {l} 3x+2y=6\\y=−3x+4 \end{array} \right.\)

Answer

one solution, consistent system, independent equations

9. \(\left\{ \begin{array} {l} 5x−4y=0\\y=\frac{5}{4}x−5 \end{array} \right.\)

Solve a System of Equations by Substitution

In the following exercises, solve the systems of equations by substitution.

10. \(\left\{ \begin{array} {l} 3x−2y=2\\y=\frac{1}{2}x+3 \end{array} \right.\)

Answer

\((4,5)\)

11. \(\left\{ \begin{array} {l} x−y=0\\2x+5y=−14 \end{array} \right.\)

12. \(\left\{ \begin{array} {l} y=−2x+7\\y=\frac{2}{3}x−1 \end{array} \right.\)

Answer

\((3,1)\)

13. \(\left\{ \begin{array} {l} y=−5x\\5x+y=6 \end{array} \right.\)

14. \(\left\{ \begin{array} {l} y=−\frac{1}{3}x+2\\x+3y=6 \end{array} \right.\)

Answer

infinitely many solutions

Solve a System of Equations by Elimination

In the following exercises, solve the systems of equations by elimination

15. \(\left\{ \begin{array} {l} x+y=12\\x−y=−10 \end{array} \right.\)

16. \(\left\{ \begin{array} {l} 3x−8y=20\\x+3y=1 \end{array} \right.\)

Answer

\((4,−1)\)

17. \(\left\{ \begin{array} {l} 9x+4y=2\\5x+3y=5 \end{array} \right.\)

18. \(\left\{ \begin{array} {l} \frac{1}{3}x−\frac{1}{2}y=1\\ \frac{3}{4}x−y=\frac{5}{2} \end{array} \right.\)

Answer

\((6,2)\)

19. \(\left\{ \begin{array} {l} −x+3y=8\\2x−6y=−20 \end{array} \right.\)

Choose the Most Convenient Method to Solve a System of Linear Equations

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

20. \(\left\{ \begin{array} {l} 6x−5y=27\\3x+10y=−24 \end{array} \right.\)

Answer

elimination

21. \(\left\{ \begin{array} {l} y=3x−9\\4x−5y=23 \end{array} \right.\)

Solve Applications with Systems of Equations

Solve Direct Translation Applications

In the following exercises, translate to a system of equations and solve.

22. Mollie wants to plant 200 bulbs in her garden, all irises and tulips. She wants to plant three times as many tulips as irises. How many irises and how many tulips should she plant?

Answer

50 irises and 150 tulips

23. Ashanti has been offered positions by two phone companies. The first company pays a salary of $22,000 plus a commission of $100 for each contract sold. The second pays a salary of $28,000 plus a commission of $25 for each contract sold. How many contract would need to be sold to make the total pay the same?

24. Leroy spent 20 minutes jogging and 40 minutes cycling and burned 600 calories. The next day, Leroy swapped times, doing 40 minutes of jogging and 20 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?

Answer

10 calories jogging and 10 calories cycling

25. Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and calculator. Troy bought four notebooks and five calculators for $116. Lisa bought two notebooks and three calculators for $68. Find the cost of each notebook and each thumb drive.

Solve Geometry Applications

In the following exercises, translate to a system of equations and solve.

26. The difference of two supplementary angles is 58 degrees. Find the measures of the angles.

Answer

119, 61

27. Two angles are complementary. The measure of the larger angle is five more than four times the measure of the smaller angle. Find the measures of both angles.

28. The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.

Answer

\(35°\) and \(55°\)

29. Becca is hanging a 28 foot floral garland on the two sides and top of a pergola to prepare for a wedding. The height is four feet less than the width. Find the height and width of the pergola.

30. The perimeter of a city rectangular park is 1428 feet. The length is 78 feet more than twice the width. Find the length and width of the park.

Answer

the length is 450 feet, the width is 264 feet

Solve Uniform Motion Applications

In the following exercises, translate to a system of equations and solve.

31. Sheila and Lenore were driving to their grandmother’s house. Lenore left one hour after Sheila. Sheila drove at a rate of 45 mph, and Lenore drove at a rate of 60 mph. How long will it take for Lenore to catch up to Sheila?

32. Bob left home, riding his bike at a rate of 10 miles per hour to go to the lake. Cheryl, his wife, left 45 minutes (34(34 hour) later, driving her car at a rate of 25 miles per hour. How long will it take Cheryl to catch up to Bob?

Answer

\(12\) an hour

33. Marcus can drive his boat 36 miles down the river in three hours but takes four hours to return upstream. Find the rate of the boat in still water and the rate of the current.

34. A passenger jet can fly 804 miles in 2 hours with a tailwind but only 776 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Answer

the rate of the jet is 395 mph, the rate of the wind is 7 mph

Solve Mixture Applications with Systems of Equations

Solve Mixture Applications with Systems of Equations

For the following exercises, translate to a system of equations and solve.

35. Lynn paid a total of $2,780 for 261 tickets to the theater. Student tickets cost $10 and adult tickets cost $15. How many student tickets and how many adult tickets did Lynn buy?

36. Priam has dimes and pennies in a cup holder in his car. The total value of the coins is $4.21. The number of dimes is three less than four times the number of pennies. How many dimes and how many pennies are in the cup?

Answer

41 dimes and 11 pennies

37. Yumi wants to make 12 cups of party mix using candies and nuts. Her budget requires the party mix to cost her $1.29 per cup. The candies are $2.49 per cup and the nuts are $0.69 per cup. How many cups of candies and how many cups of nuts should she use?

38. A scientist needs 70 liters of a 40% solution of alcohol. He has a 30% and a 60% solution available. How many liters of the 30% and how many liters of the 60% solutions should he mix to make the 40% solution?

Answer

\(46\frac{2}{3}\) liters of 30% solution, \(23\frac{1}{3}\) liters of 60% solution

Solve Interest Applications

For the following exercises, translate to a system of equations and solve.

39. Jack has $12,000 to invest and wants to earn 7.5% interest per year. He will put some of the money into a savings account that earns 4% per year and the rest into CD account that earns 9% per year. How much money should he put into each account?

40. When she graduates college, Linda will owe $43,000 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owes for one year was $1,585. What is the amount of each loan?

Answer

$29,000 for the federal loan, $14,000 for the private loan

Solve Systems of Equations with Three Variables

Solve Systems of Equations with Three Variables

In the following exercises, determine whether the ordered triple is a solution to the system.

41. \(\left\{ \begin{array} {l} 3x−4y−3z=2\\2x−6y+z=3\\2x+3y−2z=3 \end{array} \right.\)

ⓐ \((2,3,−1)\)
ⓑ \((3,1,3)\)

42. \(\left\{ \begin{array} {l} y=\frac{2}{3}x−2\\x+3y−z=15\\x−3y+z=−2 \end{array} \right.\)

ⓐ \((−6,5,\frac{1}{2})\)
ⓑ \((5,\frac{4}{3},−3)\)

Answer

ⓐ no ⓑ yes

Solve a System of Linear Equations with Three Variables

In the following exercises, solve the system of equations.

43. \(\left\{ \begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)

44. \(\left\{ \begin{array} {l} x+\frac{5}{2}y+z=−2\\2x+2y+\frac{1}{2}z=−4\\ \frac{1}{3}x−y−z=1 \end{array} \right.\)

Answer

\((−3,2,−4)\)

45. \(\left\{ \begin{array} {l} 5x+3y=−6\\2y+3z=−1\\7x+z=1 \end{array} \right.\)

46. \(\left\{ \begin{array} {l} 2x+3y+z=12\\x+y+z=9\\3x+4y+2z=20 \end{array} \right.\)

Answer

no solution

47. \(\left\{ \begin{array} {l} −x−3y+2z=14\\−x+2y−3z=−4\\3x+y−2z=6 \end{array} \right.\)

Solve Applications using Systems of Linear Equations with Three Variables

48. After attending a major league baseball game, the patrons often purchase souvenirs. If a family purchases 4 t-shirts, a cap and 1 stuffed animal their total is $135. A couple buys 2 t-shirts, a cap and 3 stuffed animals for their nieces and spends $115. Another couple buys 2 t-shirts, a cap and 1 stuffed animal and their total is $85. What is the cost of each item?

Answer

\(25, 20, 15\)

Solve Systems of Equations Using Matrices

Write the Augmented Matrix for a System of Equations.

Write each system of linear equations as an augmented matrix.

49. \(\left\{ \begin{array} {l} 3x−y=−1\\−2x+2y=5 \end{array} \right.\)

50. \(\left\{ \begin{array} {l} 4x+3y=−2\\x−2y−3z=7\\2x−y+2z=−6 \end{array} \right.\)

Answer

\(\left[ \begin{matrix} 4&3&0&−2\\1&−2&−3&7\\2&−1&2&−6 \end{matrix} \right]\)

Write the system of equations that that corresponds to the augmented matrix.

51. \(\left[ \begin{array} {cc|c} 2&−4&-2\\3&−3&-1 \end{array} \right]\)

52. \(\left[ \begin{array} {ccc|c} 1&0&−3&-1\\1&−2&0&-2\\0&−1&2&3 \end{array} \right]\)

Answer

\(\left\{ \begin{array} {l} x−3z=−1\\x−2y=−27\\−y+2z=3 \end{array} \right.\)

In the following exercises, perform the indicated operations on the augmented matrices.

53. \(\left[ \begin{array} {cc|c} 4&−6&-3\\3&2&1 \end{array} \right]\)

ⓐ Interchange rows 2 and 1.
ⓑ Multiply row 1 by 4.
ⓒ Multiply row 2 by 3 and add to row 1.

54. \(\left[ \begin{array} {ccc|c} 1&−3&−2&4\\2&2&−1&-3\\4&−2&−3&-1 \end{array} \right]\)

ⓐ Interchange rows 2 and 3.
ⓑ Multiply row 1 by 2.
ⓒ Multiply row 3 by −2−2 and add to row 2.

Answer

ⓐ \(\left[ \begin{matrix} 1&−3&−2&4\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]\)

ⓑ \(\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]\)

ⓒ \(\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\0&−6&−1&5 \end{matrix} \right]\)

Solve Systems of Equations Using Matrices

In the following exercises, solve each system of equations using a matrix.

55. \(\left\{ \begin{array} {l} 4x+y=6\\x−y=4 \end{array} \right.\)

56. \(\left\{ \begin{array} {l} 2x−y+3z=−3\\−x+2y−z=10\\x+y+z=5 \end{array} \right.\)

Answer

\((−2,5,−2)\)

57. \(\left\{ \begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1 \end{array} \right.\)

58. \(\left\{ \begin{array} {l} x+2y−3z=−1\\x−3y+z=1\\2x−y−2z=2 \end{array} \right.\)

Answer

no solution

59. \(\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.\)

Solve Systems of Equations Using Determinants

Evaluate the Determinant of a 2 × 2 Matrix

In the following exercise, evaluate the determinate of the square matrix.

60. \(\left[ \begin{matrix} 8&−4\\5&−3 \end{matrix} \right]\)

Answer

\(−4\)

Evaluate the Determinant of a 3 × 3 Matrix

In the following exercise, find and then evaluate the indicated minors.

61. \(\left| \begin{matrix} −1&−3&2\\4&−2&−1\\−2&0&−3 \end{matrix} \right|\); Find the minor ⓐ \(a_1\) ⓑ \(b_1\) ⓒ \(c_2\)

In the following exercise, evaluate each determinant by expanding by minors along the first row.

62. \(\left| \begin{matrix} −2&−3&−4\\5&−6&7\\−1&2&0 \end{matrix} \right|\)

Answer

\(21\)In the following exercise, evaluate each determinant by expanding by minors.

63. \(\left| \begin{matrix} 3&5&4\\−1&3&0\\−2&6&1 \end{matrix} \right|\)

Use Cramer’s Rule to Solve Systems of Equations

In the following exercises, solve each system of equations using Cramer’s rule

64. \(\left\{ \begin{array} {l} x−3y=−9\\2x+5y=4 \end{array} \right.\)

Answer

\((−3,2)\)

65. \(\left\{ \begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7 \end{array} \right.\)

66. \(\left\{ \begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3 \end{array} \right.\)

Answer

\((−3,2,3)\)

67. \(\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.\)

68. \(\left\{ \begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6 \end{array} \right.\)

Answer

inconsistent

Solve Applications Using Determinants

In the following exercises, determine whether the given points are collinear.

69. \((0,2)\), \((−1,−1)\), and \((−2,4)\)

Graphing Systems of Linear Inequalities

Determine Whether an Ordered Pair is a Solution of a System of Linear Inequalities

In the following exercises, determine whether each ordered pair is a solution to the system.

70. \(\left\{ \begin{array} {l} 4x+y>6\\3x−y\leq 12 \end{array} \right.\)

ⓐ \((2,−1)\)
ⓑ \((3,−2)\)

Answer

ⓐ yes ⓑ no

71. \(\left\{ \begin{array} {l} y>\frac{1}{3}x+2\\x−\frac{1}{4}y\leq 10 \end{array} \right.\)

ⓐ \((6,5)\)
ⓑ \((15,8)\)

Solve a System of Linear Inequalities by Graphing

In the following exercises, solve each system by graphing.

72. \(\left\{ \begin{array} {l} y<3x+1\\y\geq −x−2 \end{array} \right.\)

Answer

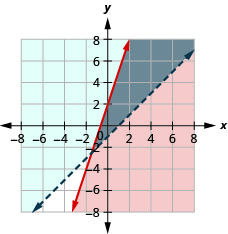
The solution is the grey region.

73. \(\left\{ \begin{array} {l} x−y>−1\\y<\frac{1}{3}x−2 \end{array} \right.\)

74. \(\left\{ \begin{array} {l} 2x−3y<6\\3x+4y\geq 12 \end{array} \right.\)

Answer

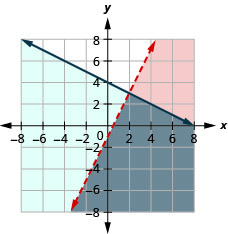
The solution is the grey region.

75. \(\left\{ \begin{array} {l} y\leq −\frac{3}{4}x+1\\x\geq −5 \end{array} \right.\)

76. \(\left\{ \begin{array} {l} x+3y<5\\y\geq -\frac{1}{3}x+6 \end{array} \right.\)

Answer

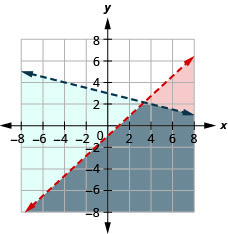
No solution.

77. \(\left\{ \begin{array} {l} y\geq 2x−5\\−6x+3y>−4 \end{array} \right.\)

Solve Applications of Systems of Inequalities

In the following exercises, translate to a system of inequalities and solve.

78. Roxana makes bracelets and necklaces and sells them at the farmers’ market. She sells the bracelets for $12 each and the necklaces for $18 each. At the market next weekend she will have room to display no more than 40 pieces, and she needs to sell at least $500 worth in order to earn a profit.

ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Should she display 26 bracelets and 14 necklaces?
ⓓ Should she display 39 bracelets and 1 necklace?

Answer

ⓐ \(\left\{ \begin{array} {l} b\geq 0\\ n\geq 0\\ b+n\leq 40\\12b+18n\geq 500 \end{array} \right.\)
ⓑ

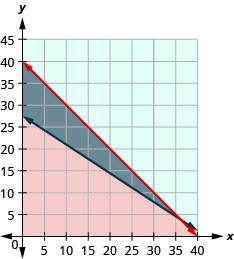
ⓒ yes
ⓓ no

79. Annie has a budget of $600 to purchase paperback books and hardcover books for her classroom. She wants the number of hardcover to be at least 5 more than three times the number of paperback books. Paperback books cost $4 each and hardcover books cost $15 each.

ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Can she buy 8 paperback books and 40 hardcover books?
ⓓ Can she buy 10 paperback books and 37 hardcover books?

Chapter Practice Test

In the following exercises, solve the following systems by graphing.

1. \(\left\{ \begin{array} {l} x−y=5\\x+2y=−4 \end{array} \right.\)

Answer

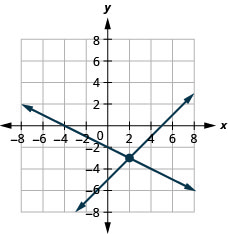
\((2,−3)\)

2. \(\left\{ \begin{array} {l} x−y>−2\\y\leq 3x+1 \end{array} \right.\)

In the following exercises, solve each system of equations. Use either substitution or elimination.

3. \(\left\{ \begin{array} {l} x+4y=6\\−2x+y=−3 \end{array} \right.\)

Answer

\((2,1)\)

4. \(\left\{ \begin{array} {l} −3x+4y=2\\5x−5y=−23 \end{array} \right.\)

5. \(\left\{ \begin{array} {l} x+y−z=−1\\2x−y+2z=8\\−3x+2y+z=−9 \end{array} \right.\)

Answer

\((2,−2,1)\)

Solve the system of equations using a matrix.

6. \(\left\{ \begin{array} {l} 2x+y=7\\x−2y=6 \end{array} \right.\)

7. \(\left\{ \begin{array} {l} −3x+y+z=−4\\−x+2y−2z=1\\2x−y−z=−1 \end{array} \right.\)

Answer

\((5,7,4)\)

Solve using Cramer’s rule.

8. \(\left\{ \begin{array} {l} 3x+y=−3\\2x+3y=6 \end{array} \right.\)

9. Evaluate the determinant by expanding by minors:

\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\)

Answer

\(99\)

In the following exercises, translate to a system of equations and solve.

10. Greg is paddling his canoe upstream, against the current, to a fishing spot 10 miles away. If he paddles upstream for 2.5 hours and his return trip takes 1.25 hours, find the speed of the current and his paddling speed in still water.

11. A pharmacist needs 20 liters of a 2% saline solution. He has a 1% and a 5% solution available. How many liters of the 1% and how many liters of the 5% solutions should she mix to make the 2% solution?

Answer

15 liters of 1% solution, 5 liters of 5% solution

12. Arnold invested $64,000, some at 5.5% interest and the rest at 9%. How much did he invest at each rate if he received $4,500 in interest in one year?

13. The church youth group is selling snacks to raise money to attend their convention. Amy sold 2 pounds of candy, 3 boxes of cookies and 1 can of popcorn for a total sales of $65. Brian sold 4 pounds of candy, 6 boxes of cookies and 3 cans of popcorn for a total sales of $140. Paulina sold 8 pounds of candy, 8 boxes of cookies and 5 can of popcorn for a total sales of $250. What is the cost of each item?

Answer

The candy cost $20; the cookies cost $5; and the popcorn cost $10.

14. The manufacturer of a granola bar spends $1.20 to make each bar and sells them for $2. The manufacturer also has fixed costs each month of $8,000.

ⓐ Find the cost function C when x granola bars are manufactured
ⓑ Find the revenue function R when x granola bars are sold.
ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.
ⓓ Find the break-even point. Interpret what the break-even point means.

15. Translate to a system of inequalities and solve.

Andi wants to spend no more than $50 on Halloween treats. She wants to buy candy bars that cost $1 each and lollipops that cost $0.50 each, and she wants the number of lollipops to be at least three times the number of candy bars.

ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Can she buy 20 candy bars and 40 lollipops?

Answer

ⓐ \(\left\{ \begin{array} {l} C\geq 0\\ L\geq 0\\ C+0.5L\leq 50 \\ L\geq 3C \end{array} \right.\)
ⓑ

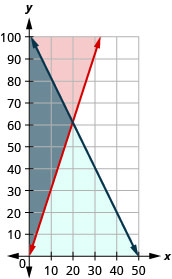
ⓒ no
ⓓ yes