7.12: Area, Surface Area and Volume Formulas
- Last updated
- Sep 30, 2020
- Save as PDF
- Page ID
- 51932

- Amy Lagusker
- College of the Canyons
( \newcommand{\kernel}{\mathrm{null}\,}\)
Area formulas
Let b = base
Let h = height
Let s = side
Let r = radius
|
Shape Name |
Shape |
Area Formula |
|---|---|---|
|
Rectangle |
 |
A=bh |
|
Square |
 |
A=bhA=s2 |
|
Parallelogram |
 |
A=bh |
|
Triangle |
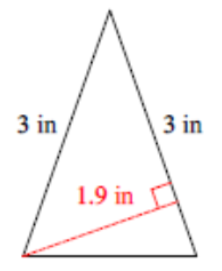
 |
A=12bh |
|
Circle |
 |
A=πr2 |
|
Trapezoid |
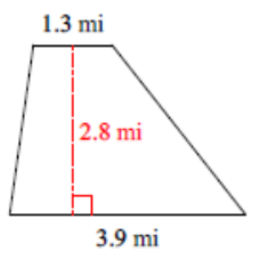
 |
A=12h(b1+b2) |
Surface Area Formulas
Variables:
SA = Surface Area
B = area of the base of the figure
P = perimeter of the base of the figure
h = height
s = slant height
r = radius
|
Geometric Figure |
Surface Area Formula |
Surface Area Meaning |
|---|---|---|
|
|
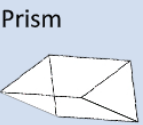
SA=2B+Ph |
Find the area of each face. Add up all areas. |
|
|
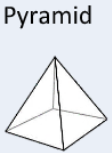
SA=B+12sP |
Find the area of each face. Add up all areas. |
|
|
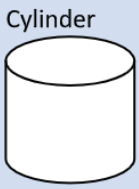
SA=2B+2πrh |
Find the area of the base, times 2, then add the areas to the areas of the rectangle, which is the circumference times the height. |
|
|
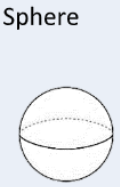
SA=4πr2 |
Find the area of the great circle and multiply it by 4. |
|
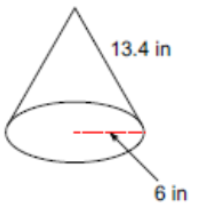
|
SA=B+πrS |
Find the area of the base and add the product of the radius times the slant height times PI. |
Volume Formulas
Variables:
SA = Surface Area
B = area of the base of the figure
P = perimeter of the base of the figure
h = height
s = slant height
r = radius
|
Geometric Figure |
Volume Formula |
Volume Meaning |
|---|---|---|
|
|
V=Bh |
Find the area of the base and multiply it by the height |
|
|
V=13Bh |
Find the area of the base and multiply it by 1/3 of the height. |
|
|
V=Bh |
Find the area of the base and multiply it by the height. |
|
|
V=43πr3 |
Find the area of the great circle and multiply it by the radius and then multiply it by 4/3. |
|
|
V=13Bh |
Find the area of the base and multiply it by 1/3 of the height. |
Example 7.12.1
Find the area of a circle with diameter of 14 feet.

Solution
A=πr2=π(7)2=49πfeet2=153.86feet2
Example 7.12.2
Find the area of a trapezoid with a height of 12 inches, and bases of 24 and 10 inches.

Solution
A=12h(b1+b2)=12(12)(24+10)=6(34)=204 inches2
Example 7.12.3
Find the surface area of a cone with a slant height of 8 cm and a radius of 3 cm.

Solution
SA=B+πrS=(πr2)+πrs=(π(32))+π(3)(8)=9π+24π=33πcm2=103.62cm2
Example 7.12.4
Find the surface area of a rectangular pyramid with a slant height of 10 yards, a base width (b) of 8 yards and a base length (h) of 12 yards.

Solution
SA=B+12sP=(bh)+12s(2b+2h)=(8)(12)+12(10)(2(8)+2(12))=96+12(10)(16+24)=96+5(40)=296 yards2
Example 7.12.5
Find the volume of a sphere with a diameter of 6 meters.

Solution
V=43πr3=43π(3)3=43(27π)=36π meters 3=113.04 meters 3
Partner Activity 1
- Find the area of a triangle with a base of 40 inches and a height of 60 inches.
- Find the area of a square with a side of 15 feet.
- Find the surface area of Earth, which has a diameter of 7917.5 miles. Use 3.14 for PI.
- Find the volume of a can a soup, which has a radius of 2 inches and a height of 3 inches. Use 3.14 for PI.
Practice Problems
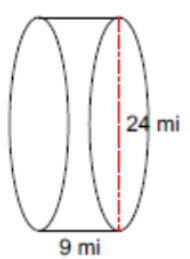
(Problems 1 – 4) Find the area of each circle with the given parameters. Use 3.14 for PI. Round your answer to the nearest tenth.
- Radius = 9 cm
- Diameter = 6 miles
- Radius = 8.6 cm
- Diameter = 14 meters
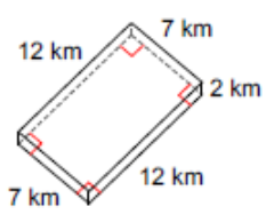
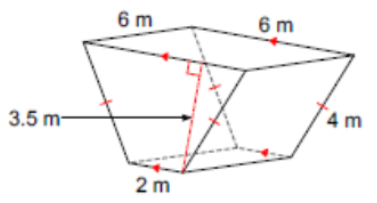
(Problems 5 – 8) Find the area of each polygon. Round answers to the nearest tenth.
(Problems 9 – 12) Name each figure.
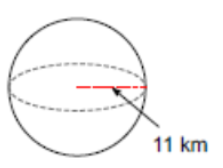
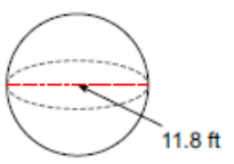
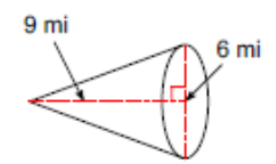
(Problems 13 – 17) Find the surface area of each figure. Leave your answers in terms of PI, if the answer contains PI. Round all other answers to the nearest hundredth.
(Problems 18 – 25) Find the volume of each figure. Leave your answers in terms of PI, for answers that contain PI. Round all other answers to the nearest hundredth.
Extension: Methods of Teaching Mathematics
Part 1
Assessments:
- What is the Difference between Formative and Summative Assessments? Which One is More Important?
- Formative Assessment Examples and When to Use Them
- Summative Assessment Examples and When to Use Them
Part 2
Write a Formative and Summative Assessment for Your Lesson Plan
Part 3
Make sure you are working on Khan Academy throughout the semester.