4.R: Further Applications of Trigonometry (Review)

4.1: Non-right Triangles: Law of Sines

For the exercises 1-5 assume \(\alpha \) is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). Solve each triangle, if possible. Round each answer to the nearest tenth.

1) \(\beta =50^{\circ}, a=105, b=45\)

Answer

Not possible

2) \(\alpha =43.1^{\circ}, a=184.2, b=242.8\)

3) Solve the triangle.

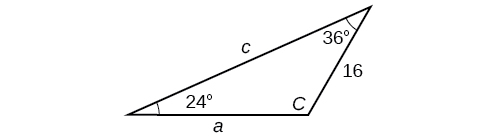
Answer

\(C=120^{\circ}, a=23.1, c=34.1\)

4) Find the area of the triangle.

Figure 4.

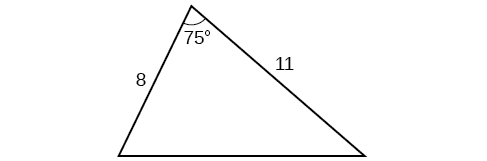
5) A pilot is flying over a straight Highway. He determines the angles of depression to two mile posts \(2.1\) km apart to be \(25^{\circ}\) and \(49^{\circ}\), as shown in the figure below. Find the distance of the plane from point \(A\) and the elevation of the plane.

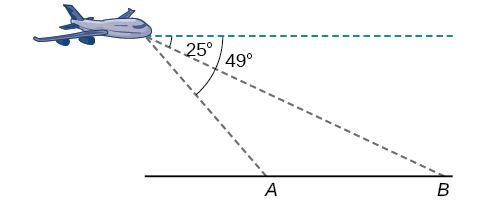
Answer

distance of the plane from point \(A:2.2\) km, elevation of the plane: \(1.6\) km

4.2: Non-right Triangles - Law of Cosines

1) Solve the triangle, rounding to the nearest tenth, assuming \(\alpha \) $$is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) s opposite side \(c: a=4, b=6,c=8\)$\mathrm{.}$

2) Solve the triangle in the Figure below, rounding to the nearest tenth.

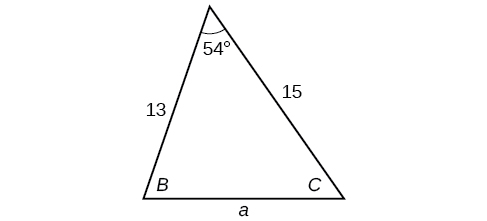
Answer

\(B=71.0^{\circ},C=55.0^{\circ},a=12.8\)

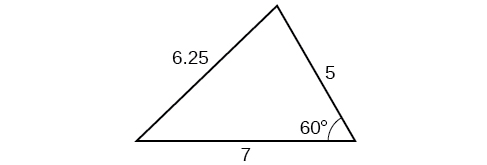
3) Find the area of a triangle with sides of length \(8.3\), \(6.6\), and \(9.1\).

4) To find the distance between two cities, a satellite calculates the distances and angle shown in the Figure below (not to scale). Find the distance between the cities. Round answers to the nearest tenth.

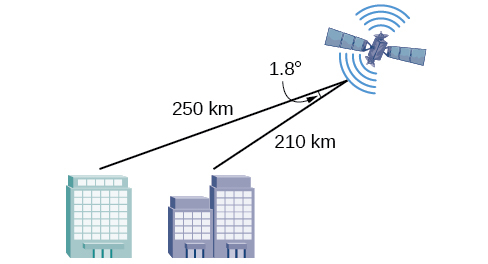
Answer

\(40.6\) km

4.3: Polar Coordinates

1) Plot the point with polar coordinates \(\left ( 3,\dfrac{\pi }{6} \right )\).

2) Plot the point with polar coordinates \(\left ( 5,\dfrac{-2\pi }{3} \right )\).

Answer

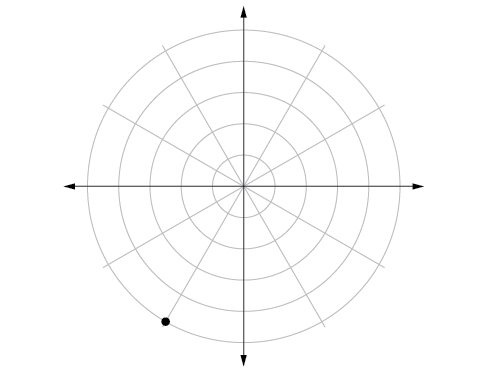
3) Convert \(\left ( 6,\dfrac{-3\pi }{4} \right )\) to rectangular coordinates.

4) Convert \(\left ( -2,\dfrac{3\pi }{2} \right )\) to rectangular coordinates.

Answer

\((0,2)\)

5) Convert \((7,-2)\) to polar coordinates.

6) Convert \((-9,-4)\) to polar coordinates.

Answer

\((9.8489,203.96^{\circ})\)

For the exercises 7-9, convert the given Cartesian equation to a polar equation.

7) \(x=-2\)

8) \(x^2+y^2=64\)

Answer

\(r=8\)

9) \(x^2+y^2=-2y\)

For the exercises 10-11, convert the given polar equation to a Cartesian equation.

10) \(r=7\cos \theta\)

Answer

\(x^2+y^2=7x\)

11) \(r=\dfrac{-2}{4\cos \theta +\sin \theta }\)

For the exercises 12-13, convert to rectangular form and graph.

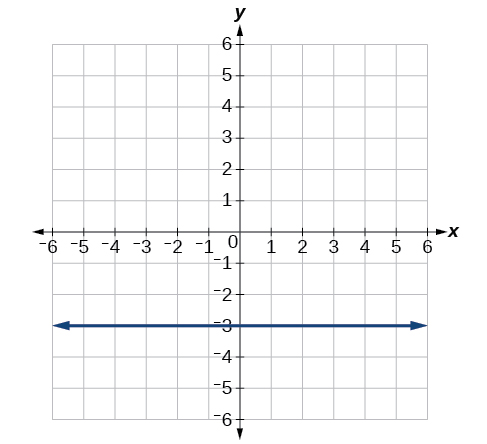
12) \(\theta =\dfrac{3\pi }{4}\)

Answer

\(y=-x\)

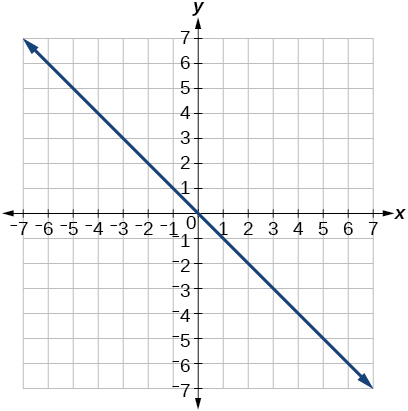
13) \(r=5\sec \theta\)

4.4: Polar Coordinates - Graphs

For the exercises 1-5, test each equation for symmetry.

1) \(r=4+4\sin \theta\)

Answer

symmetric with respect to the line \(\theta =\dfrac{\pi }{2}\)

2) \(r=7\)

3) Sketch a graph of the polar equation \(r=1-5\sin \theta\). Label the axis intercepts.

Answer

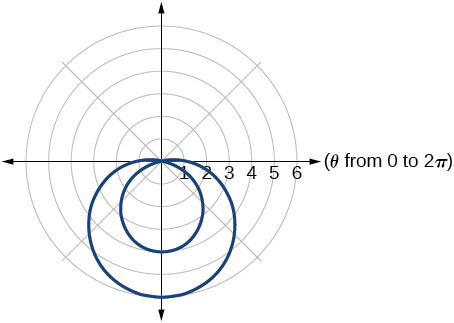
4) Sketch a graph of the polar equation \(r=5\sin (7\theta )\).

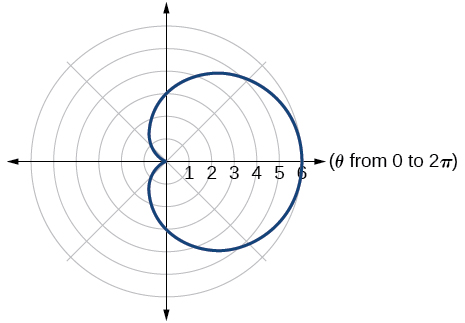
5) Sketch a graph of the polar equation \(r=3-3\cos \theta\)

Answer

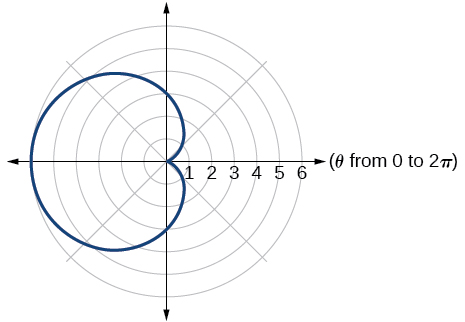
4.5: Polar Form of Complex Numbers

For the exercises 1-2, find the absolute value of each complex number.

1) \(-2+6i\)

2) \(4-3i\)

Answer

\(5\)

Write the complex number in polar form.

3) \(5+9i\)

4) \(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i\)

Answer

\(\mathrm{cis}\left (-\dfrac{\pi }{3} \right )\)

For the exercises 5-6, convert the complex number from polar to rectangular form.

5) \(z=5\mathrm{cis}\left (\dfrac{5\pi }{6} \right )\)

6) \(z=3\mathrm{cis}(40^{\circ})\)

Answer

\(2.3+1.9i\)

For the exercises 7-8, find the product \(z_1 z_2\) in polar form.

7) \(\begin{align*} z_1 &= 2\mathrm{cis}(89^{\circ})\\ z_2 &= 5\mathrm{cis}(23^{\circ}) \end{align*}\)

8) \(\begin{align*} z_1 &= 10\mathrm{cis}\left ( \dfrac{\pi }{6} \right )\\ z_2 &= 6\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}\)

Answer

\(60\mathrm{cis}\left ( \dfrac{\pi }{2} \right )\)

For the exercises 9-10, find the quotient \(\dfrac{z_1}{z_2}\) in polar form.

9) \(\begin{align*} z_1 &= 12\mathrm{cis}(55^{\circ})\\ z_2 &= 3\mathrm{cis}(18^{\circ}) \end{align*}\)

10) \(\begin{align*} z_1 &= 27\mathrm{cis}\left ( \dfrac{5\pi }{3} \right )\\ z_2 &= 9\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}\)

Answer

\(3\mathrm{cis}\left ( \dfrac{4\pi }{3} \right )\)

For the exercises 11-12, find the powers of each complex number in polar form.

11) Find \(z^4\) when \(z=2\mathrm{cis}(70^{\circ})\)

12) Find \(z^2\) when \(z=5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )\)

Answer

\(25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )\)

For the exercises 13-14, evaluate each root.

13) Evaluate the cube root of \(z\) when \(z=64\mathrm{cis}(210^{\circ})\).

14) Evaluate the square root of \(z\) when \(z=25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )\).

Answer

\(5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )\), \(5\mathrm{cis}\left ( \dfrac{7\pi }{4} \right )\)

For the exercises 15-16, plot the complex number in the complex plane.

15) \(6-2i\)

16) \(-1+3i\)

Answer

4.6: Parametric Equations

1) \(\begin{cases} & x(t)= 3t-1\\ & y(t)= \sqrt{t} \end{cases}\)

2) \(\begin{cases} & x(t)= -\cos t\\ & y(t)= 2\sin ^2t \end{cases}\)

Answer

\(x^2+\dfrac{1}{2}y=1\)

3) Parameterize (write a parametric equation for) each Cartesian equation by using \(x(t)=a\cos t\) and \(y(t)=b\sin t\) for \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\).

4) Parameterize the line from \((-2,3)\) to \((4,7)\) so that the line is at \((-2,3)\) at \(t=0\) and \((4,7)\) at \(t=1\).

Answer

\(\begin{cases} & x(t)= -2+6t\\ & y(t)= 3+4t \end{cases}\)

4.7: Parametric Equations - Graphs

For the exercises 1-, make a table of values for each set of parametric equations, graph the equations, and include an orientation; then write the Cartesian equation.

1) \(\begin{cases} & x(t)= 3t^2\\ & y(t)= 2t-1 \end{cases}\)

2) \(\begin{cases} & x(t)= e^t\\ & y(t)= -2e^{5t} \end{cases}\)

Answer

\(y=-2x^5\)

3) \(\begin{cases} & x(t)= 3\cos t\\ & y(t)= 2\sin t \end{cases}\)

4) A ball is launched with an initial velocity of \(80\) feet per second at an angle of \(40^{\circ}\) to the horizontal. The ball is released at a height of \(4\) feet above the ground.

1. Where is the ball after \(3\) seconds?
2. How long is the ball in the air?

Answer

1. \(\begin{cases} & x(t)= (80\cos (40^{\circ}))t\\ & y(t)= -16t^2+(80\sin (40^{\circ}))t+4 \end{cases}\)
2. The ball is 14 feet high and 184 feet from where it was launched.
3. \(3.3\) seconds

4.8: Vectors

For the exercises 1-2, determine whether the two vectors, \(\vecs u\) and \(\vecs v\), are equal, where \(\vecs u\) has an initial point \(P_1\) and a terminal point \(P_2\), and \(\vecs v\) has an initial point \(P_3\) and a terminal point \(P_4\).

1) \(P_1=(-1,4), P_2=(3,1), P_3=(5,5), P_4=(9,2)\)

2) \(P_1=(6,11), P_2=(-2,8), P_3=(0,-1), P_4=(-8,2)\)

Answer

not equal

For the exercises 3-4, use the vectors \(\vecs u=2\hat{\mathbf{i}}-\hat{\mathbf{j}}\), \(\vecs v=4\hat{\mathbf{i}}-3\hat{\mathbf{j}}\), and \(\vecs w=-2\hat{\mathbf{i}}+5\hat{\mathbf{j}}\) to evaluate the expression.

3) \( \vecs u-\vecs v \)

4) \( 2\vecs v-\vecs u+\vecs w \)

Answer

\(4\hat{\mathbf{i}}\)

For the exercises 5-6, find a unit vector in the same direction as the given vector.

5) \(\vecs a=8\hat{\mathbf{i}}-6\hat{\mathbf{j}}\)

6) \(\vecs b=-3\hat{\mathbf{i}}-\hat{\mathbf{j}}\)

Answer

\(-\dfrac{3\sqrt{10}}{10}\hat{\mathbf{i}}-\dfrac{\sqrt{10}}{10}\hat{\mathbf{j}}\)

For the exercises 7-11, calculate \(\vecs u\cdot \vecs v\)

7) \(\vecs u=-2\hat{\mathbf{i}}+\hat{\mathbf{j}}\) and \(\vecs v=3\hat{\mathbf{i}}+7\hat{\mathbf{j}}\)

8) \(\vecs u=\hat{\mathbf{i}}+4\hat{\mathbf{j}}\) and \(\vecs v=4\hat{\mathbf{i}}+3\hat{\mathbf{j}}\)

Answer

\(16\)

9) Given \(\vecs v=\left \langle -3,4 \right \rangle\) draw \(\vecs v\), \(2\vecs v\), and \(\dfrac{1}{2}\vecs v\).

10) Given the vectors shown in the Figure below, sketch \(\vecs u + \vecs v\), \(\vecs u − \vecs v\) and \(3\vecs v\).

Answer

11) Given initial point \(P_1=(3,2)\) and terminal point \(P_2=(-5,-1)\)$,$write the vector \(\vecs v\) in terms of \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\). Draw the points and the vector on the graph.

Practice Test

1) Assume \(\alpha \) is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). Solve the triangle, if possible, and round each answer to the nearest tenth, given \(\beta =68^{\circ},b=21,c=16\).

Answer

\(\alpha =67.1^{\circ}, \gamma =44.9^{\circ}, a=20.9\)

2) Find the area of the triangle in the Figure below. Round each answer to the nearest tenth.

3) A pilot flies in a straight path for \(2\) hours. He then makes a course correction, heading \(15^{\circ}\) to the right of his original course, and flies \(1\) hour in the new direction. If he maintains a constant speed of \(575\) miles per hour, how far is he from his starting position?

Answer

\(1712\) miles

4) Convert \((2,2)\) to polar coordinates, and then plot the point.

5) Convert \(\left ( 2,\dfrac{\pi }{3} \right )\) to rectangular coordinates.

Answer

\((1,\sqrt{3})\)

6) Convert the polar equation to a Cartesian equation: \(x^2+y^2=5y\).

7) Convert to rectangular form and graph:\(r=-3\csc θ\).

Answer

\(y=-3\)

8) Test the equation for symmetry: \(r=-4\sin(2\theta )\).

9) Graph \(r=3+3\cos \theta\).

Answer

10) Graph \(r=3-5\sin \theta\).

11) Find the absolute value of the complex number \(5-9i\).

Answer

\(\sqrt{106}\)

12) Write the complex number in polar form: \(4+i\).

13) Convert the complex number from polar to rectangular form: \(z=5\mathrm{cis}\left ( \dfrac{2\pi }{3} \right )\)

Answer

\(\dfrac{-5}{2}+i\dfrac{5\sqrt{3}}{2}\)

14) \(z_1 z_2\)

15) \(\dfrac{z_1}{z_2}\)

Answer

\(4\mathrm{cis}(21^{\circ})\)

16) \((z_2)^3\)

17) \(\sqrt{z_1}\)

Answer

\(2\sqrt{2}\mathrm{cis}(18^{\circ}), 2\sqrt{2}\mathrm{cis}(198^{\circ})\)

18) Plot the complex number \(-5-i\) in the complex plane.

19) Eliminate the parameter \(t\) to rewrite the following parametric equations as a Cartesian equation: \(\begin{cases} & x(t)= t+1\\ & y(t)= 2t^2 \end{cases}\)

Answer

\(y=2(x-1)^2\)

20) Parameterize (write a parametric equation for) the following Cartesian equation by using \(x(t)=a\cos t\) and \(y(t)=b\sin t : \dfrac{x^2}{36}+\dfrac{y^2}{100}=1\)

21) Graph the set of parametric equations and find the Cartesian equation: \(\begin{cases} & x(t)= -2\sin t\\ & y(t)= 5\cos t \end{cases}\)

Answer

22) A ball is launched with an initial velocity of \(95\) feet per second at an angle of \(52^{\circ}\) to the horizontal. The ball is released at a height of \(3.5\) feet above the ground.

1. Where is the ball after \(2\) seconds?
2. How long is the ball in the air?

For the exercises 23-26, use the vectors \(\vecs u = \hat{\mathbf{i}} − 3\hat{\mathbf{j}}\) and \(\vecs v = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}\).

23) Find \(2\vecs u − 3\vecs v\).

Answer

\(-4\hat{\mathbf{i}}-15\hat{\mathbf{j}}\)

24) Calculate \(\vecs u\cdot \vecs v\).

25) Find a unit vector in the same direction as \(\vecs v\).

Answer

\(\dfrac{2\sqrt{3}}{13}\hat{\mathbf{i}}+\dfrac{3\sqrt{3}}{13}\hat{\mathbf{j}}\)

26) Given vector \(\vecs v\) has an initial point \(P_1=(2,2)\) and terminal point \(P_2=(-1,0)\), write the vector \(\vecs u\cdot \vecs v\).

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.