2.3: Set Operations

Commonly sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.

Union, Intersection, and Complement

The union of two sets contains all the elements contained in either set (or both sets).

The union is notated \(A \cup B\)

More formally, \(x \in A \cup B\) if \(x \in A\) or \(x \in B\) (or both)

The intersection of two sets contains only the elements that are in both sets.

The intersection is notated \(A \cap B\)

More formally, \(x \in A \cap B\) if \(x \in A\) and \(x \in B\)

If A is a subset of the universal set U, then the complement of A is the set of elements that are elements of U, but are not in the set A.

The complement is notated \(A'\), or \(A^{c}\), or sometimes \(\sim A\).

More formally, \(x \in A'\) if \(x \in U\) and \(x \notin A\)

The difference of sets A and B is the set of elements in A that are not in B.

The difference is notated \(A - B\)

More formally, \(x \in A - B\) if \(x \in A\) and \(x \notin B\)

Example 1

Consider the sets:

\(\quad U=\{\text{red, orange, yellow, green, blue, indigo, purple}\} \quad A=\{\text { red, green, blue }\} \quad B=\{\text { red, yellow, orange }\} \quad C=\{\text { red, orange, yellow, green, blue, purple }\}\)

1. Find \(A \cup B\)
2. Find \(A \cap B\)
3. Find \(A' \cap C\)
4. Find \(A - B\)

Solution

a) The union contains all the elements in either set: \(A \cup B=\{\text { red, green, blue, yellow, orange }\}\)

Notice we only list red once.

b) The intersection contains all the elements in both sets: \(A \cap B=\{\text { red }\}\)

c) Here we're looking for all the elements that are not in set \(A\) and are also in \(C\).

\(A' \cap C=\{\text { orange, yellow, purple }\}\)

d) Here we want to find all the elements that are in the set \(A\) that are not in \(B\).

\(A - B=\{\text { green, blue}\}\)

Try it Now 1

Using the sets from the previous example, find \(A \cup C\) and \(B' \cap A\)

Answer

\(A \cup C=\{\text { red, orange, yellow, green, blue purple }\}\)

\(B' \cap A=\{\text { green, blue }\}\)

Example 2

Suppose the universal set is \(U=\) all whole numbers from \(1\) to \(9 .\) If \(A=\{1,2,4\}\), then

\(A'=\{3,5,6,7,8,9\}\)

As we saw earlier with the expression \(A^{c} \cap C,\) set operations can be grouped together. Grouping symbols can be used like they are with arithmetic - to force an order of operations.

Example 3

Suppose

\(H=\{\text { cat, dog, rabbit, mouse }\}, F=\{\text { dog, cow, duck, pig, rabbit }\} \quad W=\{\text { duck, rabbit, deer, frog, mouse }\}\)

1. Find \((H \cap F) \cup W\)
2. Find \(H \cap(F \cup W)\)
3. Find \((H \cap F)' \cap W\)

Solution

a) We start with the intersection: \(H \cap F=\{\text { dog, rabbit }\}\)

Now we union that result with \(W:(H \cap F) \cup W=\{\text{dog, duck, rabbit, deer, frog, mouse }\}\)

b) We start with the union: \(F \cup W=\{\text{dog, cow, rabbit, duck, pig, deer, frog, mouse }\}\)

Now we intersect that result with \(H: H \cap(F \cup W)=\{\text { dog, rabbit, mouse }\}\)

c) We start with the intersection: \(H \cap F=\{\mathrm{dog}, \text { rabbit }\}\)

Now we want to find the elements of \(W\) that are not in \(\mathrm{H} \cap F\)

\((H \cap F)' \cap W=\{\text { duck, deer, frog, mouse }\}\)

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18^th century. These illustrations now called Venn Diagrams.

Venn Diagram

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets.

Basic Venn diagrams can illustrate the interaction of two or three sets.

Example 4

Create Venn diagrams to illustrate \(A \cup B, A \cap B,\) and \(A' \cap B\)

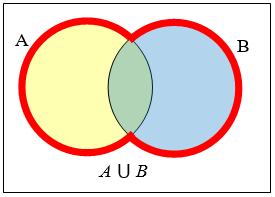\(A \cup B\) contains all elements in either set.

\(A \cup B\) contains all elements in either set.

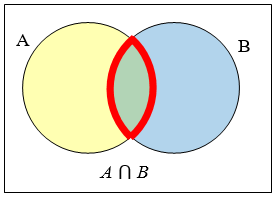
\(A \cap B\) contains only those elements in both sets - in the overlap of the circles.

Example 5

Use a Venn diagram to illustrate \((H \cap F)' \cap W\)

We'll start by identifying everything in the set \(\mathrm{H} \cap F\)

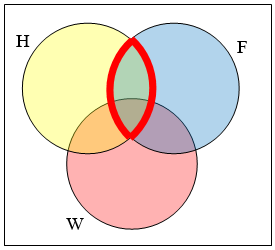
Now, \((H \cap F)' \cap W\) will contain everything not in the set identified above that is also in set \(W\)

Example 6

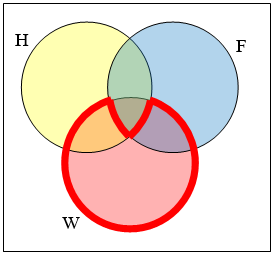
Create an expression to represent the outlined part of the Venn diagram shown.

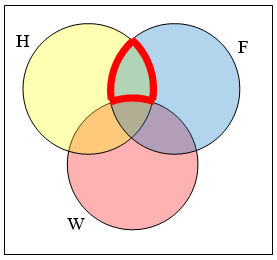The elements in the outlined set are in sets \(\mathrm{H}\) and \(F\), but are not in set \(W\). So we could represent this set as \(H \cap F \cap W\)

Try it Now 2

Create an expression to represent the outlined portion of the Venn diagram shown

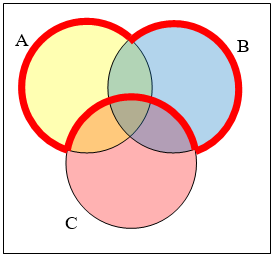
Answer

\(A \cup B \cap C'\)

DeMorgan's Laws

If A and B are sets, then \((A \cup B\))' = \(A' \cap B'\) and \((A \cap B\))' = \(A' \cup B'\)

Example 7

Let \(A=\{1,2,3,4,5\}\) and \(B=\{2,4,6,8,10\}\), with universal set \(U=\{1,2,3,4,5,6,7,8,9,10\}\). Verify one of the above laws by showing that \((A \cup B\))' = \(A' \cap B'\)

Solution

\(A \cup B = \{1,2,3,4,5,6,8,10\}\) and so \(A \cup B' = \{7,9\}\).

\(A'=\{6,7,8,9,10\}\) and \(B'=\{1,3,5,7,9\}\), so \(A' \cap B' = \{7,9\}\). This confirms that both sides are equal and \((A \cup B\))' = \(A' \cap B'\).