7.1: Linear Equations

Populations of people, animals, and items are growing all around us. By understanding how things grow, we can better understand what to expect in the future. In this chapter, we focus on time-dependent change.

Graphing a Line from an Equation

Equations whose graphs are straight lines are called linear equations. The following are some examples of linear equations:

\(2 x-3 y=6, \quad 3 x=4 y-7, \quad y=2 x-5, \quad 2 y=3, \quad \text { and } \quad x-2=0\)

A line is completely determined by two points. Therefore, to graph a linear equation we need to find the coordinates of two points. This can be accomplished by choosing an arbitrary value for x or y and then solving for the other variable.

Example \(\PageIndex{1}\)

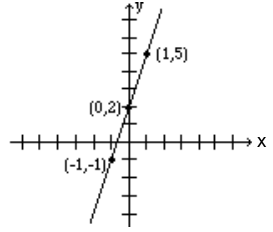
Graph the line: \(y = 3x + 2\)

Solution

We need to find the coordinates of at least two points. We arbitrarily choose x = - 1, x = 0, and x = 1.

• If x = -1, then y = 3(-1) + 2 or -1. Therefore, (-1, -1) is a point on this line.
• If x = 0, then y = 3(0) + 2 or y = 2. Hence the point (0, 2).
• If x = 1, then y = 5, and we get the point (1, 5).

Below, the results are summarized, and the line is graphed.

x	-1	0	1
y	-1	2	5

Example \(\PageIndex{2}\)

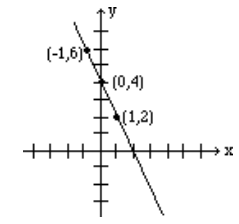
Graph the line: \(2x + y = 4\)

Solution

Again, we need to find coordinates of at least two points.

We arbitrarily choose x = -1, x = 0, and y = 2.

• If x = -1, then 2(-1) + y = 4 which results in y = 6. Therefore, (-1, 6) is a point on this line.
• If x = 0, then 2(0) + y = 4, which results in y = 4. Hence the point (0, 4).
• If y = 2, then 2x + 2 = 4, which yields x = 1, and gives the point (1, 2).

The table below shows the points, and the line is graphed.

x	-1	0	1
y	6	4	2

Intercepts

The points at which a line crosses the coordinate axes are called the intercepts.
When graphing a line by plotting two points, using the intercepts is often preferred because they are easy to find.

• To find the value of the x-intercept, we let y = 0
• To find the value of the y-intercept, we let x = 0.

Example \(\PageIndex{3}\)

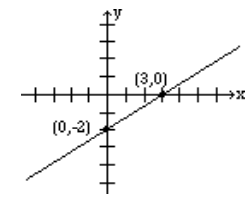
Find the intercepts of the line: \(2x - 3y = 6\), and graph.

Solution

To find the x-intercept, let y = 0 in the equation, and solve for x.

\[\begin{align*} 2x - 3(0) &= 6 \\[4pt] 2x - 0 &= 6 \\[4pt] 2x &= 6 \\[4pt] x &= 3 \end{align*}\]

Therefore, the x-intercept is the point (3,0).

To find the y-intercept, let x = 0 in the equation, and solve for y.

\[\begin{align*} 2(0) - 3y &= 6 \\[4pt] 0 - 3y &= 6 \\[4pt] -3y &= 6 \\[4pt] y &= -2 \end{align*}\]

Therefore, the y-intercept is the point (0, -2).

To graph the line, plot the points for the x-intercept (3,0) and the y-intercept (0, -2), and use them to draw the line.

Horizontal and Vertical Lines

When an equation of a line has only one variable, the resulting graph is a horizontal or a vertical line.

• The graph of the line \(x = a\), where \(a\) is a constant, is a vertical line that passes through the point \((a, 0)\). Every point on this line has the x-coordinate equal to a, regardless of the y-coordinate.
• The graph of the line \(y = b\), where \(b\) is a constant, is a horizontal line that passes through the point \((0, b)\). Every point on this line has the y-coordinate equal to b, regardless of the x-coordinate.

Example \(\PageIndex{4}\)

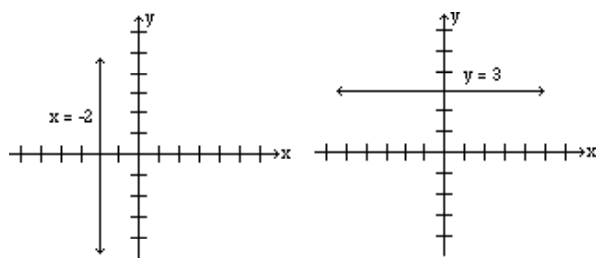
Graph the lines: x = -2 , and y = 3.

Solution

The graph of the line x = -2 is a vertical line that has the x-coordinate -2 no matter what the y-coordinate is. The graph is a vertical line passing through point (-2, 0).

The graph of the line y = 3, is a horizontal line that has the y-coordinate 3 regardless of what the x-coordinate is. Therefore, the graph is a horizontal line that passes through point (0, 3).

Note: Most students feel that the coordinates of points must always be integers. This is not true, and in real life situations, not always possible. Do not be intimidated if your points include numbers that are fractions or decimals.

Slope

So far we have learned how to graph a line by choosing two points on the line. The graph of a line can also be determined if one point and the "steepness" of the line is known. The number that refers to the steepness or inclination of a line is called the slope of the line.

From previous math courses, you may remember slope as the "rise over run," or "the vertical change over the horizontal change" and have often seen it expressed as:

\[\frac{\text {rise}}{\text {run}}, \frac{\text {vertical change}}{\text {horizontal change}}, \frac{\Delta y}{\Delta x} \text { etc. } \nonumber\]

Definition: Slope

If (\(x_1\), \(y_1\)) and (\(x_2\), \(y_2\)) are two different points on a line, the slope of the line is

\[\text{slope}=m=\frac{y_2-y_1}{x_2-x_1} \label{slope}\]

Example \(\PageIndex{5}\)

Find the slope of the line passing through points (−2, 3) and (4, −1), and graph the line.

Solution

Let (\(x_1\), \(y_1\)) = (−2, 3) and (\(x_2\), \(y_2\)) = (4, −1), then the slope (via Equation \ref{slope}) is

\(m = \frac{-1-3}{4-(-2)} = \frac{-4}{6} = -\frac{2}{3}\)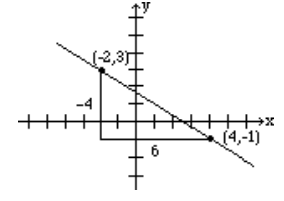

To give the reader a better understanding, both the vertical change, -4, and the horizontal change, 6, are shown in the above figure.

When two points are given, it does not matter which point is denoted as (\(x_1\), \(y_1\)) and which (\(x_2\), \(y_2\)). The value for the slope will be the same.

In Example \(\PageIndex{5}\), if we instead choose (\(x_1\), \(y_1\)) = (4, −1) and (\(x_2\), \(y_2\)) = (−2, 3), then we will get the same value for the slope as we obtained earlier.

The steps involved are as follows.

\[m = \frac{3-(-1)}{-2-4} = \frac{4}{-6} = -\frac{2}{3} \nonumber \]

The student should further observe that

• if a line rises when going from left to right, then it has a positive slope. In this situation, as the value of \(x\) increases, the value of \(y\) also increases
• if a line falls going from left to right, it has a negative slope; as the value of \(x\) increases, the value of \(y\) decreases.

Example \(\PageIndex{6}\)

Find the slope of the line that passes through the points (2, 3) and (2, −1), and graph.

Solution

Let (\(x_1\), \(y_1\)) = (2, 3) and (\(x_2\), \(y_2\)) = (2, −1) then the slope is

\[m = \frac{-1-3}{2-2}=\frac{4}{0}=\text{undefined.} \nonumber\]

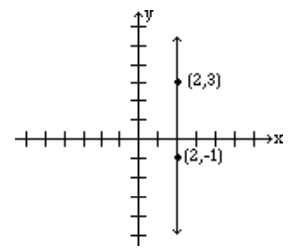
Note: The slope of a vertical line is undefined.

Example \(\PageIndex{7}\)

Find the slope of the line that passes through the points (−1, −4) and (3, −4)

Solution

Let (\(x_1\), \(y_1\)) = (−1, −4) and (\(x_2\), \(y_2\)) = (3, −4), then the slope is

\[ m = \frac{-4-(-4)}{3-(-1)} = \frac{0}{4} = 0 \nonumber \]

Note: The slope of a horizontal line is 0

Example \(\PageIndex{8}\)

Graph the line that passes through the point (1, 2) and has slope \(-\frac{3}{4}\).

Solution

Slope equals \(\frac{\text{rise}}{\text{run}}\). The fact that the slope is \(\frac{-3}{4}\), means that for every rise of -3 units (fall of 3 units) there is a run of 4. So if from the given point (1, 2) we go down 3 units and go right 4 units, we reach the point (5, -1). The graph is obtained by connecting these two points.

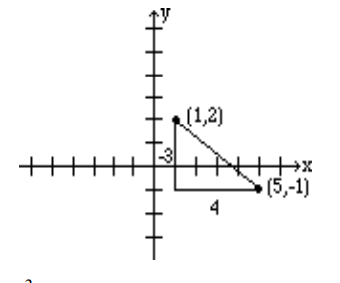
Alternatively, since \(\frac{3}{-4}\) represents the same number, the line can be drawn by starting at the point (1,2) and choosing a rise of 3 units followed by a run of -4 units. So from the point (1, 2), we go up 3 units, and to the left 4, thus reaching the point (-3, 5) which is also on the same line. See figure below.

Example \(\PageIndex{9}\)

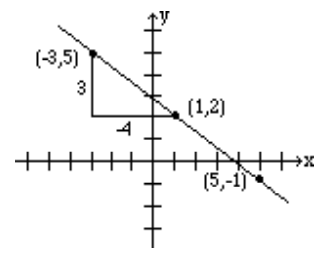
Find the slope of the line \(2x + 3y = 6\).

Solution

In order to find the slope of this line, we will choose any two points on this line.

Again, the selection of \(x\) and \(y\) intercepts seems to be a good choice. The \(x\)-intercept is (3, 0), and the \(y\)-intercept is (0, 2). Therefore, the slope is

\[m = \frac{2-0}{0-3} =-\frac{2}{3}.\]

The graph below shows the line and the \(x\)-intercepts and \(y\)-intercepts:

Example \(\PageIndex{10}\)

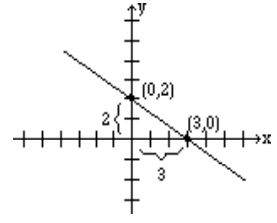
Find the slope of the line \(y = 3x + 2\).

Solution

We again find two points on the line, e.g., (0, 2) and (1, 5). Therefore, the slope is

\[m =\frac{5-2}{1-0} = \frac{3}{1} = 3. \nonumber\]

Look at the slopes and the \(y\)-intercepts of the following lines.

The line	slope	\(y\)-intercept
\(y=3x+2\)	3	2
\(y=-2x+5\)	-2	5
\(y=\frac{3}{2}x-4\)	\(\frac{3}{2}\)	-4

It is no coincidence that when an equation of the line is solved for \(y\), the coefficient of the \(x\) term represents the slope, and the constant term represents the \(y\)-intercept.

In other words, for the line \(y = mx + b\), \(m\) is the slope, and \(b\) is the \(y\)-intercept.

Example \(\PageIndex{11}\)

Determine the slope and \(y\)-intercept of the line \(2x + 3y = 6\).

Solution

We solve for \(y\):

\begin{align*}
&2 x+3 y=6 \nonumber \\
&3 y=-2 x+6 \nonumber \\
&y=(-2 / 3) x+2 \nonumber
\end{align*}

The slope = the coefficient of the \(x\) term = − 2/3.

The \(y\)-intercept = the constant term = 2.

So far, we were given an equation of a line and were asked to give information about it. For example, we were asked to find points on the line, find its slope and even find intercepts. Now we are going to reverse the process. That is, we will be given either two points, or a point and the slope of a line, and we will be asked to find its equation.

An equation of a line can be written in three forms, the slope-intercept form, the point-slope form, or the standard form. We will discuss each of them in this section.

A line is completely determined by two points, or by a point and slope. The information we are given about a particular line will influence which form of the equation is most convenient to use. Once we know any form of the equation of a line, it is easy to re-express the equation in the other forms if needed.

The Slope-Intercept Form of a Line: \(y = mx + b\)

In the last section we learned that the equation of a line whose slope = \(m\) and
\(y\)-intercept = \(b\) is \[\mathbf{y=mx+b}.\] This is called the slope-intercept form of the line and is the most commonly used form.

Example \(\PageIndex{12}\)

Find an equation of a line whose slope is 5, and \(y\)-intercept is 3.

Solution

Since the slope is \(m = 5\), and the \(y\)- intercept is \(b = 3\), the equation is \(y = 5x + 3\).

Example \(\PageIndex{13}\)

Find the equation of the line that passes through the point (\(2, 7\)) and has slope \(3\).

Solution

Since \(m = 3\), the partial equation is \(y = 3x + b\).

Now \(b\) can be determined by substituting the point (\(2, 7\)) in the equation \(y = 3x + b\).

\begin{aligned}
&7=3(2)+b \nonumber \\
&b=1 \nonumber
\end{aligned}

Therefore, the equation is \(y = 3x + 1\).

Example \(\PageIndex{14}\)

Find an equation of the line that passes through the points (-1, 2), and (1, 8).

Solution

\(m=\frac{8-2}{1-(-1)}=\frac{6}{2}=3\). So the partial equation is \(y = 3x + b\).

We can use either of the two points (-1, 2) or (1, 8), to find \(b\). Substituting (-1, 2) gives

\begin{aligned}
&2=3(-1)+b \nonumber \\
&5=b \nonumber
\end{aligned}

So the equation is \(y = 3x +5\).

Example \(\PageIndex{15}\)

Find an equation of the line that has \(x\)-intercept 3, and \(y\)-intercept 4.

Solution

\(x\)-intercept = 3, and \(y\)-intercept = 4 correspond to the points (3, 0), and (0, 4), respectively.

\[ m=\frac{4-0}{0-3} = -\frac{4}{3} \nonumber \]

We are told the \(y\)-intercept is 4; thus \(b\) = 4

Therefore, the equation is \(y = -\frac{4}{3} x + 4\).

The Point-Slope Form of a Line: \(y - y_1 = m(x - x_1)\)

The point-slope form is useful when we know two points on the line and want to find the equation of the line.

Let \(L\) be a line with slope \(m\), and known to contain a specific point (\(x_1\), \(y_1\)). If (\(x, y\)) is any other point on the line \(L\), then the definition of a slope leads us to the point-slope form or point-slope formula.

The slope is \( \frac{y-y_1}{x-x_1}= m\)

Multiplying both sides by (\(x-x_1\)) gives the point-slope form:

\[\mathbf{y - y_1 = m(x - x_1)} \]

Example \(\PageIndex{16}\)

Find the point-slope form of the equation of a line that has slope 1.5 and passes through the point (12,4).

Solution

Substituting the point \((x_1,y_1) = (12,4)\) and \(m= 1.5\) in the point-slope formula, we get

\[\mathbf{y - y_1 = m(x - x_1)} \nonumber \]

\[y - 4 = 1.5(x - 12) \nonumber \]

The student may be tempted to simplify this into the slope intercept form \(y = mx + b\). But since the problem specifically requests point-slope form we will not simplify it.

The Standard Form of a Line: \(Ax + By = C\)

Another useful form of the equation of a line is the standard form.

If we know the equation of a line in point-slope form, \(y - y_1 = m(x - x_1)\), or if we know the equation of the line in slope-intercept form \(y = mx + b\), we can simplify the formula to have all terms for the \(x\) and \(y\) variables on one side of the equation, and the constant on the other side of the equation.

The result is referred to as the standard form of the line: \[\mathbf{Ax + By = C}.\]

Example \(\PageIndex{17}\)

Using the point-slope formula, find the standard form of an equation of the line that passes through the point (2, 3) and has slope \(-3/5\).

Solution: Substituting the point (2, 3) and \(m= - 3/5\) in the point-slope formula, we get

\[y - 3 = - 3/5(x - 2) \nonumber \]

Multiplying both sides by 5 gives us

\begin{aligned}
&5(y-3)=-3(x-2)\\
&5 y-15=-3 x+6\\
&3 x+5 y=21 \quad \text { Standard Form }
\end{aligned}

Example \(\PageIndex{18}\)

Find the standard form of the line that passes through the points (1, -2), and (4, 0).

Solution

First we find the slope: \(m = \frac{0-(-2)}{4-1} = \frac{2}{3}\)

Then, the point-slope form is: \(y - (-2) = \frac{2}{3}(x -1)\)

Multiplying both sides by 3 gives us

\begin{aligned}&3(y+2)=2(x-1) \\
&3 y+6=2 x-2\\
&-2 x+3 y=-8\\
&2 x-3 y=8 \quad \text{ Standard Form } \end{aligned}

We should always be able to convert from one form of an equation to another. For example, if we are given a line in the slope-intercept form, we should be able to express it in the standard form, and vice versa.

Example \(\PageIndex{19}\)

Write the equation \(y = -\frac{2}{3}x + 3\) in the standard form.

Solution

Multiplying both sides of the equation by 3, we get

\begin{aligned}
&3y = -2x + 9 \\
&2x + 3y = 9 \quad \text { Standard Form }
\end{aligned}

Example \(\PageIndex{20}\)

Write the equation \(3x - 4y = 10\) in the slope-intercept form.

Solution

Solving for \(y\), we get

\begin{aligned}
&-4y = -3x + 10 \\
&y = \frac{3}{4}x - \frac{5}{2} \quad \text { Standard Form }
\end{aligned}

Finally, we learn a very quick and easy way to write an equation of a line in the standard form. But first we must learn to find the slope of a line in the standard form by inspection.

By solving for \(y\), it can easily be shown that the slope of the line \(Ax + By = C\) is \(-A/B\).
The reader should verify this.

Example \(\PageIndex{21}\)

Find the slope of the following lines, by inspection.

1. \(3x-5y=10\)
2. \(2x+7y=20\)
3. \(4x-3y=8\)

Solution

1. \(A=3\), \(B=-5\), therefore, \(m=\frac{-3}{-5}=\frac{3}{5}\)
2. \(A=2\), \(B=7\), therefore, \(m=\frac{-2}{7}=-\frac{2}{7}\)
3. \(m=\frac{-4}{-3}=\frac{4}{3}\)

Now that we know how to find the slope of a line in the standard form by inspection, our job in finding the equation of a line is going to be easy.

Example \(\PageIndex{22}\)

Find an equation of the line that passes through (2, 3) and has slope - 4/5.

Solution

Since the slope of the line is - 4/5, we know that the left side of the equation is \(4x + 5y\), and the partial equation is going to be

\[4x + 5y = c \nonumber\]

Of course, \(c\) can easily be found by substituting for \(x\) and \(y\).

\begin{aligned}
&4(2)+5(3)=c\\
&23=c
\end{aligned}

The desired equation is

\[4x + 5y = 23. \nonumber\]

If you use this method often enough, you can do these problems very quickly.

An Application Problem

Now that we have learned how to write the equation of a line, we get to apply these ideas in a variety of real-life situations.

Read the problem carefully. Highlight important information. Keep track of which values correspond to the independent variable (x) and which correspond to the dependent variable (y).

Example \(\PageIndex{1}\)

A taxi service charges $0.50 per mile plus a $5 flat fee. What will be the cost of traveling 20 miles? What will be cost of traveling \(x\) miles?

Solution

\(x\) = distance traveled, in miles and \(y\) = cost in dollars

The cost of traveling 20 miles is

\[y = (0.50)(20) + 5 = 10 + 5 = 15 \nonumber\]

The cost of traveling \(x\) miles is

\[y = (0.50)(x) + 5 = 0.50x + 5 \nonumber\]

In this problem, $0.50 per mile is referred to as the variable cost, and the flat charge $5 as the fixed cost. Now if we look at our cost equation \(y = .50x + 5\), we can see that the variable cost corresponds to the slope and the fixed cost to the \(y\)-intercept.

We summarize the forms for the equation of a line below:

Slope Intercept form: \(\mathbf{y = mx + b}\),
where \(m\) = slope, \(b\) = \(y\)-intercept

Point Slope form: \(\mathbf{y - y_1 = m(x - x_1)}\),
where \(m\) = slope, \((x_1,y_1)\) is a point on the line

Standard form: \(\mathbf{Ax + By = C}\)

Horizontal Line: \(\mathbf{y = b}\)
where \(b\) = \(y\)-intercept

Vertical Line: \(\mathbf{x = a}\)
where \(a\) = \(x\)-intercept