12.1: The Fundamental Counting Principle

A tree diagram is a useful tool for visualizing systematic counting.

Example 1

Let’s say that a person walks into a restaurant for a three course dinner. There are four different salads, three different entrees, and two different desserts to choose from. Assuming the person wants to eat a salad, an entrée and a desert, how many different meals are possible?

Solution

Figure \(\PageIndex{1}\): Tree Diagram for Three-Course Dinner

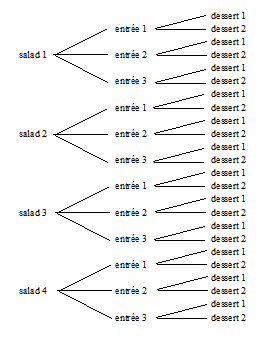
Looking at the tree diagram we can see that the total number of meals is 24. The first meal is salad 1, entrée 1, and dessert 1. The 24th meal is salad 4, entrée 3, dessert 2.

The Three Course Dinner example is easier to count the possible meals by using The Fundamental Counting Principle

The Fundamental Counting Principle

If there are \(n_1\) ways to of choosing the first item, \(n_2\) ways of choosing the second item after the first item is chosen, \(n_3\) ways of choosing the third item after the first two have been chosen, and so on until there are \(n_k\) ways of choosing the last item after the earlier choices, then the total number of choices overall is given by

\[n_1 \times n_2 \times n_3 \times n_4 \times n_5 ... \times n_k. \label{Multiplication Principle}\]

Example 1

Let’s look at the number of ways that four people can line up. We can choose any of the four people to be first. Then there are three people who can be second and two people who can be third. At this point there is only one person left to be last. Using the multiplication principle there are

\[4 \times 3 \times 2 \times 1 = 24\, \text{ways} \nonumber\]

for four people to line up.

This type of calculation occurs frequently in counting problems so we have some notation to simplify the problem.

Factorial

The factorial of \(n\), read “n factorial” is

\[n! = n(n-1)(n-2)(n-3)...(2)(1).\]

By this definition, \(0! = 1.\)

Example 2

\[\begin{align*} 5! &= 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 120 \\[5pt] 8! &= 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 40,320 \end{align*}\]

Factorials get very large very fast.

\[20! = 2.43 \times 10^{18} \nonumber\]

and

\[40! = 8.16 \times 10^{47}. \nonumber\]

70! is larger than most calculators can handle.

The fundamental counting principle may seem like a very simple idea but it is very powerful. Many complex counting problems can be solved using the fundamental counting principle.

Example 3

Some license plates in Arizona consist of three digits followed by three letters. How many license plates of this type are possible if:

1. There are 10 digits (0, 1, 2, 3, …, 9) and 26 letters. \[\underbrace{(10 \cdot 10 \cdot 10) \cdot (26 \cdot 26 \cdot 26)}_{\text{digits}}=17,576,000\, \text{license plates } \nonumber\]
2. letters can be repeated but digits cannot? \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8}) \cdot(26 \cdot 26 \cdot 26)}_{\text {letters}}=12,654,720\, \text{license plates} \nonumber\]
3. the first digit cannot be zero and both digits and letters can be repeated? \[\underbrace{(\underline{9} \cdot \underline{10} \cdot \underline{10})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot 26 \cdot 26)}_{\text{letters}}=15,818,400\, \text{license plates} \nonumber\]
4. neither digits nor numbers can be repeated. \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot \underline{25} \cdot \underline{24})}_{\text{letters}}=11,232,000 \, \text{license plates} \nonumber\]