1.9: The Real Numbers
- Last updated
- Save as PDF
- Page ID
- 18928
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Simplify expressions with square roots
- Identify integers, rational numbers, irrational numbers, and real numbers
- Locate fractions on the number line
- Locate decimals on the number line
Note
A more thorough introduction to the topics covered in this section can be found in the Prealgebra chapters, Decimals and Properties of Real Numbers.
Simplify Expressions with Square Roots
Remember that when a number \(n\) is multiplied by itself, we write \(n^{2}\) and read it “\(n\) squared.” The result is called the square of \(n\). For example,
\[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]
Similarly, 121 is the square of 11, because \(11^{2}\) is 121.
SQUARE OF A NUMBER
If \(n^{2}=m\), then \(m\) is the square of \(n\).
Note
Doing the Manipulative Mathematics activity “Square Numbers” will help you develop a better understanding of perfect square numbers.
Complete the following table to show the squares of the counting numbers 1 through 15.

The numbers in the second row are called perfect square numbers. It will be helpful to learn to recognize the perfect square numbers.
The squares of the counting numbers are positive numbers. What about the squares of negative numbers? We know that when the signs of two numbers are the same, their product is positive. So the square of any negative number is also positive.
\[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]
Did you notice that these squares are the same as the squares of the positive numbers?
Sometimes we will need to look at the relationship between numbers and their squares in reverse. Because \(10^{2}=100\), we say 100 is the square of 10. We also say that 10 is a square root of 100. A number whose square is mm is called a square root of \(m\).
SQUARE ROOT OF A NUMBER
If \(n^{2}=m\), then \(n\) is a square root of \(m\).
Notice \((−10)^{2}=100\) also, so \(−10\) is also a square root of \(100\). Therefore, both \(10\) and \(−10\) are square roots of \(100\).
So, every positive number has two square roots—one positive and one negative. What if we only wanted the positive square root of a positive number? The radical sign, \(\sqrt{m}\), denotes the positive square root. The positive square root is called the principal square root. When we use the radical sign that always means we want the principal square root.
We also use the radical sign for the square root of zero. Because \(0^{2}=0, \sqrt{0}=0\). Notice that zero has only one square root.
SQUARE ROOT NOTATION
\(\sqrt{m}\) is read “the square root of \(m\)”
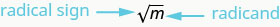
If \(m = n^{2}\), then \(\sqrt{m} = n\), for \(n\geq 0\).
The square root of \(m\), \(\sqrt{m}\), is the positive number whose square is \(m\).
Since 10 is the principal square root of 100, we write \(\sqrt{100}=10\). You may want to complete the following table to help you recognize square roots.

Exercise \(\PageIndex{1}\)
Simplify:
- \(\sqrt{25}\)
- \(\sqrt{121}\)
- Answer
-
- \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
- \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
Exercise \(\PageIndex{2}\)
Simplify:
- \(\sqrt{36}\)
- \(\sqrt{169}\)
- Answer
-
- 6
- 13
Exercise \(\PageIndex{3}\)
Simplify:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Answer
-
- 4
- 14
We know that every positive number has two square roots and the radical sign indicates the positive one. We write \(\sqrt{100)=10\). If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, \(-\sqrt{100)=-10\). We read \(-\sqrt{100)\) as “the opposite of the square root of 10.”
Exercise \(\PageIndex{4}\)
Simplify:
- \(-\sqrt{9}\)
- \(-\sqrt{144}\)
- Answer
-
- \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
- \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
Exercise \(\PageIndex{5}\)
Simplify:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Answer
-
- −2
- −15
Exercise \(\PageIndex{6}\)
Simplify:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Answer
-
- −9
- −10
Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers
We have already described numbers as counting numbers, whole numbers, and integers. What is the difference between these types of numbers?
\[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]
What type of numbers would we get if we started with all the integers and then included all the fractions? The numbers we would have form the set of rational numbers. A rational number is a number that can be written as a ratio of two integers.
RATIONAL NUMBER
A rational number is a number of the form \(\dfrac{p}{q}\), where p and q are integers and \(q \neq 0\)
A rational number can be written as the ratio of two integers.
All signed fractions, such as \(\dfrac{4}{5}\), \(-\dfrac{7}{8}\), \(\dfrac{13}{4}\), \(-\dfrac{20}{3}\) are rational numbers. Each numerator and each denominator is an integer.
Are integers rational numbers? To decide if an integer is a rational number, we try to write it as a ratio of two integers. Each integer can be written as a ratio of integers in many ways. For example, 3 is equivalent to \(\dfrac{3}{1}\), \(-\dfrac{6}{2}\), \(\dfrac{9}{3}\), \(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)
An easy way to write an integer as a ratio of integers is to write it as a fraction with denominator one.
\[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]
Since any integer can be written as the ratio of two integers, all integers are rational numbers! Remember that the counting numbers and the whole numbers are also integers, and so they, too, are rational.
What about decimals? Are they rational? Let’s look at a few to see if we can write each of them as the ratio of two integers.
We’ve already seen that integers are rational numbers. The integer \(−8\) could be written as the decimal \(−8.0\). So, clearly, some decimals are rational.
Think about the decimal \(7.3\). Can we write it as a ratio of two integers? Because \(7.3\) means \(7\dfrac{3}{10}\), we can write it as an improper fraction, \(\dfrac{73}{10}\). So \(7.3\) is the ratio of the integers \(73\) and \(10\). It is a rational number.
In general, any decimal that ends after a number of digits (such as \(7.3\) or \(−1.2684\)) is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction.
Exercise \(\PageIndex{7}\)
Write as the ratio of two integers:
- −27
- 7.31
- Answer
-
- \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
- \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]
So we see that −27 and 7.31 are both rational numbers, since they can be written as the ratio of two integers.
Exercise \(\PageIndex{8}\)
Write as the ratio of two integers:
- −24
- 3.57
- Answer
-
- \(\dfrac{-24}{1}\)
- \(\dfrac{357}{100}\)
Exercise \(\PageIndex{9}\)
Write as the ratio of two integers:
- −19
- 8.41
- Answer
-
- \(\dfrac{-19}{1}\)
- \(\dfrac{841}{100}\)
We have seen that every integer is a rational number, since \(a = \dfrac{a}{1}\) for any integer, \(a\). We can also change any integer to a decimal by adding a decimal point and a zero.
\[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]
We have also seen that every fraction is a rational number. Look at the decimal form of the fractions we considered above.
\[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]
What do these examples tell us?
Every rational number can be written both as a ratio of integers, (\(\dfrac{p}{q}\), where p and q are integers and \(q\neq 0\)),, and as a decimal that either stops or repeats.
Here are the numbers we looked at above expressed as a ratio of integers and as a decimal:
| Fractions | Integers | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | \(\frac{4}{5}\) | \(\frac{7}{8}\) | \(\frac{13}{4}\) | \(-\frac{20}{3}\) | −2 | −1 | 0 | 1 | 2 | 3 |
| Ratio of Integers | \(\frac{4}{5}\) | \(\frac{7}{8}\) | \(\frac{13}{4}\) | \(-\frac{20}{3}\) | \(-\frac{2}{1}\) | \(-\frac{1}{1}\) | \(\frac{0}{1}\) | \(\frac{1}{1}\) | \(\frac{2}{1}\) | \(\frac{3}{1}\) |
| Decimal Form | 0.8 | −0.875 | 3.25 | \(−6.\overline{6}\) | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 |
RATIONAL NUMBER
A rational number is a number of the form \(\frac{p}{q}\), where p and q are integers and \(q\neq 0\)
Its decimal form stops or repeats.
Are there any decimals that do not stop or repeat? Yes!
The number \(\pi\) (the Greek letter pi, pronounced “pie”), which is very important in describing circles, has a decimal form that does not stop or repeat.
\[\pi =3.141592654\ldots\]
We can even create a decimal pattern that does not stop or repeat, such as
\[2.01001000100001\ldots\]
Numbers whose decimal form does not stop or repeat cannot be written as a fraction of integers. We call these numbers irrational.
IRRATIONAL NUMBER
An irrational number is a number that cannot be written as the ratio of two integers.
Its decimal form does not stop and does not repeat.
Let’s summarize a method we can use to determine whether a number is rational or irrational.
RATIONAL OR IRRATIONAL?
If the decimal form of a number
- repeats or stops, the number is rational.
- does not repeat and does not stop, the number is irrational.
Exercise \(\PageIndex{10}\)
Given the numbers \(0.58\overline{3}, 0.47, 3.605551275\ldots\) list the
- rational numbers
- irrational numbers.
- Answer
-
- \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
- \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
Exercise \(\PageIndex{11}\)
For the given numbers list the
- rational numbers
- irrational numbers: \(0.29, 0.81\overline{6}, 2.515115111….\)
- Answer
-
- \(0.29, 0.81\overline{6}\)
- \(2.515115111….\)
Exercise \(\PageIndex{12}\)
For the given numbers list the
- rational numbers
- irrational numbers: \(2.6\overline{3}, 0.125, 0.418302…\)
- Answer
-
- \(2.6\overline{3}, 0.125\)
- \(0.418302…\)
Exercise \(\PageIndex{13}\)
For each number given, identify whether it is rational or irrational:
- \(\sqrt{36}\)
- \(\sqrt{44}\)
- Answer
-
- Recognize that 36 is a perfect square, since \(6^{2} = 36\). So \(\sqrt{36} = 6\), therefore \(\sqrt{36}\) is rational.
- Remember that \(6^{2} = 36\) and \(7^{2} = 49\), so \(44\) is not a perfect square. Therefore, the decimal form of \(\sqrt{44}\) will never repeat and never stop, so \(\sqrt{44}\) is irrational.
Exercise \(\PageIndex{14}\)
For each number given, identify whether it is rational or irrational:
- \(\sqrt{81}\)
- \(\sqrt{17}\)
- Answer
-
- rational
- irrational
Exercise \(\PageIndex{15}\)
For each number given, identify whether it is rational or irrational:
- \(\sqrt{116}\)
- \(\sqrt{121}\)
- Answer
-
- irrational
- rational
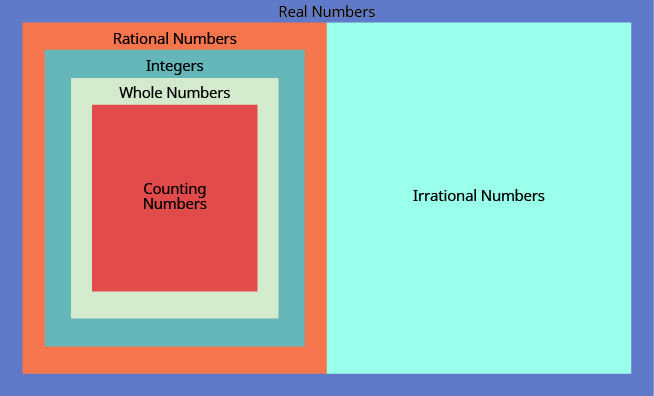
We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. The irrational numbers are numbers whose decimal form does not stop and does not repeat. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.
REAL NUMBER
A real number is a number that is either rational or irrational.
All the numbers we use in elementary algebra are real numbers. Figure \(\PageIndex{3}\) illustrates how the number sets we’ve discussed in this section fit together.
Can we simplify \(\sqrt{-25}\)? Is there a number whose square is \(−25\)?
\[(\quad)^{2}=−25?\]
None of the numbers that we have dealt with so far has a square that is \(−25\). Why? Any positive number squared is positive. Any negative number squared is positive. So we say there is no real number equal to \(\sqrt{-25}\).
The square root of a negative number is not a real number.
Exercise \(\PageIndex{16}\)
For each number given, identify whether it is a real number or not a real number:
- \(\sqrt{-169}\)
- \(-\sqrt{64}\)
- Answer
-
- There is no real number whose square is \(−169\). Therefore, \(\sqrt{-169}\) is not a real number.
- Since the negative is in front of the radical, \(-\sqrt{64}\) is \(−8\), Since \(−8\) is a real number, \(-\sqrt{64}\) is a real number.
Exercise \(\PageIndex{17}\)
For each number given, identify whether it is a real number or not a real number:
- \(\sqrt{-196}\)
- \(-\sqrt{81}\)
- Answer
-
- not a real number
- real number
Exercise \(\PageIndex{18}\)
For each number given, identify whether it is a real number or not a real number:
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- Answer
-
- real number
- not a real number
Exercise \(\PageIndex{19}\)
Given the numbers \(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), list the
- whole numbers
- integers
- rational numbers
- irrational numbers
- real numbers
- Answer
-
- Remember, the whole numbers are 0, 1, 2, 3, … and 8 is the only whole number given.
- The integers are the whole numbers, their opposites, and 0. So the whole number 8 is an integer, and −7 is the opposite of a whole number so it is an integer, too. Also, notice that 64 is the square of 8 so \(-\sqrt{64} = -8\). So the integers are \(−7, 8, \sqrt{64}\).
- Since all integers are rational, then \(-7, 8, -\sqrt{64}\) are rational. Rational numbers also include fractions and decimals that repeat or stop, so \(\frac{14}{5}\) and \(5.9\) are rational. So the list of rational numbers is \(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
- Remember that 5 is not a perfect square, so \(\sqrt{5}\) is irrational.
- All the numbers listed are real numbers.
Exercise \(\PageIndex{20}\)
For the given numbers, list the
- whole numbers
- integers
- rational numbers
- irrational numbers
- real numbers: \(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
- Answer
-
- \(4, \sqrt{49}\).
- \(−3, 4, \sqrt{49}\)
- \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
- \( -\sqrt{2}\)
- \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
Exercise \(\PageIndex{21}\)
For the given numbers, list the
- whole numbers
- integers
- rational numbers
- irrational numbers
- real numbers: \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
- Answer
-
- \(6, \sqrt{121}\).
- \(−\sqrt{25}, −1, 6, \sqrt{121}\)
- \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
- \(2.041975…\)
- \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
Locate Fractions on the Number Line
The last time we looked at the number line, it only had positive and negative integers on it. We now want to include fractions and decimals on it.
Note
Doing the Manipulative Mathematics activity “Number Line Part 3” will help you develop a better understanding of the location of fractions on the number line.
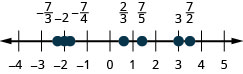
Let’s start with fractions and locate \(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) and \(\frac{8}{3}\) on the number line.
We’ll start with the whole numbers 3 and −5. because they are the easiest to plot. See Figure \(\PageIndex{4}\).
The proper fractions listed are \(\frac{1}{5}\text{ and } -\frac{4}{5}\). We know the proper fraction \(\frac{1}{5}\) has value less than one and so would be located between 0 and 1. The denominator is 5, so we divide the unit from 0 to 1 into 5 equal parts \(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). We plot \(\frac{1}{5}\). See Figure \(\PageIndex{4}\).
Similarly, \(-\frac{4}{5}\) is between 0 and −1. After dividing the unit into 5 equal parts we plot \(-\frac{4}{5}\). See Figure \(\PageIndex{4}\).
Finally, look at the improper fractions \(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). These are fractions in which the numerator is greater than the denominator. Locating these points may be easier if you change each of them to a mixed number. See Figure \(\PageIndex{4}\).
\[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]Figure \(\PageIndex{4}\) shows the number line with all the points plotted.

Exercise \(\PageIndex{22}\)
Locate and label the following on a number line: \(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) and \(\frac{7}{3}\).
- Answer
-
Locate and plot the integers, 4,−3.
Locate the proper fraction \(\frac{3}{4}\) first. The fraction \(\frac{3}{4}\) is between 0 and 1. Divide the distance between 0 and 1 into four equal parts then, we plot \(\frac{3}{4}\). Similarly plot \(-\frac{1}{4}\).
Now locate the improper fractions \(\frac{6}{5}\), \(-\frac{5}{2}\), \(\frac{7}{3}\). It is easier to plot them if we convert them to mixed numbers and then plot them as described above: \(\frac{6}{5} = 1\frac{1}{5}\), \(-\frac{5}{2} = -2\frac{1}{2}\), \(\frac{7}{3} = 2\frac{1}{3}\).

Exercise \(\PageIndex{23}\)
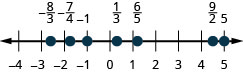
Locate and label the following on a number line: \(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) and \(-\frac{8}{3}\).
- Answer
-
Exercise \(\PageIndex{24}\)
Locate and label the following on a number line: \(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) and \(\frac{8}{3}\).
- Answer
-
In Exercise \(\PageIndex{25}\), we’ll use the inequality symbols to order fractions. In previous chapters we used the number line to order numbers.
- \(a < b\) “a is less than b” when a is to the left of b on the number line
- \(a > b\) “a is greater than b” when a is to the right of b on the number line
As we move from left to right on a number line, the values increase.
Exercise \(\PageIndex{25}\)
Order each of the following pairs of numbers, using \(<\) or \(>\). It may be helpful to refer Figure \(\PageIndex{5}\).
- \(−\frac{2}{3}\text{___}-1\)
- \(−3\frac{1}{2}\text{___}-3\)
- \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
- \(−2\text{___}-\frac{8}{3}\)

- Answer
-
Be careful when ordering negative numbers.
- \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
- \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
- \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
- \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
Exercise \(\PageIndex{26}\)
Order each of the following pairs of numbers, using \(<\) or \(>\).
- \(−\frac{1}{3}\text{___}-1\)
- \(−1\frac{1}{2}\text{___}-2\)
- \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
- \(−3\text{___}-\frac{7}{3}\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(<\)
Exercise \(\PageIndex{27}\)
Order each of the following pairs of numbers, using \(<\) or \(>\).
- \(−1\text{___}-\frac{2}{3}\)
- \(−2\frac{1}{4}\text{___}-2\)
- \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
- \(−4\text{___}-\frac{10}{3}\)
- Answer
-
- \(<\)
- \(<\)
- \(>\)
- \(<\)
Locate Decimals on the Number Line
Since decimals are forms of fractions, locating decimals on the number line is similar to locating fractions on the number line.
Exercise \(\PageIndex{28}\)
Locate 0.4 on the number line.
- Answer
-
A proper fraction has value less than one. The decimal number \(0.4\) is equivalent to \(\frac{4}{10}\), a proper fraction, so \(0.4\) is located between 0 and 1. On a number line, divide the interval between 0 and 1 into 10 equal parts. Now label the parts \(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). We write 0 as 0.0 and 1 and 1.0, so that the numbers are consistently in tenths. Finally, mark \(0.4\) on the number line. See Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\)
Exercise \(\PageIndex{29}\)
Locate on the number line: 0.6.
- Answer
-

Exercise \(\PageIndex{30}\)
Locate on the number line: 0.9.
- Answer
-

Exercise \(\PageIndex{31}\)
Locate \(−0.74\) on the number line.
- Answer
-
The decimal (−0.74\) is equivalent to \(-\frac{74}{100}\), so it is located between 0 and −1. On a number line, mark off and label the hundredths in the interval between 0 and −1. See Figure \(\PageIndex{7}\).

Figure \(\PageIndex{7}\)
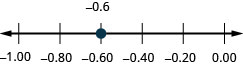
Exercise \(\PageIndex{32}\)
Locate on the number line: −0.6.
- Answer
-
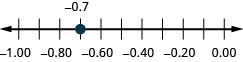
Exercise \(\PageIndex{33}\)
Locate on the number line: −0.7.
- Answer
-
Which is larger, 0.04 or 0.40? If you think of this as money, you know that $0.40 (forty cents) is greater than $0.04 (four cents). So, \(0.40 > 0.04\)
Again, we can use the number line to order numbers.
- \(a < b\) “a is less than b” when a is to the left of b on the number line
- \(a > b\) “a is greater than b” when a is to the right of b on the number line
Where are 0.04 and 0.40 located on the number line? See Figure \(\PageIndex{8}\).

We see that 0.40 is to the right of 0.04 on the number line. This is another way to demonstrate that \(0.40 > 0.04\).
How does 0.31 compare to 0.308? This doesn’t translate into money to make it easy to compare. But if we convert 0.31 and 0.308 into fractions, we can tell which is larger.
| 0.31 | 0.308 | |
| Convert to fractions. | \(\frac{31}{100}\) | \(\frac{308}{1000}\) |
| We need a common denominator to compare them. | 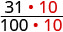 |
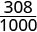 |
| \(\frac{310}{1000}\) | \(\frac{308}{1000}\) |
Because \(310 > 308\), we know that \(\frac{310}{1000} > \frac{308}{1000}\). Therefore, \(0.31 > 0.308\).
Notice what we did in converting \(0.31\) to a fraction—we started with the fraction \(\frac{31}{100}\) and ended with the equivalent fraction \(\frac{310}{1000}\).Converting \(\frac{310}{1000}\) back to a decimal gives 0.310. So 0.31 is equivalent to 0.310. Writing zeros at the end of a decimal does not change its value!
\[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]
We say 0.31 and 0.310 are equivalent decimals.
EQUIVALENT DECIMALS
Two decimals are equivalent if they convert to equivalent fractions.
We use equivalent decimals when we order decimals.
The steps we take to order decimals are summarized here.
ORDER DECIMALS.
- Write the numbers one under the other, lining up the decimal points.
- Check to see if both numbers have the same number of digits. If not, write zeros at the end of the one with fewer digits to make them match.
- Compare the numbers as if they were whole numbers.
- Order the numbers using the appropriate inequality sign.
Exercise \(\PageIndex{34}\)
Order \(0.64 \text{ ___ } 0.6\) using \(<\) or \(>\).
- Answer
-
\(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)
Exercise \(\PageIndex{35}\)
Order each of the following pairs of numbers, using \(<\) or \(>\): \(0.42 \text{ ___ } 0.4\).
- Answer
-
\(>\)
Exercise \(\PageIndex{36}\)
Order each of the following pairs of numbers, using \(<\) or \(>\): \(0.18 \text{ ___ } 0.1\).
- Answer
-
\(>\)
Exercise \(\PageIndex{37}\)
Order \(0.83 \text{ ___ } 0.803\) using \(<\) or \(>\).
- Answer
-
\(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)
Exercise \(\PageIndex{38}\)
Order each of the following pairs of numbers, using \(<\) or \(>\): \(0.76 \text{ ___ } 0.706\).
- Answer
-
\(>\)
Exercise \(\PageIndex{39}\)
Order each of the following pairs of numbers, using \(<\) or \(>\): \(0.305 \text{ ___ } 0.35\).
- Answer
-
\(<\)
When we order negative decimals, it is important to remember how to order negative integers. Recall that larger numbers are to the right on the number line. For example, because −2 lies to the right of -3 on the number line, we know that \(−2>−3\). Similarly, smaller numbers lie to the left on the number line. For example, because −9 lies to the left of −6 on the number line, we know that \(−9<−6\). See Figure \(\PageIndex{9}\).
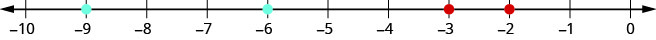
If we zoomed in on the interval between 0 and −1, as shown in Exercise \(\PageIndex{40}\), we would see in the same way that \(−0.2>−0.3\) and \(−0.9<−0.6\).
Exercise \(\PageIndex{40}\)
Use \(<\) or \(>\) to order \(−0.1\text{ ___ }−0.8\).
- Answer
-
\(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)
Exercise \(\PageIndex{41}\)
Order the following pair of numbers, using \(<\) or \(>\): \(−0.3\text{ ___ }−0.5\).
- Answer
-
\(>\)
Exercise \(\PageIndex{42}\)
Order the following pair of numbers, using \(<\) or \(>\): \(−0.6\text{ ___ }−0.7\).
- Answer
-
\(>\)
Key Concepts
- Square Root Notation
\(\sqrt{m}\) is read ‘the square root of \(m\).’ If \(m = n^{2}\), then \(\sqrt{m} = n\), for \(n \geq 0\). - Order Decimals
- Write the numbers one under the other, lining up the decimal points.
- Check to see if both numbers have the same number of digits. If not, write zeros at the end of the one with fewer digits to make them match.
- Compare the numbers as if they were whole numbers.
- Order the numbers using the appropriate inequality sign.
Practice Makes Perfect
Simplify Expressions with Square Roots
In the following exercises, simplify.


