4.2: Graph Linear Equations in Two Variables
- Last updated
- May 3, 2019
- Save as PDF
- Page ID
- 18948
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Recognize the relationship between the solutions of an equation and its graph.
- Graph a linear equation by plotting points.
- Graph vertical and horizontal lines.
Note
Before you get started, take this readiness quiz.
- Evaluate 3x+2 when x=−1.
If you missed this problem, review Exercise 1.5.34. - Solve 3x+2y=12 for y in general.
If you missed this problem, review Exercise 2.6.16.
Recognize the Relationship Between the Solutions of an Equation and its Graph
In the previous section, we found several solutions to the equation 3x+2y=6. They are listed in Table 4.2.1. So, the ordered pairs (0,3), (2,0), and (1,32) are some solutions to the equation 3x+2y=6. We can plot these solutions in the rectangular coordinate system as shown in Figure 4.2.1.
| 3x+2y=6 | ||
| x | y | (x,y) |
| 0 | 3 | (0,3) |
| 2 | 0 | (2,0) |
| 1 | 32 | (1,32) |
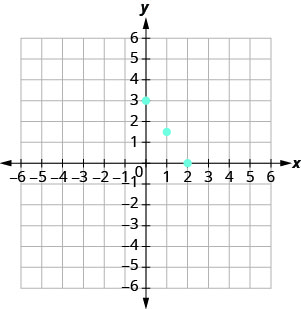
Notice how the points line up perfectly? We connect the points with a line to get the graph of the equation 3x+2y=6. See Figure 4.2.2. Notice the arrows on the ends of each side of the line. These arrows indicate the line continues.
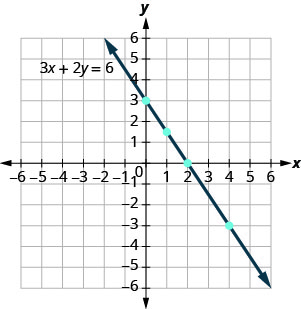
Every point on the line is a solution of the equation. Also, every solution of this equation is a point on this line. Points not on the line are not solutions.
Notice that the point whose coordinates are (−2,6) is on the line shown in Figure 4.2.3. If you substitute x=−2 and y=6 into the equation, you find that it is a solution to the equation.
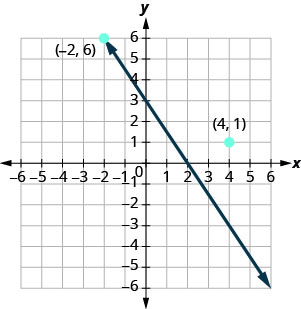
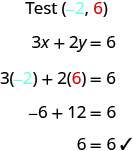
So the point (−2,6) is a solution to the equation 3x+2y=6. (The phrase “the point whose coordinates are (−2,6)” is often shortened to “the point (−2,6).”)
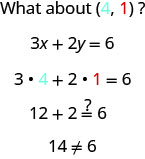
GRAPH OF A LINEAR EQUATION
The graph of a linear equation Ax+By=C is a line.- Every point on the line is a solution of the equation.
- Every solution of this equation is a point on this line.
Example 4.2.1
The graph of y=2x−3 is shown.
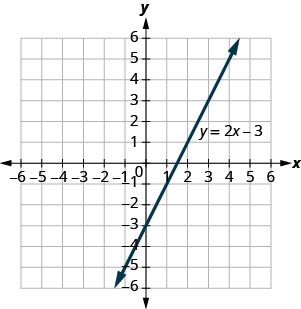
For each ordered pair, decide:
- Is the ordered pair a solution to the equation?
- Is the point on the line?
A (0,−3) B (3,3) C (2,−3) D (−1,−5)
Solution
Substitute the x- and y- values into the equation to check if the ordered pair is a solution to the equation.
1.
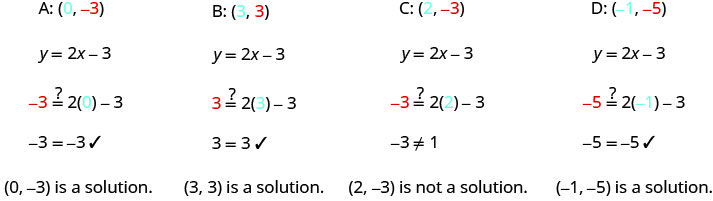
2. Plot the points A (0,−3), B (3,3), C (2,−3), and D (−1,−5).
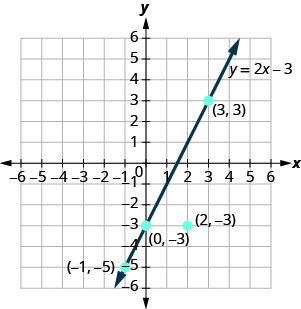
The points that are solutions to y=2x−3 are on the line, but the point that is not a solution is not on the line.
The points (0,−3), (3,3), and (−1,−5) are on the line y=2x−3, and the point (2,−3) is not on the line.
Try It 4.2.2
Use the graph of y=3x−1 to decide whether each ordered pair is:
- a solution to the equation.
- on the line.
- (0,−1)
- (2,5)
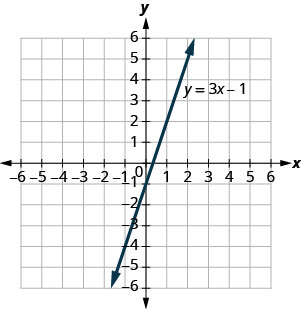
- Answer
-
- yes, yes
- yes, yes
Try It 4.2.3
Use graph of y=3x−1 to decide whether each ordered pair is:
- a solution to the equation
- on the line
- (3,−1)
- (−1,−4)
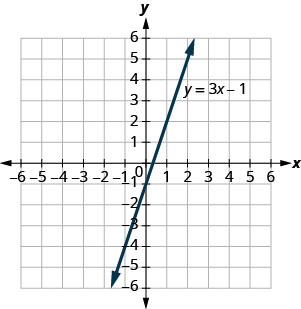
- Answer
-
- no, no
- yes, yes
Graph a Linear Equation by Plotting Points
There are several methods that can be used to graph a linear equation. The method we used to graph 3x+2y=6 is called plotting points, or the Point–Plotting Method.
Example 4.2.4: How To Graph an Equation By Plotting Points
Graph the equation y=2x+1 by plotting points.
Solution
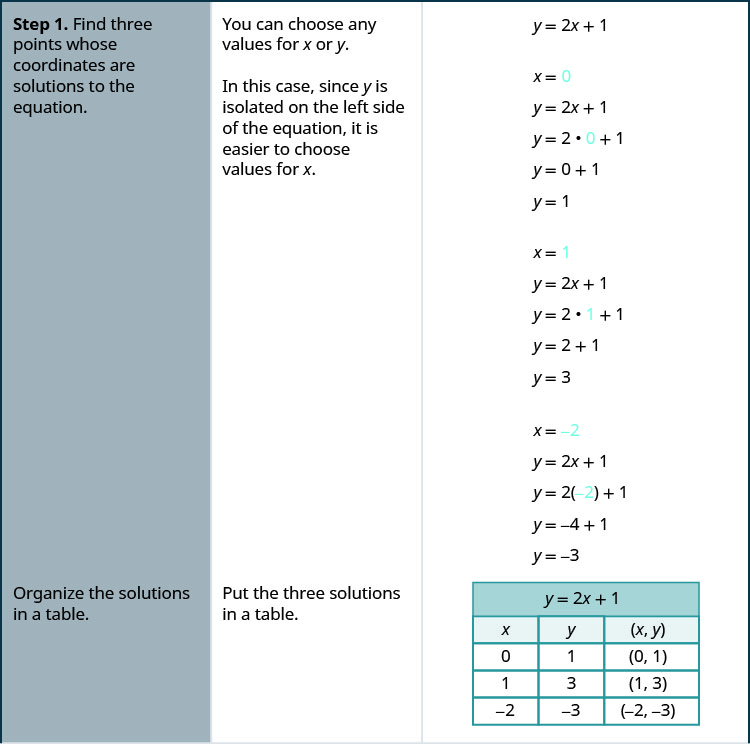
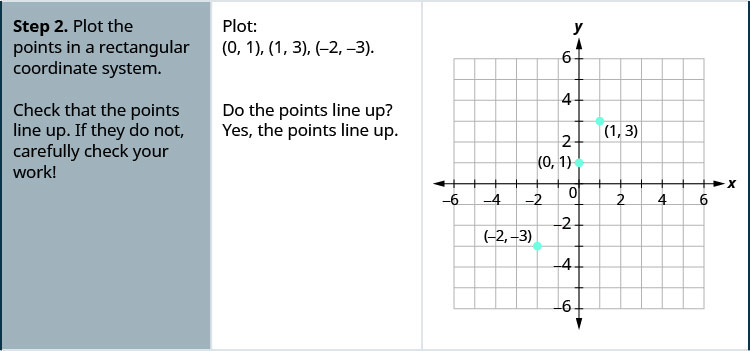
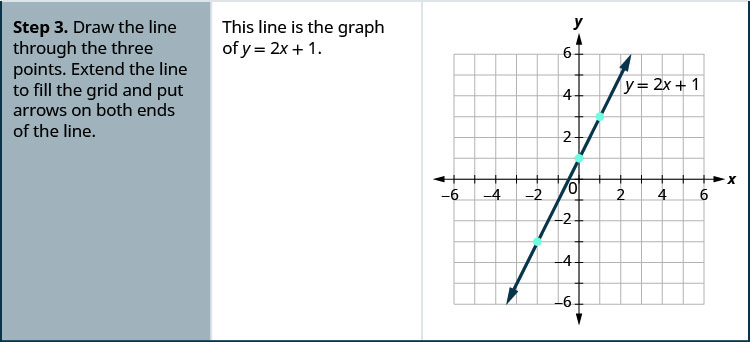
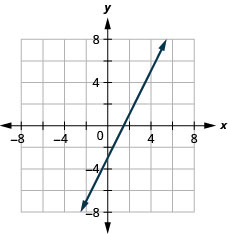
Try It 4.2.5
Graph the equation by plotting points: y=2x−3.
- Answer
-
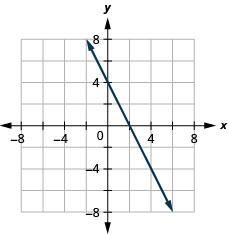
Try It 4.2.6
Graph the equation by plotting points: y=−2x+4.
- Answer
-
The steps to take when graphing a linear equation by plotting points are summarized below.
GRAPH A LINEAR EQUATION BY PLOTTING POINTS
- Find three points whose coordinates are solutions to the equation. Organize them in a table.
- Plot the points in a rectangular coordinate system. Check that the points line up. If they do not, carefully check your work.
- Draw the line through the three points. Extend the line to fill the grid and put arrows on both ends of the line.
It is true that it only takes two points to determine a line, but it is a good habit to use three points. If you only plot two points and one of them is incorrect, you can still draw a line but it will not represent the solutions to the equation. It will be the wrong line.
If you use three points, and one is incorrect, the points will not line up. This tells you something is wrong and you need to check your work. Look at the difference between part (a) and part (b) in Figure 4.2.4.

Let’s do another example. This time, we’ll show the last two steps all on one grid.
Example 4.2.7
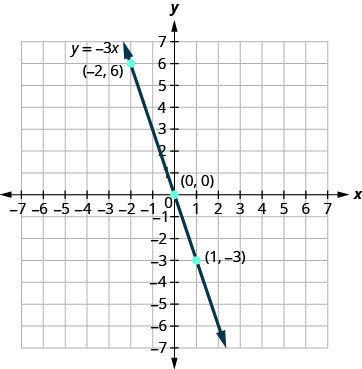
Graph the equation y=−3x.
Solution
Find three points that are solutions to the equation. Here, again, it’s easier to choose values for x. Do you see why?
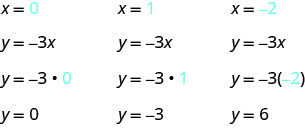
We list the points in Table 4.2.2.
| y=−3x | ||
| x | y | (x,y) |
| 0 | 0 | (0,0) |
| 1 | −3 | (1,−3) |
| −2 | 6 | (−2,6) |
Plot the points, check that they line up, and draw the line.
Try It 4.2.8
Graph the equation by plotting points: y=−4x.
- Answer
-
Try It 4.2.9
Graph the equation by plotting points: y=x.
- Answer
-
When an equation includes a fraction as the coefficient of x, we can still substitute any numbers for x. But the math is easier if we make ‘good’ choices for the values of x. This way we will avoid fraction answers, which are hard to graph precisely.
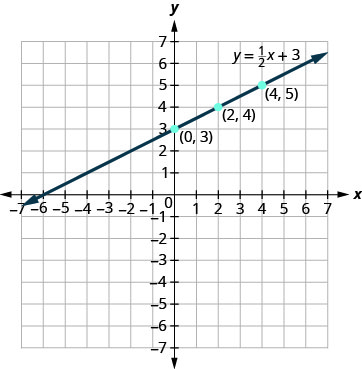
Example 4.2.10
Graph the equation y=12x+3.
Solution
Find three points that are solutions to the equation. Since this equation has the fraction 12 as a coefficient of x, we will choose values of x carefully. We will use zero as one choice and multiples of 2 for the other choices. Why are multiples of 2 a good choice for values of x?
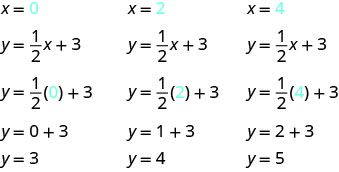
The points are shown in Table 4.2.3.
| y=12x+3 | ||
| x | y | (x,y) |
| 0 | 3 | (0,3) |
| 2 | 4 | (2,4) |
| 4 | 5 | (4,5) |
Plot the points, check that they line up, and draw the line.
Try It 4.2.11
Graph the equation y=13x−1.
- Answer
-
Try It 4.2.12
Graph the equation y=15x+2.
- Answer
-
So far, all the equations we graphed had y given in terms of x. Now we’ll graph an equation with x and y on the same side. Let’s see what happens in the equation 2x+y=3. If y=0 what is the value of x?
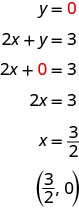
This point has a fraction for the x- coordinate and, while we could graph this point, it is hard to be precise graphing fractions. Remember in the example y=12x+3, we carefully chose values for x so as not to graph fractions at all. If we solve the equation 2x+y=3 for y, it will be easier to find three solutions to the equation.
2x+y=3y=−2x+3
The solutions for x=0, x=1, and x=−1 are shown in the Table 4.2.4. The graph is shown in Figure 4.2.5.
| 2x+y=3 | ||
| x | y | (x,y) |
| 0 | 3 | (0,3) |
| 1 | 1 | (1,1) |
| −1 | 5 | (−1,5) |
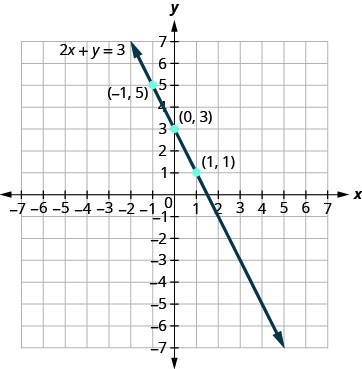
Can you locate the point (32,0) which we found by letting y=0, on the line?
Example 4.2.13
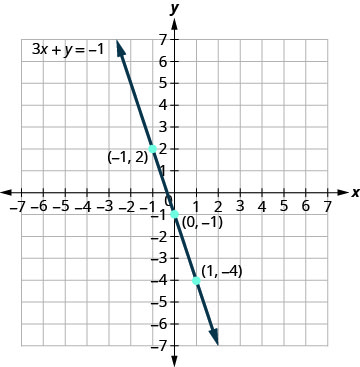
Graph the equation 3x+y=−1.
Solution
Find three points that are solutions to the equation. 3x+y=−1 First solve the equation for y.y=−3x−1
We’ll let x be 0, 1, and −1 to find 3 points. The ordered pairs are shown in Table 4.2.5. Plot the points, check that they line up, and draw the line. See Figure 4.2.6.
| 3x+y=−1 | ||
| x | y | (x,y) |
| 0 | −1 | (0,−1) |
| 1 | −4 | (1,−4) |
| −1 | 2 | (−1,2) |
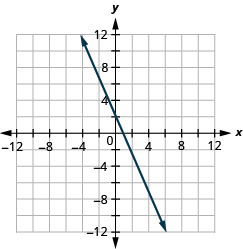
Try It 4.2.14
Graph the equation 2x+y=2.
- Answer
-
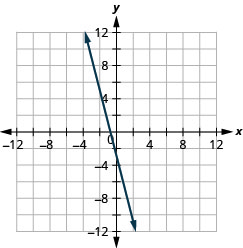
Try It 4.2.15
Graph the equation 4x+y=−3.
- Answer
-
If you can choose any three points to graph a line, how will you know if your graph matches the one shown in the answers in the book? If the points where the graphs cross the x- and y-axis are the same, the graphs match!
The equation in Example 4.2.13 was written in standard form, with both x and y on the same side. We solved that equation for y in just one step. But for other equations in standard form it is not that easy to solve for y, so we will leave them in standard form. We can still find a first point to plot by letting x=0 and solving for y. We can plot a second point by letting y=0 and then solving for x. Then we will plot a third point by using some other value for x or y.
Example 4.2.16
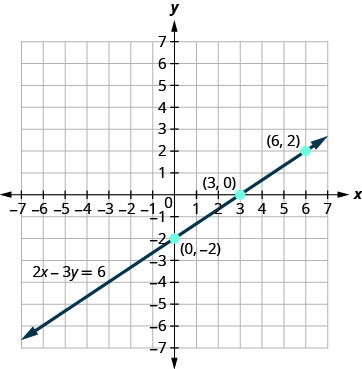
Graph the equation 2x−3y=6.
Solution
Find three points that are solutions to the 2x−3y=6 equation. 2x−3y=6 First let x=0.2(0)−3y=6 Solve for y.−3y=6y=−2 Now let y=0.2x−3(0)=6 Solve for x.2x=6x=3 We need a third point. Remember, we can2(6)−3y=6 choose any value for x or y. We’ll let x = 6.12−3y=6 Solve for y. −3y=−6y=2
We list the ordered pairs in Table 4.2.6. Plot the points, check that they line up, and draw the line. See Figure 4.2.7.
| 2x−3y=6 | ||
| x | yT | (x,y) |
| 0 | −2 | (0,−2) |
| 3 | 0 | (3,0) |
| 6 | 2 | (6,2) |
Try It 4.2.17
Graph the equation 4x+2y=8.
- Answer
-
Try It 4.2.18
Graph the equation 2x−4y=8.
- Answer
-
Graph Vertical and Horizontal Lines
Can we graph an equation with only one variable? Just x and no y, or just y without an x? How will we make a table of values to get the points to plot?
Let’s consider the equation x=−3. This equation has only one variable, x. The equation says that x is always equal to −3, so its value does not depend on y. No matter what y is, the value of x is always −3.
So to make a table of values, write −3 in for all the x values. Then choose any values for y. Since x does not depend on y, you can choose any numbers you like. But to fit the points on our coordinate graph, we’ll use 1, 2, and 3 for the y-coordinates. See Table 4.2.7
| x=−3 | ||
|---|---|---|
| x | y | (x,y) |
| −3 | 1 | (−3,1) |
| −3 | 2 | (−3,2) |
| −3 | 3 | (−3,3) |
Plot the points from Table 4.2.7 and connect them with a straight line. Notice in Figure 4.2.8 that we have graphed a vertical line.
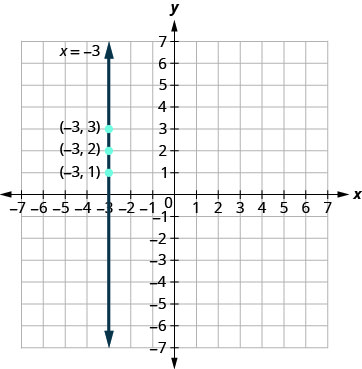
VERTICAL LINE
A vertical line is the graph of an equation of the form x=a.
The line passes through the x-axis at (a,0).
Example 4.2.19
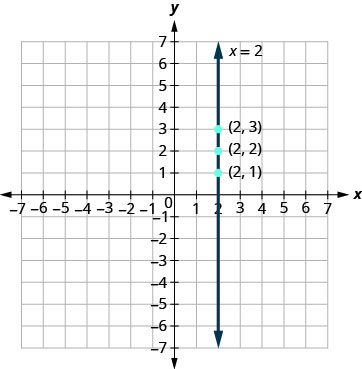
Graph the equation x=2.
Solution
The equation has only one variable, x, and x is always equal to 2. We create Table 4.2.8 where x is always 2 and then put in any values for y. The graph is a vertical line passing through the x-axis at 2. See Figure 4.2.9.
| x=2 | ||
| x | y | (x,y) |
| 2 | 1 | (2,1) |
| 2 | 2 | (2,2) |
| 2 | 3 | (2,3) |
Try It 4.2.20
Graph the equation x=5.
- Answer
-
Try It 4.2.21
Graph the equation x=−2.
- Answer
-
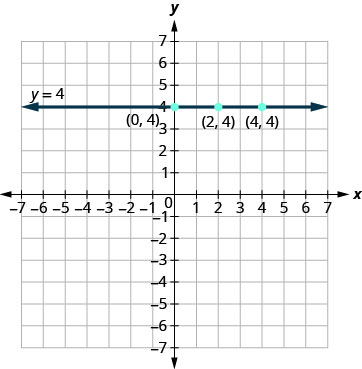
What if the equation has y but no x? Let’s graph the equation y=4. This time the y- value is a constant, so in this equation, y does not depend on x. Fill in 4 for all the y’s in Table 4.2.9 and then choose any values for x. We’ll use 0, 2, and 4 for the x-coordinates.
| y=4 | ||
| x | y | (x,y) |
| 0 | 4 | (0,4) |
| 2 | 4 | (2,4) |
| 4 | 4 | (4,4) |
The graph is a horizontal line passing through the y-axis at 4. See Figure 4.2.10.
HORIZONTAL LINE
A horizontal line is the graph of an equation of the form y=b.The line passes through the y-axis at (0,b).
Example 4.2.22
Graph the equation y=−1.
Solution
The equation y=−1 has only one variable, y. The value of y is constant. All the ordered pairs in Table 4.2.10 have the same y-coordinate. The graph is a horizontal line passing through the y-axis at −1, as shown in Figure 4.2.11.
| y=−1 | ||
| x | y | (x,y) |
| −1 | (0,−1) | |
| −1 | (3,−1) | |
| −3 | −1 | (−3,−1) |
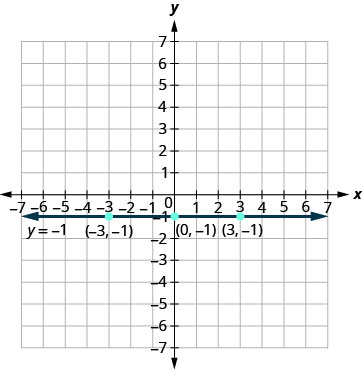
Figure 4.2.11
Try It 4.2.23
Graph the equation y=−4.
- Answer
-
Try It 4.2.24
Graph the equation y=3.
- Answer
-
The equations for vertical and horizontal lines look very similar to equations like y=4x. What is the difference between the equations y=4x and y=4?
The equation y=4x has both x and y. The value of y depends on the value of x. The y-coordinate changes according to the value of x. The equation y=4 has only one variable. The value of y is constant. The y-coordinate is always 4. It does not depend on the value of x. See Table 4.2.11.
| y=4x | y=4 | |||||
| x | y | (x,y) | x | y | (x,y) | |
| 0 | 0 | (0,0) | 0 | 4 | (0,4) | |
| 1 | 4 | (1,4) | 1 | 4 | (1,4) | |
| 2 | 8 | (2,8) | 2 | 4 | (2,4) | |
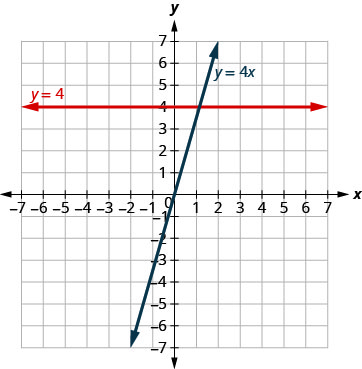
Notice, in Figure 4.2.12, the equation y=4x gives a slanted line, while y=4 gives a horizontal line.
Example 4.2.25
Graph y=−3x and y=−3 in the same rectangular coordinate system.
Solution
Notice that the first equation has the variable x, while the second does not. See Table 4.2.12. The two graphs are shown in Figure 4.2.13.
| y=−3x | y=−3 | |||||
| x | y | (x,y) | x | y | (x,y) | |
| (0,0) | −3 | (0,−3) | ||||
| −3 | (1,−3) | −3 | (1,−3) | |||
| −6 | (2,−6) | −3 | (2,−3) | |||
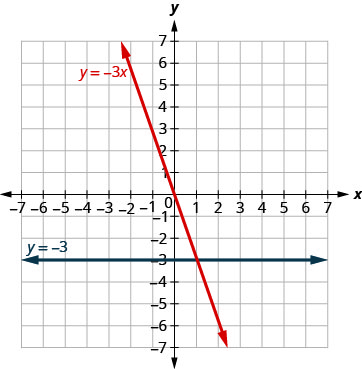
Figure 4.2.13
Try It 4.2.26
Graph y=−4x and y=−4 in the same rectangular coordinate system.
- Answer
-
Try It 4.2.27
Graph y=3 and y=3x in the same rectangular coordinate system.
- Answer
-
Key Concepts
- Graph a Linear Equation by Plotting Points
- Find three points whose coordinates are solutions to the equation. Organize them in a table.
- Plot the points in a rectangular coordinate system. Check that the points line up. If they do not, carefully check your work!
- Draw the line through the three points. Extend the line to fill the grid and put arrows on both ends of the line.
Glossary
- graph of a linear equation
- The graph of a linear equation Ax+By=C is a straight line. Every point on the line is a solution of the equation. Every solution of this equation is a point on this line.
- horizontal line
- A horizontal line is the graph of an equation of the form y=b. The line passes through the y-axis at (0,b).
- vertical line
- A vertical line is the graph of an equation of the form x=a. The line passes through the x-axis at (a,0).


