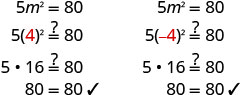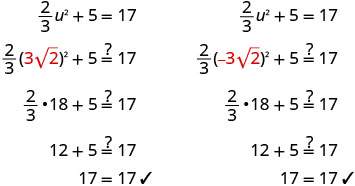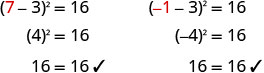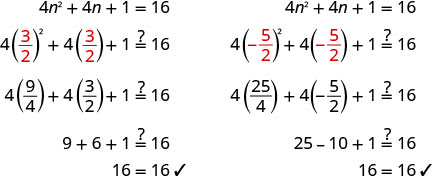Quadratic equations are equations of the form \(ax^{2} + bx + c = 0\), where \(a \neq 0\). They differ from linear equations by including a term with the variable raised to the second power. We use different methods to solve quadratic equations than linear equations, because just adding, subtracting, multiplying, and dividing terms will not isolate the variable.
We have seen that some quadratic equations can be solved by factoring. In this chapter, we will use three other methods to solve quadratic equations.
We have already solved some quadratic equations by factoring. Let’s review how we used factoring to solve the quadratic equation \(x^{2} = 9\).
\[\begin{array}{ll} {}&{x^2=9}\\ {\text{Put the equation in standard form.}}&{x^2−9=0}\\ {\text{Factor the left side.}}&{(x - 3)(x + 3) = 0}\\ {\text{Use the Zero Product Property.}}&{(x - 3) = 0, (x + 3) = 0}\\ {\text{Solve each equation.}}&{x = 3, x = -3}\\ {\text{Combine the two solutions into} \pm \text{form}}&{x=\pm 3}\\ \nonumber \end{array}\]
(The solution is read ‘\(x\) is equal to positive or negative \(3\).’)
We can easily use factoring to find the solutions of similar equations, like \(x^{2}=16\) and \(x^{2} = 25\), because \(16\) and \(25\) are perfect squares. But what happens when we have an equation like \(x^{2}=7\)? Since \(7\) is not a perfect square, we cannot solve the equation by factoring.
These equations are all of the form \(x^{2}=k\).
We defined the square root of a number in this way:
If \(n^{2} = m\), then \(n\) is a square root of \(m\).
This leads to the Square Root Property.
Definition: SQUARE ROOT PROPERTY
If \(x^{2}=k\), and \(k \geq 0\), then \(x = \sqrt{k}\) or \(x = -\sqrt{k}\).
Notice that the Square Root Property gives two solutions to an equation of the form \(x^2=k\): the principal square root of k and its opposite. We could also write the solution as \(x=\pm \sqrt{k}\)
Now, we will solve the equation \(x^{2} = 9\) again, this time using the Square Root Property.
\[\begin{array}{ll} {}&{x^{2} = 9}\\ {\text{Use the Square Root Property.}}&{x = \pm\sqrt{9}}\\ {\text{Simplify the radical.}}&{x = \pm 3}\\ {\text{Rewrite to show the two solutions.}}&{x = 3, x = −3}\\ \nonumber \end{array}\]
What happens when the constant is not a perfect square? Let’s use the Square Root Property to solve the equation \(x^2=7\).
\[\begin{array} {ll} {\text{Use the Square Root Property. }}&{x = \pm\sqrt{7}}\\ {\text{Rewrite to show two solutions.}}&{x = \sqrt{7}, x = −\sqrt{7}}\\ {\text{We cannot simplify} \sqrt{7} \text{ so we leave the answer as a radical.}}&{}\\ \nonumber \end{array}\]
Example \(\PageIndex{1}\)
Solve: \(x^{2} = 169\)
- Answer
-
\[\begin{array}{ll} {}&{x^2=169}\\ {\text{Use the Square Root Property.}}&{x=\pm\sqrt{169}}\\ {\text{Simplify the radical.}}&{x = \pm13}\\{\text{Rewrite to show two solutions.}}&{x = 13, x = −13}\\ \nonumber \end{array}\]
Example \(\PageIndex{2}\)
Solve: \(x^2=81\)
- Answer
-
x=9, x=−9
Example \(\PageIndex{3}\)
Solve: \(y^{2} = 121\)
- Answer
-
y = 11, y = −11
How to Solve a Quadratic Equation of the Form \(ax^{2} = k\) Using the Square Root Property
Example \(\PageIndex{5}\)
Solve: \(x^{2} − 50 = 0\)
- Answer
-
\(x = 5\sqrt{2}, x = −5\sqrt{2}\)
Example \(\PageIndex{6}\)
Solve: \(y^{2} − 27 = 0\)
- Answer
-
\(y = 3\sqrt{3}, x = −3\sqrt{3}\)
Definition:SOLVE A QUADRATIC EQUATION USING THE SQUARE ROOT PROPERTY.
- Isolate the quadratic term and make its coefficient one.
- Use Square Root Property.
- Simplify the radical.
- Check the solutions.
To use the Square Root Property, the coefficient of the variable term must equal 1. In the next example, we must divide both sides of the equation by 5 before using the Square Root Property.
Example \(\PageIndex{7}\)
Solve: \(5m^2=80\)
- Answer
-
| The quadratic term is isolated. |
\(5m^2=80\) |
| Divide by 5 to make its cofficient 1. |
\(\frac{5m^2}{5}=\frac{80}{5}\) |
| Simplify. |
\(m^2=16\) |
| Use the Square Root Property. |
\(m=\pm\sqrt{16}\) |
| Simplify the radical. |
\(m=\pm 4\) |
| Rewrite to show two solutions. |
m=4,m=−4 |
|
Check the solutions.
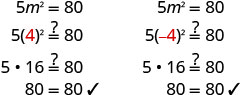
|
|
Example \(\PageIndex{8}\)
Solve: \(2x^2=98\).
- Answer
-
x=7, x=−7
Example \(\PageIndex{9}\)
Solve: \(3z^2=108\).
- Answer
-
z=6, z=−6
The Square Root Property started by stating, ‘If \(x^2=k\), and \(k\ge 0\)’. What will happen if \(k<0\)? This will be the case in the next example.
Example \(\PageIndex{10}\)
Solve: \(q^2+24=0\).
- Answer
-
\[\begin{array}{ll} {}&{q^2=24}\\ {\text{Isolate the quadratic term.}}&{q^2=−24}\\ {\text{Use the Square Root Property.}}&{q=\pm\sqrt{-24}}\\ {\text{The} \sqrt{-24} \text{is not a real number}}& {\text{There is no real solution}}\\ \nonumber \end{array}\]
Example \(\PageIndex{11}\)
Solve: \(c^2+12=0\).
- Answer
-
no real solution
Example \(\PageIndex{12}\)
Solve: \(d^2+81=0\).
- Answer
-
no real solution
Example \(\PageIndex{13}\)
Solve: \(\frac{2}{3}u^2+5=17\).
- Answer
-
| |
\(\frac{2}{3}u^2+5=17\) |
| Isolate the quadratic term. |
\(\frac{2}{3}u^2=12\)
|
| Multiply by \(\frac{3}{2}\) to make the coefficient 1. |
\(\frac{3}{2}·\frac{2}{3}u^2=\frac{3}{2}·12\) |
| Simplify. |
\(u^2=18\) |
| Use the Square Root Property. |
\(u=\pm\sqrt{18}\) |
| Simplify the radical. |
\(u=\pm\sqrt{9}\sqrt{2}\) |
| Simplify. |
\(u=\pm3\sqrt{2}\) |
| Rewrite to show two solutions. |
\(u=3\sqrt{2}\), \(u=−3\sqrt{2}\) |
|
Check.
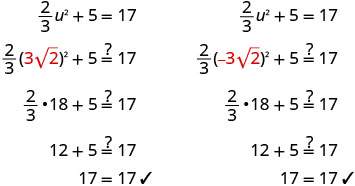
|
|
Example \(\PageIndex{14}\)
Solve: \(\frac{1}{2}x^2+4=24\)
- Answer
-
\(x=2\sqrt{10}\), \(x=−2\sqrt{10}\)
Example \(\PageIndex{15}\)
Solve: \(\frac{3}{4}y^2−3=18\).
- Answer
-
\(y=2\sqrt{7}\), \(y=−2\sqrt{7}\)
The solutions to some equations may have fractions inside the radicals. When this happens, we must rationalize the denominator.
Example \(\PageIndex{16}\)
Solve: \(2c^2−4=45\).
- Answer
-
| |
\(2c^2−4=45\) |
| Isolate the quadratic term. |
\(2c^2=49\) |
| Divide by 2 to make the coefficient 1. |
\(\frac{2c^2}{2}=\frac{49}{2}\) |
| Simplify. |
\(c^2=\frac{49}{2}\) |
| Use the Square Root Property. |
\(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) |
| Simplify the radical. |
\(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) |
| Rationalize the denominator. |
\(c=\pm\frac{\sqrt{49}\sqrt{2}}{\sqrt{2}\sqrt{2}}\) |
| Simplify. |
\(c=\pm\frac{7\sqrt{2}}{2}\) |
| Rewrite to show two solutions. |
\(c=\frac{7\sqrt{2}}{2}\), \(c=−\frac{7\sqrt{2}}{2}\) |
| Check. We leave the check for you. |
|
Example \(\PageIndex{17}\)
Solve: \(5r^2−2=34\).
- Answer
-
\(r=\frac{6\sqrt{5}}{5}\), \(r=−\frac{6\sqrt{5}}{5}\)
Example \(\PageIndex{18}\)
Solve: \(3t^2+6=70\).
- Answer
-
\(t=\frac{8\sqrt{3}}{3}\),\(t=−\frac{8\sqrt{3}}{3}\)
We can use the Square Root Property to solve an equation like \((x−3)^2=16\), too. We will treat the whole binomial, (x−3), as the quadratic term.
Example \(\PageIndex{19}\)
Solve: \((x−3)^2=16\).
- Answer
-
| |
\((x−3)^2=16\) |
| Use the Square Root Property. |
\(x−3=\pm\sqrt{16}\) |
| Simplify. |
\(x−3=\pm 4\) |
| Write as two equations. |
\(x−3=4\), \(x−3=−4\) |
| Solve. |
x=7,x=−1 |
|
Check.
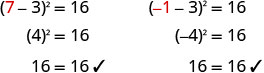
|
|
Example \(\PageIndex{20}\)
Solve: \((q+5)^2=1\).
- Answer
-
q=−6, q=−4
Example \(\PageIndex{21}\)
Solve: \((r−3)^2=25\).
- Answer
-
r=8, r=−2
Example \(\PageIndex{22}\)
Solve: \((y−7)^2=12\).
- Answer
-
| |
\((y−7)^2=12\). |
| Use the Square Root Property. |
\(y−7=\pm\sqrt{12}\) |
| Simplify the radical. |
\(y−7=\pm2\sqrt{3}\) |
| Solve for y. |
\(y=7\pm2\sqrt{3}\) |
| Rewrite to show two solutions. |
\(y=7+2\sqrt{3}\),\(y=7−2\sqrt{3}\) |
|
Check.

|
|
Example \(\PageIndex{23}\)
Solve: \((a−3)^2=18\).
- Answer
-
\(a=3+3\sqrt{2}\), \(a=3−3\sqrt{2}\)
Example \(\PageIndex{24}\)
Solve: \((b+2)^2=40\).
- Answer
-
\(b=−2+2\sqrt{10}\), \(b=−2−2\sqrt{10}\)
Example \(\PageIndex{25}\)
Solve: \((x−\frac{1}{2})^2=\frac{5}{4}\).
- Answer
-
| |
\((x−\frac{1}{2})^2=\frac{5}{4}\) |
| Use the Square Root Property. |
\((x−\frac{1}{2})=\pm\sqrt\frac{5}{4}\) |
| Rewrite the radical as a fraction of square roots. |
\((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{\sqrt{4}}\) |
| Simplify the radical. |
\((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{2}\) |
| Solve for x. |
\(x=\frac{1}{2}+\pm\frac{\sqrt{5}}{2}\) |
| Rewrite to show two solutions. |
\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}\), \(x=\frac{1}{2}−\frac{\sqrt{5}}{2}\) |
| Check. We leave the check for you |
|
Example \(\PageIndex{26}\)
Solve: \((x−\frac{1}{3})^2=\frac{5}{9}\).
- Answer
-
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}\), \(x=\frac{1}{3}−\frac{\sqrt{5}}{3}\)
Example \(\PageIndex{27}\)
Solve: \((y−\frac{3}{4})^2=\frac{7}{16}\).
- Answer
-
\(y=\frac{3}{4}+\frac{\sqrt{7}}{4}\), \(y=\frac{3}{4}−\frac{\sqrt{7}}{4}\),
We will start the solution to the next example by isolating the binomial.
Example \(\PageIndex{28}\)
Solve: \((x−2)^2+3=30\).
- Answer
-
| |
\((x−2)^2+3=30\) |
| Isolate the binomial term. |
\((x−2)^2=27\) |
| Use the Square Root Property. |
\(x−2=\pm\sqrt{27}\) |
| Simplify the radical. |
\(x−2=\pm3\sqrt{3}\) |
| Solve for x. |
\(x=2+\pm3\sqrt{3}\) |
| \(x−2=\pm3\sqrt{3}\) |
\(x=2+3\sqrt{3}\), \(x=2−3\sqrt{3}\) |
| Check. We leave the check for you |
|
Example \(\PageIndex{29}\)
Solve: \((a−5)^2+4=24\).
- Answer
-
\(a=5+2\sqrt{5}\), \(a=5−2\sqrt{5}\)
Example \(\PageIndex{30}\)
Solve: \((b−3)^2−8=24\).
- Answer
-
\(b=3+4\sqrt{2}\), \(b=3−4\sqrt{2}\)
Example \(\PageIndex{31}\)
Solve:\((3v−7)^2=−12\).
- Answer
-
| |
\((3v−7)^2=−12\) |
| Use the Square Root Property. |
\(3v−7=\pm\sqrt{−12}\) |
| The \(\sqrt{−12}\) is not a real number. |
There is no real solution. |
Example \(\PageIndex{32}\)
Solve: \((3r+4)^2=−8\).
- Answer
-
no real solution
The left sides of the equations in the next two examples do not seem to be of the form \(a(x−h)^2\). But they are perfect square trinomials, so we will factor to put them in the form we need.
Example \(\PageIndex{33}\)
Solve: \(p^2−10p+25=18\).
- Answer
-
The left side of the equation is a perfect square trinomial. We will factor it first.
| |
\(p^2−10p+25=18\) |
| Factor the perfect square trinomial. |
\((p−5)^2=18\) |
| Use the Square Root Property. |
\(p−5=\pm\sqrt{18}\) |
| Simplify the radical. |
\(p−5=\pm3\sqrt{2}\) |
| Solve for p. |
\(p=5\pm3\sqrt{2}\) |
| Rewrite to show two solutions. |
\(p=5+3\sqrt{2}\), \(p=5−3\sqrt{2}\) |
| Check. We leave the check for you. |
|
Example \(\PageIndex{34}\)
Solve: \(x^2−6x+9=12\).
- Answer
-
\(x=3+2\sqrt{3}\), \(x=3−2\sqrt{3}\)
Example \(\PageIndex{35}\)
Solve: \(y^2+12y+36=32\).
- Answer
-
\(y=−6+4\sqrt{2}\), \(y=−6−4\sqrt{2}\)
Example \(\PageIndex{36}\)
Solve: \(4n^2+4n+1=16\).
- Answer
-
Again, we notice the left side of the equation is a perfect square trinomial. We will factor it first.
| |
\(4n^2+4n+1=16\) |
| Factor the perfect square trinomial. |
\((2n+1)^2=16\) |
| Use the Square Root Property. |
\((2n+1)=\pm\sqrt{16}\) |
| Simplify the radical. |
\((2n+1)=\pm4\) |
| Solve for n. |
\(2n=−1\pm4\) |
| Divide each side by 2. |
\(\frac{2n}{2}=\frac{−1\pm4}{2}\)
\(n=\frac{−1\pm4}{2}\)
|
| Rewrite to show two solutions. |
\(n=\frac{−1+4}{2}\), \(n=\frac{−1−4}{2}\) |
| Simplify each equation. |
\(n=\frac{3}{2}\), \(n=−\frac{5}{2}\) |
|
Check.
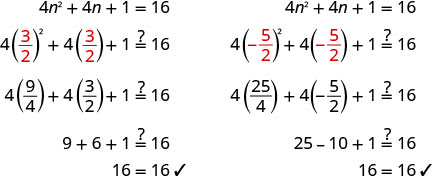
|
|
Example \(\PageIndex{37}\)
Solve: \(9m^2−12m+4=25\).
- Answer
-
\(m=\frac{7}{3}\), \(m=−1\)
Example \(\PageIndex{38}\)
Solve: \(16n^2+40n+25=4\).
- Answer
-
\(n=−\frac{3}{4}\), \(n=−\frac{7}{4}\)
Access these online resources for additional instruction and practice with solving quadratic equations:
Key Concepts
- Square Root Property
If \(x^2=k\), and \(k\ge 0\), then \(x=\sqrt{k}\) or \(x=−\sqrt{k}\).
Glossary
- quadratic equation
- A quadratic equation is an equation of the form \(ax^2+bx+c=0\) where \(a \ne 0\).
- Square Root Property
- The Square Root Property states that, if \(x^2=k\), and \(k\ge 0\), then \(x=\sqrt{k}\) or \(x=−\sqrt{k}\).