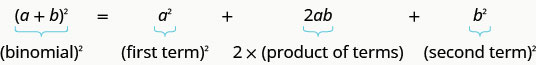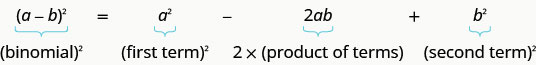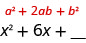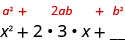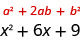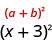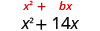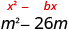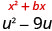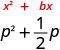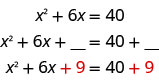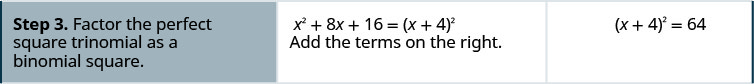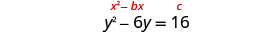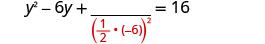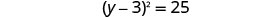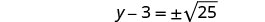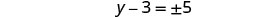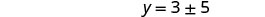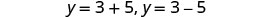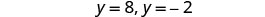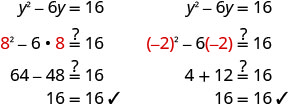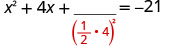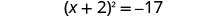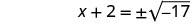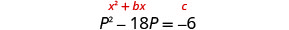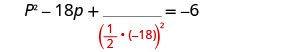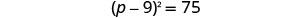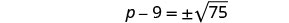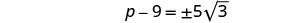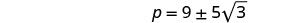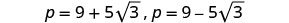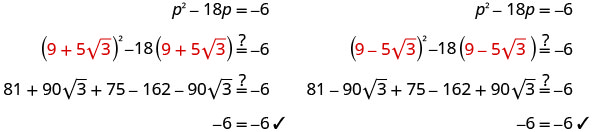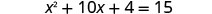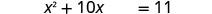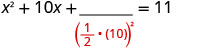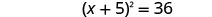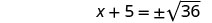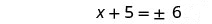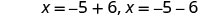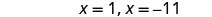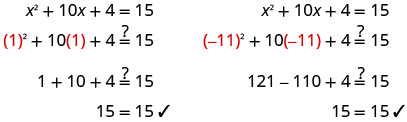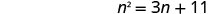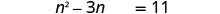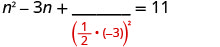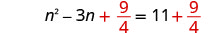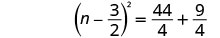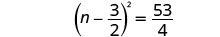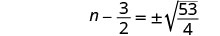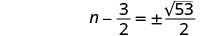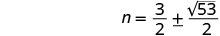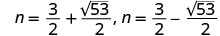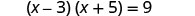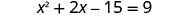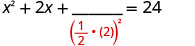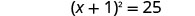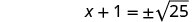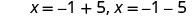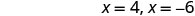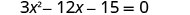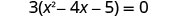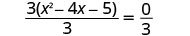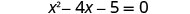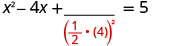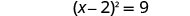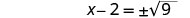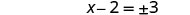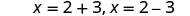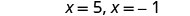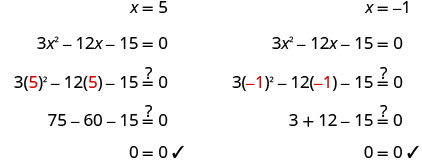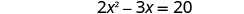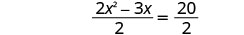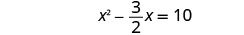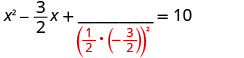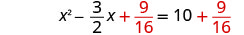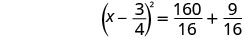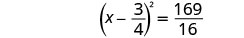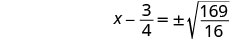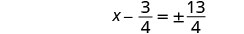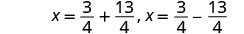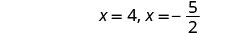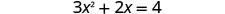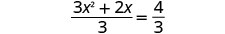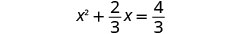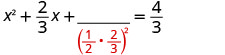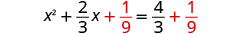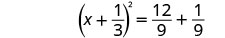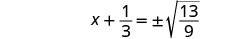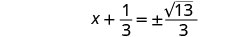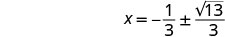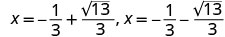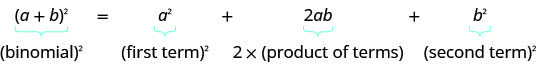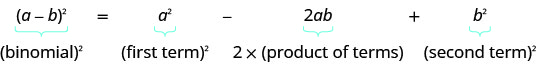Learning Objectives
By the end of this section, you will be able to:
- Complete the square of a binomial expression
- Solve quadratic equations of the form \(x^2+bx+c=0\) by completing the square
- Solve quadratic equations of the form \(ax^2+bx+c=0\) by completing the square
Note
Before you get started, take this readiness quiz. If you miss a problem, go back to the section listed and review the material.
- Simplify \((x+12)^2\).
If you missed this problem, review Example 6.4.1.
- Factor \(y^2−18y+81\).
If you missed this problem, review Exercise 7.4.1.
- Factor \(5n^2+40n+80\).
If you missed this problem, review Exercise 7.4.13.
So far, we have solved quadratic equations by factoring and using the Square Root Property. In this section, we will solve quadratic equations by a process called ‘completing the square.’
Complete The Square of a Binomial Expression
In the last section, we were able to use the Square Root Property to solve the equation \((y−7)^2=12\) because the left side was a perfect square.
\[\begin{array}{l} {(y−7)^2=12}\\ {y−7=\pm\sqrt{12}}\\ {y−7=\pm2\sqrt{3}}\\ {y=7\pm2\sqrt{3}}\\ \nonumber \end{array}\]
We also solved an equation in which the left side was a perfect square trinomial, but we had to rewrite it the form \((x−k)^2\) in order to use the square root property.
\[\begin{array}{l} {x^2−10x+25=18}\\ {(x−5)^2=18}\\ \nonumber \end{array}\]
What happens if the variable is not part of a perfect square? Can we use algebra to make a perfect square?
Let’s study the binomial square pattern we have used many times. We will look at two examples.
\[\begin{array}{ll} {(x+9)^2}&{(y−7)^2}\\ {(x+9)(x+9)}&{(y−7)(y−7)}\\ {x^2+9x+9x+81}&{y^2−7y−7y+49}\\ {x^2+18x+81}&{y^2−14y+49}\\ \nonumber \end{array}\]
Definition: BINOMIAL SQUARES PATTERN
If a,b are real numbers,
\((a+b)^2=a^2+2ab+b^2\)
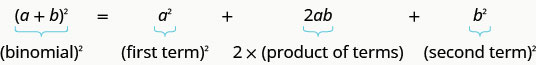
\((a−b)^2=a^2−2ab+b^2\)
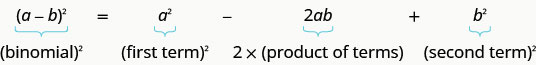
We can use this pattern to “make” a perfect square.
We will start with the expression \(x^2+6x\). Since there is a plus sign between the two terms, we will use the \((a+b)^2\) pattern.
\(a^2+2ab+b^2=(a+b)^2\)
Notice that the first term of \(x^2+6x\) is a square, \(x^2\).
We now know \(a=x\).
What number can we add to \(x^2+6x\) to make a perfect square trinomial?
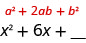
The middle term of the Binomial Squares Pattern, 2ab, is twice the product of the two terms of the binomial. This means twice the product of x and some number is 6x. So, two times some number must be six. The number we need is \(\frac{1}{2}·6=3\). The second term in the binomial, b, must be 3.
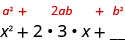
We now know \(b=3\).
Now, we just square the second term of the binomial to get the last term of the perfect square trinomial, so we square three to get the last term, nine.
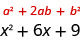
We can now factor to
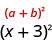
So, we found that adding nine to \(x^2+6x\) ‘completes the square,’ and we write it as \((x+3)^2\).
Definition: COMPLETE A SQUARE
To complete the square of \(x^2+bx\):
- Identify b, the coefficient of x.
- Find \((\frac{1}{2}b)^2\), the number to complete the square.
- Add the\( (\frac{1}{2}b)^2\) to \(x^2+bx\).
Example \(\PageIndex{1}\)
Complete the square to make a perfect square trinomial. Then, write the result as a binomial square.
\(x^2+14x\)
- Answer
-
| The coefficient of x is 14. |
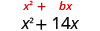 |
|
Find \((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅14)^2\)
\((7)^2\)
49
|
|
| Add 49 to the binomial to complete the square. |
\(x^2+14x+49\) |
| Rewrite as a binomial square. |
\((x+7)^2\) |
Example \(\PageIndex{2}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(y^2+12y\)
- Answer
-
\((y+6)^2\)
Example \(\PageIndex{3}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(z^2+8z\)
- Answer
-
\((z+4)^2\)
Example \(\PageIndex{4}\)
Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared. \(m^2−26m\)
- Answer
-
| |
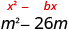 |
|
Find \((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅(−26))^2\)
\((−13)^2\)
169
|
|
| Add 169 to the binomial to complete the square. |
\(m^2−26m+169\) |
| Rewrite as a binomial square. |
\((m−13)^2\) |
Example \(\PageIndex{5}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(a^2−20a\)
- Answer
-
\((a−10)^2\)
Example \(\PageIndex{6}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(b^2−4b\)
- Answer
-
\((b−2)^2\)
Example \(\PageIndex{7}\)
Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.
\(u^2−9u\)
- Answer
-
| The coefficient of u is −9. |
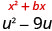 |
|
Find \((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅(−9))^2\)
\((−\frac{9}{2})^2\)
\(\frac{81}{4}\)
|
|
| Add \(\frac{81}{4}\) to the binomial to complete the square. |
\(u^2−9u+\frac{81}{4}\) |
| Rewrite as a binomial square. |
\((u−\frac{9}{2})^2\) |
Example \(\PageIndex{8}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(m^2−5m\)
- Answer
-
\((m−\frac{5}{2})^2\)
Example \(\PageIndex{9}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(n^2+13n\)
- Answer
-
\((n+\frac{13}{2})^2\)
Example \(\PageIndex{10}\)
Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.
\(p^2+12p\)
- Answer
-
| The coefficient of p is \(\frac{1}{2}\) |
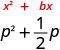 |
|
Find \((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅\frac{1}{2})^2\)
\((\frac{1}{4})^2\)
\(\frac{1}{16}\)
|
|
| Add \(\frac{1}{16}\) to the binomial to complete the square. |
\(p^2+\frac{1}{2}p+\frac{1}{16}\) |
| Rewrite as a binomial square. |
\((p+\frac{1}{4})^2\) |
Example \(\PageIndex{11}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(p^2+\frac{1}{4}p\)
- Answer
-
\((p+\frac{1}{8})^2\)
Example \(\PageIndex{12}\)
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
\(q^2−\frac{2}{3}q\)
- Answer
-
\((q−\frac{1}{3})^2\)
In solving equations, we must always do the same thing to both sides of the equation. This is true, of course, when we solve a quadratic equation by completing the square, too. When we add a term to one side of the equation to make a perfect square trinomial, we must also add the same term to the other side of the equation.
For example, if we start with the equation \(x^2+6x=40\) and we want to complete the square on the left, we will add nine to both sides of the equation.
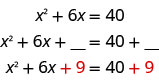
Then, we factor on the left and simplify on the right.
\((x+3)^2=49\)
Now the equation is in the form to solve using the Square Root Property. Completing the square is a way to transform an equation into the form we need to be able to use the Square Root Property.
How To Solve a Quadratic Equation of the Form \(x^2+bx+c=0\) by Completing the Square.
Example \(\PageIndex{14}\)
Solve \(c^2+4c=5\) by completing the square.
- Answer
-
\(c=−5\), \(c=1\)
Example \(\PageIndex{15}\)
Solve \(d^2+10d=−9\) by completing the square.
- Answer
-
\(d=−9\), \(d=−1\)
- Isolate the variable terms on one side and the constant terms on the other.
- Find \((\frac{1}{2}·b)^2\), the number to complete the square. Add it to both sides of the equation.
- Factor the perfect square trinomial as a binomial square.
- Use the Square Root Property.
- Simplify the radical and then solve the two resulting equations.
- Check the solutions.
Example \(\PageIndex{17}\)
Solve \(r^2−4r=12\) by completing the square.
- Answer
-
\(r=−2\), \(r=6\)
Example \(\PageIndex{18}\)
Solve \(t^2−10t=11\) by completing the square.
- Answer
-
\(t=−1\), \(t=11\)
Example \(\PageIndex{20}\)
Solve \(y^2−10y=−35\) by completing the square.
- Answer
-
no real solution
Example \(\PageIndex{21}\)
Solve \(z^2+8z=−19\) by completing the square.
- Answer
-
no real solution
In the previous example, there was no real solution because \((x+k)^2\) was equal to a negative number.
Example \(\PageIndex{22}\)
Solve \(p^2−18p=−6\) by completing the square.
- Answer
-
Another way to check this would be to use a calculator. Evaluate \(p^2−18p\) for both of the solutions. The answer should be −6.
Example \(\PageIndex{23}\)
Solve \(x^2−16x=−16\) by completing the square.
- Answer
-
\(x=8\pm4\sqrt{3}\)
Example \(\PageIndex{24}\)
Solve \(y^2+8y=11\) by completing the square.
- Answer
-
\(y=−4\pm3\sqrt{3}\)
We will start the next example by isolating the variable terms on the left side of the equation.
Example \(\PageIndex{25}\)
Solve \(x^2+10x+4=15\) by completing the square.
- Answer
-
Example \(\PageIndex{26}\)
Solve \(a^2+4a+9=30\) by completing the square.
- Answer
-
\(a=−7\), \(a=3\)
Example \(\PageIndex{27}\)
Solve \(b^2+8b−4=16\) by completing the square.
- Answer
-
\(b=−10\), \(b=2\)
To solve the next equation, we must first collect all the variable terms to the left side of the equation. Then, we proceed as we did in the previous examples.
Example \(\PageIndex{29}\)
Solve \(p^2=5p+9\) by completing the square.
- Answer
-
\(p=\frac{5}{2}\pm\frac{\sqrt{61}}{2}\)
Example \(\PageIndex{30}\)
Solve \(q^2=7q−3\) by completing the square.
- Answer
-
\(q=\frac{7}{2}\pm\frac{\sqrt{37}}{2}\)
Notice that the left side of the next equation is in factored form. But the right side is not zero, so we cannot use the Zero Product Property. Instead, we multiply the factors and then put the equation into the standard form to solve by completing the square.
Example \(\PageIndex{32}\)
Solve \((c−2)(c+8)=7\) by completing the square.
- Answer
-
\(c=−3\pm4\sqrt{2}\)
Example \(\PageIndex{33}\)
Solve \((d−7)(d+3)=56\) by completing the square.
- Answer
-
\(d=−7\), \(d=11\)
The process of completing the square works best when the leading coefficient is one, so the left side of the equation is of the form \(x^2+bx+c\). If the \(x^2\) term has a coefficient, we take some preliminary steps to make the coefficient equal to one.
Sometimes the coefficient can be factored from all three terms of the trinomial. This will be our strategy in the next example.
Example \(\PageIndex{34}\)
Solve \(3x^2−12x−15=0\) by completing the square.
- Answer
-
To complete the square, we need the coefficient of \(x^2\) to be one. If we factor out the coefficient of \(x^2\) as a common factor, we can continue with solving the equation by completing the square.
Example \(\PageIndex{35}\)
Solve \(2m^2+16m−8=0\) by completing the square.
- Answer
-
\(m=−4\pm2\sqrt{5}\)
Example \(\PageIndex{36}\)
Solve \(4n^2−24n−56=8\) by completing the square.
- Answer
-
\(n=−2, 8\)
To complete the square, the leading coefficient must be one. When the leading coefficient is not a factor of all the terms, we will divide both sides of the equation by the leading coefficient. This will give us a fraction for the second coefficient. We have already seen how to complete the square with fractions in this section.
Example \(\PageIndex{37}\)
Solve \(2x^2−3x=20\) by completing the square.
- Answer
-
Example \(\PageIndex{38}\)
Solve \(3r^2−2r=21\) by completing the square.
- Answer
-
\(r=−\frac{7}{3}\), \(r=3\)
Example \(\PageIndex{39}\)
Solve \(4t^2+2t=20\) by completing the square.
- Answer
-
\(t=−\frac{5}{2}\), \(t=2\)
Example \(\PageIndex{40}\)
Solve \(3x^2+2x=4\) by completing the square.
- Answer
-
Again, our first step will be to make the coefficient of \(x^2\) be one. By dividing both sides of the equation by the coefficient of \(x^2\), we can then continue with solving the equation by completing the square.
Example \(\PageIndex{41}\)
Solve \(4x^2+3x=12\) by completing the square.
- Answer
-
\(x=−\frac{3}{8}\pm\frac{\sqrt{201}}{8}\)
Example \(\PageIndex{42}\)
Solve \(5y^2+3y=10\) by completing the square.
- Answer
-
\(y=−\frac{3}{10}\pm\frac{\sqrt{209}}{10}\)
Access these online resources for additional instruction and practice with solving quadratic equations by completing the square:
Key Concepts
- Binomial Squares Pattern If a,ba,b are real numbers,
\((a+b)^2=a^2+2ab+b^2\)
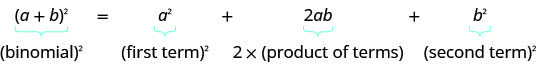
\((a−b)^2=a^2−2ab+b^2\)
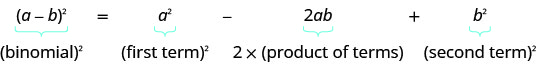
- Complete a Square
To complete the square of \(x^2+bx\):
- Identify bb, the coefficient of x.
- Find \((\frac{1}{2}b)^2\), the number to complete the square.
- Add the \((\frac{1}{2}b)^2\) to \(x^2+bx\).
Glossary
- completing the square
- Completing the square is a method used to solve quadratic equations.