1.5: Solve Inequalities

Last updated
Save as PDF

Page ID: 51443

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Describe solutions to inequalities
- Represent inequalities on a number line
- Represent inequalities using interval notation
Solve single-step inequalities
- Use the addition and multiplication properties to solve algebraic inequalities and express their solutions graphically and with interval notation
- Solve inequalities that contain absolute value
Solve multi-step inequalities
- Combine properties of inequality to isolate variables, solve algebraic inequalities, and express their solutions graphically
- Simplify and solve algebraic inequalities using the distributive property to clear parentheses and fractions

Represent inequalities on a number line

First, let’s define some important terminology. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Special symbols are used in these statements. When you read an inequality, read it from left to right—just like reading text on a page. In algebra, inequalities are used to describe large sets of solutions. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed some ways to describe very large lists in succinct ways.

The first way you are probably familiar with—the basic inequality. For example:

${x}\lt{9}$ or try to list all the possible numbers that are less than 9? (hopefully, your answer is no)
$-5$.

Note how placing the variable on the left or right of the inequality sign can change whether you are looking for greater than or less than.

For example:

$x\lt5$ means all the real numbers that are less than 5, whereas;
$x\gt{5}$ note how the inequality is still pointing the same direction relative to x. This statement represents all the real numbers that are greater than 5, which is easier to interpret than 5 is less than x.

The second way is with a graph using the number line:

$A numberline. It is a long horizontal line with evenly spaced points, the middle of which is zero.$

And the third way is with an interval.

We will explore the second and third ways in depth in this section. Again, those three ways to write solutions to inequalities are:

an inequality
an interval
a graph

Inequality Signs

The box below shows the symbol, meaning, and an example for each inequality sign. Sometimes it’s easy to get tangled up in inequalities, just remember to read them from left to right.

Symbol	Words	Example
${2}\neq{8}$, 2 is not equal to 8.
${5}\gt{1}$, 5 is greater than 1
${2}\lt{11}$, 2 is less than 11
${4}\geq{ 4}$, 4 is greater than or equal to 4
${7}\leq{9}$, 7 is less than or equal to 9

The inequality ${y}<{x}$. The sides of any inequality can be switched as long as the inequality symbol between them is also reversed.

Graphing an Inequality

Inequalities can also be graphed on a number line. Below are three examples of inequalities and their graphs. Graphs are a very helpful way to visualize information – especially when that information represents an infinite list of numbers!

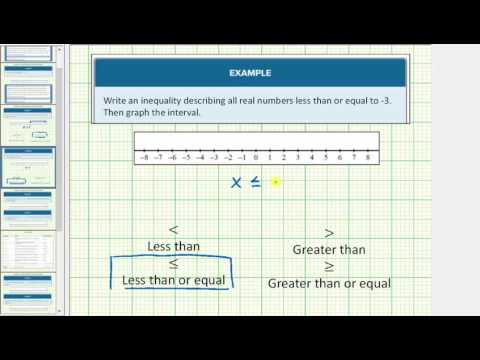
$x\leq -4$. This translates to all the real numbers on a number line that are less than or equal to 4.

$Number line. Shaded circle on negative 4. Shaded line through all numbers less than negative 4.$

${x}\geq{-3}$. This translates to all the real numbers on the number line that are greater than or equal to -3.

$Number line. Shaded circle on negative 3. Shaded line through all numbers greater than negative 3.$

Each of these graphs begins with a circle—either an open or closed (shaded) circle. This point is often called the end point of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to $\displaystyle \left(\leq\right)$. The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution.

The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. For example, notice that for the graph of $−3$, represented with a closed circle since the inequality is greater than or equal to$−3$. The arrow at the end indicates that the solutions continue infinitely.

Example

Graph the inequality $x\ge 4$
[reveal-answer q=”797241″]Show Solution[/reveal-answer]
[hidden-answer a=”797241″]

We can use a number line as shown. Because the values for x include 4, we place a solid dot on the number line at 4.

Then we draw a line that begins at $x=4$ and, as indicated by the arrowhead, continues to positive infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4.
$A number line starting at zero with the last tick mark being labeled 11. There is a dot at the number 4 and an arrow extends toward the right.$

[/hidden-answer]

This video shows an example of how to draw the graph of an inequality.

$Thumbnail for the embedded element "Graph Linear Inequalities in One Variable (Basic)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Example

Write an inequality describing all the real numbers on the number line that are less than 2, then draw the corresponding graph.
[reveal-answer q=”867890″]Show Solution[/reveal-answer]
[hidden-answer a=”867890″]

We need to start from the left and work right, so we start from negative infinity and end at $-2$.

Inequality: $x<2$

To draw the graph, place an open dot on the number line first, then draw a line extending to the left. Draw an arrow at the leftmost point of the line to indicate that it continues for infinity.

$Number line. Unshaded circle around 2 and shaded line through all numbers less than 2.$

[/hidden-answer]

The following video shows how to write an inequality mathematically when it is given in words. We will then graph it.

$Thumbnail for the embedded element "Given Interval in Words, Graph and Give Inequality"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Represent inequalities using interval notation

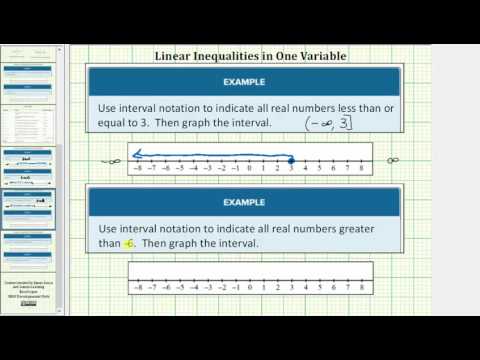
Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. With this convention, sets are built with parentheses or brackets, each having a distinct meaning. The solutions to $\left[4,\infty \right)$. This method is widely used and will be present in other math courses you may take.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are $-2$ and $-2$, but not including $\left(-1,0\right)$, all real numbers between, but not including $0$; and $1$. The table below outlines the possibilities. Remember to read inequalities from left to right, just like text.

The table below describes all the possible inequalities that can occur and how to write them using interval notation, where a and b are real numbers.

Inequality	Words	Interval Notation
$\left(a,b\right)$
$\left(a,\infty \right)$
$\left(-\infty ,b\right)$
$\left[a,\infty \right)$
$\left(-\infty ,b\right]$
$\left[a,b\right)$
$\left(a,b\right]$
$\left[a,b\right]$
$\left(-\infty ,a\right)\cup \left(b,\infty \right)$
All real numbers	All real numbers	$\left(-\infty ,\infty \right)$

Example

Describe the inequality $x\ge 4$ using interval notation
[reveal-answer q=”817362″]Show Solution[/reveal-answer]
[hidden-answer a=”817362″]

The solutions to $\left[4,\infty \right)$.

Note the use of a bracket on the left because 4 is included in the solution set.

[/hidden-answer]

In the following video we show another example of using interval notation to describe an inequality.

$Thumbnail for the embedded element "Given an Inequality, Graph and Give Interval Notation"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Example

Use interval notation to indicate all real numbers greater than or equal to $-2$.
[reveal-answer q=”961990″]Show Solution[/reveal-answer]
[hidden-answer a=”961990″]

Use a bracket on the left of $\left[-2,\infty \right)$. The bracket indicates that $-2$ to infinity.

[/hidden-answer]

In the following video we show another example of translating words into an inequality and writing it in interval notation, as well as drawing the graph.

$Thumbnail for the embedded element "Given Interval in Words, Graph and Give Interval Notation"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Think About It

In the previous examples you were given an inequality or a description of one with words and asked to draw the corresponding graph and write the interval. In this example you are given an interval and asked to write the inequality and draw the graph.

Given $\left(-\infty,10\right)$, write the associated inequality and draw the graph.

In the box below, write down whether you think it will be easier to draw the graph first or write the inequality first.

[practice-area rows=”1″][/practice-area]
[reveal-answer q=”15120″]Show Solution[/reveal-answer]

[hidden-answer a=”15120″]

We will draw the graph first.

The interval reads “all real numbers less than 10,” so we will start by placing an open dot on 10 and drawing a line to the left with an arrow indicating the solution continues to negative infinity.

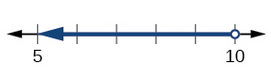
$An open circle on 10 and a line going from 10 to all numbers below 10.$

To write the inequality, we will use < since the parentheses indicate that 10 is not included. $x<10$

[/hidden-answer]

In the following video, you will see examples of how to draw a graph given an inequality in interval notation.

$Thumbnail for the embedded element "Given Interval Notation, Graph and Give Inequality"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

And finally, one last video that shows how to write inequalities using a graph, with interval notation and as an inequality.

$Thumbnail for the embedded element "Ex: Graph Basic Inequalities and Express Using Interval Notation"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Solve Single-Step Inequalities

Solve inequalities with addition and subtraction

You can solve most inequalities using inverse operations as you did for solving equations. This is because when you add or subtract the same value from both sides of an inequality, you have maintained the inequality. These properties are outlined in the box below.

Addition and Subtraction Properties of Inequality

If $a+c>b+c$.

If $a−c>b−c$.

Because inequalities have multiple possible solutions, representing the solutions graphically provides a helpful visual of the situation, as we saw in the last section. The example below shows the steps to solve and graph an inequality and express the solution using interval notation.

Example

Solve for x.

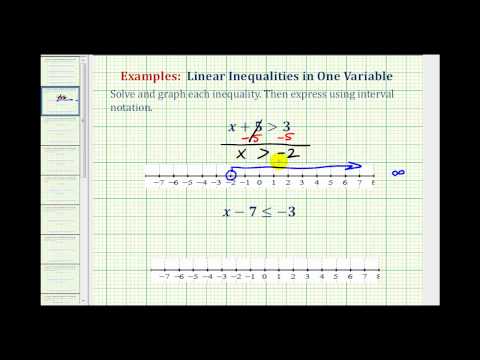
${x}+3\lt{5}$

[reveal-answer q=”952771″]Show Solution[/reveal-answer]
[hidden-answer a=”952771″]

It is helpful to think of this inequality as asking you to find all the values for x, including negative numbers, such that when you add three you will get a number less than 5.

$\displaystyle \begin{array}{l}x+3<\,\,\,\,5\\\underline{\,\,\,\,\,-3\,\,\,\,-3}\\x\,\,\,\,\,\,\,\,<\,\,\,\,2\,\,\end{array}$

Isolate the variable by subtracting 3 from both sides of the inequality.

Answer

Inequality: $x<2$

Interval: $\left(-\infty, 2\right)$

Graph: $Number line. Open circle around 2. Shaded line through all numbers less than 2.$ [/hidden-answer]

The line represents all the numbers to which you can add 3 and get a number that is less than 5. There’s a lot of numbers that solve this inequality!

Just as you can check the solution to an equation, you can check a solution to an inequality. First, you check the end point by substituting it in the related equation. Then you check to see if the inequality is correct by substituting any other solution to see if it is one of the solutions. Because there are multiple solutions, it is a good practice to check more than one of the possible solutions. This can also help you check that your graph is correct.

The example below shows how you could check that $x+3<5$.

Example

Check that $x+3<5$.

[reveal-answer q=”811564″]Show Solution[/reveal-answer]
[hidden-answer a=”811564″]

Substitute the end point 2 into the related equation, $x+3=5$.

$\begin{array}{r}x+3=5 \\ 2+3=5 \\ 5=5\end{array}$

Pick a value less than 2, such as 0, to check into the inequality. (This value will be on the shaded part of the graph.)

$Number line. Open circle around 2. Shaded line through all numbers less than 2.$

$\displaystyle \begin{array}{r}x+3<5 \\ 0+3<5 \\ 3<5\end{array}$

It checks!

$x+3<5$.[/hidden-answer]

The following examples show inequality problems that include operations with negative numbers. The graph of the solution to the inequality is also shown. Remember to check the solution. This is a good habit to build!

Example

Solve for x: $x-10\leq-12$
[reveal-answer q=”815894″]Show Solution[/reveal-answer]
[hidden-answer a=”815894″]

Isolate the variable by adding 10 to both sides of the inequality.

$\displaystyle \begin{array}{r}x-10\le -12\\\underline{\,\,\,+10\,\,\,\,\,+10}\\x\,\,\,\,\,\,\,\,\,\,\le \,\,\,-2\end{array}$

Answer

Inequality: $\left(-\infty,-2\right]$
Graph: Notice that a closed circle is used because the inequality is “less than or equal to” $−2$ because these are the values that are less than $−2$.
$Number line, closed circle on negative 2 and line drawn through all numbers less than negative 2$

[/hidden-answer]

Check the solution to $x-10\leq -12$
[reveal-answer q=”268062″]Show Solution[/reveal-answer]
[hidden-answer a=”268062″]

Substitute the end point $x-10=−12$

$\displaystyle \begin{array}{r}x-10=-12\,\,\,\\\text{Does}\,\,\,-2-10=-12?\\-12=-12\,\,\,\end{array}$

Pick a value less than $−5$, to check in the inequality. (This value will be on the shaded part of the graph.)

$\displaystyle \begin{array}{r}x-10\le -12\,\,\,\\\text{ }\,\text{ Is}\,\,-5-10\le -12?\\-15\le -12\,\,\,\\\text{It}\,\text{checks!}\end{array}$

$x-10\leq -12$

[/hidden-answer]

Example

Solve for a. $a-17>-17$
[reveal-answer q=”343031″]Show Solution[/reveal-answer]
[hidden-answer a=”343031″]

Isolate the variable by adding 17 to both sides of the inequality.

$\displaystyle \begin{array}{r}a-17>-17\\\underline{\,\,\,+17\,\,\,\,\,+17}\\a\,\,\,\,\,\,\,\,\,\,\,>\,\,\,\,\,\,0\end{array}$

Answer

Inequality: $\displaystyle a\,\,>\,0$

Interval: $\left(0,\infty\right)$ Note how we use parentheses on the left to show that the solution does not include 0.

Graph: Note the open circle to show that the solution does not include 0.

$Number line. Open circle on zero. Highlight through all numbers above zero.$

[/hidden-answer]

Check the solution to $a-17>-17$
[reveal-answer q=”653357″]Show Solution[/reveal-answer]
[hidden-answer a=”653357″]

Is $a-17>-17$?

Substitute the end point 0 into the related equation.

$\displaystyle \begin{array}{r}a-17=-17\,\,\,\\\text{Does}\,\,\,0-17=-17?\\-17=-17\,\,\,\end{array}$

Pick a value greater than 0, such as 20, to check in the inequality. (This value will be on the shaded part of the graph.)

$\displaystyle \begin{array}{r}a-17>-17\,\,\,\\\text{Is }\,\,20-17>-17?\\3>-17\,\,\,\\\\\text{It checks!}\,\,\,\,\end{array}$

$a-17>-17$

[/hidden-answer]

The previous examples showed you how to solve a one-step inequality with the variable on the left hand side. The following video provides examples of how to solve the same type of inequality.

$Thumbnail for the embedded element "Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Left Side)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

What would you do if the variable were on the right side of the inequality? In the following example, you will see how to handle this scenario.

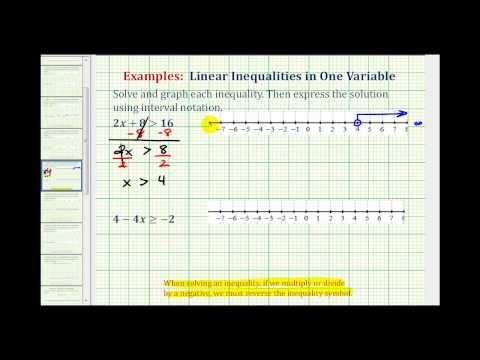
Example

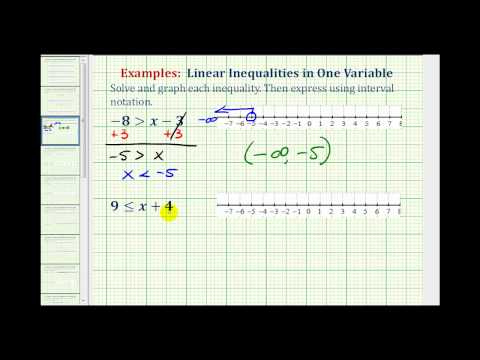
Solve for x: $4\geq{x}+5$
[reveal-answer q=”815893″]Show Solution[/reveal-answer]
[hidden-answer a=”815893″]

Isolate the variable by adding 10 to both sides of the inequality.

$\displaystyle \begin{array}{r}4\geq{x}+5 \\\underline{\,\,\,-5\,\,\,\,\,-5}\\-1\,\,\,\,\,\,\,\,\,\,\ge \,\,\,x\end{array}$

Rewrite the inequality with the variable on the left – this makes writing the interval and drawing the graph easier.

$x\le{-1}$

Note how the the pointy part of the inequality is still directed at the variable, so instead of reading as negative one is greater or equal to x, it now reads as x is less than or equal to negative one.

Answer

Inequality: $\left(-\infty,-1\right]$
Graph: Notice that a closed circle is used because the inequality is “less than or equal to” . The blue arrow is drawn to the left of the point $−1$.
$(-oo,-1]$

[/hidden-answer]

Check the solution to $4\geq{x}+5$
[reveal-answer q=”568062″]Show Solution[/reveal-answer]
[hidden-answer a=”568062″]

Substitute the end point $4=x+5$

$\displaystyle \begin{array}{r}4=x+5\,\,\,\\\text{Does}\,\,\,4=-1+5?\\-1=-1\,\,\,\end{array}$

Pick a value less than $−5$, to check in the inequality. (This value will be on the shaded part of the graph.)

$\displaystyle \begin{array}{r}4\geq{-5}+5\,\,\,\\\text{ }\,\text{ Is}\,\,4\ge 0?\\\text{It}\,\text{checks!}\end{array}$

$4\geq{x}+5$[/hidden-answer]

The following video show examples of solving inequalities with the variable on the right side.

$Thumbnail for the embedded element "Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Right Side)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Solve inequalities with multiplication and division

Solving an inequality with a variable that has a coefficient other than 1 usually involves multiplication or division. The steps are like solving one-step equations involving multiplication or division EXCEPT for the inequality sign. Let’s look at what happens to the inequality when you multiply or divide each side by the same number.

Let’s start with the true statement: $10>5$
Next, multiply both sides by the same positive number: $10\cdot-2>5 \\ \,\,\,\,\,\cdot -2\,\cdot-2$
20 is greater than 10, so you still have a true inequality: $−20$ is not greater than $−20>−10$
When you multiply by a positive number, leave the inequality sign as it is!	You must “reverse” the inequality sign to make the statement true: $−20<−10$

$Caution$ Caution! When you multiply or divide by a negative number, “reverse” the inequality sign. Whenever you multiply or divide both sides of an inequality by a negative number, the inequality sign must be reversed in order to keep a true statement. These rules are summarized in the box below.

Multiplication and Division Properties of Inequality

Start With	Multiply By	Final Inequality
$c$	$a>b$	$ac<bc$

Start With	Divide By	Final Inequality
$c$	$a>b$	$\displaystyle \frac{a}{c}<\frac{b}{c}$

Keep in mind that you only change the sign when you are multiplying and dividing by a negative number. If you add or subtract by a negative number, the inequality stays the same.

Example

Solve for x. $3x>12$

[reveal-answer q=”691711″]Show Solution[/reveal-answer]
[hidden-answer a=”691711″]Divide both sides by 3 to isolate the variable.

$\displaystyle \begin{array}{r}\underline{3x}>\underline{12}\\3\,\,\,\,\,\,\,\,\,\,\,\,3\\x>4\,\,\,\end{array}$

Check your solution by first checking the end point 4, and then checking another solution for the inequality.

$\begin{array}{r}3\cdot4=12\\12=12\\3\cdot10>12\\30>12\\\text{It checks!}\end{array}$

Answer

Inequality: $\displaystyle x>4$

Interval: $\left(4,\infty\right)$

Graph: $Number line. Open circle on 4. Highlight through all numbers greater than 4.$

[/hidden-answer]

There was no need to make any changes to the inequality sign because both sides of the inequality were divided by positive 3. In the next example, there is division by a negative number, so there is an additional step in the solution!

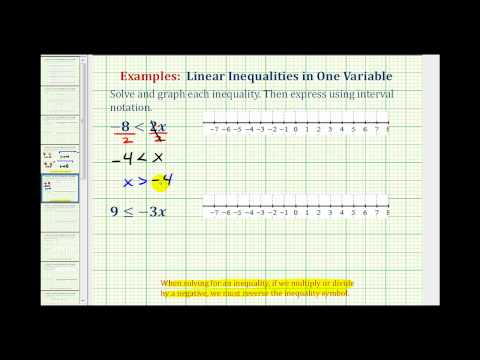
Example

Solve for x. $−2x>6$

[reveal-answer q=”604033″]Show Solution[/reveal-answer]
[hidden-answer a=”604033″]Divide each side of the inequality by $−2$ to isolate the variable, and change the direction of the inequality sign because of the division by a negative number.

$\displaystyle \begin{array}{r}\underline{-2x}<\underline{\,6\,}\\-2\,\,\,\,-2\,\\x<-3\end{array}$

Check your solution by first checking the end point $−3$, and then checking another solution for the inequality.

$\begin{array}{r}-2\left(-3\right)=6 \\6=6\\ -2\left(-6\right)>6 \\ 12>6\end{array}$

It checks!

Answer

Inequality: $\displaystyle x<-3$

Interval: $\left(-\infty, -3\right)$

Graph: $−2$, the inequality symbol was switched from > to <.
[/hidden-answer]

The following video shows examples of solving one step inequalities using the multiplication property of equality where the variable is on the left hand side.

$Thumbnail for the embedded element "Ex: Solve One Step Linear Inequality by Dividing (Variable Left)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Think About It

Before you read the solution to the next example, think about what properties of inequalities you may need to use to solve the inequality. What is different about this example from the previous one? Write your ideas in the box below.

Solve for x. $-\frac{1}{2}>-12x$

[practice-area rows=”1″][/practice-area]
[reveal-answer q=”811465″]Show Solution[/reveal-answer]
[hidden-answer a=”811465″]

This inequality has the variable on the right hand side, which is different from the previous examples. Start the solution process as before, and at the end, you can move the variable to the left to write the final solution.

Divide both sides by $-12$ to isolate the variable. Since you are dividing by a negative number, you need to change the direction of the inequality sign.

$\displaystyle\begin{array}{l}-\frac{1}{2}\gt{-12x}\\\\\frac{-\frac{1}{2}}{-12}\gt\frac{-12x}{-12}\\\end{array}$

Dividing a fraction by an integer requires you to multiply by the reciprocal, and the reciprocal of $\frac{1}{-12}$

$\displaystyle\begin{array}{r}\left(-\frac{1}{12}\right)\left(-\frac{1}{2}\right)\lt\frac{-12x}{-12}\,\,\\\\ \frac{1}{24}\lt\frac{\cancel{-12}x}{\cancel{-12}}\\\\ \frac{1}{24}\lt{x}\,\,\,\,\,\,\,\,\,\,\end{array}$

Answer

Inequality: $x\gt\frac{1}{24}$. Writing the inequality with the variable on the left requires a little thinking, but helps you write the interval and draw the graph correctly.

Interval: $\left(\frac{1}{24},\infty\right)$

Graph: $Open dot on zero with a line through all numbers greater than zero.$

[/hidden-answer]

The following video gives examples of how to solve an inequality with the multiplication property of equality where the variable is on the right hand side.

$Thumbnail for the embedded element "Ex: Solve One Step Linear Inequality by Dividing (Variable Right)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Combine properties of inequality to solve algebraic inequalities

A popular strategy for solving equations, isolating the variable, also applies to solving inequalities. By adding, subtracting, multiplying and/or dividing, you can rewrite the inequality so that the variable is on one side and everything else is on the other. As with one-step inequalities, the solutions to multi-step inequalities can be graphed on a number line.

Example

Solve for p. $4p+5<29$

[reveal-answer q=”211828″]Show Solution[/reveal-answer]
[hidden-answer a=”211828″]

Begin to isolate the variable by subtracting 5 from both sides of the inequality.

$\displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\,\,-5\,\,\,\,\,-5}\\4p\,\,\,\,\,\,\,\,\,<\,\,24\,\,\end{array}$

Divide both sides of the inequality by 4 to express the variable with a coefficient of 1.

$\begin{array}{l}\underline{4p}\,<\,\,\underline{24}\,\,\\\,4\,\,\,\,<\,\,4\\\,\,\,\,\,p<6\end{array}$

Answer

Inequality: $p<6$

Interval: $\left(-\infty,6\right)$

Graph: Note the open circle at the end point 6 to show that solutions to the inequality do not include 6. The values where p is less than 6 are found all along the number line to the left of 6.

$Number line. Open circle on 6. Highlight on every number less than 6.$

[/hidden-answer]

Check the solution.
[reveal-answer q=”291597″]Show Solution[/reveal-answer]
[hidden-answer a=”291597″]

Check the end point 6 in the related equation.

$\displaystyle \begin{array}{r}4p+5=29\,\,\,\\\text{Does}\,\,\,4(6)+5=29?\\24+5=29\,\,\,\\29=29\,\,\,\\\text{Yes!}\,\,\,\,\,\,\end{array}$

Try another value to check the inequality. Let’s use $p=0$.

$\displaystyle \begin{array}{r}4p+5<29\,\,\,\\\text{Is}\,\,\,4(0)+5<29?\\0+5<29\,\,\,\\5<29\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}$

$4p+5<29$

[/hidden-answer]

Example

Solve for x: $3x–7\ge 41$
[reveal-answer q=”238157″]Show Solution[/reveal-answer]
[hidden-answer a=”238157″]

Begin to isolate the variable by adding 7 to both sides of the inequality, then divide both sides of the inequality by 3 to express the variable with a coefficient of 1.

$\displaystyle \begin{array}{l}3x-7\ge 41\\\underline{\,\,\,\,\,\,\,+7\,\,\,\,+7}\\\frac{3x}{3}\,\,\,\,\,\,\,\,\ge \frac{48}{3}\\\,\,\,\,\,\,\,\,\,\,x\ge 16\end{array}$

Answer

Inequality: $x\ge 16$

Interval: $\left[16,\infty\right)$

Graph: To graph this inequality, you draw a closed circle at the end point 16 on the number line to show that solutions include the value 16. The line continues to the right from 16 because all the numbers greater than 16 will also make the inequality $3x–7\ge 41$ true.
$Closed dot on 16, line through all numbers greater than 16.$

[/hidden-answer]

Check the solution.
[reveal-answer q=”437341″]Show Solution[/reveal-answer]

[hidden-answer a=”437341″]

First, check the end point 16 in the related equation.

$\displaystyle \begin{array}{r}3x-7=41\,\,\,\\\text{Does}\,\,\,3(16)-7=41?\\48-7=41\,\,\,\\41=41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}$

Then, try another value to check the inequality. Let’s use $x = 20$.

$\displaystyle \begin{array}{r}\,\,\,\,3x-7\ge 41\,\,\,\\\text{Is}\,\,\,\,\,3(20)-7\ge 41?\\60-7\ge 41\,\,\,\\53\ge 41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}$

[/hidden-answer]

When solving multi-step equations, pay attention to situations in which you multiply or divide by a negative number. In these cases, you must reverse the inequality sign.

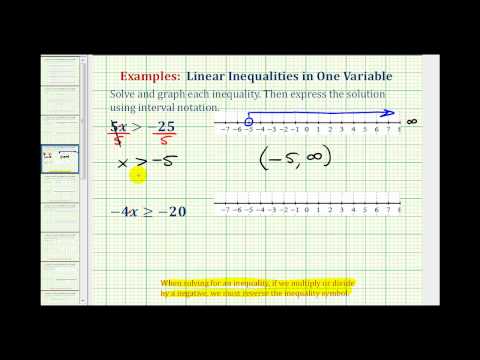
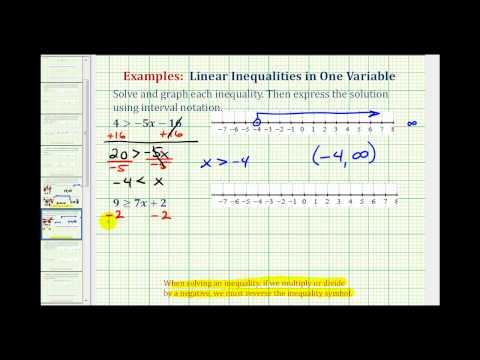
Example

Solve for p. $−58>14−6p$

[reveal-answer q=”424351″]Show Solution[/reveal-answer]
[hidden-answer a=”424351″]

Note how the variable is on the right hand side of the inequality, the method for solving does not change in this case.

Begin to isolate the variable by subtracting 14 from both sides of the inequality.

$\displaystyle \begin{array}{l}−58\,\,>14−6p\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,-14\,\,\,\,\,\,\,-14}\\-72\,\,\,\,\,\,\,\,\,\,\,>-6p\end{array}$

Divide both sides of the inequality by $−6$ to express the variable with a coefficient of 1. Dividing by a negative number results in reversing the inequality sign.

$\begin{array}{l}\underline{-72}>\underline{-6p}\\-6\,\,\,\,\,\,\,\,\,\,-6\\\,\,\,\,\,\,12\lt{p}\end{array}$

We can also write this as $p>12$. Notice how the inequality sign is still opening up toward the variable p.

Answer

Inequality: $\left(12,\infty\right)$
Graph: The graph of the inequality p > 12 has an open circle at 12 with an arrow stretching to the right.

$Number line. Open circle on 12. Highlight on all numbers over 12.$

[/hidden-answer]

Check the solution.
[reveal-answer q=”500309″]Show Solution[/reveal-answer]
[hidden-answer a=”500309″]

First, check the end point 12 in the related equation.

$\begin{array}{r}-58=14-6p\\-58=14-6\left(12\right)\\-58=14-72\\-58=-58\end{array}$

Then, try another value to check the inequality. Try 100.

$\begin{array}{r}-58>14-6p\\-58>14-6\left(100\right)\\-58>14-600\\-58>-586\end{array}$

[/hidden-answer]

In the following video, you will see an example of solving a linear inequality with the variable on the left side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

$Thumbnail for the embedded element "Ex: Solve a Two Step Linear Inequality (Variable Left)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

In the following video, you will see an example of solving a linear inequality with the variable on the right side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

$Thumbnail for the embedded element "Ex: Solve a Two Step Linear Inequality (Variable Right)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Simplify and solve algebraic inequalities using the distributive property

As with equations, the distributive property can be applied to simplify expressions that are part of an inequality. Once the parentheses have been cleared, solving the inequality will be straightforward.

Example

Solve for x. $2\left(3x–5\right)\leq 4x+6$

[reveal-answer q=”587737″]Show Solution[/reveal-answer]
[hidden-answer a=”587737″]

Distribute to clear the parentheses.

$\displaystyle \begin{array}{r}\,2(3x-5)\leq 4x+6\\\,\,\,\,6x-10\leq 4x+6\end{array}$

Subtract 4x from both sides to get the variable term on one side only.

$\begin{array}{r}6x-10\le 4x+6\\\underline{-4x\,\,\,\,\,\,\,\,\,\,\,\,\,\,-4x}\,\,\,\,\,\,\,\,\,\\\,\,\,2x-10\,\,\leq \,\,\,\,\,\,\,\,\,\,\,\,6\end{array}$

Add 10 to both sides to isolate the variable.

$\begin{array}{r}\\\,\,\,2x-10\,\,\le \,\,\,\,\,\,\,\,6\,\,\,\\\underline{\,\,\,\,\,\,+10\,\,\,\,\,\,\,\,\,+10}\\\,\,\,2x\,\,\,\,\,\,\,\,\,\,\,\le \,\,\,\,\,16\,\,\,\end{array}$

Divide both sides by 2 to express the variable with a coefficient of 1.

$\begin{array}{r}\underline{2x}\le \,\,\,\underline{16}\\\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\le \,\,\,\,\,8\end{array}$

Answer

Inequality: $\left(-\infty,8\right]$
Graph: The graph of this solution set includes 8 and everything left of 8 on the number line.

$Number line with the interval (-oo,8] graphed$

[/hidden-answer]

Check the solution.
[reveal-answer q=”808701″]Show Solution[/reveal-answer]
[hidden-answer a=”808701″]

First, check the end point 8 in the related equation.

$\displaystyle \begin{array}{r}2(3x-5)=4x+6\,\,\,\,\,\,\\2(3\,\cdot \,8-5)=4\,\cdot \,8+6\\\,\,\,\,\,\,\,\,\,\,\,2(24-5)=32+6\,\,\,\,\,\,\\2(19)=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\38=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}$

Then, choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 0.

$\displaystyle \begin{array}{l}2(3\,\cdot \,0-5)\le 4\,\cdot \,0+6?\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2(-5)\le 6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-10\le 6\,\,\end{array}$

$\left(-\infty,8\right]$

[/hidden-answer]

In the following video, you are given an example of how to solve a multi-step inequality that requires using the distributive property.

$Thumbnail for the embedded element "Ex: Solve a Linear Inequality Requiring Multiple Steps (One Var)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Think About It

In the next example, you are given an inequality with a term that looks complicated. If you pause and think about how to use the order of operations to solve the inequality, it will hopefully seem like a straightforward problem. Use the textbox to write down what you think is the best first step to take.

Solve for a. \(\displaystyle\frac

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/1.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[3]/div/p[2]/span[1], line 1, column 2

6{<2}\)

[practice-area rows=”1″][/practice-area]

[reveal-answer q=”701072″]Show Solution[/reveal-answer]

[hidden-answer a=”701072″]

Clear the fraction by multiplying both sides of the equation by 6.

\(\displaystyle \begin{array}{r}\frac

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/1.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[3]/div/p[7]/span[1], line 1, column 2

6{<2}\,\,\,\,\,\,\,\,\\\\6\,\cdot \,\frac{2a-4}{6}<2\,\cdot \,6\\\\{2a-4}<12\,\,\,\,\,\,\end{array}\)

Add 4 to both sides to isolate the variable.

$\displaystyle \begin{array}{r}2a-4<12\\\underline{\,\,\,+4\,\,\,\,+4}\\2a<16\end{array}$

Divide both sides by 2 to express the variable with a coefficient of 1.

$\displaystyle \begin{array}{c}\frac{2a}{2}<\,\frac{16}{2}\\\\a<8\end{array}$

Answer

Inequality: $a<8$

Interval: $\left(-\infty,8\right)$

Graph: The graph of this solution contains a solid dot at 8 to show that 8 is included in the solution set. The line continues to the left to show that values less than 8 are also included in the solution set. $Open circle on 8 and line through all numbers less than 8.$

[/hidden-answer]

Check the solution.
[reveal-answer q=”905072″]Show Solution[/reveal-answer]

[hidden-answer a=”905072″]
First, check the end point 8 in the related equation.

$\displaystyle \begin{array}{r}\frac{2a-4}{6}=2\,\,\,\,\\\\\text{Does}\,\,\,\frac{2(8)-4}{6}=2?\\\\\frac{16-4}{6}=2\,\,\,\,\\\\\frac{12}{6}=2\,\,\,\,\\\\2=2\,\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}$

Then choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 5.

$\displaystyle \begin{array}{r}\text{Is}\,\,\,\frac{2(5)-4}{6}<2?\\\\\frac{10-4}{6}<2\,\,\,\\\\\,\,\,\,\frac{6}{6}<2\,\,\,\\\\1<2\,\,\,\\\\\text{Yes!}\,\,\,\,\,\end{array}$

[/hidden-answer]

Summary

Solving inequalities is very similar to solving equations, except you have to reverse the inequality symbols when you multiply or divide both sides of an inequality by a negative number. There are three ways to represent solutions to inequalities: an interval, a graph, and an inequality. Because there is usually more than one solution to an inequality, when you check your answer you should check the end point and one other value to check the direction of the inequality.

Inequalities can have a range of answers. The solutions are often graphed on a number line in order to visualize all of the solutions. Multi-step inequalities are solved using the same processes that work for solving equations with one exception. When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol. The inequality symbols stay the same whenever you add or subtract either positive or negative numbers to both sides of the inequality.

Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
Graph Linear Inequalities in One Variable (Basic). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/-kiAeGbSe5c. License: CC BY: Attribution
Given Interval in Words, Graph and Give Inequality. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/E_ZWNVNEvOg. License: CC BY: Attribution
Given an Inequality, Graph and Give Interval Notation. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/BKhDzNKjVBc. License: CC BY: Attribution
Given Interval in Words, Graph and Give Interval Notation. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/OYkQ-McI2qg. License: CC BY: Attribution
Given Interval Notation, Graph and Give Inequality. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/lkhILNEPbfk. License: CC BY: Attribution
Screenshot: Cecilia Venn Diagram. Authored by: Lumen Learning. License: CC BY: Attribution
Screenshot: Internet Privacy. Authored by: Lumen Learning. License: CC BY: Attribution
Solutions to Basic OR Compound Inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/nKarzhZOFIk. License: CC BY: Attribution
Solutions to Basic AND Compound Inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/LP3fsZNjJkc. License: CC BY: Attribution

Unit 10: Solving Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Left Side). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/1Z22Xh66VFM. License: CC BY: Attribution
Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Right Side). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/RBonYKvTCLU. License: CC BY: Attribution
Ex: Solve One Step Linear Inequality by Dividing (Variable Left). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/IajiD3R7U-0. License: CC BY: Attribution
Ex: Solve One Step Linear Inequality by Dividing (Variable Right). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/s9fJOnVTHhs. License: CC BY: Attribution
Ex: Graph Basic Inequalities and Express Using Interval Notation. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/X0xrHKgbDT0. License: CC BY: Attribution
College Algebra. Authored by: Jay Abramson, et al.. Located at: courses.candelalearning.com/collegealgebra1xmaster/. License: CC BY: Attribution
Ex: Graph Basic Inequalities and Express Using Interval Notation. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/X0xrHKgbDT0. License: CC BY: Attribution
Ex: Solve a Two Step Linear Inequality (Variable Left). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/RB9wvIogoEM. License: CC BY: Attribution
Ex: Solve a Two Step Linear Inequality (Variable Right). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/9D2g_FaNBkY. License: CC BY: Attribution
Ex: Solve a Linear Inequality Requiring Multiple Steps (One Var). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/vjZ3rQFVkh8. License: Public Domain: No Known Copyright
Ex: Solve a Compound Inequality Involving OR (Union). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/oRlJ8G7trR8. License: CC BY: Attribution
Ex 1: Solve and Graph Basic Absolute Value inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/0cXxATY2S-k. License: CC BY: Attribution
Ex 2: Solve and Graph Absolute Value inequalities Mathispower4u . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/d-hUviSkmqE. License: CC BY: Attribution
Ex 3: Solve and Graph Absolute Value inequalitie. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/ttUaRf-GzpM. License: CC BY: Attribution
Ex 4: Solve and Graph Absolute Value inequalities (Requires Isolating Abs. Value). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/5jRUuiMUxWQ. License: CC BY: Attribution
College Algebra. Authored by: Jay Abramson, et. al. Located at: courses.candelalearning.com/collegealgebra1xmaster/. License: CC BY: Attribution

Symbol	Words	Example
\({2}\neq{8}\), 2 is not equal to 8.
\({5}\gt{1}\), 5 is greater than 1
\({2}\lt{11}\), 2 is less than 11
\({4}\geq{ 4}\), 4 is greater than or equal to 4
\({7}\leq{9}\), 7 is less than or equal to 9

Inequality	Words	Interval Notation
\(\left(a,b\right)\)
\(\left(a,\infty \right)\)
\(\left(-\infty ,b\right)\)
\(\left[a,\infty \right)\)
\(\left(-\infty ,b\right]\)
\(\left[a,b\right)\)
\(\left(a,b\right]\)
\(\left[a,b\right]\)
\(\left(-\infty ,a\right)\cup \left(b,\infty \right)\)
All real numbers	All real numbers	\(\left(-\infty ,\infty \right)\)

Let’s start with the true statement: \(10>5\)
Next, multiply both sides by the same positive number: \(10\cdot-2>5 \\ \,\,\,\,\,\cdot -2\,\cdot-2\)
20 is greater than 10, so you still have a true inequality: \(−20\) is not greater than \(−20>−10\)
When you multiply by a positive number, leave the inequality sign as it is!	You must “reverse” the inequality sign to make the statement true: \(−20<−10\)

Search

Text Color

Text Size

Margin Size

Font Type

Think About It

Addition and Subtraction Properties of Inequality

Example

Answer

Example

Example

Answer

Answer

Answer

Solve inequalities with multiplication and division

Multiplication and Division Properties of Inequality

Example

Answer

Example

Answer

Think About It

Answer

Answer

Answer

Answer

Answer

Think About It

Answer