2.5: Writing Equations of Lines
- Page ID
- 51450
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Write the equation and draw the graph of a line using slope and y-intercept
- Write the equation of a line using slope and y-intercept
- Rearrange a linear equation so it is in slope-intercept form.
- Graph a line using slope and y-intercept
- Write and solve equations of lines using slope and a point on the line
- Write the equation of a line given the slope and a point on the line.
- Identify which parts of a linear equation are given and which parts need to be solved for using algebra
- Write and solve equations of lines using two points on the line
- Write the equation of a line given two points on the line
- Identify which parts of a linear equation are given and which parts need to be solved for using algebra.
- Write equations of parallel and perpendicular lines
- Find a line that is parallel to another line given a point
- Find a line that is perpendicular to another line given a point
- Interpret the y-intercept of a linear equation and use that equation to make predictions
- Interpret the y-intercept of a linear equation
- Use a linear equation to make a prediction
When graphing a line we found one method we could use is to make a table of values. However, if we can identify some properties of the line, we may be able to make a graph much quicker and easier. One such method is finding the slope and the y-intercept of the equation. The slope can be represented by m and the y-intercept, where it crosses the axis and \((0,b)\) where b is the value where the graph crosses the vertical y-axis. Any other point on the line can be represented by \((x,y)\).
In the equation,
\(y = mx + b\)
\(\begin{array}{l}\,\,\,\,\,m\,\,\,\,=\,\,\,\text{slope}\\(x,y)=\,\,\,\text{a point on the line}\\\,\,\,\,\,\,\,b\,\,\,\,=\,\,\,\text{the y value of the y-intercept}\end{array}\)
This formula is known as the slope-intercept equation. If we know the slope and the y-intercept we can easily find the equation that represents the line
Example
Write the equation of the line that has a slope of \(−5\).
[reveal-answer q=”624715″]Show Solution[/reveal-answer]
[hidden-answer a=”624715″]Substitute the slope (m) into \(y=mx+b\).
\(\displaystyle y=\frac{1}{2}x+b\)
Substitute the y-intercept (b) into the equation.
\(\displaystyle y=\frac{1}{2}x-5\)
Answer
\(y=\frac{1}{2}x-5\)
[/hidden-answer]
We can also find the equation by looking at a graph and finding the slope and y-intercept.
Example
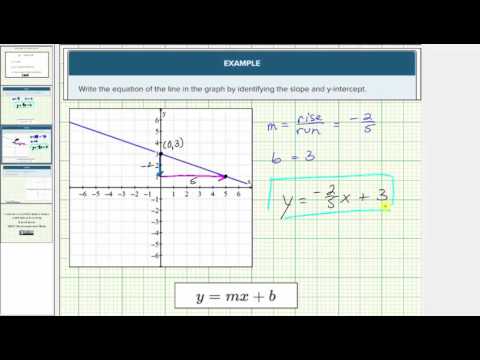
Write the equation of the line in the graph by identifying the slope and y-intercept.
\((0,3)\). This means the y-intercept is 3.
Identify one other point and draw a slope triangle to find the slope.
The slope is \(\frac{-2}{3}\)
Substitute the slope and y value of the intercept into the slope-intercept equation.
\(y=mx+b\\y=\frac{-2}{3}x+b\\y=\frac{-2}{3}x+3\)
Answer
\(y=\frac{-2}{3}x+3\)
[/hidden-answer]
We can also move the opposite direction, using the equation identify the slope and y-intercept and graph the equation from this information. However, it will be important for the equation to first be in slope intercept form. If it is not, we will have to solve it for y so we can identify the slope and the y-intercept.
Example
Write the following equation in slope-intercept form.
\(2x+4y=6\)
[reveal-answer q=”373034″]Show Solution[/reveal-answer]
[hidden-answer a=”373034″]We need to solve for y. Start by subtracting \(2\) from both sides.
\(\begin{array}{r}2x\,\,\,+\,\,\,4y\,\,\,=\,\,\,6\\-2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-2x\end{array}\)
It helps to place the x term first on the right hand side. Notice how we keep the 6 positive by placing an addition sign in front.
\(4y=-2x+6\)
Divide each term by 4 to isolate the y.
\(\frac{4y}{4}=\frac{-2x}{4}+\frac{6}{4}\)
\(y=\frac{-2x}{4}+\frac{6}{4}\)
Reduce the fractions
\(y=-\frac{1}{2}x+\frac{3}{2}\)
Answer
\(y=-\frac{1}{2}x+\frac{3}{2}\)
[/hidden-answer]
Once we have an equation in slope-intercept form we can graph it by first plotting the y-intercept, then using the slope, find a second point and connecting the dots.
Example
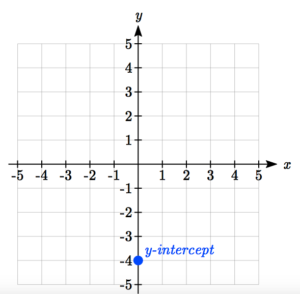
Graph \(y=\frac{1}{2}x-4\) using the slope-intercept equation.
[reveal-answer q=”420487″]Show Solution[/reveal-answer]
[hidden-answer a=”420487″]First, plot the y-intercept.
Now use the slope to count up or down and over left or right to the next point. This slope is \(\frac{1}{2}\), so you can count up one and right two—both positive because both parts of the slope are positive.
Connect the dots.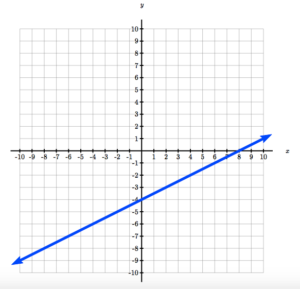
[/hidden-answer]
Slope-Intercept Form of a Line
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Find the Equation of a Line Given the Slope and a Point on the Line
Using the slope-intercept equation of a line is possible when you know both the slope (m) and the y-intercept (b), but what if you know the slope and just any point on the line, not specifically the y-intercept? Can you still write the equation? The answer is yes, but you will need to put in a little more thought and work than you did previously.
Recall that a point is an (x, y) coordinate pair and that all points on the line will satisfy the linear equation. So, if you have a point on the line, it must be a solution to the equation. Although you don’t know the exact equation yet, you know that you can express the line in slope-intercept form, \(y=mx+b\).
You do know the slope (m), but you just don’t know the value of the y-intercept (b). Since point (x, y) is a solution to the equation, you can substitute its coordinates for x and y in \(y=mx+b\) and solve to find b!
This may seem a bit confusing with all the variables, but an example with an actual slope and a point will help to clarify.
Example
Write the equation of the line that has a slope of 3 and contains the point \((1,4)\).
[reveal-answer q=”161353″]Show Solution[/reveal-answer]
[hidden-answer a=”161353″]
Substitute the slope (m) into \(y=mx+b\).
\(y=3x+b\)
Substitute the point \((1,4)\) for x and y.
\(4=3\left(1\right)+b\)
Solve for b.
\(\begin{array}{l}4=3+b\\1=b\end{array}\)
Rewrite \(m=3\) and \(b=1\).
Answer
\(y=3x+1\)[/hidden-answer]
To confirm our algebra, you can check by graphing the equation \((1,4)\).
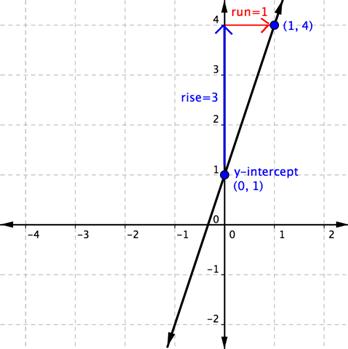
If you know the slope of a line and a point on the line, you can draw a graph. Using an equation in the point-slope form allows you to identify the slope and a point. Consider the equation \(\displaystyle y=-3x-1\). The y-intercept is the point on the line where it passes through the y-axis. What is the value of x at this point?
Therefore, you can tell from this equation that the y-intercept is at \((0,−1)\), on a graph.
You can also tell from the equation that the slope of this line is \((0,−1)\) and count up 3 and over \(\displaystyle y=-3x-1\).
Example (Advanced)
Write the equation of the line that has a slope of \(\left(4,\frac{5}{4}\right)\).
[reveal-answer q=”31452″]Show Solution[/reveal-answer]
[hidden-answer a=”31452″]
Substitute the slope (m) into \(y=mx+b\).
\(\begin{array}{l}y=mx+b\\\\y=-\frac{7}{8}x+b\end{array}\)
Substitute the point \(\left(4,\frac{5}{4}\right)\) for x and y.
\(\frac{5}{4}=-\frac{7}{8}\left(4\right)+b\)
Solve for b.
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\frac{5}{4}=-\frac{28}{8}+b\\\\\,\,\,\,\,\,\,\,\,\,\,\,\frac{5}{4}=-\frac{14}{4}+b\\\\\frac{5}{4}+\frac{14}{4}=-\frac{14}{4}+\frac{14}{4}+b\\\\\,\,\,\,\,\,\,\,\,\,\frac{19}{4}=b\end{array}\)
Rewrite \(\displaystyle m=-\frac{7}{8}\) and \(\displaystyle b=\frac{19}{4}\).
Answer
\(y=-\frac{7}{8}x+\frac{19}{4}\)[/hidden-answer]
Video: Find the Equation of a Line Given the Slope and a Point on the Line
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Find the Equation of a Line Given Two Points on the Line
Let’s suppose you don’t know either the slope or the y-intercept, but you do know the location of two points on the line. It is more challenging, but you can find the equation of the line that would pass through those two points. You will again use slope-intercept form to help you.
The slope of a linear equation is always the same, no matter which two points you use to find the slope. Since you have two points, you can use those points to find the slope (m). Now you have the slope and a point on the line! You can now substitute values for m, x, and y into the equation \(y=mx+b\) and find b.
Example
Write the equation of the line that passes through the points \((−1,−5)\).
[reveal-answer q=”333536″]Show Solution[/reveal-answer]
[hidden-answer a=”333536″]
Find the slope using the given points.
\(\displaystyle \frac{1-(-5)}{2-(-1)}=\frac{6}{3}=2\)
Substitute the slope (m) into \(y=mx+b\).
\(y=2x+b\)
Substitute the coordinates of either point for x and y– this example uses (2, 1).
\(1=2(2)+b\)
Solve for b.
\(\begin{array}{l}\,\,\,\,1=4+b\\−3=b\end{array}\)
Rewrite \(m=2\) and \(b=-3\).
Answer
\(\begin{array}{l}y=2x+\left(-3\right)\\\,\,\,\,\,\,\,\,\,\,\,\text{or}\\y=2x-3\end{array}\)[/hidden-answer]
Notice that is doesn’t matter which point you use when you substitute and solve for b—you get the same result for b either way. In the example above, you substituted the coordinates of the point (2, 1) in the equation \(y=2x+b\), but substitute in \((−1,−5)\):
\(\begin{array}{l}\,\,\,\,\,y=2x+b\\-5=2\left(-1\right)+b\\-5=-2+b\\-3=b\end{array}\)
The final equation is the same: \(y=2x–3\).
Example (Advanced)
Write the equation of the line that passes through the points \((1.15,7.6)\).
[reveal-answer q=”347882″]Show Solution[/reveal-answer]
[hidden-answer a=”347882″]
Find the slope using the given points.
\(\displaystyle \frac{7.6-6.45}{1.15-(-4.6)}=\frac{1.15}{5.75}=0.2\)
Substitute the slope (m) into \(\displaystyle y=mx+b\).
\(\displaystyle y=0.2x+b\)
Substitute either point for x and y—this example uses \((1.15,7.6)\). Then solve for b.
\(\displaystyle \begin{array}{l}\,\,\,\,\,\,7.6\,\,=\,\,0.2(1.15)+b\\\,\,\,\,\,\,7.6\,\,=\,\,0.23+b\\\,\,\,\,\,\,7.6\,\,=\,\,0.23+b\\\underline{-0.23\,\,\,\,-0.23}\\\,\,\,\,\,7.37\,=\,\,b\end{array}\)
Rewrite \(m=0.2\) and \(b=7.37\).
\(\displaystyle y=0.2x+7.37\)
Answer
The equation of the line that passes through the points \((1.15,7.6)\) is \(y=0.2x+7.37\).[/hidden-answer]
Video: Find the Equation of a Line Given Two Points on the Line
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Write the equations of parallel and perpendicular lines
The relationships between slopes of parallel and perpendicular lines can be used to write equations of parallel and perpendicular lines.
Let’s start with an example involving parallel lines.
Example
Write the equation of a line that is parallel to the line \((−2,1)\).
[reveal-answer q=”763534″]Show Solution[/reveal-answer]
[hidden-answer a=”763534″]
Rewrite the line you want to be parallel to into the \(y=mx+b\) form, if needed.
\(\begin{array}{r}x–y=5\,\,\,\,\,\,\,\,\,\,\,\,\,\\−y=−x+5\\y=x–5\,\,\,\,\,\,\,\end{array}\)
Identify the slope of the given line.
In the equation above, \(b=−5\).
Since \(m=1\), the slope is 1.
To find the slope of a parallel line, use the same slope.
The slope of the parallel line is 1.
Use the method for writing an equation from the slope and a point on the line. Substitute 1 for m, and the point \((−2,1)\) for x and y.
\(\begin{array}{l}y=mx+b\\1=1(−2)+b\end{array}\)
Solve for b.
\(\begin{array}{l}1=−2+b\\3=b\end{array}\)
Write the equation using the new slope for m and the b you just found.
Answer
\(y=x+3\)[/hidden-answer]
Determine the Equation of a Line Parallel to Another Line Through a Given Point
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Determine the Equation of a Line Perpendicular to Another Line Through a Given Point
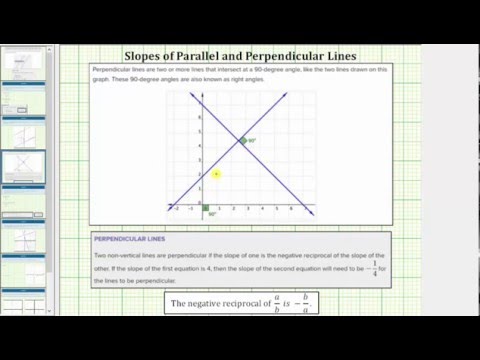
When you are working with perpendicular lines, you will usually be given one of the lines and an additional point. Remember that two non-vertical lines are perpendicular if the slope of one is the negative reciprocal of the slope of the other. To find the slope of a perpendicular line, find the reciprocal, and then find the opposite of this reciprocal. In other words, flip it and change the sign.
Example
Write the equation of a line that contains the point \(y=2x– 6\).
[reveal-answer q=”604282″]Show Solution[/reveal-answer]
[hidden-answer a=”604282″]
Identify the slope of the line you want to be perpendicular to.
The given line is written in \(m=2\) and \(b=-6\). The slope is 2.
To find the slope of a perpendicular line, find the reciprocal, \(\displaystyle -\frac{1}{2}\).
The slope of the perpendicular line is \(\displaystyle -\frac{1}{2}\).
Use the method for writing an equation from the slope and a point on the line. Substitute \((1,5)\) for x and y.
\(\displaystyle \begin{array}{l}y=mx+b\\5=-\frac{1}{2}(1)+b\end{array}\)
Solve for b.
\(\displaystyle \begin{array}{l}\,\,\,5=-\frac{1}{2}+b\\\frac{11}{2}=b\end{array}\)
Write the equation using the new slope for m and the b you just found.
Answer
\(y=-\frac{1}{2}x+\frac{11}{2}\)[/hidden-answer]
Determine the Equation of a Line Perpendicular to a Line in Slope-Intercept Form
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Example
Write the equation of a line that is parallel to the line \((0,10)\).
[reveal-answer q=”426450″]Show Solution[/reveal-answer]
[hidden-answer a=”426450″]
Rewrite the line into \(y=mx+b\) form, if needed.
You may notice without doing this that \(y=4\) is a horizontal line 4 units above the x-axis. Because it is horizontal, you know its slope is zero.
\(\begin{array}{l}y=4\\y=0x+4\end{array}\)
Identify the slope of the given line.
In the equation above, \(b=4\).
Since \(m=0\), the slope is 0. This is a horizontal line.
To find the slope of a parallel line, use the same slope.
The slope of the parallel line is also 0.
Since the parallel line will be a horizontal line, its form is
\(y=\text{a constant}\)
Since we want this new line to pass through the point \((0,10)\), we will need to write the equation of the new line as:
\(y=10\)
This line is parallel to \((0,10)\).
Answer
\(y=10\)[/hidden-answer]
Example
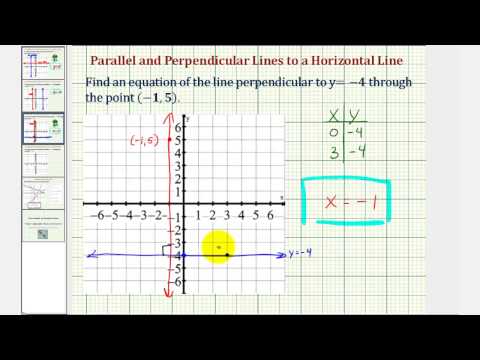
Write the equation of a line that is perpendicular to the line \((-2,5)\).
[reveal-answer q=”426550″]Show Solution[/reveal-answer]
[hidden-answer a=”426550″]
In the equation above, \(b=-3\).
A perpendicular line will have a slope that is the negative reciprocal of the slope of \(y=-3\), but what does that mean in this case?
The reciprocal of 0 is \(\frac{1}{0}\), but we know that dividing by 0 is undefined.
This means that we are looking for a line whose slope is undefined, and we also know that vertical lines have slopes that are undefined. This makes sense since we started with a horizontal line.
The form of a vertical line is \((-2,5)\), all of the x-values on this line must be \(-2\).
The equation of a line passing through \(y=-3\) is therefore,
\(x=-2\)
Answer
\(x=-2\)[/hidden-answer]
Find the Equation of a Perpendicular and Horizontal Line to a Horizontal Line
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Interpret the y-intercept of a linear equation
Often, when the line in question represents a set of data or observations, the y-intercept can be interpreted as a starting point. We will continue to use the examples for house value in Mississippi and Hawaii and high school smokers to interpret the meaning of the y-intercept in those equations.
Example
Recall the equations and data for house value:
Linear equations describing the change in median home values between 1950 and 2000 in Mississippi and Hawaii are as follows:
Hawaii: \(y = 3966x+74,400\)
Mississippi: \(y = 924x+25,200\)
The equations are based on the following dataset.
x = the number of years since 1950, and y = the median value of a house in the given state.
| Year (x) | Mississippi House Value (y) | Hawaii House Value (y) |
|---|---|---|
| 0 | $25,200 | $74,400 |
| 50 | $71,400 | $272,700 |
And the equations and data for high school smokers:
A linear equation describing the change in the number of high school students who smoke, in a group of 100, between 2011 and 2015 is given as:
\(y = -1.75x+16\)
And is based on the data from this table, provided by the Centers for Disease Control.
x = the number of years since 2011, and y = the number of high school smokers per 100 students.
| Year | Number of High School Students Smoking Cigarettes (per 100) |
| 0 | 16 |
| 4 | 9 |
Also recall that the equation of a line in slope-intercept form is as follows:
\(y = mx + b\)
\(\begin{array}{l}\,\,\,\,\,m\,\,\,\,=\,\,\,\text{slope}\\(x,y)=\,\,\,\text{a point on the line}\\\,\,\,\,\,\,\,b\,\,\,\,=\,\,\,\text{the y value of the y-intercept}\end{array}\)
The examples that follow show how to interpret the y-intercept of the equations used to model house value and the number of high school smokers. Additionally, you will see how to use the equations to make predictions about house value and the number of smokers in future years.
Example
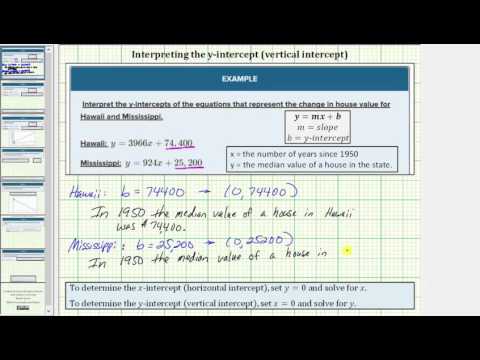
Interpret the y-intercepts of the equations that represent the change in house value for Hawaii and Mississippi.
Hawaii: \(y = 3966x+74,400\)
Mississippi: \(y = 924x+25,200\)
The y-intercept of a two-variable linear equation can be found by substituting 0 in for x.
Hawaii
\(y = 3966x+74,400\\y = 3966(0)+74,400\\y = 74,400\)
The y-intercept is a point, so we write it as (0, 74,400). Remember that y-values represent dollars and x values represent years. When the year is 0—in this case 0 because that is the first date we have in the dataset—the price of a house in Hawaii was $74,400.
Mississippi
\(y = 924x+25,200\\y = 924(0)+25,200\\y = 25,200\)
The y-intercept is (0, 25,200). This means that in 1950 the value of a house in Mississippi was $25,200. Remember that x represents the number of years since 1950, so if \(x=0\) the year is 1950.
Example
Interpret the y-intercept of the equation that represents the change in the number of high school students who smoke out of 100.
Substitute 0 in for x.
\(y = -1.75x+16\\y = -1.75(0)+16\\y = 16\)
The y-intercept is \((0,16)\). The data starts at 2011, so we represent that year as 0. We can interpret the y-intercept as follows:
In the year 2011, 16 out of every 100 high school students smoked.
In the following video you will see an example of how to interpret the y- intercept given a linear equation that represents a set of data.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Use a linear equation to make a prediction
Another useful outcome we gain from writing equations from data is the ability to make predictions about what may happen in the future. We will continue our analysis of the house price and high school smokers. In the following examples you will be shown how to predict future outcomes based on the linear equations that model current behavior.
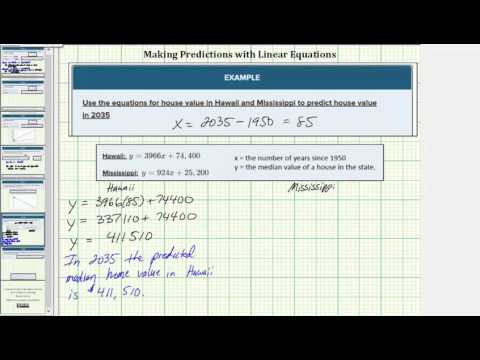
Example
Use the equations for house value in Hawaii and Mississippi to predict house value in 2035.
We are asked to find house value, y, when the year, x, is 2035. Since the equations we have represent house value increase since 1950, we have to be careful. We can’t just plug in 2035 for x, because x represents the years since 1950.
How many years are between 1950 and 2035? \(2035 - 1950 = 85\)
This is our x-value.
For Hawaii:
\(y = 3966x+74,400\\y = 3966(85)+74,400\\y = 337110+74,400 = 411,510\)
Holy cow! The average price for a house in Hawaii in 2035 is predicted to be $411,510 according to this model. See if you can find the current average value of a house in Hawaii. Does the model measure up?
For Mississippi:
\(y = 924x+25,200\\y = 924(85)+25,200\\y = 78540+25,200 = 103,740\)
The average price for a home in Mississippi in 2035 is predicted to be $103,740 according to the model. See if you can find the current average value of a house in Mississippi. Does the model measure up?
In the following video, you will see the example of how to make a prediction with the home value data.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Example
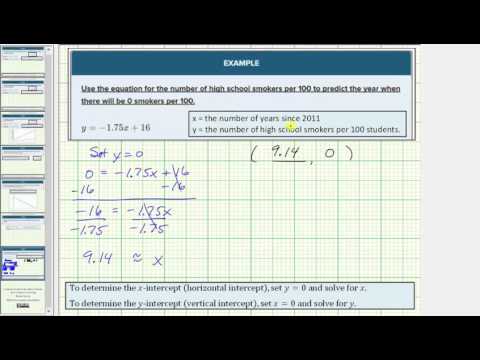
Use the equation for the number of high school smokers per 100 to predict the year when there will be 0 smokers per 100.
\(y = -1.75x+16\)
This question takes a little more thinking. In terms of x and y, what does it mean to have 0 smokers? Since y represents the number of smokers and x represent the year, we are being asked when y will be 0.
Substitute 0 for y.
\(y = -1.75x+16\)
\(0 = -1.75x+16\)
\(-16 = -1.75x\)
\(\frac{-16}{-1.75} = x\)
\(x = 9.14\) years
Again, like the last example, x is representing the number of years since the start of the data—which was 2011, based on the table:
| Year | Number of High School Students Smoking Cigarettes (per 100) |
| 0 | 16 |
| 4 | 9 |
So we are predicting that there will be no smokers in high school by \(2011+9.14=2020\). How accurate do you think this model is? Do you think there will ever be 0 smokers in high school?
The following video gives a thorough explanation of making a prediction given a linear equation.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=68
Bringing it Together
The last example we will show will include many of the concepts that we have been building up throughout this section. We will interpret a word problem, write a linear equation from it, graph the equation, interpret the y-intercept and make a prediction. Hopefully this example will help you to make connections between the concepts we have presented.
Example
It costs $600 to purchase an iphone, plus $55 per month for unlimited use and data.
Write a linear equation that represents the cost, y, of owning and using the iPhone for x amount of months. When you have written your equation, answer the following questions:
- What is the total cost you’ve paid after owning and using your phone for 24 months?
- If you have spent $2,580 since you purchased your phone, how many months have you used your phone?
[reveal-answer q=”282349″]Show Solution[/reveal-answer]
[hidden-answer a=”282349″][/hidden-answer]
Read and Understand: We need to write a linear equation that represents the cost of owning and using an iPhone for any number of months. We are to use y to represent cost, and x to represent the number of months we have used the phone.
Define and Translate: We will use the slope-intercept form of a line, \(y=mx+b\), because we are given a starting cost and a monthly cost for use. We will need to find the slope and the y-intercept.
Slope: in this case we don’t know two points, but we are given a rate in dollars for monthly use of the phone. Our units are dollars per month because slope is \(\frac{55\text{ dollars }}{1\text{ month }}\). \(m=\frac{55}{1}=55\)
Y-Intercept: the y-intercept is defined as a point \(b=600\)
Write and Solve: Substitute the slope and intercept you defined into the slope=intercept equation.
\(\begin{array}{c}y=mx+b\\y=55x+600\end{array}\)
Now we will answer the following questions:
- What is the total cost you’ve paid after owning and using your phone for 24 months?
Since x represents the number of months you have used the phone, we can substitute x=24 into our equation.
\(\begin{array}{c}y=55x+600\\y=55\left(24\right)+600\\y=1320+600\\y=1920\end{array}\)
Y represents the cost after x number of months, so in this scenario, after 24 months, you have spent $1920 to own and use an iPhone.
- If you have spent $2,580 since you purchased your phone, how many months have you used your phone?
We know that y represents cost, and we are given a cost and asked to find the number of months related to having spent that much. We will substitute y=$2,580 into the equation, then use what we know about solving linear equations to isolate x:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y=55x+600\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2580=55x+600\\\text{ subtract 600 from each side}\,\,\,\,\,\,\,\underline{-600}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-600}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1980=55x\\\text{}\\\text{ divide each side by 55 }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1980}{55}=\frac{55x}{55}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,36=x\end{array}\)
If you have spent $2,580 then you have been using your iPhone for 36 months, or 3 years.
Summary
The slope-intercept form of a linear equation is written as \((0,b)\). When you know the slope and the y-intercept of a line you can use the slope-intercept form to immediately write the equation of that line. The slope-intercept form can also help you to write the equation of a line when you know the slope and a point on the line or when you know two points on the line.
When lines in a plane are parallel (that is, they never cross), they have the same slope. When lines are perpendicular (that is, they cross at a 90° angle), their slopes are opposite reciprocals of each other. The product of their slopes will be \(-1\), except in the case where one of the lines is vertical causing its slope to be undefined. You can use these relationships to find an equation of a line that goes through a particular point and is parallel or perpendicular to another line.
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Slope-Intercept Form of a Line. Authored by: Mathispower4u. License: Public Domain: No Known Copyright
- Ex: Determine a Linear Equation Given Slope and a Point (Slope-Intercept Form) . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/URYnKqEctgc. License: CC BY: Attribution
- Ex 1: Find the Equation of a Line in Slope Intercept Form Given Two Points. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/P1ex_a6iYDo. License: CC BY: Attribution
- Unit 13: Graphing, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Determine the Equation of a Line Parallel to a Line in General Form. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/TQKz2XHI09E. License: CC BY: Attribution
- Determine the Equation of a Line Perpendicular to a Line in Slope-Intercept Form. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/QtvtzKjtowA. License: CC BY: Attribution
- Find the Equation of a Perpendicular and Horizontal Line to a Horizontal Line. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/Qpn3f3wMeIs. License: CC BY: Attribution
- Beginning and Intermediate Algebra. Authored by: Tyler Wallace. Located at: http://wallace.ccfaculty.org/book/book.html. License: CC BY: Attribution