10.5: Exercises

Last updated
Save as PDF

Page ID: 51630

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

List out the elements of the set “The letters of the word Mississippi”
List out the elements of the set “Months of the year”
Write a verbal description of the set {3, 6, 9}
Write a verbal description of the set {a, i, e, o, u}
Is {1, 3, 5} a subset of the set of odd integers?
Is {A, B, C} a subset of the set of letters of the alphabet?

For problems 7-12, consider the sets below, and indicate if each statement is true or false.

A = {1, 2, 3, 4, 5} B = {1, 3, 5} C = {4, 6} U = {numbers from 0 to 10}
3 ∊ B 8. 5 ∊ C
B ⊂ A
C ⊂ A
C ⊂ B
C ⊂ D

Using the sets from above, and treating U as the Universal set, find each of the following:

A ⋃ B
A ⋃ C
A ⋂ C
B ⋂ C
Ac
Bc

Let D = {b, a, c, k}, E = {t, a, s, k}, F = {b, a, t, h}. Using these sets, find the following:

Dc ⋂ E
Fc ⋂ D
(D ⋂ E) ⋃ F
D ⋂ (E ⋃ F)
(F ⋂ E)c ⋂ D
(D ⋃ E)c ⋂ F

Create a Venn diagram to illustrate each of the following:

(F ⋂ E) ⋃ D
(D ⋃ E)c ⋂ F
(F c ⋂ E c) ⋂ D
(D ⋃ E) ⋃ F

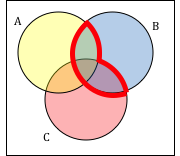
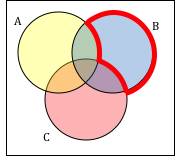
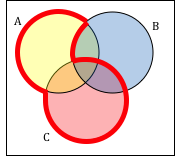
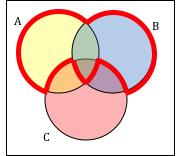
Write an expression for the shaded region.

$abc1$
$abc2$
$abc3$
$abc4$

Let A = {1, 2, 3, 4, 5} B = {1, 3, 5} C = {4, 6}. Find the cardinality of the given set.

n(A)
n(B)
n(A ⋃ C)
n(A ⋂ C)

The Venn diagram here shows the cardinality of each set. Use this in 37-40 to find the cardinality of given set.

n(A ⋂ C)
n(B ⋃ C)
n(A ⋂ B ⋂ Cc)
n(A ⋂ Bc ⋂ C)
If n(G) = 20, n(H) = 30, n(G ⋂ H) = 5, find n(G ⋃ H)
If n(G) = 5, n(H) = 8, n(G ⋂ H) = 4, find n(G ⋃ H)
A survey was given asking whether they watch movies at home from Netflix, Redbox, or a video store. Use the results to determine how many people use Redbox.
52 only use Netflix                             62 only use Redbox
24 only use a video store                    16 use only a video store and Redbox
48 use only Netflix and Redbox          30 use only a video store and Netflix
10 use all three                                    25 use none of these
A survey asked buyers whether color, size, or brand influenced their choice of cell phone. The results are below. How many people were influenced by brand?
5 only said color                     8 only said size
16 only said brand                  20 said only color and size
42 said only color and brand   53 said only size and brand
102 said all three                     20 said none of these
Use the given information to complete a Venn diagram, then determine: a) how many students have seen exactly one of these movies, and b) how many had seen only Star Wars.
18 had seen The Matrix           (M)                  24 had seen Star Wars (SW)
20 had seen Lord of the Rings (LotR)             10 had seen M and SW
14 had seen LotR and SW                                12 had seen M and LotR
6 had seen all three
A survey asked people what alternative transportation modes they use. Using the data to complete a Venn diagram, then determine: a) what percent of people only ride the bus, and b) how many people don’t use any alternate transportation.
30% use the bus                                  20% ride a bicycle
25% walk                                            5% use the bus and ride a bicycle
10% ride a bicycle and walk               12% use the bus and walk
2% use all three

Math in Society. Authored by: Open Textbook Store, Transition Math Project, and the Open Course Library. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY-SA: Attribution-ShareAlike

Search

Text Color

Text Size

Margin Size

Font Type