12.1: Vectors in the Plane
- Last updated
- Save as PDF
- Page ID
- 20183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe a plane vector, using correct notation.
- Perform basic vector operations (scalar multiplication, addition, subtraction).
- Express a vector in component form.
- Explain the formula for the magnitude of a vector.
- Express a vector in terms of unit vectors.
- Give two examples of vector quantities.
When describing the movement of an airplane in flight, it is important to communicate two pieces of information: the direction in which the plane is traveling and the plane’s speed. When measuring a force, such as the thrust of the plane’s engines, it is important to describe not only the strength of that force, but also the direction in which it is applied. Some quantities, such as or force, are defined in terms of both size (also called magnitude) and direction. A quantity that has magnitude and direction is called a vector. In textbooks, vectors are often denoted by boldface letters, such as \(\mathbf{v}\). Since it is difficult to write in clear boldface when we write vectors by hand, we will also include an arrow or harpoon above the letter representing the vector. To make the vectors clearer in this textbook (and to reinforce the way you should write them by hand), we will generally use arrows or harpoons above boldface (or italic) letters to represent vectors, giving us \(\vec v\) or \(\vecs{v}\). Note that some figures will still only use boldface letters to denote vectors.
Definition: Vector
A vector is a quantity that has both magnitude and direction.
Vector Representation
A vector in a plane is represented by a directed line segment (an arrow). The endpoints of the segment are called the initial point and the terminal point of the vector. An arrow from the initial point to the terminal point indicates the direction of the vector. The length of the line segment represents its magnitude. We use the notation \(\|\vecs{v}\|\) to denote the magnitude of the vector \(\vecs{v}\). A vector with an initial point and terminal point that are the same is called the zero vector, denoted \(\vecs{0}\). The zero vector is the only vector without a direction, and by convention can be considered to have any direction convenient to the problem at hand.
Vectors with the same magnitude and direction are called equivalent vectors. We treat equivalent vectors as equal, even if they have different initial points. Thus, if \(\vecs{v}\) and \(\vecs{w}\) are equivalent, we write
\[\vecs{v}=\vecs{w}.\]
Definition: Equivalent Vectors
Vectors are said to be equivalent vectors if they have the same magnitude and direction.
The arrows in Figure \(\PageIndex{1 (b)}\) are equivalent. Each arrow has the same length and direction. A closely related concept is the idea of parallel vectors. Two vectors are said to be parallel if they have the same or opposite directions. We explore this idea in more detail later in the chapter. A vector is defined by its magnitude and direction, regardless of where its initial point is located.
The use of boldface, lowercase letters to name vectors is a common representation in print, but there are alternative notations. When writing the name of a vector by hand, for example, it is easier to sketch an arrow over the variable than to show it is a vector: \(\vec{v}\). When a vector has initial point \(P\) and terminal point \(Q\), the notation \(\vecd{PQ}\) is useful because it indicates the direction and location of the vector.
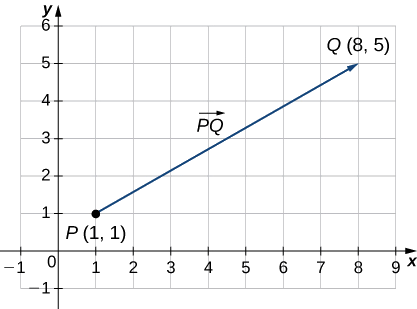
Example \(\PageIndex{1}\): Sketching Vectors
Sketch a vector in the plane from initial point \(P(1,1)\) to terminal point \(Q(8,5)\).
Solution
See Figure \(\PageIndex{2}\). Because the vector goes from point \(P\) to point \(Q\), we name it \(\vecd{PQ}\).
Exercise \(\PageIndex{1}\)
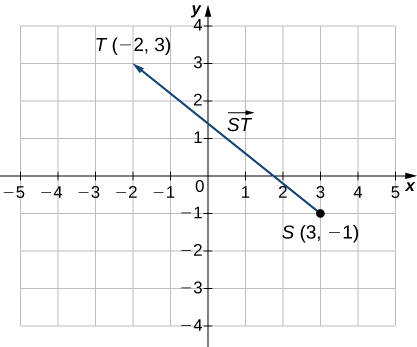
Sketch the vector \(\vecd{ST}\) where \(S\) is point \((3,−1)\) and \(T\) is point \((−2,3).\)
- Hint
-
The first point listed in the name of the vector is the initial point of the vector.
- Answer
-
Combining Vectors
Vectors have many real-life applications, including situations involving force or velocity. For example, consider the forces acting on a boat crossing a river. The boat’s motor generates a force in one direction, and the current of the river generates a force in another direction. Both forces are vectors. We must take both the magnitude and direction of each force into account if we want to know where the boat will go.
A second example that involves vectors is a quarterback throwing a football. The quarterback does not throw the ball parallel to the ground; instead, he aims up into the air. The velocity of his throw can be represented by a vector. If we know how hard he throws the ball (magnitude—in this case, speed), and the angle (direction), we can tell how far the ball will travel down the field.
A real number is often called a scalar in mathematics and physics. Unlike vectors, scalars are generally considered to have a magnitude only, but no direction. Multiplying a vector by a scalar changes the vector’s magnitude. This is called scalar multiplication. Note that changing the magnitude of a vector does not indicate a change in its direction. For example, wind blowing from north to south might increase or decrease in speed while maintaining its direction from north to south.
Definition: Scalar Multiplication
The product \(k\vecs{v}\) of a vector \(\vecs{v}\) and a scalar \(k\) is a vector with a magnitude that is \(|k|\) times the magnitude of \(\vecs{v}\), and with a direction that is the same as the direction of \(\vecs{v}\) if \(k>0\), and opposite the direction of \(\vecs{v}\) if \(k<0\). This is called scalar multiplication. If \(k=0\) or \(\vecs{v}=\vecs{0}\), then \(k\vecs{v}=\vecs{0}.\)
As you might expect, if \(k=−1\), we denote the product \(k\vecs{v}\) as
\[k\vecs{v}=(−1)\vecs{v}=−\vecs{v}.\]
Note that \(−\vecs{v}\) has the same magnitude as \(\vecs{v}\), but has the opposite direction (Figure \(\PageIndex{3}\)).
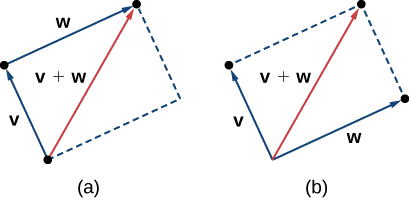
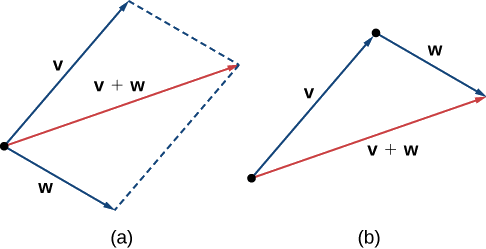
Another operation we can perform on vectors is to add them together in vector addition, but because each vector may have its own direction, the process is different from adding two numbers. The most common graphical method for adding two vectors is to place the initial point of the second vector at the terminal point of the first, as in Figure \(\PageIndex{4 (a)}\). To see why this makes sense, suppose, for example, that both vectors represent displacement. If an object moves first from the initial point to the terminal point of vector \(\vecs{v}\), then from the initial point to the terminal point of vector \(\vecs{w}\), the overall displacement is the same as if the object had made just one movement from the initial point to the terminal point of the vector \(\vecs{v}+\vecs{w}\). For obvious reasons, this approach is called the triangle method. Notice that if we had switched the order, so that \(\vecs{w}\) was our first vector and \(\vecs{v}\) was our second vector, we would have ended up in the same place. (Again, see Figure \(\PageIndex{4 (a)}\).) Thus,
\[ \vecs{v}+ \vecs{w}= \vecs{w}+ \vecs{v}.\]
A second method for adding vectors is called the parallelogram method. With this method, we place the two vectors so they have the same initial point, and then we draw a parallelogram with the vectors as two adjacent sides, as in Figure \(\PageIndex{4 (b)}\). The length of the diagonal of the parallelogram is the sum. Comparing Figure \(\PageIndex{4 (b)}\) and Figure \(\PageIndex{4 (a)}\), we can see that we get the same answer using either method. The vector \( \vecs{v}+ \vecs{w}\) is called the vector sum.
Definition: Vector Addition
The sum of two vectors \(\vecs{v}\) and \(\vecs{w}\) can be constructed graphically by placing the initial point of \(\vecs{w}\) at the terminal point of \(\vecs{v}\). Then, the vector sum, \(\vecs{v}+\vecs{w}\), is the vector with an initial point that coincides with the initial point of \(\vecs{v}\) and has a terminal point that coincides with the terminal point of \(\vecs{w}\). This operation is known as vector addition.
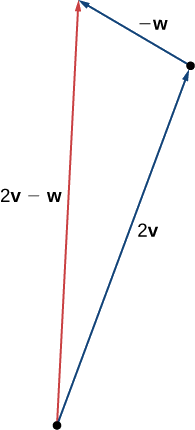
It is also appropriate here to discuss vector subtraction. We define \(\vecs{v}−\vecs{w}\) as \(\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\). The vector \(\vecs{v}−\vecs{w}\) is called the vector difference. Graphically, the vector \(\vecs{v}−\vecs{w}\) is depicted by drawing a vector from the terminal point of \(\vecs{w}\) to the terminal point of \(\vecs{v}\) (Figure \(\PageIndex{5}\)).
In Figure \(\PageIndex{4 (a)}\), the initial point of \(\vecs{v}+\vecs{w}\) is the initial point of \(\vecs{v}\). The terminal point of \(\vecs{v}+\vecs{w}\) is the terminal point of \(\vecs{w}\). These three vectors form the sides of a triangle. It follows that the length of any one side is less than the sum of the lengths of the remaining sides. So we have
\[\|\vecs{v}+\vecs{w}\|≤\|\vecs{v}\|+\|\vecs{w}\|.\]
This is known more generally as the triangle inequality. There is one case, however, when the resultant vector \(\vecs{u}+\vecs{v}\) has the same magnitude as the sum of the magnitudes of \(\vecs{u}\) and \(\vecs{v}\). This happens only when \(\vecs{u}\) and \(\vecs{v}\) have the same direction.
Example \(\PageIndex{2}\): Combining Vectors
Given the vectors \(\vecs v\) and \(\vecs w\) shown in Figure \(\PageIndex{6}\), sketch the vectors
- \(3\vecs{w}\)
- \(\vecs{v}+\vecs{w}\)
- \(2\vecs{v}−\vecs{w}\)
Solution
a. The vector \(3\vecs{w}\) has the same direction as \(\vecs{w}\); it is three times as long as \(\vecs{w}\).
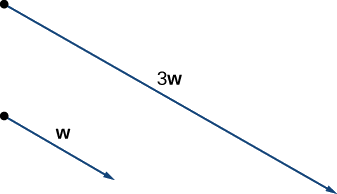
Vector \(3\vecs{w}\) has the same direction as \(\vecs{w}\) and is three times as long.
b. Use either addition method to find \(\vecs{v}+\vecs{w}\).
c. To find \(2\vecs{v}−\vecs{w}\), we can first rewrite the expression as \(2\vecs{v}+(−\vecs{w})\). Then we can draw the vector \(−\vecs{w}\), then add it to the vector \(2\vecs{v}\).
Exercise \(\PageIndex{2}\)
Using vectors \(\vecs{v}\) and \(\vecs{w}\) from Example \(\PageIndex{2}\), sketch the vector \(2\vecs{w}−\vecs{v}\).
- Hint
-
First sketch vectors \(2\vecs{w}\) and \(−\vecs{v}\).
- Answer
-
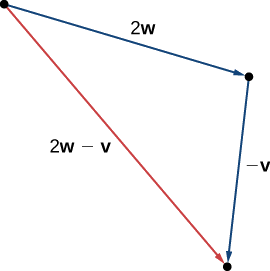
Vector Components
Working with vectors in a plane is easier when we are working in a coordinate system. When the initial points and terminal points of vectors are given in Cartesian coordinates, computations become straightforward.
Example \(\PageIndex{3}\): Comparing Vectors
Are \(\vecs{v}\) and \(\vecs{w}\) equivalent vectors?
a.
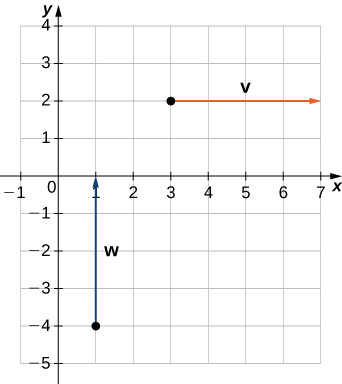
- \(\vecs{v}\) has initial point \((3,2)\) and terminal point \((7,2)\)
- \(\vecs{w}\) has initial point \((1,−4)\) and terminal point \((1,0)\)
b.
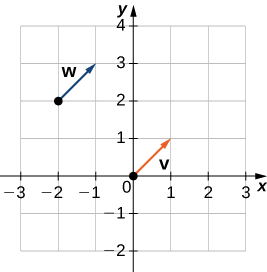
- \(\vecs{v}\) has initial point \((0,0)\) and terminal point \((1,1)\)
- \(\vecs{w}\) has initial point \((−2,2)\) and terminal point \((−1,3)\)
Solution
a. The vectors are each \(4\) units long, but they are oriented in different directions. So \(\vecs{v}\) and \(\vecs{w}\) are not equivalent (Figure \(\PageIndex{9}\)).
b. Based on Figure \(\PageIndex{10}\), and using a bit of geometry, it is clear these vectors have the same length and the same direction, so \(\vecs{v}\) and \(\vecs{w}\) are equivalent.
Exercise \(\PageIndex{3}\)
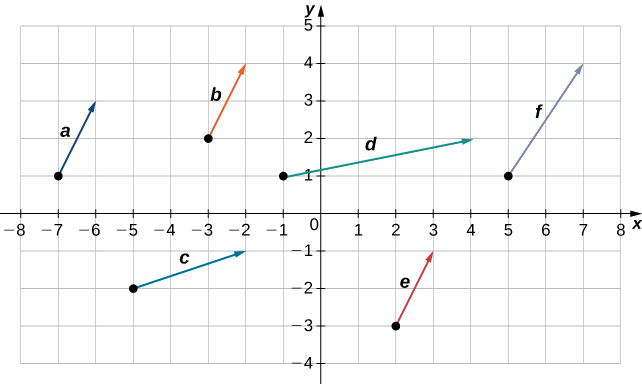
Which of the following vectors are equivalent?
- Hint
-
Equivalent vectors have both the same magnitude and the same direction.
- Answer
-
Vectors \(\vecs{a}, \vecs{b}\), and \(\vecs{e}\) are equivalent.
We have seen how to plot a vector when we are given an initial point and a terminal point. However, because a vector can be placed anywhere in a plane, it may be easier to perform calculations with a vector when its initial point coincides with the origin. We call a vector with its initial point at the origin a standard-position vector. Because the initial point of any vector in standard position is known to be \((0,0)\), we can describe the vector by looking at the coordinates of its terminal point. Thus, if vector \(\vecs{v}\) has its initial point at the origin and its terminal point at \((x,y),\) we write the vector in component form as
\[\vecs{v}=⟨x,y⟩.\]
When a vector is written in component form like this, the scalars x and y are called the components of \(\vecs{v}\).
Definition: Vector components
The vector with initial point \((0,0)\) and terminal point \((x,y)\) can be written in component form as
\[\vecs{v}=⟨x,y⟩.\]
The scalars \(x\) and \(y\) are called the components of \(\vecs{v}\).
Recall that vectors are named with lowercase letters in bold type or by drawing an arrow over their name. We have also learned that we can name a vector by its component form, with the coordinates of its terminal point in angle brackets. However, when writing the component form of a vector, it is important to distinguish between \(⟨x,y⟩\) and \((x,y)\). The first ordered pair uses angle brackets to describe a vector, whereas the second uses parentheses to describe a point in a plane. The initial point of \(⟨x,y⟩\) is \((0,0)\); the terminal point of \(⟨x,y⟩\) is \((x,y)\).
When we have a vector not already in standard position, we can determine its component form in one of two ways. We can use a geometric approach, in which we sketch the vector in the coordinate plane, and then sketch an equivalent standard-position vector. Alternatively, we can find it algebraically, using the coordinates of the initial point and the terminal point. To find it algebraically, we subtract the \(x\)-coordinate of the initial point from the \(x\)-coordinate of the terminal point to get the \(x\)-component, and we subtract the \(y\)-coordinate of the initial point from the \(y\)-coordinate of the terminal point to get the \(y\)-component.
Rule: Component Form of a Vector
Let \(\vecs{v}\) be a vector with initial point \((x_i,y_i)\) and terminal point \((x_t,y_t)\). Then we can express \(\vecs{v}\) in component form as \(\vecs{v}=⟨x_t−x_i,y_t−y_i⟩\).
Example \(\PageIndex{4}\): Expressing Vectors in Component Form
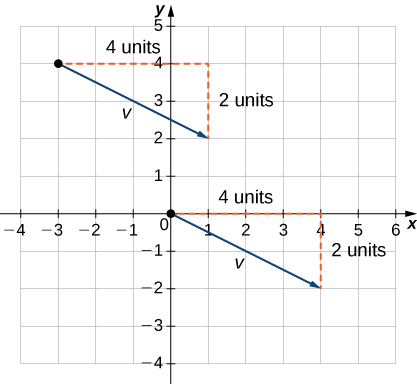
Express vector \(\vecs{v}\) with initial point \((−3,4)\) and terminal point \((1,2)\) in component form.
Solution:
a. Geometric
1. Sketch the vector in the coordinate plane (Figure \(\PageIndex{11}\)).
2. The terminal point is 4 units to the right and 2 units down from the initial point.
3. Find the point that is 4 units to the right and 2 units down from the origin.
4. In standard position, this vector has initial point \((0,0)\) and terminal point \((4,−2)\):
\(\vecs{v}=⟨4,−2⟩.\)
b. Algebraic
In the first solution, we used a sketch of the vector to see that the terminal point lies 4 units to the right. We can accomplish this algebraically by finding the difference of the \(x\)-coordinates:
\(x_t−x_i=1−(−3)=4.\)
Similarly, the difference of the \(y\)-coordinates shows the vertical length of the vector.
\(y_t−y_i=2−4=−2.\)
So, in component form,
\(\vecs{v}=⟨x_t−x_i,y_t−y_i⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩.\)
Exercise \(\PageIndex{4}\)
Vector \(\vecs{w}\) has initial point \((−4,−5)\) and terminal point \((−1,2)\). Express \(\vecs{w}\) in component form.
- Hint
-
You may use either geometric or algebraic method.
- Answer
-
\(⟨3,7⟩\)
To find the magnitude of a vector, we calculate the distance between its initial point and its terminal point. The magnitude of vector \(\vecs{v}=⟨x,y⟩\) is denoted \(\|\vecs{v}\|,\) or \(|\vecs{v}|\), and can be computed using the formula
\[\|\vecs{v}\|=\sqrt{x^2+y^2}.\]
Note that because this vector is written in component form, it is equivalent to a vector in standard position, with its initial point at the origin and terminal point \((x,y)\). Thus, it suffices to calculate the magnitude of the vector in standard position. Using the distance formula to calculate the distance between initial point \((0,0)\) and terminal point \((x,y)\), we have
\[\|\vecs{v}\|=\sqrt{(x−0)^2+(y−0)^2}=\sqrt{x^2+y^2}.\]
Based on this formula, it is clear that for any vector \(\vecs{v}, \|\vecs{v}\|≥0,\) and \(\|\vecs{v}\|=0\) if and only if \(\vecs{v}=\vecs{0}\).
The magnitude of a vector can also be derived using the Pythagorean theorem, as in the following figure.
We have defined scalar multiplication and vector addition geometrically. Expressing vectors in component form allows us to perform these same operations algebraically.
Definition: Scalar multiplication and Vector addition
Let \(\vecs{v}=⟨x_1,y_1⟩\) and \(\vecs{w}=⟨x_2,y_2⟩\) be vectors, and let \(k\) be a scalar.
- Scalar multiplication: \[k\vecs{v}=⟨kx_1,ky_1⟩\]
- Vector addition: \[\vecs{v}+\vecs{w}=⟨x_1,y_1⟩+⟨x_2,y_2⟩=⟨x_1+x_2,y_1+y_2⟩\]
Example \(\PageIndex{5}\): Performing Operations in Component Form
Let \(\vecs{v}\) be the vector with initial point \((2,5)\) and terminal point \((8,13)\), and let \(\vecs{w}=⟨−2,4⟩\).
- Express \(\vecs{v}\) in component form and find \(\|\vecs{v}\|\). Then, using algebra, find
- \(\vecs{v}+\vecs{w}\),
- \(3\vecs{v}\), and
- \(\vecs{v}−2\vecs{w}\).
Solution
a. To place the initial point of \(\vecs{v}\) at the origin, we must translate the vector 2 units to the left and 5 units down (Figure \(\PageIndex{13}\)). Using the algebraic method, we can express \(\vecs{v}\) as \(\vecs{v}=⟨8−2,13−5⟩=⟨6,8⟩\):
\(\|\vecs{v}\|=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10\).
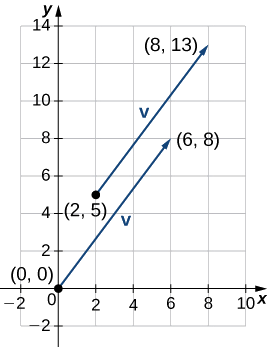
b. To find \(\vecs{v}+\vecs{w}\), add the \(x\)-components and the \(y\)-components separately:
\(\vecs{v}+\vecs{w}=⟨6,8⟩+⟨−2,4⟩=⟨4,12⟩.\)
c. To find \(3\vecs{v}\), multiply \(\vecs{v}\) by the scalar \(k=3\):
\(3\vecs{v}=3⋅⟨6,8⟩=⟨3⋅6,3⋅8⟩=⟨18,24⟩.\)
d. To find \(\vecs{v}−2\vecs{w}\), find \(−2\vecs{w}\) and add it to \(\vecs{v}:\)
\(\vecs{v}−2\vecs{w}=⟨6,8⟩−2⋅⟨−2,4⟩=⟨6,8⟩+⟨4,−8⟩=⟨10,0⟩.\)
Exercise \(\PageIndex{5A}\)
Let \(\vecs{a}=⟨7,1⟩\) and let \(\vecs{b}\) be the vector with initial point \((3,2)\) and terminal point \((−1,−1).\)
- Find \(\|\vecs{a}\|\).
- Express \(\vecs{b}\) in component form.
- Find \(3\vecs{a}−4\vecs{b}.\)
- Hint
-
Use the Pythagorean Theorem to find \(\|\vecs{a}\|\). To find \(3\vecs{a}−4\vecs{b}\), start by finding the scalar multiples \(3\vecs{a}\) and \(−4\vecs{b}\).
- Answer a
-
\(\|\vecs{a}\|=5\sqrt{2},\)
- Answer b
-
\(\vecs{b}=⟨−4,−3⟩,\)
- Answer c
-
\(3\vecs{a}−4\vecs{b}=⟨37,15⟩\)
Now that we have established the basic rules of vector arithmetic, we can state the properties of vector operations. We will prove two of these properties. The others can be proved in a similar manner.
Properties of Vector Operations
Let \(\vecs{u}, \, \vecs{v}\), and \(\vecs{w}\) be vectors in a plane. Let \(r\) and \(s\) be scalars.
- Commutative property \[\vecs{u}+\vecs{v}=\vecs{v}+\vecs{u} \label{commutative}\]
- Associative property \[(\vecs{u}+\vecs{v})+\vecs{w}=\vecs{u}+(\vecs{v}+\vecs{w})\]
- Additive identity property \[\vecs{u}+\vecs{0}=\vecs{u}\]
- Additive inverse property \[\vecs{u}+(−\vecs{u})=\vecs{0}\]
- Associativity of scalar multiplication \[r(s\vecs{u})=(rs)\vecs{u}\]
- Distributive property \[(r+s)\vecs{u}=r\vecs{u}+s\vecs{u} \label{Distributive}\]
- Distributive property \[r(\vecs{u}+\vecs{v})=r\vecs{u}+r\vecs{v}\]
- Identity and zero properties \[1\vecs{u}=\vecs{u}, \, 0\vecs{u}=\vecs{0}\]
Proof of Commutative Property
Let \(\vecs{u}=⟨x_1,y_1⟩\) and \(\vecs{v}=⟨x_2,y_2⟩.\) Apply the commutative property (Equation \ref{commutative}) for real numbers:
\[ \begin{align*} \vecs{u}+\vecs{v} =⟨x_1+x_2,y_1+y_2⟩ \\[4pt] = ⟨x_2+x_1,y_2+y_1⟩ \\[4pt] = \vecs{v}+\vecs{u}. \end{align*}\]
□
Proof of Distributive Property
Apply the distributive property (Equation \ref{Distributive}) for real numbers:
\[ \begin{align*} r(\vecs{u}+\vecs{v}) =r⋅⟨x_1+x_2,y_1+y_2⟩ \\[4pt] =⟨r(x_1+x_2),r(y_1+y_2)⟩ \\[4pt] = ⟨rx_1+rx_2,ry_1+ry_2⟩ \\[4pt] = ⟨rx_1,ry_1⟩+⟨rx_2,ry_2⟩ \\[4pt] = r\vecs{u}+r\vecs{v}. \end{align*}\]
□
Exercise \(\PageIndex{5B}\)
Prove the additive inverse property.
- Hint
-
Use the component form of the vectors.
We have found the components of a vector given its initial and terminal points. In some cases, we may only have the magnitude and direction of a vector, not the points. For these vectors, we can identify the horizontal and vertical components using trigonometry (Figure \(\PageIndex{14}\)).
Consider the angle \(θ\) formed by the vector \(\vecs{v}\) and the positive \(x\)-axis. We can see from the triangle that the components of vector \(\vecs{v}\) are \(⟨\|\vecs{v}\| \cos{θ}, \, \|\vecs{v}\| \sin {θ}⟩\). Therefore, given an angle and the magnitude of a vector, we can use the cosine and sine of the angle to find the components of the vector.
Example \(\PageIndex{6}\): Finding the Component Form of a Vector Using Trigonometry
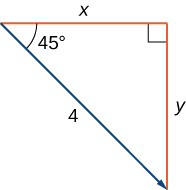
Find the component form of a vector with magnitude 4 that forms an angle of \(−45°\) with the \(x\)-axis.
Solution
Let \(x\) and \(y\) represent the components of the vector (Figure \(\PageIndex{15}\)). Then \(x=4 \cos(−45°)=2 \sqrt{2}\) and \(y=4 \sin(−45°)=−2\sqrt{2}\). The component form of the vector is \(⟨2\sqrt{2},−2\sqrt{2}⟩\).
Exercise \(\PageIndex{6}\)
Find the component form of vector \(\vecs{v}\) with magnitude 10 that forms an angle of \(120°\) with the positive \(x\)-axis.
- Hint
-
\(x=\|\vecs{v}\| \cos θ\) and \(y=\|\vecs{v}\| \sin θ\)
- Answer
-
\(\vecs v=⟨−5,5\sqrt{3}⟩\)
Unit Vectors
A unit vector is a vector with magnitude \(1\). For any nonzero vector \(\vecs{v}\), we can use scalar multiplication to find a unit vector \(\vecs{u}\) that has the same direction as \(\vecs{v}\). To do this, we multiply the vector by the reciprocal of its magnitude:
\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|} \vecs{v}.\]
Recall that when we defined scalar multiplication, we noted that \(\|k\vecs{v}\| =|k|⋅\|\vecs{v}\| \). For \(\vecs{u}=\dfrac{1}{\|\vecs{v}\| }\vecs{v}\), it follows that \(\|\vecs{u}\| =\dfrac{1}{\|\vecs{v}\| }(\|\vecs{v}\| )=1\). We say that \(\vecs{u}\) is the unit vector in the direction of \(\vecs{v}\) (Figure \(\PageIndex{16}\)). The process of using scalar multiplication to find a unit vector with a given direction is called normalization.
Example \(\PageIndex{7}\): Finding a Unit Vector
Let \(\vecs{v}=⟨1,2⟩\).
- Find a unit vector with the same direction as \(\vecs{v}\).
- Find a vector \(\vecs{w}\) with the same direction as \(\vecs{v}\) such that \(\|\vecs{w}\|=7\).
Solution:
a. First, find the magnitude of \(\vecs{v}\), then divide the components of \(\vecs{v}\) by the magnitude:
\[\|\vecs{v}\|=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5} \nonumber\]
\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs v=\dfrac{1}{\sqrt{5}}⟨1,2⟩=\left\langle\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}\right\rangle = \left\langle\dfrac{\sqrt{5}}{5}, \dfrac{2\sqrt{5}}{5}\right\rangle \nonumber.\]
b. The vector \(\vecs{u}\) is in the same direction as \(\vecs{v}\) and \(\|\vecs{u}\|=1\). Use scalar multiplication to increase the length of \(\vecs{u}\) without changing direction:
\[\vecs{w}=7\vecs{u}=7\left\langle\dfrac{\sqrt{5}}{5}, \dfrac{2\sqrt{5}}{5}\right\rangle=\left\langle\dfrac{7\sqrt{5}}{5},\dfrac{14\sqrt{5}}{5}\right\rangle \nonumber.\]
Exercise \(\PageIndex{7}\)
Let \(\vecs{v}=⟨9,2⟩\). Find a vector with magnitude \(5\) in the opposite direction as \(\vecs{v}\).
- Hint
-
First, find a unit vector in the same direction as \(\vecs{v}\).
- Answer
-
\(⟨−\dfrac{45}{\sqrt{85}},−\dfrac{10}{\sqrt{85}}⟩\)
We have seen how convenient it can be to write a vector in component form. Sometimes, though, it is more convenient to write a vector as a sum of a horizontal vector and a vertical vector. To make this easier, let’s look at standard unit vectors. The standard unit vectors are the vectors \(\hat{\mathbf i}=⟨1,0⟩\) and \(\hat{\mathbf j}=⟨0,1⟩\) (Figure \(\PageIndex{17}\)).
By applying the properties of vectors, it is possible to express any vector in terms of \(\hat{\mathbf i}\) and \(\hat{\mathbf j}\) in what we call a linear combination:
\[\vecs{v}=⟨x,y⟩=⟨x,0⟩+⟨0,y⟩=x⟨1,0⟩+y⟨0,1⟩=x\hat{\mathbf i}+y\hat{\mathbf j}.\]
Thus, \(\vecs{v}\) is the sum of a horizontal vector with magnitude \(x\), and a vertical vector with magnitude \(y\), as in Figure \(\PageIndex{18}\).
Figure \(\PageIndex{18}\): The vector \(\vecs{v}\) is the sum of \(x\hat{\mathbf i}\) and \(y\hat{\mathbf j}\).
Now consider Figure \(\PageIndex{19}\) below.
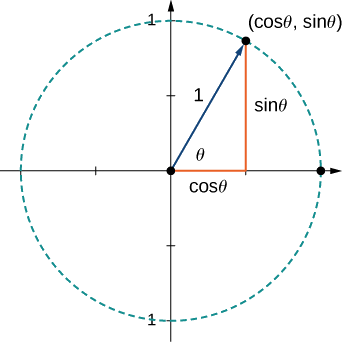
Note that since every vector in standard position (with its initial point at the origin) and with its terminal point on the unit circle is a unit vector! And given any angle \(θ\) with the positive \(x\)-axis, we already know the coordinates of the terminal point are \((\cos θ, \sin θ)\). This gives us an easy way to determine a unit vector in any given direction! The blue unit vector shown in Figure \(\PageIndex{19}\) above will be:
\(\vecs u = <\cos θ, \sin θ>\) or \(\vecs u = \cos θ\,\mathbf{\hat i} + \sin θ \,\mathbf{\hat j}.\)
If we want to scale one of these unit vectors to obtain a vector of a given length \(c\) at a given angle \(θ\) with the positive \(x\)-axis, we can just scale the unit vector by multiplying it by the scalar \(c.\) That is,
\(\vecs v = c\vecs u = c(\cos θ\,\mathbf{\hat i} + \sin θ \,\mathbf{\hat j}) = c\cos θ\,\mathbf{\hat i} + c\sin θ \,\mathbf{\hat j}.\)
Example \(\PageIndex{8}\): Using Standard Unit Vectors
- Express the vector \(\vecs{w}=⟨3,−4⟩\) in terms of standard unit vectors.
- Vector \(\vecs{u}\) is a unit vector that forms an angle of \(60°\) with the positive \(x\)-axis. Use standard unit vectors to describe \(\vecs{u}\).
Solution:
a. Resolve vector \(\vecs{w}\) into a vector with a zero \(y\)-component and a vector with a zero \(x\)-component:
\[\vecs{w}=⟨3,−4⟩=3 \hat{\mathbf i}−4 \hat{\mathbf j}. \nonumber\]
b. Because \(\vecs{u}\) is a unit vector, the terminal point lies on the unit circle when the vector is placed in standard position (Figure \(\PageIndex{19}\)).
\[ \begin{align*} \vecs{u} =⟨\cos 60°,\sin 60°⟩ \\[4pt] =\left\langle\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right\rangle \\[4pt] = \dfrac{1}{2} \hat{\mathbf i}+\dfrac{\sqrt{3}}{2} \hat{\mathbf j}. \end{align*}\]
Exercise \(\PageIndex{8}\)
Let \(\vecs{a}=⟨16,−11⟩\) and let \(\vecs{b}\) be a unit vector that forms an angle of \(225°\) with the positive \(x\)-axis. Express \(\vecs{a}\) and \(\vecs{b}\) in terms of the standard unit vectors.
- Hint
-
Use sine and cosine to find the components of \(\vecs{b}\).
- Answer
-
\(\vecs{a}=16 \hat{\mathbf i}−11 \hat{\mathbf j}, \quad \vecs{b}=−\dfrac{\sqrt{2}}{2} \hat{\mathbf i}−\dfrac{\sqrt{2}}{2} \hat{\mathbf j}\)
Example \(\PageIndex{9}\): Using the Unit Circle to Find Vectors of a Given Length and Angle
a. Let \(\vecs u\) be the vector of length 20 that forms an angle of \(150°\) with the positive \(x\)-axis. Express \(\vecs u\) in terms of the standard unit vectors.
b. Find the vector \(\vecs v\) that has a magnitude of 4 and makes an angle of \(\tfrac{\pi}{3}\) with the positive \(x\)-axis.
Solution
a. First we use the unit circle to write a unit vector making the given angle with the positive \(x\)-axis.
\[\vecs w = \cos 150° \,\hat{\mathbf i} + \sin 150° \,\hat{\mathbf j}\nonumber\]
Since we know the exact values of these trigonometric ratios for \(150°,\) we can now write,
\[ \vecs w = -\frac{\sqrt{3}}{2} \,\hat{\mathbf i} + \frac{1}{2} \,\hat{\mathbf j} \nonumber\]
Note: Since we know that \(150°\) is in the 2nd quadrant and it's \(30°\) above the \(x\)-axis there, we know the coordinates of the terminal point of this unit vector on the unit circle are \(\left( -\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\). Since we're in the 2nd quadrant, we know the \(x\)-coordinate (the cosine value) is negative and the \(y\)-coordinate (the sine value) is positive.
Then the vector \(\vecs u\) that we need is just a scaled version of the unit vector \(\vecs w\). That is, \(\vecs u = 20\vecs w.\)
So
\[\begin{align*} \vecs u &= -20\cdot\frac{\sqrt{3}}{2} \,\hat{\mathbf i} + 20\cdot\frac{1}{2} \,\hat{\mathbf j} \\[6pt]
&=-10\sqrt{3} \,\hat{\mathbf i} + 10 \,\hat{\mathbf j} \end{align*}\]
b. Here we just multiply the relevant unit vector by \(4\).
\[\begin{align*} \vecs v &= 4 \cdot \langle\cos \tfrac{\pi}{3}, \sin \tfrac{\pi}{3} \rangle \\[6pt]
&= 4 \left\langle \frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle \\[6pt]
&= \langle 2, 2\sqrt{3}\rangle \\[6pt]
&= 2 \hat{\mathbf i} + 2\sqrt{3} \hat{\mathbf j} \end{align*}\]
Exercise \(\PageIndex{9}\)
Find vector \(\vecs u\) if we know that \(\|\vecs u\| = 12\) and the vector \(\vecs u\) has an angle of \(\tfrac{7\pi}{4}\) with the positive \(x\)-axis.
- Answer
-
\(\vecs u = 12 \langle \cos \tfrac{7\pi}{4}, \sin \tfrac{7\pi}{4} \rangle = 12 \langle \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\rangle = \langle 6\sqrt{2}, -6\sqrt{2} \rangle\)
Finding the Angle a Given Vector Makes with the Positive x-axis
Since we know that any given vector \(\vecs v\) in the \(xy\)-plane can be normalized to find a unit vector in the same direction, it becomes fairly easy to determine the angle between this vector \(\vecs v\) and the positive \(x\)-axis. Once we normalize the vector \(\vecs v\), we know that this unit vector could be placed on the unit circle and can be written in the form:
\[ <\cos θ, \sin θ> = \cos θ \,\hat{\mathbf i} + \sin θ \,\hat{\mathbf j}\nonumber\]
From our work above, we know the unit vector in the same direction as the vector \(\vecs v\) could be written as \(\vecs w = \frac{\vecs v}{\|\vecs v\|}.\)
Let's say this simplifies down to a unit vector with components \(\vecs w = \langle a, b\rangle.\) Since this is a unit vector, we know the first component is equal to \(\cos θ\) and the second component is equal to \(\sin θ,\) where \(θ\) is the angle between this vector and the positive \(x\)-axis.
That is,
\( \cos θ = a \) and \(\sin θ = b.\)
If \(θ\) is in the first quadrant, either term will give us the correct \(θ\) using either \(θ = \arccos a\) or \(θ = \arcsin b.\) If we are in another quadrant (look at the signs of the two components to tell which quadrant it lies in), we need to think more carefully about the angle we obtain to be sure it is in the correct quadrant, making an adjustment as needed or using the other inverse trig function.
Example \(\PageIndex{10}\)
a. Given \(\vecs v = 3 \,\hat{\mathbf i} + 4 \,\hat{\mathbf j},\) find the angle \(θ\) that this vector makes with the positive \(x\)-axis (to the nearest hundredth of a degree).
b. Find the angle \(θ\) between the positive \(x\)-axis and the vector \(\vecs u = <-2, 4>\) (to the nearest thousandth of a radian and to the nearest tenth of a degree).
c. Find the angle \(θ\) between the positive \(x\)-axis and the vector \(\vecs w = 1\,\hat{\mathbf i} - 3 \,\hat{\mathbf j}\) (to the nearest thousandth of a radian and to the nearest tenth of a degree).
Solution
a. Since this vector is in the first quadrant, this one is easiest to work out. First we normalize this vector (find a unit vector in the same direction).
Since \(\|\vecs v\| = \sqrt{3^2 + 4^2} = \sqrt{9+16} = \sqrt{25} = 5,\) we get the unit vector,
\[ \vecs u = \frac{3}{5} \,\hat{\mathbf i} + \frac{4}{5} \,\hat{\mathbf j}.\nonumber\]
Now we can find \(θ\) with either component. That is,
\[ θ = \arccos \frac{3}{5} = \arcsin \frac{4}{5} \approx 53.13°.\nonumber\]
b. The signs of the components of this vector tell us it is in the second quadrant, so we know that the arccosine function will still work for us, as it returns an angle in the first or second quadrants (between \(0\) and \(\pi\) radians). But note that arcsine would not give us the correct angle (right away) since it always returns an angle between \(-\tfrac{\pi}{2}\) and \(\tfrac{\pi}{2},\) (which effectively returns an angle in the first or fourth quadrants). We could still use it here, knowing it would give us an angle in the first quadrant here (since the sign of the second component is positive). Because of the symmetry involved, we would have to subtract the angle we get from \(\pi\) radians to ontain the correct angle in the second quadrant. This is not trivial, as it requires a clear understanding and an ability to visualize the angles, but we'll show how it works below.
First let's normalize this vector.
Since \(\|\vecs u\| = \sqrt{(-2)^2 + 4^2} = \sqrt{4+16} = \sqrt{20} = 2\sqrt{5},\) we get the unit vector,
\[\left\langle \frac{-2}{2\sqrt{5}}, \frac{4}{2\sqrt{5}} \right\rangle = \left\langle -\frac{\sqrt{5}}{5}, \frac{2\sqrt{5}}{5} \right\rangle. \nonumber\]
Now using the first component, we find,
\[ θ = \arccos -\frac{\sqrt{5}}{5} \approx 2.034\text{ radians }\approx 116.6°.\nonumber\]
Note that this angle is indeed in the second quadrant, as it needed to be!
Now let's see what would have happened if we used the second component and the arcsine function.
\[ \arcsin \frac{2\sqrt{5}}{5} \approx 1.1071\text{ radians }\approx 63.4°\nonumber\]
As explained above, since this angle is in the first quadrant, we'll need to subtract it from \(\pi\) radians to get to the correct angle.
So here we get,
\[ θ = \pi - \arcsin \frac{2\sqrt{5}}{5} \approx 3.14159 - 1.1071 \approx 2.034\text{ radians}\nonumber\]
or in degrees,
\[ θ = 180° - \arcsin \frac{2\sqrt{5}}{5} \approx 180° - 63.4 \approx 116.6°.\nonumber\]
We can see that this is the same angle!
c. Since \(\|\vecs w\| = \sqrt{10},\) the unit vector in the same direction as \(\vecs w = 1\,\hat{\mathbf i} - 3 \,\hat{\mathbf j}\) is \(\frac{\sqrt{10}}{10}\,\hat{\mathbf i} - \frac{3\sqrt{10}}{10} \,\hat{\mathbf j}.\) Because this vector is clearly in the fourth quadrant, the arcsine function is our choice.
Here,
\( θ = \arcsin -\frac{3\sqrt{10}}{10} \approx -1.249\) radians \(\approx -71.6°.\)
This is a correct answer, but if we were asked for an angle between \(0\) and \(2\pi\) radians, for example, we would still need to adjust it by adding \(2\pi\) radians to the radian version of the angle. Then \(θ \approx 5.034\) radians.
If the vector is in the third quadrant neither the arccosine nor the arcsine give us the right angle. We could use either one and adjust the angle as we showed with arcsine in Example \(\PageIndex{10}\), part b above. But there is another option. Although it also may need an adjustment, this adjustment is somewhat easier to make.
If we run into difficulty with the approach above or just want to use a different method, we can instead use the arctangent function to find the angle \(θ\) a vector \(\vecs v\) makes with the positive \(x\)-axis. One advantage this approach gives us is that we don't need to normalize the vector first. Since \(\tan θ = \dfrac{\sin θ}{\cos θ},\) this ratio of the two vector components automatically removes any scalar that may be present and gives us the correct tangent ratio.
As we observe in Figure \(\PageIndex{20}\), given a non-zero vector, \(\vecs v = <\|\vecs v\|\cos θ, \|\vecs v\|\sin θ>,\) we know that,
\[\tan θ = \frac{\|\vecs v\|\sin θ}{\|\vecs v\|\cos θ} = \frac{\sin θ}{\cos θ}. \nonumber\]
However, like the arcsine function, the arctangent function only returns angles between \(-\tfrac{\pi}{2}\) and \(\tfrac{\pi}{2},\) so we will still need to adjust the resulting angle based on which quadrant in which we know it must lie. At least in this case, the worst that we will need to do is to add \(\pi\) radians or \(180°\) to our angle to get it into the correct quadrant. [Note that this is because the tangent will give the same results when the signs of the sine and cosine are the same, and it will give the same results when the signs of the two ratios are different.]
Example \(\PageIndex{11}\)
Find the angle \(θ\) between the positive \(x\)-axis and the vector \(\vecs d = <-5, -1>\) (to the nearest thousandth of a radian and to the nearest tenth of a degree).
Solution
The vector \(\vecs d = <-5, -1>\) is clearly in the third quadrant, and will not be given directly by either the arccosine function or the arcsine function, as mentioned above. But we do know that the arctangent function will return an angle in the first quadrant in this situation (the two components are the same sign and thus their ratio is positive), and the correct angle in the third quadrant will be 180° or \(\pi\) radians greater than the angle we are given by arctangent in the first quadrant.
Remembering that we don't need to determine the unit vector this time, we instead write the tangent ratio we will need to work with.
\[\tan θ = \frac{-1}{-5} = \frac{1}{5}\nonumber\]
So,
\(θ = \pi + \arctan \frac{1}{5} \approx \pi + 0.197\) radians \(\approx 3.339\) radians \(\approx 191.3°.\)
Note that in degrees, \(\arctan \frac{1}{5} \approx 11.3°.\) Adding \(180°\) also gives us \(191.3°.\)
Exercise \(\PageIndex{10}\)
Use the arctangent function to determine the angle \(θ\) between the given vector and the positive \(x\)-axis. Give the angle accurate to the nearest tenth of a degree.
a. \(\vecs u = <-4, -8>\)
b. \(\vecs v = <10, -15>\)
c. \(\vecs w = <-7, 1>\)
- Answer
-
a. \(θ \approx 243.4°\)
b. \(θ \approx -56.3° = 303.7°\)
c. \(θ \approx 171.9°\)
Applications of Vectors
Because vectors have both direction and magnitude, they are valuable tools for solving problems involving such applications as motion and force. Recall the boat example and the quarterback example we described earlier. Here we look at two other examples in detail.
Example \(\PageIndex{12A}\): Finding Resultant Force
Jane’s car is stuck in the mud. Lisa and Jed come along in a truck to help pull her out. They attach one end of a tow strap to the front of the car and the other end to the truck’s trailer hitch, and the truck starts to pull. Meanwhile, Jane and Jed get behind the car and push. The truck generates a horizontal force of 300 lb on the car. Jane and Jed are pushing at a slight upward angle and generate a force of 150 lb on the car. These forces can be represented by vectors, as shown in Figure \(\PageIndex{21}\). The angle between these vectors is 15°. Find the resultant force (the vector sum) and give its magnitude to the nearest tenth of a pound and its direction angle from the positive \(x\)-axis.
Solution
To find the effect of combining the two forces, add their representative vectors. First, express each vector in component form or in terms of the standard unit vectors. For this purpose, it is easiest if we align one of the vectors with the positive \(x\)-axis. The horizontal vector, then, has initial point \((0,0)\) and terminal point \((300,0)\). It can be expressed as \(⟨300,0⟩\) or \(300 \hat{\mathbf i}\).
The second vector has magnitude \(150\) and makes an angle of \(15°\) with the first, so we can express it as \(⟨150 \cos(15°),150 \sin(15°)⟩,\) or \(150 \cos(15°)\hat{\mathbf i}+150 \sin(15°)\hat{\mathbf j}\). Then, the sum of the vectors, or resultant vector, is \(\vecs{r}=⟨300,0⟩+⟨150 \cos(15°),150 \sin(15°)⟩,\) and we have
\[\|\vecs{r}\|=\sqrt{(300+150 \cos(15°))^2+(150 \sin(15°))^2}≈446.6. \nonumber\]
The angle \(θ\) made by \(\vecs{r}\) and the positive \(x\)-axis has \(\tan θ=\dfrac{150 \sin 15°}{(300+150\cos 15°)}≈0.09\), so \(θ≈ \tan^{−1}(0.09)≈5°\), which means the resultant force \(\vecs{r}\) has an angle of \(5°\) above the horizontal axis.
Example \(\PageIndex{12B}\): Finding Resultant Velocity
An airplane flies due west at an airspeed of \(425\) mph. The wind is blowing from the northeast at \(40\) mph. What is the ground speed of the airplane? What is the bearing of the airplane?
Solution
Let’s start by sketching the situation described (Figure \(\PageIndex{22}\)).
Set up a sketch so that the initial points of the vectors lie at the origin. Then, the plane’s velocity vector is \(\vecs{p}=−425\hat{\mathbf i}\). The vector describing the wind makes an angle of \(225°\) with the positive \(x\)-axis:
\[\vecs{w}=⟨40 \cos(225°),40 \sin(225°)⟩=\left\langle−\dfrac{40\sqrt{2}}{2},−\dfrac{40\sqrt{2}}{2}\right\rangle=−20\sqrt{2}\,\hat{\mathbf i}−20\sqrt{2}\,\hat{\mathbf j}. \nonumber\]
When the airspeed and the wind act together on the plane, we can add their vectors to find the resultant force:
\[\vecs{p}+\vecs{w}=−425\hat{\mathbf i}+\left(−20\sqrt{2}\,\hat{\mathbf i}−20\sqrt{2}\,\hat{\mathbf j}\right)=\left(−425−20\sqrt{2}\right)\hat{\mathbf i}−20\sqrt{2}\,\hat{\mathbf j}. \nonumber\]
The magnitude of the resultant vector shows the effect of the wind on the ground speed of the airplane:
\(\|\vecs{p}+\vecs{w}\|=\sqrt{\left(−425−20\sqrt{2}\right)^2+\left(−20\sqrt{2}\right)^2}≈454.17\) mph
As a result of the wind, the plane is traveling at approximately \(454\) mph relative to the ground.
To determine the bearing of the airplane, we want to find the direction of the vector \(\vecs{p}+\vecs{w}\):
\(\tan θ=\dfrac{−20\sqrt{2}}{\left(−425−20\sqrt{2}\right)}≈0.06\)
\(θ≈3.57°\).
The overall direction of the plane is \(3.57°\) south of west.
Exercise \(\PageIndex{11}\)
An airplane flies due north at an airspeed of \(550\) mph. The wind is blowing from the northwest at \(50\) mph. What is the ground speed of the airplane?
- Hint
-
Sketch the vectors with the same initial point and find their sum.
- Answer
-
Approximately \(516\) mph
Key Concepts
- Vectors are used to represent quantities that have both magnitude and direction.
- We can add vectors by using the parallelogram method or the triangle method to find the sum. We can multiply a vector by a scalar to change its length or give it the opposite direction.
- Subtraction of vectors is defined in terms of adding the negative of the vector.
- A vector is written in component form as \(\vecs{v}=⟨x,y⟩\).
- The magnitude of a vector is a scalar: \(‖\vecs{v}‖=\sqrt{x^2+y^2}\).
- A unit vector \(\vecs{u}\) has magnitude \(1\) and can be found by dividing a vector by its magnitude: \(\vecs{u}=\dfrac{1}{‖\vecs{v}‖}\vecs{v}\). The standard unit vectors are \(\hat{\mathbf i}=⟨1,0⟩\) and \(\hat{\mathbf j}=⟨0,1⟩\). A vector \(\vecs{v}=⟨x,y⟩\) can be expressed in terms of the standard unit vectors as \(\vecs{v}=x\hat{\mathbf i}+y\hat{\mathbf j}\).
- Vectors are often used in physics and engineering to represent forces and velocities, among other quantities.
Glossary
- component
- a scalar that describes either the vertical or horizontal direction of a vector
- equivalent vectors
- vectors that have the same magnitude and the same direction
- initial point
- the starting point of a vector
- magnitude
- the length of a vector
- normalization
- using scalar multiplication to find a unit vector with a given direction
- parallelogram method
- a method for finding the sum of two vectors; position the vectors so they share the same initial point; the vectors then form two adjacent sides of a parallelogram; the sum of the vectors is the diagonal of that parallelogram
- scalar
- a real number
- scalar multiplication
- a vector operation that defines the product of a scalar and a vector
- standard-position vector
- a vector with initial point \((0,0)\)
- standard unit vectors
- unit vectors along the coordinate axes: \(\hat{\mathbf i}=⟨1,0⟩,\, \hat{\mathbf j}=⟨0,1⟩\)
- terminal point
- the endpoint of a vector
- triangle inequality
- the length of any side of a triangle is less than the sum of the lengths of the other two sides
- triangle method
- a method for finding the sum of two vectors; position the vectors so the terminal point of one vector is the initial point of the other; these vectors then form two sides of a triangle; the sum of the vectors is the vector that forms the third side; the initial point of the sum is the initial point of the first vector; the terminal point of the sum is the terminal point of the second vector
- unit vector
- a vector with magnitude \(1\)
- vector
- a mathematical object that has both magnitude and direction
- vector addition
- a vector operation that defines the sum of two vectors
- vector difference
- the vector difference \(\vecs{v}−\vecs{w}\) is defined as \(\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\)
- vector sum
- the sum of two vectors, \(\vecs{v}\) and \(\vecs{w}\), can be constructed graphically by placing the initial point of \(\vecs{w}\) at the terminal point of \(\vecs{v}\); then the vector sum \(\vecs{v}+\vecs{w}\) is the vector with an initial point that coincides with the initial point of \(\vecs{v}\), and with a terminal point that coincides with the terminal point of \(\vecs{w}\)
- zero vector
- the vector with both initial point and terminal point \((0,0)\)
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Paul Seeburger (Monroe Community College) added exposition below Figure \(\PageIndex{8}\) and above Example \(\PageIndex{8},\) and also added Example \(\PageIndex{9},\) Exercise \(\PageIndex{9},\) and all of the sub-section titled Finding the Angle a Given Vector Makes with the Positive x-axis, ending just before the sub-section titled Applications of Vectors. Paul also simplified the notation in Example \(\PageIndex{12B}\).

