For exercises 1 - 10, consider points \(P(−1,3), \, Q(1,5),\) and \(R(−3,7)\). Determine the requested vectors and express each of them
a. in component form and
b. by using standard unit vectors.
1) \( \vecd{PQ}\)
- Answer
- a. \(\vecd{PQ}=⟨2,2⟩\)
b. \(\vecd{PQ}=2\hat{\mathbf i}+2\hat{\mathbf j}\)
2) \(\vecd{PR}\)
3) \(\vecd{QP}\)
- Answer
- a. \(\vecd{QP}=⟨−2,−2⟩\)
b. \(\vecd{QP}=−2\hat{\mathbf i}−2\hat{\mathbf j}\)
4) \(\vecd{RP}\)
5) \(\vecd{PQ}+\vecd{PR}\)
- Answer
- a. \(\vecd{PQ}+\vecd{PR}=⟨0,6⟩\)
b. \(\vecd{PQ}+\vecd{PR}=6\hat{\mathbf j}\)
6) \(\vecd{PQ}−\vecd{PR}\)
7) \(2\vecd{PQ}−2\vecd{PR}\)
- Answer
- a. \(2\vecd{PQ}→−2\vecd{PR}=⟨8,−4⟩\)
b. \(2\vecd{PQ}−2\vecd{PR}=8\hat{\mathbf i}−4\hat{\mathbf j}\)
8) \(2\vecd{PQ}+\frac{1}{2}\vecd{PR}\)
9) The unit vector in the direction of \(\vecd{PQ}\)
- Answer
- a. \(\left\langle\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right\rangle\)
b. \(\frac{\sqrt{2}}{2}\hat{\mathbf i}+\frac{\sqrt{2}}{2}\hat{\mathbf j}\)
10) The unit vector in the direction of \(\vecd{PR}\)
11) A vector \({\overset{\scriptstyle\rightharpoonup}{\mathbf v}}\) has initial point \((−1,−3)\) and terminal point \((2,1)\). Find the unit vector in the direction of \(\vecs v\). Express the answer in component form.
- Answer
- \(⟨\frac{3}{5},\frac{4}{5}⟩\)
12) A vector \(\vecs v\) has initial point \((−2,5)\) and terminal point \((3,−1)\). Find the unit vector in the direction of \(\vecs v\). Express the answer in component form.
13) The vector \(\vecs v\) has initial point \(P(1,0)\) and terminal point \(Q\) that is on the \(y\)-axis and above the initial point. Find the coordinates of terminal point \(Q\) such that the magnitude of the vector \(\vecs v\) is \(\sqrt{5}\).
- Answer
- \(Q(0,2)\)
14) The vector \(\vecs v\) has initial point \(P(1,1)\) and terminal point \(Q\) that is on the \(x\)-axis and left of the initial point. Find the coordinates of terminal point \(Q\) such that the magnitude of the vector \(\vecs v\) is \(\sqrt{10}\).
For exercises 15 and 16, use the given vectors \(\vecs a\) and \(\vecs b\).
a. Determine the vector sum \(\vecs a+\vecs b\) and express it in both the component form and by using the standard unit vectors.
b. Find the vector difference \(\vecs a −\vecs b\) and express it in both the component form and by using the standard unit vectors.
c. Verify that the vectors \(\vecs a, \; \vecs b,\) and \(\vecs a+\vecs b\), and, respectively, \(\vecs a, \, \vecs b\), and \(\vecs a−\vecs b\) satisfy the triangle inequality.
d. Determine the vectors \(2\vecs a, \;−\vecs b,\) and \(2\vecs a−\vecs b.\) Express the vectors in both the component form and by using standard unit vectors.
15) \(\vecs a=2\hat{\mathbf i}+\hat{\mathbf j}, \quad \vecs b=\hat{\mathbf i}+3\hat{\mathbf j}\)
- Answer
- \(a.\, \vecs a+\vecs b=⟨3,4⟩, \quad \vecs a+\vecs b=3\hat{\mathbf i}+4\hat{\mathbf j}\)
\(b.\, \vecs a−\vecs b=⟨1,−2⟩, \quad \vecs a−\vecs b=\hat{\mathbf i}−2\hat{\mathbf j}\)
\(c.\) Answers will vary
\(d.\, 2\vecs a=⟨4,2⟩, \quad 2\vecs a=4\hat{\mathbf i}+2\hat{\mathbf j}, \quad −\vecs b=⟨−1,−3⟩, \quad −\vecs b=−\hat{\mathbf i}−3\hat{\mathbf j}, \quad 2\vecs a−\vecs b=⟨3,−1⟩, \quad 2\vecs a−\vecs b=3\hat{\mathbf i}−\hat{\mathbf j}\)
16) \(\vecs a=2\hat{\mathbf i}, \quad \vecs b=−2\hat{\mathbf i}+2\hat{\mathbf j}\)
17) Let \(\vecs a\) be a standard-position vector with terminal point \((−2,−4)\). Let \(\vecs b\) be a vector with initial point \((1,2)\) and terminal point \((−1,4)\). Find the magnitude of vector \(−3\vecs a+\vecs b−4\hat{\mathbf i}+\hat{\mathbf j}.\)
- Answer
- \(15\)
18) Let \(\vecs a\) be a standard-position vector with terminal point at \((2,5)\). Let \(\vecs b\) be a vector with initial point \((−1,3)\) and terminal point \((1,0)\). Find the magnitude of vector \(\vecs a−3\vecs b+14\hat{\mathbf i}−14\hat{\mathbf j}.\)
19) Let \(\vecs u\) and \(\vecs v\) be two nonzero vectors that are nonequivalent. Consider the vectors \(\vecs a=4\vecs u+5\vecs v\) and \(\vecs b=\vecs u+2\vecs v\) defined in terms of \(\vecs u\) and \(\vecs v\). Find the scalar \(λ\) such that vectors \(\vecs a+λ\vecs b\) and \(\vecs u−\vecs v\) are equivalent.
- Answer
- \(λ=−3\)
20) Let \(\vecs u\) and \(\vecs v\) be two nonzero vectors that are nonequivalent. Consider the vectors \(\vecs a=2\vecs u−4\vecs v\) and \(\vecs b=3\vecs u−7\vecs v\) defined in terms of \(\vecs u\) and \(\vecs v\). Find the scalars \(α\) and \(β\) such that vectors \(α\vecs a+β\vecs b\) and \(\vecs u−\vecs v\) are equivalent.
21) Consider the vector \(\vecs a(t)=⟨\cos t, \sin t⟩\) with components that depend on a real number \(t\). As the number \(t\) varies, the components of \(\vecs a(t)\) change as well, depending on the functions that define them.
a. Write the vectors \(\vecs a(0)\) and \(\vecs a(π)\) in component form.
b. Show that the magnitude \(∥\vecs a(t)∥\) of vector \(\vecs a(t)\) remains constant for any real number \(t\).
c. As \(t\) varies, show that the terminal point of vector \(\vecs a(t)\) describes a circle centered at the origin of radius \(1\).
- Answer
- \(a.\, \vecs a(0)=⟨1,0⟩, \quad \vecs a(π)=⟨−1,0⟩\)
\(b.\) Answers may vary
\(c.\) Answers may vary
22) Consider vector \(\vecs a(x)=⟨x,\sqrt{1−x^2}⟩\) with components that depend on a real number \(x∈[−1,1]\). As the number \(x\) varies, the components of \(\vecs a(x)\) change as well, depending on the functions that define them.
a. Write the vectors \(\vecs a(0)\) and \(\vecs a(1)\) in component form.
b. Show that the magnitude \(∥\vecs a(x)∥\) of vector \(\vecs a(x)\) remains constant for any real number \(x\).
c. As \(x\) varies, show that the terminal point of vector \(\vecs a(x)\) describes a circle centered at the origin of radius \(1\).
23) Show that vectors \(\vecs a(t)=⟨\cos t, \sin t⟩\) and \(\vecs a(x)=⟨x,\sqrt{1−x^2}⟩\) are equivalent for \(x=1\) and \(t=2kπ\), where \(k\) is an integer.
Answer Answers may vary
24) Show that vectors \(\vecs a(t)=⟨\cos t, \sin t⟩\) and \(\vecs a(x)=⟨x,\sqrt{1−x^2}⟩\) are opposite for \(x=1\) and \(t=π+2kπ\), where \(k\) is an integer.
For exercises 25-28, find a vector \(\vecs v\) with the given magnitude and in the same direction as the vector \(\vecs u\).
25) \(\|\vecs v\|=7, \quad \vecs u=⟨3,4⟩\)
- Answer
- \(\vecs v=⟨\frac{21}{5},\frac{28}{5}⟩\)
26) \(‖\vecs v‖=3,\quad \vecs u=⟨−2,5⟩\)
27) \(‖\vecs v‖=7,\quad \vecs u=⟨3,−5⟩\)
- Answer
- \(\vecs v=⟨\frac{21\sqrt{34}}{34},−\frac{35\sqrt{34}}{34}⟩\)
28) \(‖\vecs v‖=10,\quad \vecs u=⟨2,−1⟩\)
For exercises 29-34, find the component form of vector \(\vecs u\), given its magnitude and the angle the vector makes with the positive \(x\)-axis. Give exact answers when possible.
29) \(‖\vecs u‖=2, θ=30°\)
- Answer
- \(\vecs u=⟨\sqrt{3},1⟩\)
30) \(‖\vecs u‖=6, θ=60°\)
31) \(‖\vecs u‖=5, θ=\frac{π}{2}\)
- Answer
- \(\vecs u=⟨0,5⟩\)
32) \(‖\vecs u‖=8, θ=π\)
33) \(‖\vecs u‖=10, θ=\frac{5π}{6}\)
- Answer
- \(\vecs u=⟨−5\sqrt{3},5⟩\)
34) \(‖\vecs u‖=50, θ=\frac{3π}{4}\)
For exercises 35 and 36, vector \(\vecs u\) is given. Find the angle \(θ∈[0,2π)\) that vector \(\vecs u\) makes with the positive direction of the \(x\)-axis, in a counter-clockwise direction.
35) \(\vecs u=5\sqrt{2}\hat{\mathbf i}−5\sqrt{2}\hat{\mathbf j}\)
- Answer
- \(θ=\frac{7π}{4}\)
36) \(\vecs u=−\sqrt{3}\hat{\mathbf i}−\hat{\mathbf j}\)
37) Let \(\vecs a=⟨a_1,a_2⟩, \vecs b=⟨b_1,b_2⟩\), and \(\vecs c =⟨c_1,c_2⟩\) be three nonzero vectors. If \(a_1b_2−a_2b_1≠0\), then show there are two scalars, \(α\) and \(β\), such that \(\vecs c=α\vecs a+β\vecs b.\)
Answer Answers may vary
38) Consider vectors \(\vecs a=⟨2,−4⟩, \vecs b=⟨−1,2⟩,\) and \(\vecs c =\vecs 0\) Determine the scalars \(α\) and \(β\) such that \(\vecs c=α\vecs a+β\vecs b\).
39) Let \(P(x_0,f(x_0))\) be a fixed point on the graph of the differentiable function \(f\) with a domain that is the set of real numbers.
a. Determine the real number \(z_0\) such that point \(Q(x_0+1,z_0)\) is situated on the line tangent to the graph of \(f\) at point \(P\).
b. Determine the unit vector \(\vecs u\) with initial point \(P\) and terminal point \(Q\).
- Answer
- \(a. \quad z_0=f(x_0)+f′(x_0); \quad b. \quad \vecs u=\frac{1}{\sqrt{1+[f′(x_0)]^2}}⟨1,f′(x_0)⟩\)
40) Consider the function \(f(x)=x^4,\) where \(x∈R\).
a. Determine the real number \(z_0\) such that point \(Q(2,z_0)\) s situated on the line tangent to the graph of \(f\) at point \(P(1,1)\).
b. Determine the unit vector \(\vecs u\) with initial point \(P\) and terminal point \(Q\).
41) Consider \(f\) and \(g\) two functions defined on the same set of real numbers \(D\). Let \(\vecs a=⟨x,f(x)⟩\) and \(\vecs b=⟨x,g(x)⟩\) be two vectors that describe the graphs of the functions, where \(x∈D\). Show that if the graphs of the functions \(f\) and \(g\) do not intersect, then the vectors \(\vecs a\) and \(\vecs b\) are not equivalent.
42) Find \(x∈R\) such that vectors \(\vecs a=⟨x, \sin x⟩\) and \(\vecs b=⟨x, \cos x⟩\) are equivalent.
43) Calculate the coordinates of point \(D\) such that \(ABCD\) is a parallelogram, with \(A(1,1), B(2,4)\), and \(C(7,4)\).
- Answer
- \(D(6,1)\)
44) Consider the points \(A(2,1), B(10,6), C(13,4)\), and \(D(16,−2)\). Determine the component form of vector \(\vecd{AD}\).
45) The speed of an object is the magnitude of its related velocity vector. A football thrown by a quarterback has an initial speed of \(70\) mph and an angle of elevation of \(30°\). Determine the velocity vector in mph and express it in component form. (Round to two decimal places.)
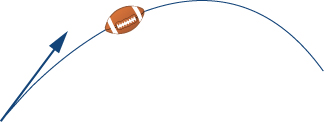
- Answer
- \(⟨60.62,35⟩\)
46) A baseball player throws a baseball at an angle of \(30°\) with the horizontal. If the initial speed of the ball is \(100\) mph, find the horizontal and vertical components of the initial velocity vector of the baseball. (Round to two decimal places.)
47) A bullet is fired with an initial velocity of \(1500\) ft/sec at an angle of \(60°\) with the horizontal. Find the horizontal and vertical components of the velocity vector of the bullet. (Round to two decimal places.)
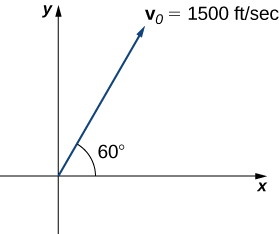
- Answer
- The horizontal and vertical components are \(750\) ft/sec and \(1299.04\) ft/sec, respectively.
48) [T] A 65-kg sprinter exerts a force of \(798\) N at a \(19°\) angle with respect to the ground on the starting block at the instant a race begins. Find the horizontal component of the force. (Round to two decimal places.)
49) [T] Two forces, a horizontal force of \(45\) lb and another of \(52\) lb, act on the same object. The angle between these forces is \(25°\). Find the magnitude and direction angle from the positive \(x\)-axis of the resultant force that acts on the object. (Round to two decimal places.)
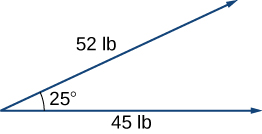
- Answer
- The magnitude of resultant force is \(94.71\) lb; the direction angle is \(13.42°\).
50) [T] Two forces, a vertical force of \(26\) lb and another of \(45\) lb, act on the same object. The angle between these forces is \(55°\). Find the magnitude and direction angle from the positive \(x\)-axis of the resultant force that acts on the object. (Round to two decimal places.)
51) [T] Three forces act on object. Two of the forces have the magnitudes \(58\) N and \(27\) N, and make angles \(53°\) and \(152°\), respectively, with the positive \(x\)-axis. Find the magnitude and the direction angle from the positive \(x\)-axis of the third force such that the resultant force acting on the object is zero. (Round to two decimal places.)
- Answer
- The magnitude of the third vector is \(60.03\) N; the direction angle is \(259.38°\).
52) Three forces with magnitudes 80 lb, 120 lb, and 60 lb act on an object at angles of \(45°, 60°\) and \(30°\), respectively, with the positive \(x\)-axis. Find the magnitude and direction angle from the positive \(x\)-axis of the resultant force. (Round to two decimal places.)
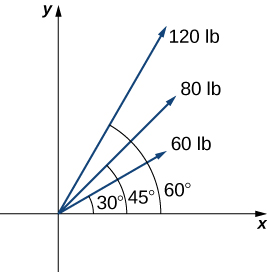
53) [T] An airplane is flying in the direction of \(43°\) east of north (also abbreviated as \(N43E\) at a speed of \(550\) mph. A wind with speed \(25\) mph comes from the southwest at a bearing of \(N15E\). What are the ground speed and new direction of the airplane?
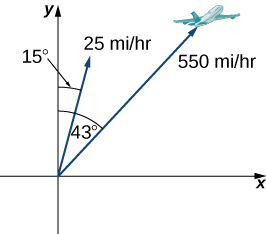
- Answer
- The new ground speed of the airplane is \(572.19\) mph; the new direction is \(N41.82E.\)
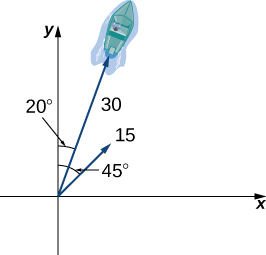
54) [T] A boat is traveling in the water at \(30\) mph in a direction of \(N20E\) (that is, \(20°\) east of north). A strong current is moving at \(15\) mph in a direction of \(N45E\). What are the new speed and direction of the boat?
55) [T] A 50-lb weight is hung by a cable so that the two portions of the cable make angles of \(40°\) and \(53°\), respectively, with the horizontal. Find the magnitudes of the forces of tension \(\vecs T_1\) and \(\vecs T_2\) in the cables if the resultant force acting on the object is zero. (Round to two decimal places.)
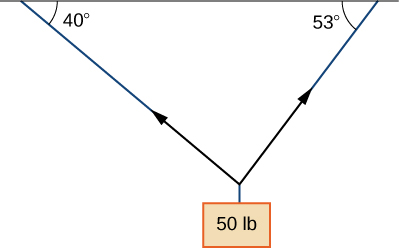
- Answer
- \(\|\vecs T_1\|=30.13 \, lb, \quad \|\vecs T_2\|=38.35 \, lb\)
56) [T] A 62-lb weight hangs from a rope that makes the angles of \(29°\) and \(61°\), respectively, with the horizontal. Find the magnitudes of the forces of tension \(\vecs T_1\) and \(\vecs T_2\) in the cables if the resultant force acting on the object is zero. (Round to two decimal places.)
57) [T] A 1500-lb boat is parked on a ramp that makes an angle of \(30°\) with the horizontal. The boat’s weight vector points downward and is a sum of two vectors: a horizontal vector \(\vecs v_1\) that is parallel to the ramp and a vertical vector \(\vecs v_2\) that is perpendicular to the inclined surface. The magnitudes of vectors \(\vecs v_1\) and \(\vecs v_2\) are the horizontal and vertical component, respectively, of the boat’s weight vector. Find the magnitudes of \(\vecs v_1\) and \(\vecs v_2\). (Round to the nearest integer.)
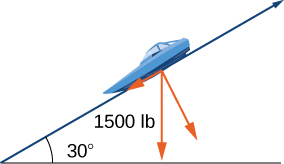
- Answer
- \(\|\vecs v_1\|=750 \, lb, \quad \|\vecs v_2\|=1299 \, lb\)
58) [T] An 85-lb box is at rest on a \(26°\) incline. Determine the magnitude of the force parallel to the incline necessary to keep the box from sliding. (Round to the nearest integer.)
59) A guy-wire supports a pole that is \(75\) ft high. One end of the wire is attached to the top of the pole and the other end is anchored to the ground \(50\) ft from the base of the pole. Determine the horizontal and vertical components of the force of tension in the wire if its magnitude is \(50\) lb. (Round to the nearest integer.)
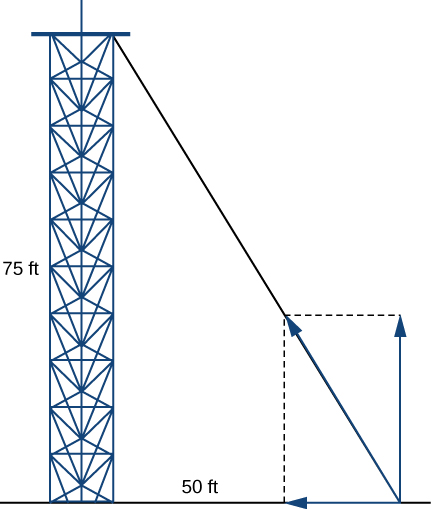
- Answer
- The two horizontal and vertical components of the force of tension are \(28\) lb and \(42\) lb, respectively.
60) A telephone pole guy-wire has an angle of elevation of \(35°\) with respect to the ground. The force of tension in the guy-wire is \(120\) lb. Find the horizontal and vertical components of the force of tension. (Round to the nearest integer.)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

