6.4: Solve Quadratic Equations in Quadratic Form
- Page ID
- 29077
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Solve equations in quadratic form
Before you get started
... take this readiness quiz.
- Factor by substitution: y4−y2−20.
- Factor by substitution: (y−4)2+8(y−4)+15.
- Simplify
- x12⋅x14
- (x13)2
- (x−1)2
Solve Equations in Quadratic Form
Sometimes when we factored trinomials, the trinomial did not appear to be in the ax2+bx+c form. So we factored by substitution allowing us to make it fit the ax2+bx+c form. We used the standard u for the substitution.
To factor the expression x4−4x2−5, we noticed the variable part of the middle term is x2 and its square, x4, is the variable part of the first term. (We know (x2)2=x4.) So we let u=x2 and factored.
| x4−4x2−5 | |
| (x2)2−4(x2)−5 | |
| Let u=x2 and substitute. | u2−4u−5 |
| Factor the trinomial. | (u+1)(u−5) |
| Replace u with x2. | (x2+1)(x2−5) |
Similarly, sometimes an equation is not in the ax2+bx+c=0 form but looks much like a quadratic equation. Then, we can often make a thoughtful substitution that will allow us to make it fit the ax2+bx+c=0 form. If we can make it fit the form, we can then use all of our methods to solve quadratic equations.
Notice that in the quadratic equation ax2+bx+c=0, the middle term has a variable, x, and its square, x2, is the variable part of the first term. Look for this relationship as you try to find a substitution.
Again, we will use the standard u to make a substitution that will put the equation in quadratic form. If the substitution gives us an equation of the form ax2+bx+c=0, we say the original equation was of quadratic form.
The next example shows the steps for solving an equation in quadratic form.
Example 6.4.1 How to Solve Equations in Quadratic Form
Solve: 6x4−7x2+2=0
Solution:
| Step 1: Identify a substitution that will put the equation in quadratic form. | Since (x2)2=x4, we let u=x2. | 6x4−7x2+2=0 |
| Step 2: Rewrite the equation with the substitution to put it in quadratic form. |
Rewrite to prepare for the substitution. Substitute u=x2. |
6(x2)2−7x2+2=06u2−7u+2=0 |
| Step 3: Solve the quadratic equation for u. |
We can solve by factoring. Use the Zero Product Property. |
(2u−1)(3u−2)=02u−1=0,3u−2=02u=1,3u=2u=12u=23 |
| Step 4: Substitute the original variable back into the results, using the substitution. | Replace u with x2. | x2=12x2=23 |
| Step 5: Solve for the original variable. | Solve for x, using the Square Root Property. |
x=±√12x=±√23x=±√22x=±√63 There are four solutions. x=√22x=√63x=−√22x=−√63 |
| Step 6: Check the solutions. | Check all four solutions. We will show one check here. |
x=√226x4−7x2+2=06(√22)4−7(√22)2+2?=06(416)−7(24)2+2?=032−72+42?=00=0 We leave the other checks to you! |
Exercise 6.4.1
Solve: x4−6x2+8=0.
- Answer
-
x=√2,x=−√2,x=2,x=−2
Exercise 6.4.2
Solve: x4−11x2+28=0.
- Answer
-
x=√7,x=−√7,x=2,x=−2
We summarize the steps to solve an equation in quadratic form.
Solve Equations in Quadratic Form
- Identify a substitution that will put the equation in quadratic form.
- Rewrite the equation with the substitution to put it in quadratic form.
- Solve the quadratic equation for u.
- Substitute the original variable back into the results, using the substitution.
- Solve for the original variable.
- Check the solutions.
In the next example, the binomial in the middle term, (x−2) is squared in the first term. If we let u=x−2 and substitute, our trinomial will be in ax2+bx+c form.
Example 6.4.2
Solve: (x−2)2+7(x−2)+12=0.
Solution:
| (x−2)2+7(x−2)+12=0 | |
| Prepare for the substitution. | (x−2)2+7(x−2)+12=0 |
| Let u=x−2 and substitute. | u2+7u+12=0 |
| Solve by factoring. |
(u+3)(u+4)=0 u+3=0,u+4=0u=−3,u=−4 |
|
Replace u with x−2. |
x−2=−3,x−2=−4 |
|
Solve for x. |
x=−1,x=−2 |
|
Check: 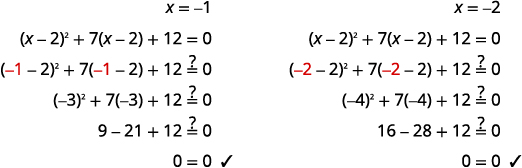
|
Exercise 6.4.3
Solve: (x−5)2+6(x−5)+8=0.
- Answer
-
x=3,x=1
Exercise 6.4.4
Solve: (y−4)2+8(y−4)+15=0.
- Answer
-
y=−1,y=1
In the next example, we notice that (√x)2=x. Also, remember that when we square both sides of an equation, we may introduce extraneous roots. Be sure to check your answers!
Example 6.4.3
Solve: x−3√x+2=0.
Solution:
The √x in the middle term, is squared in the first term (√x)2=x. If we let u=√x and substitute, our trinomial will be in ax2+bx+c=0 form.
| x−3√x+2=0 | |
| Rewrite the trinomial to prepare for the substitution. | 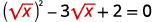 |
| Let u=√x and substitute. | 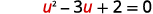 |
| Solve by factoring. |
(u−2)(u−1)=0 u−2=0,u−1=0 |
| Replace u with √x. |
√x=2,√x=1 |
| Solve for x, by squaring both sides. | x=4,x=1 |
|
Check: 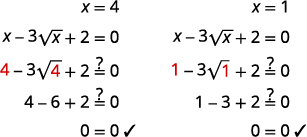 |
Exercise 6.4.5
Solve: x−7√x+12=0.
- Answer
-
x=9,x=16
Exercise 6.4.6
Solve: x−6√x+8=0.
- Answer
-
x=4,x=16
Substitutions for rational exponents can also help us solve an equation in quadratic form. Think of the properties of exponents as you begin the next example.
Example 6.4.4
Solve: x23−2x13−24=0.
Solution:
The x13 in the middle term is squared in the first term (x13)2=x23. If we let u=x13 and substitute, our trinomial will be in ax2+bx+c=0 form.
| x23−2x13−24=0 | |
| Rewrite the trinomial to prepare for the substitution. | 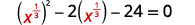 |
| Let u=x13 |  |
| Solve by factoring. |
(u−6)(u+4)=0 u−6=0,u+4=0 u=6,u=−4 |
| Replace u with x13. |
x13=6,x13=−4 |
| Solve for x by cubing both sides. |
(x13)3=(6)3,(x13)3=(−4)3 x=216,x=−64 |
|
Check: 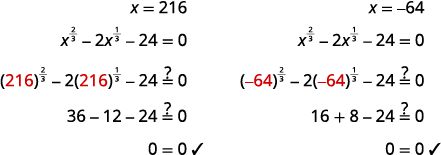
|
Exercise 6.4.7
Solve: x23−5x13−14=0.
- Answer
-
x=−8,x=343
Exercise 6.4.8
Solve: x12+8x14+15=0.
- Answer
-
x=81,x=625
In the next example, we need to keep in mind the definition of a negative exponent as well as the properties of exponents.
Example 6.4.5
Solve: 3x−2−7x−1+2=0.
Solution:
The x−1 in the middle term is squared in the first term (x−1)2=x−2. If we let u=x−1 and substitute, our trinomial will be in ax2+bx+c=0 form.
| 3x−2−7x−1+2=0 | |
| Rewrite the trinomial to prepare for the substitution. | 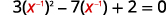 |
| Let u=x−1 and substitute. | 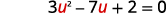 |
| Solve by factoring. | (3u−1)(u−2)=0 |
| 3u−1=0,u−2=0 | |
| u=13,u=2 | |
| Replace u with x−1. | x−1=13,x−1=2 |
| Solve for x by taking the reciprocal since x−1=1x. | x=3,x=12 |
|
Check: 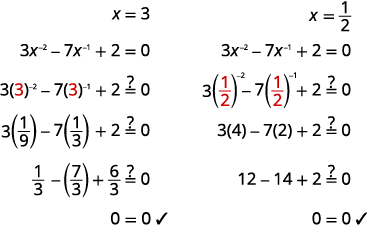
|
Exercise 6.4.9
Solve: 8x−2−10x−1+3=0.
- Answer
-
x=43,x=2
Exercise 6.4.10
Solve: 6x−2−23x−1+20=0.
- Answer
-
x=25,x=34
Access this online video for additional instruction and practice with solving quadratic equations: https://www.youtube.com/watch?v=7X-CZMbpxuw
Key Concepts
- How to solve equations in quadratic form.
- Identify a substitution that will put the equation in quadratic form.
- Rewrite the equation with the substitution to put it in quadratic form.
- Solve the quadratic equation for u.
- Substitute the original variable back into the results, using the substitution.
- Solve for the original variable.
- Check the solutions.


