4.E: Exercises

Exercise $\PageIndex{1}$

Show the map $T$: $\mathbb{R}^n → \mathbb{R}^m$ defined by $T (\vec{x}) = A\vec{x}$ where $A$ is an $m\times n$ matrix and $\vec{x}$ is an $m\times 1$ column vector is a linear transformation.

Answer

This result follows from the properties of matrix multiplication.

Exercise $\PageIndex{2}$

Show that the function $T_{\vec{u}}$ defined by $T_{\vec{u}} (\vec{v}) =\vec{v}−proj_{\vec{u}} (\vec{v})$ is also a linear transformation.

Answer

$$\begin{aligned}T_{\vec{u}}(a\vec{v}+b\vec{w})&=a\vec{v}+b\vec{w}-\frac{(a\vec{v}+b\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=a\vec{v}-a\frac{(\vec{v}\bullet\vec{u})}{||\vec{u}||^2}\vec{u}+b\vec{w}-b\frac{(\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=aT_{\vec{u}}(\vec{v})+bT_{\vec{u}}(\vec{w})\end{aligned}$$

Exercise $\PageIndex{3}$

Let $\vec{u}$ be a fixed vector. The function $T_{\vec{u}}$ defined by $T_{\vec{u}}\vec{v} =\vec{u}+\vec{v}$ has the effect of translating all vectors by adding $\vec{u}\neq\vec{0}$. Show this is not a linear transformation. Explain why it is not possible to represent $T_{\vec{u}}$ in $\mathbb{R}^3$ by multiplying by a $3×3$ matrix.

Answer

Linear transformations take $\vec{0}$ to $\vec{0}$ which $T$ does not. Also $T_{\vec{a}} (\vec{u}+\vec{v})\neq T_{\vec{a}}\vec{u}+T_{\vec{a}}\vec{v}$.

Exercise $\PageIndex{4}$

Consider the following functions which map $\mathbb{R}^n$ to $\mathbb{R}^n$.

1. $T$ multiplies the $j$th component of $\vec{x}$ by a nonzero number $b$.
2. $T$ replaces the $i$th component of $\vec{x}$ with $b$ times the $j$th component added to the $i$th component.
3. $T$ switches the $i$th and $j$th components.

Show these functions are linear transformations and describe their matrices $A$ such that $T (\vec{x}) = A\vec{x}$.

Answer

1. The matrix of $T$ is the elementary matrix which multiplies the $j$th diagonal entry of the identity matrix by $b$.
2. The matrix of $T$ is the elementary matrix which takes $b$ times the $j$th row and adds to the $i$th row.
3. The matrix of $T$ is the elementary matrix which switches the $i$th and the $j$th rows where the two components are in the $i$th and $j$th positions.

Exercise $\PageIndex{5}$

You are given a linear transformation $T$ : $\mathbb{R}^n → \mathbb{R}^m$ and you know that $$T(A_i)=B_i\nonumber$$ where $[A_1\cdots a_n]^{-1}$ exists. Show that the matrix of $T$ is of the form $$[B_1\cdots B_n][A_1\cdots A_n]^{-1}\nonumber$$

Answer

Suppose $$\left[\begin{array}{c}\vec{c}_1^{T} \\ \vdots \\ \vec{c}_n^T \end{array}\right]=\left[\begin{array}{ccc}\vec{a}_1&\cdots &\vec{a}_n\end{array}\right]^{-1}\nonumber$$ Thus $\vec{c}_i^T\vec{a}_j=\delta_{ij}$. Therefore $$\begin{aligned} \left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i&=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{c}\vec{c}_1^T \\ \vdots \\ \vec{c}_n^T\end{array}\right]\vec{a}_i\\ &=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\vec{e}_i \\ &=\vec{b}_i\end{aligned}$$ Thus $T\vec{a}_i=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i=A\vec{a}_i$. If $\vec{x}$ is arbitrary, then since the matrix $\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]$ is invertible, there exists a unique $\vec{y}$ such that $\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\vec{y}=\vec{x}$ Hence $$T\vec{x}=T\left(\sum\limits_{i=1}^n y_i\vec{a}_i\right)=\sum\limits_{i=1}^n y_iT\vec{a}_i=\sum\limits_{i=1}^n y_iA\vec{a}_i=A\left(\sum\limits_{i=1}^ny_i\vec{a}_i\right)=A\vec{x}\nonumber$$

Exercise $\PageIndex{6}$

Suppose $T$ is a linear transformation such that $$\begin{aligned}T\left[\begin{array}{r}1\\2\\-6\end{array}\right]&=\left[\begin{array}{r}5\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\5\end{array}\right]&=\left[\begin{array}{r}1\\1\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-2\end{array}\right]\end{aligned}$$ Find the matrix of $T$. That is find $A$ such that $T(\vec{x}) = A\vec{x}$.

Answer

$$\left[\begin{array}{ccc}5&1&5\\1&1&3\\3&5&-2\end{array}\right]\left[\begin{array}{ccc}3&2&1\\2&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}37&17&11 \\ 17&7&5\\11&14&6\end{array}\right]\nonumber$$

Exercise $\PageIndex{7}$

Suppose $T$ is a linear transformation such that $$\begin{aligned}T\left[\begin{array}{r}1\\1\\-8\end{array}\right]&=\left[\begin{array}{r}1\\3\\1\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}2\\4\\1\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\3\end{array}\right]&=\left[\begin{array}{r}6\\1\\-1\end{array}\right]\end{aligned}$$ Find the matrix of $T$. That is find $A$ such that $T(\vec{x})=A\vec{x}$.

Answer

$$\left[\begin{array}{ccc}1&2&6\\3&4&1\\1&1&-1\end{array}\right]\left[\begin{array}{ccc}6&3&1\\5&3&1\\6&2&1\end{array}\right]=\left[\begin{array}{ccc}52&21&9\\44&23&8\\5&4&1\end{array}\right]\nonumber$$

Exercise $\PageIndex{8}$

Suppose $T$ is a linear transformation such that $$\begin{aligned}T\left[\begin{array}{r}1\\3\\-7\end{array}\right]&=\left[\begin{array}{r}-3\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-2\\6\end{array}\right]&=\left[\begin{array}{r}1\\3\\-3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-3\end{array}\right]\end{aligned}$$ Find the matrix of $T$. That is find $A$ such that $T(\vec{x})=A\vec{x}$.

Answer

$$\left[\begin{array}{ccc}-3&1&5\\1&3&3\\3&-3&-3\end{array}\right]\left[\begin{array}{ccc}2&2&1\\1&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}15&1&3\\17&11&7\\-9&-3&-3\end{array}\right]\nonumber$$

Exercise $\PageIndex{9}$

Suppose $T$ is a linear transformation such that $$\begin{aligned}T\left[\begin{array}{r}1\\1\\-7\end{array}\right]&=\left[\begin{array}{r}3\\3\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}1\\2\\3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}1\\3\\-1\end{array}\right]\end{aligned}$$ Find the matrix of $T$. That is find $A$ such that $T(\vec{x})=A\vec{x}$.

Answer

$$\left[\begin{array}{ccc}3&1&1\\3&2&3\\3&3&-1\end{array}\right]\left[\begin{array}{ccc}6&2&1\\5&2&1\\6&1&1\end{array}\right]=\left[\begin{array}{ccc}29&9&5\\46&13&8\\27&11&5\end{array}\right]\nonumber$$

Exercise $\PageIndex{10}$

Suppose $T$ is a linear transformation such that $$\begin{aligned}T\left[\begin{array}{r}1\\2\\-18\end{array}\right]&=\left[\begin{array}{r}5\\2\\5\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\15\end{array}\right]&=\left[\begin{array}{r}3\\3\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\4\end{array}\right]&=\left[\begin{array}{r}2\\5\\-2\end{array}\right]\end{aligned}$$ Find the matrix of $T$. That is find $A$ such that $T(\vec{x})=A\vec{x}$.

Answer

$$\left[\begin{array}{ccc}5&3&2\\2&3&5\\5&5&-2\end{array}\right]\left[\begin{array}{ccc}11&4&1\\10&4&1\\12&3&1\end{array}\right]=\left[\begin{array}{ccc}109&38&10\\112&35&10\\81&34&8\end{array}\right]\nonumber$$

Exercise $\PageIndex{11}$

Consider the following functions $T : \mathbb{R}^3 → \mathbb{R}^2$. Show that each is a linear transformation and determine for each the matrix $A$ such that $T(\vec{x}) = A\vec{x}$.

1. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y-3x+z\end{array}\right]$
2. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}7x+2y+z \\ 3x-11y+2z\end{array}\right]$
3. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}3x+2y+z \\ x+2y+6z\end{array}\right]$
4. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}2y-5x+z \\ x+y+z\end{array}\right]$

Exercise $\PageIndex{12}$

Consider the following functions $T : \mathbb{R}^3 → \mathbb{R}^2$. Explain why each of these functions $T$ is not linear.

1. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z+1 \\ 2y-3x+z\end{array}\right]$
2. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y^2+3z \\ 2y+3x+z\end{array}\right]$
3. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}\sin x+2y+3z \\ 2y+3x+z\end{array}\right]$
4. $T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y+3x-\ln z\end{array}\right]$

Exercise $\PageIndex{13}$

Suppose $$[A_1\cdots A_n]^{-1}\nonumber$$ exists where each $A_j ∈ \mathbb{R}^n$ and let vectors $\{B_1,\cdots ,B_n\}$ in $\mathbb{R}^m$ be given. Show that there always exists a linear transformation $T$ such that $T(A_i) = B_i$.

Exercise $\PageIndex{14}$

Find the matrix for $T (\vec{w}) = proj_{\vec{v}}(\vec{w})$ where $\vec{v}=\left[\begin{array}{ccc}1&-2&3\end{array}\right]^T$.

Answer

Recall that $proj_{\vec{u}}(\vec{v})=\frac{\vec{v}\bullet\vec{u}}{||\vec{u}||^2}\vec{u}$ and so the desired matrix has $i$th column equal to $proj_{\vec{u}}(\vec{e}_i)$. Therefore, the matrix desired is $$\frac{1}{14}\left[\begin{array}{ccc}1&-2&3\\-2&4&-6\\3&-6&9\end{array}\right]\nonumber$$

Exercise $\PageIndex{15}$

Find the matrix for $T (\vec{w}) = proj_{\vec{v}}(\vec{w})$ where $\vec{v}=\left[\begin{array}{ccc}1&5&3\end{array}\right]^T$.

Answer

$$\frac{1}{35}\left[\begin{array}{ccc}1&5&3\\5&25&15\\3&15&9\end{array}\right]\nonumber$$

Exercise $\PageIndex{16}$

Find the matrix for $T (\vec{w}) = proj_{\vec{v}}(\vec{w})$ where $\vec{v}=\left[\begin{array}{ccc}1&0&3\end{array}\right]^T$.

Answer

$$\frac{1}{10}\left[\begin{array}{ccc}1&0&3\\0&0&0\\3&0&9\end{array}\right]\nonumber$$

Exercise $\PageIndex{17}$

Show that if a function $T :\mathbb{R}^n → \mathbb{R}^m$ is linear, then it is always the case that $T(\vec{0})=\vec{0}$.

Exercise $\PageIndex{18}$

Let $T$ be a linear transformation induced by the matrix $A=\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]$ and $S$ a linear transformation induced by $B=\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]$. Find matrix of $S\circ T$ and find $(S\circ T)(\vec{x})$ for $\vec{x}=\left[\begin{array}{r}2\\-1\end{array}\right]$.

Answer

The matrix of $S\circ T$ is given by $BA$. $$\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]=\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\nonumber$$ Now, $(S\circ T)(\vec{x})=(BA)\vec{x}$. $$\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\left[\begin{array}{c}2\\-1\end{array}\right]=\left[\begin{array}{c}8\\12\end{array}\right]\nonumber$$

Exercise $\PageIndex{19}$

Let $T$ be a linear transformation and suppose $T\left(\left[\begin{array}{r}1\\-4\end{array}\right]\right)=\left[\begin{array}{r}2\\-3\end{array}\right]$. Suppose $S$ is a linear transformation induced by the matrix $B=\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]$. Find $(S\circ T)(\vec{x})$ for $\vec{x}=\left[\begin{array}{r}1\\-4\end{array}\right]$.

Answer

To find $(S\circ T)(\vec{x})$ we compute $S(T(\vec{x}))$. $$\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\left[\begin{array}{c}2\\-3\end{array}\right]=\left[\begin{array}{c}-4\\-11\end{array}\right]\nonumber$$

Exercise $\PageIndex{20}$

Let $T$ be a linear transformation induced by the matrix $A=\left[\begin{array}{cc}2&3\\1&1\end{array}\right]$ and $S$ a lienar transformation induced by $B=\left[\begin{array}{cc}-1&3\\1&-2\end{array}\right]$. Find matrix of $S\circ T$ and find $(S\circ T)(\vec{x})$ for $\vec{x}=\left[\begin{array}{c}5\\6\end{array}\right]$.

Exercise $\PageIndex{21}$

Let $T$ be a linear transformation induced by the matrix $A=\left[\begin{array}{cc}2&1\\5&2\end{array}\right]$. Find the matrix of $T^{-1}$.

Answer

The matrix of $T^{-1}$ is $A^{-1}$. $$\left[\begin{array}{cc}2&1\\5&2\end{array}\right]^{-1}=\left[\begin{array}{cc}-2&1\\5&-2\end{array}\right]\nonumber$$

Exercise $\PageIndex{22}$

Let $T$ be a linear transformation induced by the matrix $A=\left[\begin{array}{cc}4&-3\\2&-2\end{array}\right]$. Find the matrix of $T^{-1}$.

Exercise $\PageIndex{23}$

Let $T$ be a linear transformation and suppose $T\left(\left[\begin{array}{c}1\\2\end{array}\right]\right)=\left[\begin{array}{c}9\\8\end{array}\right],\:T\left(\left[\begin{array}{r}0\\-1\end{array}\right]\right)=\left[\begin{array}{c}-4\\-3\end{array}\right]$. Find the matrix of $T^{-1}$.

Exercise $\PageIndex{24}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/3$.

Answer

$\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]$

Exercise $\PageIndex{25}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/4$.

Answer

$\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]$

Exercise $\PageIndex{26}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $-π/3$.

Answer

$\left[\begin{array}{cc}\cos\left(-\frac{\pi}{3}\right)&-\sin\left(-\frac{\pi}{3}\right) \\ \sin\left(-\frac{\pi}{3}\right)&\cos\left(-\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&\frac{1}{2}\sqrt{3} \\ -\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]$

Exercise $\PageIndex{27}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $2π/3$.

Answer

$\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]$

Exercise $\PageIndex{28}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/12$. Hint: Note that $\pi /12=\pi /3-\pi /4$.

Answer

$$\begin{aligned}&\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right] \\ =&\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}-\frac{1}{4}\sqrt{2}\sqrt{3} \\ \frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}\end{array}\right]\end{aligned}$$

Exercise $\PageIndex{29}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $2π/3$ and then reflects across the $x$ axis.

Answer

$$\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\nonumber$$

Exercise $\PageIndex{30}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/3$ and then reflects across the $x$ axis.

Answer

$$\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\nonumber$$

Exercise $\PageIndex{31}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/4$ and then reflects across the $x$ axis.

Answer

$$\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\\-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber$$

Exercise $\PageIndex{32}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $π/6$ and then reflects across the $x$ axis followed by a reflection across the $y$ axis.

Answer

$$\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber$$

Exercise $\PageIndex{33}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ across the $x$ axis and then rotates every vector through an angle of $\pi /4$.

Answer

$$\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber$$

Exercise $\PageIndex{34}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ across the $y$ axis and then rotates every vector through an angle of $\pi /4$.

Answer

$$\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber$$

Exercise $\PageIndex{35}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ across the $x$ axis and then rotates every vector through an angle of $\pi /6$.

Answer

$$\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{3}&\frac{1}{2} \\ \frac{1}{2}&-\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber$$

Exercise $\PageIndex{36}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ across the $y$ axis and then rotates every vector through an angle of $\pi /6$.

Answer

$$\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&-\frac{1}{2} \\ -\frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber$$

Exercise $\PageIndex{37}$

Find the matrix for the linear transformation which rotates every vector in $\mathbb{R}^2$ through an angle of $5\pi /12$. Hint: Note that $5\pi /12=2\pi /3-\pi /4$.

Answer

$$\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right]=\nonumber$$ $$\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&-\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2} \\ \frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}\end{array}\right]\nonumber$$ Note that it doesn't matter about the order in this case.

Exercise $\PageIndex{38}$

Find the matrix of the linear transformation which rotates every vector in $\mathbb{R}^3$ counter clockwise about the $z$ axis when viewed from the positive $z$ axis through an angle of $30^◦$ and then reflects through the $xy$ plane.

Answer

$$\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right]\left[\begin{array}{ccc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right)&0 \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)&0 \\ 0&0&1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}\sqrt{3}&-\frac{1}{2}&0\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}&0\\0&0&-1\end{array}\right]\nonumber$$

Exercise $\PageIndex{39}$

Let $\vec{u}=\left[\begin{array}{c}a\\b\end{array}\right]$ be a unit vector in $\mathbb{R}^2$. Find the matrix which reflects all vectors across this vector, as shown in the following picture.

Figure $\PageIndex{1}$

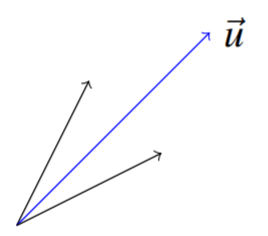
Hint: Notice that $\left[\begin{array}{c}a\\b\end{array}\right]=\left[\begin{array}{c}\cos\theta \\ \sin\theta\end{array}\right]$ for some $\theta$. First rotate through $-\theta$. Next reflect through the $x$ axis. Finally rotate through $\theta$.

Answer

$$\begin{aligned} &\left[\begin{array}{cc}\cos (\theta )&-\sin(\theta) \\ \sin(\theta)&\cos(\theta)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos(-\theta)&-\sin(\theta) \\ \sin(-\theta)&\cos(-\theta)\end{array}\right] \\ =&\left[\begin{array}{cc}\cos^2\theta-\sin^2\theta &2\cos\theta\sin\theta \\ 2\cos\theta\sin\theta&\sin^2\theta-\cos^2\theta\end{array}\right]\end{aligned}$$ Now to write in terms of $(a,b)$, note that $a/\sqrt{a^2+b^2}=\cos\theta$, $b/\sqrt{a^2+b^2}=\sin\theta$. Now plug this in to the above. The result is $$\left[\begin{array}{cc}\frac{a^2-b^2}{a^2+b^2}&2\frac{ab}{a^2+b^2} \\ 2\frac{ab}{a^2+b^2}&\frac{b^2-a^2}{a^2+b^2}\end{array}\right]=\frac{1}{a^2+b^2}\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber$$ Since this is a unit vector, $a^2+b^2=1$ and so you get $$\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber$$

Exercise $\PageIndex{40}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}2&1\\0&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber$$ Is $T$ one to one? Is $T$ onto?

Exercise $\PageIndex{41}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}-1&2\\2&1\\1&4\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber$$ Is $T$ one to one? Is $T$ onto?

Exercise $\PageIndex{42}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}2&0&1\\1&2&-1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber$$ Is $T$ one to one? Is $T$ onto?

Exercise $\PageIndex{43}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&3&-5\\2&0&2\\2&4&-6\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber$$ Is $T$ one to one? Is $T$ onto?

Exercise $\PageIndex{44}$

Give an example of a $3\times 2$ matrix with the property that the linear transformation determined by this matrix is one to one but not onto.

Answer

$$\left[\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right]\nonumber$$

Exercise $\PageIndex{45}$

Suppose $A$ is an $m\times n$ matrix in which $m ≤ n$. Suppose also that the rank of $A$ equals $m$. Show that the transformation $T$ determined by $A$ maps $\mathbb{R}^n$ onto $\mathbb{R}^m$. Hint: The vectors $\vec{e}_1,\cdots ,\vec{e}_m$ occur as columns in the reduced row-echelon form for $A$.

Answer

This says that the columns of $A$ have a subset of $m$ vectors which are linearly independent. Therefore, this set of vectors is a basis for $\mathbb{R}^m$. It follows that the span of the columns is all of $\mathbb{R}^m$. Thus $A$ is onto.

Exercise $\PageIndex{46}$

Suppose $A$ is an $m\times n$ matrix in which $m ≥ n$. Suppose also that the rank of $A$ equals $n$. Show that $A$ is one to one. Hint: If not, there exists a vector, $\vec{x}$ such that $A\vec{x} = 0$, and this implies at least one column of $A$ is a linear combination of the others. Show this would require the rank to be less than $n$.

Answer

The columns are independent. Therefore, $A$ is one to one.

Exercise $\PageIndex{47}$

Explain why an $n\times n$ matrix $A$ is both one to one and onto if and only if its rank is $n$.

Answer

The rank is $n$ is the same as saying the columns are independent which is the same as saying $A$ is one to one which is the same as saying the columns are a basis. Thus the span of the columns of $A$ is all of $\mathbb{R}^n$ and so $A$ is onto. If $A$ is onto, then the columns must be linearly independent since otherwise the span of these columns would have dimension less than $n$ and so the dimension of $\mathbb{R}^n$ would be less than $n$.

Exercise $\PageIndex{48}$

Let $V$ and $W$ be subspaces of $\mathbb{R}^n$ and $\mathbb{R}^m$ respectively and let $T : V → W$ be a linear transformation. Suppose that $\{T\vec{v}_1,\cdots ,T\vec{v}_r\}$ is linearly independent. Show that it must be the case that $\{T\vec{v}_1,\cdots ,T\vec{v}_r\}$ is also linearly independent.

Answer

If $\sum_i^r a_i\vec{v}_r=0$, then using linearity properties of $T$ we get $$0=T(0)=T\left(\sum\limits_i^ra_i\vec{v}_r\right)=\sum\limits_i^ra_iT(\vec{v}_r).\nonumber$$ Since we assume that $\{T\vec{v}_a,\cdots ,T\vec{v}_r\}$ is linearly independent, we must have all $a_i = 0$, and therefore we conclude that $\{\vec{v}_1,\cdots ,\vec{v}_r\}$ is also linearly independent.

Exercise $\PageIndex{49}$

Let $$V=span\left\{\left[\begin{array}{c}1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\0\\1\end{array}\right]\right\}\nonumber$$ Let $T\vec{x}=A\vec{x}$ where $A$ is the matrix $$\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber$$ Give a basis for $im(T)$.

Exercise $\PageIndex{50}$

Let $$V=span\left\{\left[\begin{array}{c}1\\0\\0\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\4\\4\\1\end{array}\right]\right\}\nonumber$$ Let $T\vec{x}=A\vec{x}$ where $A$ is the matrix $$\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber$$ Find a basis for $im(T)$. In this case, the original vectors do not form an independent set.

Answer

Since the third vector is a linear combinations of the first two, then the image of the third vector will also be a linear combinations of the image of the first two. However the image of the first two vectors are linearly independent (check!), and hence form a basis of the image.

Thus a basis for $im(T)$ is: $$V=span\left\{\left[\begin{array}{c}2\\0\\1\\3\end{array}\right],\:\left[\begin{array}{c}4\\2\\4\\5\end{array}\right]\right\}\nonumber$$

Exercise $\PageIndex{51}$

If $\{\vec{v}_1,\cdots ,\vec{v}_r\}$ is linearly independent and $T$ is a one to one linear transformation, show that $\{T\vec{v}_1,\cdots ,T\vec{v}_r\}$ is also linearly independent. Give an example which shows that if $T$ is only linear, it can happen that, although $\{\vec{v}_1,\cdots ,\vec{v}_r\}$ is linearly independent, $\{T\vec{v}_1,\cdots ,T\vec{v}_r\}$ is not. In fact, show that it can happen that each of the $T\vec{v}_j$ equals $0$.

Exercise $\PageIndex{52}$

Let $V$ and $W$ be subspaces of $\mathbb{R}^n$ and $\mathbb{R}^m$ respectively and let $T : V → W$ be a linear transformation. Show that if $T$ is onto $W$ and if $\{\vec{v}_1,\cdots ,\vec{v}_r\}$ is a basis for $V$, then $span\{T\vec{v}_1,\cdots ,T\vec{v}_r\} = W$.

Exercise $\PageIndex{53}$

Define $T$: $\mathbb{R}^4\to\mathbb{R}^3$ as follows. $$T\vec{x}=\left[\begin{array}{cccc}3&2&1&8\\2&2&-2&6\\1&1&-1&3\end{array}\right]\vec{x}\nonumber$$ Find a basis for $im(T)$. Also find a basis for $\text{ker}(T)$.

Exercise $\PageIndex{54}$

Define $T$: $\mathbb{R}^3\to\mathbb{R}^3$ as follows. $$T\vec{x}=\left[\begin{array}{ccc}1&2&0\\1&1&1\\0&1&1\end{array}\right]\vec{x}\nonumber$$ where on the right, it is just matrix multiplication of the vector $\vec{x}$ which is meant. Explain why $T$ is an isomorphism of $\mathbb{R}^3$ to $\mathbb{R}^3$.

Exercise $\PageIndex{55}$

Suppose $T$: $\mathbb{R}^3\to\mathbb{R}^3$ is a linear transformation given by $$T\vec{x}=A\vec{x}\nonumber$$ where $A$ is a $3\times 3$ matrix. Show that $T$ is an isomorphism if and only if $A$ is invertible.

Exercise $\PageIndex{56}$

Suppose $T$: $\mathbb{R}^n\to\mathbb{R}^m$ is a linear transformation given by $$T\vec{x}=A\vec{x}\nonumber$$ where $A$ is an $m\times n$ matrix. Show that $T$ is never an ismorphism if $m\neq n$. In particular, show that if $m>n$, $T$ cannot be onto and if $m<n$, then $T$ cannot be one to one.

Exercise $\PageIndex{57}$

Define $T$: $\mathbb{R}^2\to\mathbb{R}^3$ as follows. $$T\vec{x}=\left[\begin{array}{cc}1&0\\1&1\\0&1\end{array}\right]\vec{x}\nonumber$$ where on the right, it is just matrix multiplication of the vector $\vec{x}$ which is meant. Show that $T$ is one to one. Next let $W = im(T)$. Show that $T$ is an isomorphism of $\mathbb{R}^2$ and $im (T)$.

Exercise $\PageIndex{58}$

In the above problem, find a $2\times 3$ matrix $A$ such that the restriction of $A$ to $im(T)$ gives the same result as $T^{−1}$ on $im(T)$. Hint: You might let $A$ be such that $$A\left[\begin{array}{c}1\\1\\0\end{array}\right]=\left[\begin{array}{c}1\\0\end{array}\right],\:A\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\end{array}\right]\nonumber$$ now find another vector $\vec{v}\in\mathbb{R}^3$ such that $$\left\{\left[\begin{array}{c}1\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right],\:\vec{v}\right\}\nonumber$$ is a basis. You could pick $$\vec{v}=\left[\begin{array}{c}0\\0\\1\end{array}\right]\nonumber$$ for example. Explain why this one works or one of your choice works. Then you could define $A\vec{v}$ to equal some vector in $\mathbb{R}^2$. Explain why there will be more than one such matrix $A$ which will deliver the inverse isomorphism $T^{−1}$ on $im(T)$.

Exercise $\PageIndex{59}$

Now let $V$ equan $span\left\{\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\right\}$ and let $T$: $V\to W$ be a linear transformation where $$W=span\left\{\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\right\}\nonumber$$ and $$T\left[\begin{array}{c}1\\0\\1\end{array}\right]=\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:T\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\nonumber$$ Explain why $T$ is an isomorphism. Determine a matrix $A$ which, when multiplied on the left gives the same result as $T$ on $V$ and a matrix $B$ which delivers $T^{−1}$ on $W$. Hint: You need to have $$A\left[\begin{array}{cc}1&0\\0&1\\1&1\end{array}\right]=\left[\begin{array}{cc}1&0\\0&1\\1&1\\0&1\end{array}\right]\nonumber$$ Now enlarge $\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]$ to obtain a basis for $\mathbb{R}^3$. You could add in $\left[\begin{array}{c}0\\0\\1\end{array}\right]$ for example, and then pick another vector in $\mathbb{R}^4$ and let $A\left[\begin{array}{c}0\\0\\1\end{array}\right]$ equal this other vector. Then you would have $$A\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&1\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&0\\0&1&1\end{array}\right]\nonumber$$ This would involve picking for the new vector in $\mathbb{R}^4$ the vector $\left[\begin{array}{cccc}0&0&0&1\end{array}\right]^T$. Then you could find $A$. You can do something similar to find a matrix for $T^{−1}$ denoted as $B$.

Exercise $\PageIndex{60}$

Let $V=\mathbb{R}^3$ and let $$W=span(S),\text{ where }S=\left\{\left[\begin{array}{r}1\\-1\\1\end{array}\right],\:\left[\begin{array}{r}-2\\2\\-2\end{array}\right],\:\left[\begin{array}{r}-1\\1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\\3\end{array}\right]\right\}\nonumber$$ Find a basis of $W$ consisting of vectors in $S$.

Answer

In this case $\text{dim}(W) = 1$ and a basis for $W$ consisting of vectors in $S$ can be obtained by taking any (nonzero) vector from $S$.

Exercise $\PageIndex{61}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber$$ Find a basis for $\text{ker}(T)$ and $im(T)$.

Answer

A basis for $\text{ker}(T)$ is $\left\{\left[\begin{array}{r}1\\-1\end{array}\right]\right\}$ and a basis for $im(T)$ is $\left\{\left[\begin{array}{c}1\\1\end{array}\right]\right\}$. There are many other possibilities for the specific bases, but in this case $\text{dim}(\text{ker}(T))=1$ and $\text{dim}(im(T))=1$.

Exercise $\PageIndex{62}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&0\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber$$ Find a basis for $\text{ker}(T)$ and $im(T)$.

Answer

In this case $\text{ker}(T)=\{0\}$ and $im(T)=\mathbb{R}^2$ (pick any basis of $\mathbb{R}^2$).

Exercise $\PageIndex{63}$

Let $V=\mathbb{R}^3$ and let $$W=span\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right]\right\}\nonumber$$ Extend this basis of $W$ to a basis of $V$.

Answer

There are many possible such extensions, one is (how do we know?): $$\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right],\:\left[\begin{array}{c}0\\0\\1\end{array}\right]\right\}\nonumber$$

Exercise $\PageIndex{64}$

Let $T$ be a linear transformation given by $$T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&1&1\\1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber$$ What is $\text{dim}(\text{ker}(T))$?

Answer

We can easily see that $\text{dim}(im(T))=1$, and thus $\text{dim}(\text{ker}(T))=3-\text{dim}(im(T))=3-1=2$.

Exercise $\PageIndex{65}$

Let $B=\left\{\left[\begin{array}{r}2\\-1\end{array}\right],\:\left[\begin{array}{r}3\\2\end{array}\right]\right\}$ be a basis of $\mathbb{R}^2$ and let $\vec{x}=\left[\begin{array}{r}5\\-7\end{array}\right]$ be a vector in $\mathbb{R}^2$. Find $C_B(\vec{x})$.

Exercise $\PageIndex{66}$

Let $B=\left\{\left[\begin{array}{r}1\\-1\\2\end{array}\right],\:\left[\begin{array}{r}2\\1\\2\end{array}\right],\:\left[\begin{array}{r}-1\\0\\2\end{array}\right]\right\}$ be a basis of $\mathbb{R}^3$ and let $\vec{x}=\left[\begin{array}{r}5\\-1\\4\end{array}\right]$ be a vector in $\mathbb{R}^2$. Find $C_B(\vec{x})$.

Answer

$C_B(\vec{x})=\left[\begin{array}{r}2\\1\\-1\end{array}\right]$

Exercise $\PageIndex{67}$

Let $T$: $\mathbb{R}^2→\mathbb{R}^2$ be a linear transformation defined by $T\left(\left[\begin{array}{c}a\\b\end{array}\right)\right]=\left[\begin{array}{c}a+b\\a-b\end{array}\right]$.

Consider the two bases $$B_1=\{\vec{v}_1,\vec{v}_2\}=\left\{\left[\begin{array}{c}1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\end{array}\right]\right\}\nonumber$$ and $$B_2=\left\{\left[\begin{array}{c}1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\nonumber$$

Find the matrix $M_{B_2,B_1}$ of $T$ with respect to the bases $B_1$ and $B_2$.

Answer

$M_{B_2B_1}=\left[\begin{array}{rr}1&0\\-1&1\end{array}\right]$

Exercise $\PageIndex{68}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-3\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}_3\in\mathbb{R}$. A basis for the solution space is $\left[\begin{array}{r}-3\\-1\\1\end{array}\right]\nonumber$

Exercise $\PageIndex{69}$

Using Exercise $\PageIndex{68}$ find the general solution to the following linear system. $$\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber$$

Answer

Note that this has the same matrix as the above problem. Solution is: $\left[\begin{array}{r}-3\hat{t}_3 \\ -\hat{t}_3 \\ \hat{t}_3\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}_3\in\mathbb{R}$

Exercise $\PageIndex{70}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]$, A basis is $\left[\begin{array}{c}3\\2\\1\end{array}\right]$

Exercise $\PageIndex{71}$

Using Exercise $\PageIndex{70}$ find the general solution to the following linear system. $$\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right] +\left[\begin{array}{c}-3\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}$

Exercise $\PageIndex{72}$

Write the solution set of the following system as a linear combination of vectors. $$\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]$. A basis is $\left[\begin{array}{r}-4\\-2\\1\end{array}\right]$

Exercise $\PageIndex{73}$

Using Exercise $\PageIndex{72}$ find the general solution to the following linear system. $$\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}$

Exercise $\PageIndex{74}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}$

Exercise $\PageIndex{75}$

Using Exercise $\PageIndex{74}$ find the general solution to the following linear system. $$\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}-1\\-1\\0\end{array}\right]$

Exercise $\PageIndex{76}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}$

Exercise $\PageIndex{77}$

Using Exercise $\PageIndex{76}$ find the general solution to the following linear system. $$\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}2\\-1\\-1\\0\end{array}\right]$

Exercise $\PageIndex{78}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{cccc}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&0&0&0\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{c}-s-t \\ s\\s\\t\end{array}\right],\:s,t\in\mathbb{R}$. A basis is $$\left\{\left[\begin{array}{r}-1\\1\\1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\0\\0\\1\end{array}\right]\right\}\nonumber$$

Exercise $\PageIndex{79}$

Using Exercise $\PageIndex{78}$ find the general solution to the following linear system. $$\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\0\end{array}\right]\nonumber$$

Answer

Solution is: $$\left[\begin{array}{r}-\hat{t}\\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{c}-8\\5\\0\\5\end{array}\right]\nonumber$$

Exercise $\PageIndex{80}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $$\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber$$ for $s,t\in\mathbb{R}$. A basis is $$\left\{\left[\begin{array}{r}-1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\\0\\1\end{array}\right]\right\}\nonumber$$

Exercise $\PageIndex{81}$

Using Exercise $\PageIndex{80}$ find the general solution to the following linear system. $$\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber$$

Answer

Solution is: $$\left[\begin{array}{r}\frac{3}{2} \\ -\frac{1}{2}\\0\\0\end{array}\right]+\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber$$

Exercise $\PageIndex{82}$

Write the solution set of the following system as a linear combination of vectors $$\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]$, a basis is $\left[\begin{array}{c}1\\1\\1\\0\end{array}\right]$.

Exercise $\PageIndex{83}$

Using Exercise $\PageIndex{82}$ find the general solution to the following linear system. $$\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\1\end{array}\right]\nonumber$$

Answer

Solution is: $\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{r}-9\\5\\0\\6\end{array}\right],t\in\mathbb{R}$.

Exercise $\PageIndex{84}$

Suppose $A\vec{x}=\vec{b}$ has a solution. Explain why the solution is unique precisely when $A\vec{x}=\vec{0}$ has only the trivial solution.

Answer

If not, then there would be a infintely many solutions to $A\vec{x}=\vec{0}$ and each of these added to a solution to $A\vec{x}=\vec{b}$ would be a solution to $A\vec{x}=\vec{b}$.