5.E: Exercises
- Page ID
- 93452
Show the map \(T\): \(\mathbb{R}^n → \mathbb{R}^m\) defined by \(T (\vec{x}) = A\vec{x}\) where \(A\) is an \(m\times n\) matrix and \(\vec{x}\) is an \(m\times 1\) column vector is a linear transformation.
- Answer
-
This result follows from the properties of matrix multiplication.
Show that the function \(T_{\vec{u}}\) defined by \(T_{\vec{u}} (\vec{v}) =\vec{v}−proj_{\vec{u}} (\vec{v})\) is also a linear transformation.
- Answer
-
\[\begin{aligned}T_{\vec{u}}(a\vec{v}+b\vec{w})&=a\vec{v}+b\vec{w}-\frac{(a\vec{v}+b\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=a\vec{v}-a\frac{(\vec{v}\bullet\vec{u})}{||\vec{u}||^2}\vec{u}+b\vec{w}-b\frac{(\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=aT_{\vec{u}}(\vec{v})+bT_{\vec{u}}(\vec{w})\end{aligned}\]
Let \(\vec{u}\) be a fixed vector. The function \(T_{\vec{u}}\) defined by \(T_{\vec{u}}\vec{v} =\vec{u}+\vec{v}\) has the effect of translating all vectors by adding \(\vec{u}\neq\vec{0}\). Show this is not a linear transformation. Explain why it is not possible to represent \(T_{\vec{u}}\) in \(\mathbb{R}^3\) by multiplying by a \(3×3\) matrix.
- Answer
-
Linear transformations take \(\vec{0}\) to \(\vec{0}\) which \(T\) does not. Also \(T_{\vec{a}} (\vec{u}+\vec{v})\neq T_{\vec{a}}\vec{u}+T_{\vec{a}}\vec{v}\).
Consider the following functions which map \(\mathbb{R}^n\) to \(\mathbb{R}^n\).
- \(T\) multiplies the \(j\)th component of \(\vec{x}\) by a nonzero number \(b\).
- \(T\) replaces the \(i\)th component of \(\vec{x}\) with \(b\) times the \(j\)th component added to the \(i\)th component.
- \(T\) switches the \(i\)th and \(j\)th components.
Show these functions are linear transformations and describe their matrices \(A\) such that \(T (\vec{x}) = A\vec{x}\).
- Answer
-
- The matrix of \(T\) is the elementary matrix which multiplies the \(j\)th diagonal entry of the identity matrix by \(b\).
- The matrix of \(T\) is the elementary matrix which takes \(b\) times the \(j\)th row and adds to the \(i\)th row.
- The matrix of \(T\) is the elementary matrix which switches the \(i\)th and the \(j\)th rows where the two components are in the \(i\)th and \(j\)th positions.
You are given a linear transformation \(T\) : \(\mathbb{R}^n → \mathbb{R}^m\) and you know that \[T(A_i)=B_i\nonumber\] where \([A_1\cdots a_n]^{-1}\) exists. Show that the matrix of \(T\) is of the form \[[B_1\cdots B_n][A_1\cdots A_n]^{-1}\nonumber\]
- Answer
-
Suppose \[\left[\begin{array}{c}\vec{c}_1^{T} \\ \vdots \\ \vec{c}_n^T \end{array}\right]=\left[\begin{array}{ccc}\vec{a}_1&\cdots &\vec{a}_n\end{array}\right]^{-1}\nonumber\] Thus \(\vec{c}_i^T\vec{a}_j=\delta_{ij}\). Therefore \[\begin{aligned} \left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i&=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{c}\vec{c}_1^T \\ \vdots \\ \vec{c}_n^T\end{array}\right]\vec{a}_i\\ &=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\vec{e}_i \\ &=\vec{b}_i\end{aligned}\] Thus \(T\vec{a}_i=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i=A\vec{a}_i\). If \(\vec{x}\) is arbitrary, then since the matrix \(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\) is invertible, there exists a unique \(\vec{y}\) such that \(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\vec{y}=\vec{x}\) Hence \[T\vec{x}=T\left(\sum\limits_{i=1}^n y_i\vec{a}_i\right)=\sum\limits_{i=1}^n y_iT\vec{a}_i=\sum\limits_{i=1}^n y_iA\vec{a}_i=A\left(\sum\limits_{i=1}^ny_i\vec{a}_i\right)=A\vec{x}\nonumber\]
Suppose \(T\) is a linear transformation such that \[\begin{aligned}T\left[\begin{array}{r}1\\2\\-6\end{array}\right]&=\left[\begin{array}{r}5\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\5\end{array}\right]&=\left[\begin{array}{r}1\\1\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-2\end{array}\right]\end{aligned}\] Find the matrix of \(T\). That is find \(A\) such that \(T(\vec{x}) = A\vec{x}\).
- Answer
-
\[\left[\begin{array}{ccc}5&1&5\\1&1&3\\3&5&-2\end{array}\right]\left[\begin{array}{ccc}3&2&1\\2&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}37&17&11 \\ 17&7&5\\11&14&6\end{array}\right]\nonumber\]
Suppose \(T\) is a linear transformation such that \[\begin{aligned}T\left[\begin{array}{r}1\\1\\-8\end{array}\right]&=\left[\begin{array}{r}1\\3\\1\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}2\\4\\1\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\3\end{array}\right]&=\left[\begin{array}{r}6\\1\\-1\end{array}\right]\end{aligned}\] Find the matrix of \(T\). That is find \(A\) such that \(T(\vec{x})=A\vec{x}\).
- Answer
-
\[\left[\begin{array}{ccc}1&2&6\\3&4&1\\1&1&-1\end{array}\right]\left[\begin{array}{ccc}6&3&1\\5&3&1\\6&2&1\end{array}\right]=\left[\begin{array}{ccc}52&21&9\\44&23&8\\5&4&1\end{array}\right]\nonumber\]
Suppose \(T\) is a linear transformation such that \[\begin{aligned}T\left[\begin{array}{r}1\\3\\-7\end{array}\right]&=\left[\begin{array}{r}-3\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-2\\6\end{array}\right]&=\left[\begin{array}{r}1\\3\\-3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-3\end{array}\right]\end{aligned}\] Find the matrix of \(T\). That is find \(A\) such that \(T(\vec{x})=A\vec{x}\).
- Answer
-
\[\left[\begin{array}{ccc}-3&1&5\\1&3&3\\3&-3&-3\end{array}\right]\left[\begin{array}{ccc}2&2&1\\1&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}15&1&3\\17&11&7\\-9&-3&-3\end{array}\right]\nonumber\]
Suppose \(T\) is a linear transformation such that \[\begin{aligned}T\left[\begin{array}{r}1\\1\\-7\end{array}\right]&=\left[\begin{array}{r}3\\3\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}1\\2\\3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}1\\3\\-1\end{array}\right]\end{aligned}\] Find the matrix of \(T\). That is find \(A\) such that \(T(\vec{x})=A\vec{x}\).
- Answer
-
\[\left[\begin{array}{ccc}3&1&1\\3&2&3\\3&3&-1\end{array}\right]\left[\begin{array}{ccc}6&2&1\\5&2&1\\6&1&1\end{array}\right]=\left[\begin{array}{ccc}29&9&5\\46&13&8\\27&11&5\end{array}\right]\nonumber\]
Suppose \(T\) is a linear transformation such that \[\begin{aligned}T\left[\begin{array}{r}1\\2\\-18\end{array}\right]&=\left[\begin{array}{r}5\\2\\5\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\15\end{array}\right]&=\left[\begin{array}{r}3\\3\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\4\end{array}\right]&=\left[\begin{array}{r}2\\5\\-2\end{array}\right]\end{aligned}\] Find the matrix of \(T\). That is find \(A\) such that \(T(\vec{x})=A\vec{x}\).
- Answer
-
\[\left[\begin{array}{ccc}5&3&2\\2&3&5\\5&5&-2\end{array}\right]\left[\begin{array}{ccc}11&4&1\\10&4&1\\12&3&1\end{array}\right]=\left[\begin{array}{ccc}109&38&10\\112&35&10\\81&34&8\end{array}\right]\nonumber\]
Consider the following functions \(T : \mathbb{R}^3 → \mathbb{R}^2\). Show that each is a linear transformation and determine for each the matrix \(A\) such that \(T(\vec{x}) = A\vec{x}\).
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y-3x+z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}7x+2y+z \\ 3x-11y+2z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}3x+2y+z \\ x+2y+6z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}2y-5x+z \\ x+y+z\end{array}\right]\)
Consider the following functions \(T : \mathbb{R}^3 → \mathbb{R}^2\). Explain why each of these functions \(T\) is not linear.
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z+1 \\ 2y-3x+z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y^2+3z \\ 2y+3x+z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}\sin x+2y+3z \\ 2y+3x+z\end{array}\right]\)
- \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y+3x-\ln z\end{array}\right]\)
Suppose \[ [A_1\cdots A_n]^{-1}\nonumber\] exists where each \(A_j ∈ \mathbb{R}^n\) and let vectors \(\{B_1,\cdots ,B_n\}\) in \(\mathbb{R}^m\) be given. Show that there always exists a linear transformation \(T\) such that \(T(A_i) = B_i\).
Find the matrix for \(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) where \(\vec{v}=\left[\begin{array}{ccc}1&-2&3\end{array}\right]^T\).
- Answer
-
Recall that \(proj_{\vec{u}}(\vec{v})=\frac{\vec{v}\bullet\vec{u}}{||\vec{u}||^2}\vec{u}\) and so the desired matrix has \(i\)th column equal to \(proj_{\vec{u}}(\vec{e}_i)\). Therefore, the matrix desired is \[\frac{1}{14}\left[\begin{array}{ccc}1&-2&3\\-2&4&-6\\3&-6&9\end{array}\right]\nonumber\]
Find the matrix for \(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) where \(\vec{v}=\left[\begin{array}{ccc}1&5&3\end{array}\right]^T\).
- Answer
-
\[\frac{1}{35}\left[\begin{array}{ccc}1&5&3\\5&25&15\\3&15&9\end{array}\right]\nonumber\]
Find the matrix for \(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) where \(\vec{v}=\left[\begin{array}{ccc}1&0&3\end{array}\right]^T\).
- Answer
-
\[\frac{1}{10}\left[\begin{array}{ccc}1&0&3\\0&0&0\\3&0&9\end{array}\right]\nonumber\]
Show that if a function \(T :\mathbb{R}^n → \mathbb{R}^m\) is linear, then it is always the case that \(T(\vec{0})=\vec{0}\).
Let \(T\) be a linear transformation induced by the matrix \(A=\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]\) and \(S\) a linear transformation induced by \(B=\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\). Find matrix of \(S\circ T\) and find \((S\circ T)(\vec{x})\) for \(\vec{x}=\left[\begin{array}{r}2\\-1\end{array}\right]\).
- Answer
-
The matrix of \(S\circ T\) is given by \(BA\). \[\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]=\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\nonumber\] Now, \((S\circ T)(\vec{x})=(BA)\vec{x}\). \[\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\left[\begin{array}{c}2\\-1\end{array}\right]=\left[\begin{array}{c}8\\12\end{array}\right]\nonumber\]
Let \(T\) be a linear transformation and suppose \(T\left(\left[\begin{array}{r}1\\-4\end{array}\right]\right)=\left[\begin{array}{r}2\\-3\end{array}\right]\). Suppose \(S\) is a linear transformation induced by the matrix \(B=\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\). Find \((S\circ T)(\vec{x})\) for \(\vec{x}=\left[\begin{array}{r}1\\-4\end{array}\right]\).
- Answer
-
To find \((S\circ T)(\vec{x})\) we compute \(S(T(\vec{x}))\). \[\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\left[\begin{array}{c}2\\-3\end{array}\right]=\left[\begin{array}{c}-4\\-11\end{array}\right]\nonumber\]
Let \(T\) be a linear transformation induced by the matrix \(A=\left[\begin{array}{cc}2&3\\1&1\end{array}\right]\) and \(S\) a lienar transformation induced by \(B=\left[\begin{array}{cc}-1&3\\1&-2\end{array}\right]\). Find matrix of \(S\circ T\) and find \((S\circ T)(\vec{x})\) for \(\vec{x}=\left[\begin{array}{c}5\\6\end{array}\right]\).
Let \(T\) be a linear transformation induced by the matrix \(A=\left[\begin{array}{cc}2&1\\5&2\end{array}\right]\). Find the matrix of \(T^{-1}\).
- Answer
-
The matrix of \(T^{-1}\) is \(A^{-1}\). \[\left[\begin{array}{cc}2&1\\5&2\end{array}\right]^{-1}=\left[\begin{array}{cc}-2&1\\5&-2\end{array}\right]\nonumber\]
Let \(T\) be a linear transformation induced by the matrix \(A=\left[\begin{array}{cc}4&-3\\2&-2\end{array}\right]\). Find the matrix of \(T^{-1}\).
Let \(T\) be a linear transformation and suppose \(T\left(\left[\begin{array}{c}1\\2\end{array}\right]\right)=\left[\begin{array}{c}9\\8\end{array}\right],\:T\left(\left[\begin{array}{r}0\\-1\end{array}\right]\right)=\left[\begin{array}{c}-4\\-3\end{array}\right]\). Find the matrix of \(T^{-1}\).
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/3\).
- Answer
-
\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/4\).
- Answer
-
\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\)
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(-π/3\).
- Answer
-
\(\left[\begin{array}{cc}\cos\left(-\frac{\pi}{3}\right)&-\sin\left(-\frac{\pi}{3}\right) \\ \sin\left(-\frac{\pi}{3}\right)&\cos\left(-\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&\frac{1}{2}\sqrt{3} \\ -\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(2π/3\).
- Answer
-
\(\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\)
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/12\). Hint: Note that \(\pi /12=\pi /3-\pi /4\).
- Answer
-
\[\begin{aligned}&\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right] \\ =&\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}-\frac{1}{4}\sqrt{2}\sqrt{3} \\ \frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}\end{array}\right]\end{aligned}\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(2π/3\) and then reflects across the \(x\) axis.
- Answer
-
\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/3\) and then reflects across the \(x\) axis.
- Answer
-
\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/4\) and then reflects across the \(x\) axis.
- Answer
-
\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\\-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(π/6\) and then reflects across the \(x\) axis followed by a reflection across the \(y\) axis.
- Answer
-
\[\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) across the \(x\) axis and then rotates every vector through an angle of \(\pi /4\).
- Answer
-
\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) across the \(y\) axis and then rotates every vector through an angle of \(\pi /4\).
- Answer
-
\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) across the \(x\) axis and then rotates every vector through an angle of \(\pi /6\).
- Answer
-
\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{3}&\frac{1}{2} \\ \frac{1}{2}&-\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) across the \(y\) axis and then rotates every vector through an angle of \(\pi /6\).
- Answer
-
\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&-\frac{1}{2} \\ -\frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]
Find the matrix for the linear transformation which rotates every vector in \(\mathbb{R}^2\) through an angle of \(5\pi /12\). Hint: Note that \(5\pi /12=2\pi /3-\pi /4\).
- Answer
-
\[\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right]=\nonumber\] \[\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&-\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2} \\ \frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}\end{array}\right]\nonumber\] Note that it doesn't matter about the order in this case.
Find the matrix of the linear transformation which rotates every vector in \(\mathbb{R}^3\) counter clockwise about the \(z\) axis when viewed from the positive \(z\) axis through an angle of \(30^◦\) and then reflects through the \(xy\) plane.
- Answer
-
\[\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right]\left[\begin{array}{ccc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right)&0 \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)&0 \\ 0&0&1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}\sqrt{3}&-\frac{1}{2}&0\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}&0\\0&0&-1\end{array}\right]\nonumber\]
Let \(\vec{u}=\left[\begin{array}{c}a\\b\end{array}\right]\) be a unit vector in \(\mathbb{R}^2\). Find the matrix which reflects all vectors across this vector, as shown in the following picture.
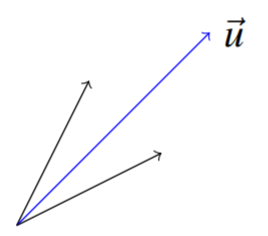
Hint: Notice that \(\left[\begin{array}{c}a\\b\end{array}\right]=\left[\begin{array}{c}\cos\theta \\ \sin\theta\end{array}\right]\) for some \(\theta\). First rotate through \(-\theta\). Next reflect through the \(x\) axis. Finally rotate through \(\theta\).
- Answer
-
\[\begin{aligned} &\left[\begin{array}{cc}\cos (\theta )&-\sin(\theta) \\ \sin(\theta)&\cos(\theta)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos(-\theta)&-\sin(\theta) \\ \sin(-\theta)&\cos(-\theta)\end{array}\right] \\ =&\left[\begin{array}{cc}\cos^2\theta-\sin^2\theta &2\cos\theta\sin\theta \\ 2\cos\theta\sin\theta&\sin^2\theta-\cos^2\theta\end{array}\right]\end{aligned}\] Now to write in terms of \((a,b)\), note that \(a/\sqrt{a^2+b^2}=\cos\theta\), \(b/\sqrt{a^2+b^2}=\sin\theta\). Now plug this in to the above. The result is \[\left[\begin{array}{cc}\frac{a^2-b^2}{a^2+b^2}&2\frac{ab}{a^2+b^2} \\ 2\frac{ab}{a^2+b^2}&\frac{b^2-a^2}{a^2+b^2}\end{array}\right]=\frac{1}{a^2+b^2}\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\] Since this is a unit vector, \(a^2+b^2=1\) and so you get \[\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\]
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}2&1\\0&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Is \(T\) one to one? Is \(T\) onto?
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}-1&2\\2&1\\1&4\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Is \(T\) one to one? Is \(T\) onto?
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}2&0&1\\1&2&-1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] Is \(T\) one to one? Is \(T\) onto?
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&3&-5\\2&0&2\\2&4&-6\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] Is \(T\) one to one? Is \(T\) onto?
Give an example of a \(3\times 2\) matrix with the property that the linear transformation determined by this matrix is one to one but not onto.
- Answer
-
\[\left[\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right]\nonumber\]
Suppose \(A\) is an \(m\times n\) matrix in which \(m ≤ n\). Suppose also that the rank of \(A\) equals \(m\). Show that the transformation \(T\) determined by \(A\) maps \(\mathbb{R}^n\) onto \(\mathbb{R}^m\). Hint: The vectors \(\vec{e}_1,\cdots ,\vec{e}_m\) occur as columns in the reduced row-echelon form for \(A\).
- Answer
-
This says that the columns of \(A\) have a subset of \(m\) vectors which are linearly independent. Therefore, this set of vectors is a basis for \(\mathbb{R}^m\). It follows that the span of the columns is all of \(\mathbb{R}^m\). Thus \(A\) is onto.
Suppose \(A\) is an \(m\times n\) matrix in which \(m ≥ n\). Suppose also that the rank of \(A\) equals \(n\). Show that \(A\) is one to one. Hint: If not, there exists a vector, \(\vec{x}\) such that \(A\vec{x} = 0\), and this implies at least one column of \(A\) is a linear combination of the others. Show this would require the rank to be less than \(n\).
- Answer
-
The columns are independent. Therefore, \(A\) is one to one.
Explain why an \(n\times n\) matrix \(A\) is both one to one and onto if and only if its rank is \(n\).
- Answer
-
The rank is \(n\) is the same as saying the columns are independent which is the same as saying \(A\) is one to one which is the same as saying the columns are a basis. Thus the span of the columns of \(A\) is all of \(\mathbb{R}^n\) and so \(A\) is onto. If \(A\) is onto, then the columns must be linearly independent since otherwise the span of these columns would have dimension less than \(n\) and so the dimension of \(\mathbb{R}^n\) would be less than \(n\).
Let \(V\) and \(W\) be subspaces of \(\mathbb{R}^n\) and \(\mathbb{R}^m\) respectively and let \(T : V → W\) be a linear transformation. Suppose that \(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) is linearly independent. Show that it must be the case that \(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) is also linearly independent.
- Answer
-
If \(\sum_i^r a_i\vec{v}_r=0\), then using linearity properties of \(T\) we get \[0=T(0)=T\left(\sum\limits_i^ra_i\vec{v}_r\right)=\sum\limits_i^ra_iT(\vec{v}_r).\nonumber\] Since we assume that \(\{T\vec{v}_a,\cdots ,T\vec{v}_r\}\) is linearly independent, we must have all \(a_i = 0\), and therefore we conclude that \(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) is also linearly independent.
Let \[V=span\left\{\left[\begin{array}{c}1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\0\\1\end{array}\right]\right\}\nonumber\] Let \(T\vec{x}=A\vec{x}\) where \(A\) is the matrix \[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Give a basis for \(im(T)\).
Let \[V=span\left\{\left[\begin{array}{c}1\\0\\0\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\4\\4\\1\end{array}\right]\right\}\nonumber\] Let \(T\vec{x}=A\vec{x}\) where \(A\) is the matrix \[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Find a basis for \(im(T)\). In this case, the original vectors do not form an independent set.
- Answer
-
Since the third vector is a linear combinations of the first two, then the image of the third vector will also be a linear combinations of the image of the first two. However the image of the first two vectors are linearly independent (check!), and hence form a basis of the image.
Thus a basis for \(im(T)\) is: \[V=span\left\{\left[\begin{array}{c}2\\0\\1\\3\end{array}\right],\:\left[\begin{array}{c}4\\2\\4\\5\end{array}\right]\right\}\nonumber\]
If \(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) is linearly independent and \(T\) is a one to one linear transformation, show that \(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) is also linearly independent. Give an example which shows that if \(T\) is only linear, it can happen that, although \(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) is linearly independent, \(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) is not. In fact, show that it can happen that each of the \(T\vec{v}_j\) equals \(0\).
Let \(V\) and \(W\) be subspaces of \(\mathbb{R}^n\) and \(\mathbb{R}^m\) respectively and let \(T : V → W\) be a linear transformation. Show that if \(T\) is onto \(W\) and if \(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) is a basis for \(V\), then \(span\{T\vec{v}_1,\cdots ,T\vec{v}_r\} = W\).
Define \(T\): \(\mathbb{R}^4\to\mathbb{R}^3\) as follows. \[T\vec{x}=\left[\begin{array}{cccc}3&2&1&8\\2&2&-2&6\\1&1&-1&3\end{array}\right]\vec{x}\nonumber\] Find a basis for \(im(T)\). Also find a basis for \(\text{ker}(T)\).
Define \(T\): \(\mathbb{R}^3\to\mathbb{R}^3\) as follows. \[T\vec{x}=\left[\begin{array}{ccc}1&2&0\\1&1&1\\0&1&1\end{array}\right]\vec{x}\nonumber\] where on the right, it is just matrix multiplication of the vector \(\vec{x}\) which is meant. Explain why \(T\) is an isomorphism of \(\mathbb{R}^3\) to \(\mathbb{R}^3\).
Suppose \(T\): \(\mathbb{R}^3\to\mathbb{R}^3\) is a linear transformation given by \[T\vec{x}=A\vec{x}\nonumber\] where \(A\) is a \(3\times 3\) matrix. Show that \(T\) is an isomorphism if and only if \(A\) is invertible.
Suppose \(T\): \(\mathbb{R}^n\to\mathbb{R}^m\) is a linear transformation given by \[T\vec{x}=A\vec{x}\nonumber\] where \(A\) is an \(m\times n\) matrix. Show that \(T\) is never an ismorphism if \(m\neq n\). In particular, show that if \(m>n\), \(T\) cannot be onto and if \(m<n\), then \(T\) cannot be one to one.
Define \(T\): \(\mathbb{R}^2\to\mathbb{R}^3\) as follows. \[T\vec{x}=\left[\begin{array}{cc}1&0\\1&1\\0&1\end{array}\right]\vec{x}\nonumber\] where on the right, it is just matrix multiplication of the vector \(\vec{x}\) which is meant. Show that \(T\) is one to one. Next let \(W = im(T)\). Show that \(T\) is an isomorphism of \(\mathbb{R}^2\) and \(im (T)\).
In the above problem, find a \(2\times 3\) matrix \(A\) such that the restriction of \(A\) to \(im(T)\) gives the same result as \(T^{−1}\) on \(im(T)\). Hint: You might let \(A\) be such that \[A\left[\begin{array}{c}1\\1\\0\end{array}\right]=\left[\begin{array}{c}1\\0\end{array}\right],\:A\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\end{array}\right]\nonumber\] now find another vector \(\vec{v}\in\mathbb{R}^3\) such that \[\left\{\left[\begin{array}{c}1\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right],\:\vec{v}\right\}\nonumber\] is a basis. You could pick \[\vec{v}=\left[\begin{array}{c}0\\0\\1\end{array}\right]\nonumber\] for example. Explain why this one works or one of your choice works. Then you could define \(A\vec{v}\) to equal some vector in \(\mathbb{R}^2\). Explain why there will be more than one such matrix \(A\) which will deliver the inverse isomorphism \(T^{−1}\) on \(im(T)\).
Now let \(V\) equan \(span\left\{\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\right\}\) and let \(T\): \(V\to W\) be a linear transformation where \[W=span\left\{\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\right\}\nonumber\] and \[T\left[\begin{array}{c}1\\0\\1\end{array}\right]=\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:T\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\nonumber\] Explain why \(T\) is an isomorphism. Determine a matrix \(A\) which, when multiplied on the left gives the same result as \(T\) on \(V\) and a matrix \(B\) which delivers \(T^{−1}\) on \(W\). Hint: You need to have \[A\left[\begin{array}{cc}1&0\\0&1\\1&1\end{array}\right]=\left[\begin{array}{cc}1&0\\0&1\\1&1\\0&1\end{array}\right]\nonumber\] Now enlarge \(\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\) to obtain a basis for \(\mathbb{R}^3\). You could add in \(\left[\begin{array}{c}0\\0\\1\end{array}\right]\) for example, and then pick another vector in \(\mathbb{R}^4\) and let \(A\left[\begin{array}{c}0\\0\\1\end{array}\right]\) equal this other vector. Then you would have \[A\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&1\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&0\\0&1&1\end{array}\right]\nonumber\] This would involve picking for the new vector in \(\mathbb{R}^4\) the vector \(\left[\begin{array}{cccc}0&0&0&1\end{array}\right]^T\). Then you could find \(A\). You can do something similar to find a matrix for \(T^{−1}\) denoted as \(B\).
Let \(V=\mathbb{R}^3\) and let \[W=span(S),\text{ where }S=\left\{\left[\begin{array}{r}1\\-1\\1\end{array}\right],\:\left[\begin{array}{r}-2\\2\\-2\end{array}\right],\:\left[\begin{array}{r}-1\\1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\\3\end{array}\right]\right\}\nonumber\] Find a basis of \(W\) consisting of vectors in \(S\).
- Answer
-
In this case \(\text{dim}(W) = 1\) and a basis for \(W\) consisting of vectors in \(S\) can be obtained by taking any (nonzero) vector from \(S\).
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Find a basis for \(\text{ker}(T)\) and \(im(T)\).
- Answer
-
A basis for \(\text{ker}(T)\) is \(\left\{\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\) and a basis for \(im(T)\) is \(\left\{\left[\begin{array}{c}1\\1\end{array}\right]\right\}\). There are many other possibilities for the specific bases, but in this case \(\text{dim}(\text{ker}(T))=1\) and \(\text{dim}(im(T))=1\).
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&0\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Find a basis for \(\text{ker}(T)\) and \(im(T)\).
- Answer
-
In this case \(\text{ker}(T)=\{0\}\) and \(im(T)=\mathbb{R}^2\) (pick any basis of \(\mathbb{R}^2\)).
Let \(V=\mathbb{R}^3\) and let \[W=span\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right]\right\}\nonumber\] Extend this basis of \(W\) to a basis of \(V\).
- Answer
-
There are many possible such extensions, one is (how do we know?): \[\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right],\:\left[\begin{array}{c}0\\0\\1\end{array}\right]\right\}\nonumber\]
Let \(T\) be a linear transformation given by \[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&1&1\\1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] What is \(\text{dim}(\text{ker}(T))\)?
- Answer
-
We can easily see that \(\text{dim}(im(T))=1\), and thus \(\text{dim}(\text{ker}(T))=3-\text{dim}(im(T))=3-1=2\).
Let \(B=\left\{\left[\begin{array}{r}2\\-1\end{array}\right],\:\left[\begin{array}{r}3\\2\end{array}\right]\right\}\) be a basis of \(\mathbb{R}^2\) and let \(\vec{x}=\left[\begin{array}{r}5\\-7\end{array}\right]\) be a vector in \(\mathbb{R}^2\). Find \(C_B(\vec{x})\).
Let \(B=\left\{\left[\begin{array}{r}1\\-1\\2\end{array}\right],\:\left[\begin{array}{r}2\\1\\2\end{array}\right],\:\left[\begin{array}{r}-1\\0\\2\end{array}\right]\right\}\) be a basis of \(\mathbb{R}^3\) and let \(\vec{x}=\left[\begin{array}{r}5\\-1\\4\end{array}\right]\) be a vector in \(\mathbb{R}^2\). Find \(C_B(\vec{x})\).
- Answer
-
\(C_B(\vec{x})=\left[\begin{array}{r}2\\1\\-1\end{array}\right]\)
Let \(T\): \(\mathbb{R}^2→\mathbb{R}^2\) be a linear transformation defined by \(T\left(\left[\begin{array}{c}a\\b\end{array}\right)\right]=\left[\begin{array}{c}a+b\\a-b\end{array}\right]\).
Consider the two bases \[B_1=\{\vec{v}_1,\vec{v}_2\}=\left\{\left[\begin{array}{c}1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\end{array}\right]\right\}\nonumber\] and \[B_2=\left\{\left[\begin{array}{c}1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\nonumber\]
Find the matrix \(M_{B_2,B_1}\) of \(T\) with respect to the bases \(B_1\) and \(B_2\).
- Answer
-
\(M_{B_2B_1}=\left[\begin{array}{rr}1&0\\-1&1\end{array}\right]\)
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-3\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}_3\in\mathbb{R}\). A basis for the solution space is \(\left[\begin{array}{r}-3\\-1\\1\end{array}\right]\nonumber\)
Using Exercise \(\PageIndex{68}\) find the general solution to the following linear system. \[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]
- Answer
-
Note that this has the same matrix as the above problem. Solution is: \(\left[\begin{array}{r}-3\hat{t}_3 \\ -\hat{t}_3 \\ \hat{t}_3\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}_3\in\mathbb{R}\)
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]\), A basis is \(\left[\begin{array}{c}3\\2\\1\end{array}\right]\)
Using Exercise \(\PageIndex{70}\) find the general solution to the following linear system. \[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right] +\left[\begin{array}{c}-3\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)
Write the solution set of the following system as a linear combination of vectors. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]\). A basis is \(\left[\begin{array}{r}-4\\-2\\1\end{array}\right]\)
Using Exercise \(\PageIndex{72}\) find the general solution to the following linear system. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)
Using Exercise \(\PageIndex{74}\) find the general solution to the following linear system. \[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}-1\\-1\\0\end{array}\right]\)
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)
Using Exercise \(\PageIndex{76}\) find the general solution to the following linear system. \[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}2\\-1\\-1\\0\end{array}\right]\)
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{cccc}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&0&0&0\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{c}-s-t \\ s\\s\\t\end{array}\right],\:s,t\in\mathbb{R}\). A basis is \[\left\{\left[\begin{array}{r}-1\\1\\1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\0\\0\\1\end{array}\right]\right\}\nonumber\]
Using Exercise \(\PageIndex{78}\) find the general solution to the following linear system. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \[\left[\begin{array}{r}-\hat{t}\\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{c}-8\\5\\0\\5\end{array}\right]\nonumber\]
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \[\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\] for \(s,t\in\mathbb{R}\). A basis is \[\left\{\left[\begin{array}{r}-1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\\0\\1\end{array}\right]\right\}\nonumber\]
Using Exercise \(\PageIndex{80}\) find the general solution to the following linear system. \[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]
- Answer
-
Solution is: \[\left[\begin{array}{r}\frac{3}{2} \\ -\frac{1}{2}\\0\\0\end{array}\right]+\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\]
Write the solution set of the following system as a linear combination of vectors \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]\), a basis is \(\left[\begin{array}{c}1\\1\\1\\0\end{array}\right]\).
Using Exercise \(\PageIndex{82}\) find the general solution to the following linear system. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\1\end{array}\right]\nonumber\]
- Answer
-
Solution is: \(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{r}-9\\5\\0\\6\end{array}\right],t\in\mathbb{R}\).
Suppose \(A\vec{x}=\vec{b}\) has a solution. Explain why the solution is unique precisely when \(A\vec{x}=\vec{0}\) has only the trivial solution.
- Answer
-
If not, then there would be a infintely many solutions to \(A\vec{x}=\vec{0}\) and each of these added to a solution to \(A\vec{x}=\vec{b}\) would be a solution to \(A\vec{x}=\vec{b}\).