2.5E: Exercises for Section 2.5

Last updated
Save as PDF

Page ID: 102701

Zoya Kravets
Mission College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 4, write the appropriate $ ε − δ$ definition for each of the given statements.

1) $\displaystyle \lim_{x →a}f(x)=N$

2) $\displaystyle \lim_{t →b}g(t)=M$

Answer: For every $ ε >0$, there exists a $ δ >0$, so that if $0 <|t −b| < δ$, then $|g(t) −M| < ε$

3) $\displaystyle \lim_{x →c}h(x)=L$

4) $\displaystyle \lim_{x →a} φ(x)=A$

Answer: For every $ ε >0$, there exists a $ δ >0$, so that if $0 <|x −a| < δ$, then $| φ(x) −A| < ε$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →2}f(x)=2$. In the following exercises, determine a value of $ δ >0$ that satisfies each statement.

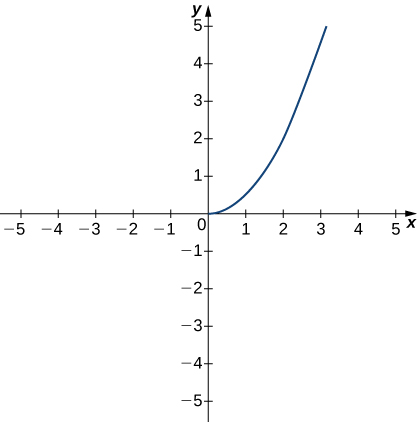
$A function drawn in quadrant one for x > 0. It is an increasing concave up function, with points approximately (0,0), (1, .5), (2,2), and (3,4).$

5) If $0 <|x −2| < δ$, then $|f(x) −2| <1$.

6) If $0 <|x −2| < δ$, then $|f(x) −2| <0.5$.

Answer: $ δ ≤0.25$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →3}f(x)= −1$. In the following exercises, determine a value of $ δ >0$ that satisfies each statement.

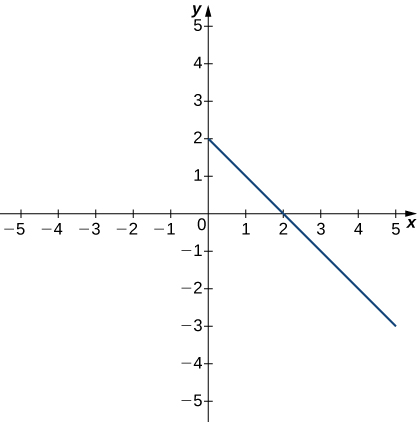
$A graph of a decreasing linear function, with points (0,2), (1,1), (2,0), (3,-1), (4,-2), and so on for x >= 0.$

7) If $0 <|x −3| < δ$, then $|f(x)+1| <1$.

8) If $0 <|x −3| < δ$, then $|f(x)+1| <2$.

Answer: $ δ ≤2$

The following graph of the function $f$ satisfies $\displaystyle \lim_{x →3}f(x)=2$. In the following exercises, for each value of $ ε$, find a value of $ δ >0$ such that the precise definition of limit holds true.

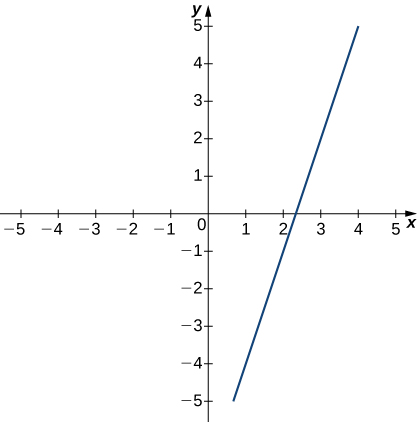
$A graph of an increasing linear function intersecting the x axis at about (2.25, 0) and going through the points (3,2) and, approximately, (1,-5) and (4,5).$

9) $ ε=1.5$

10) $ ε=3$

Answer: $ δ ≤1$

[T] In exercises 11 - 12, use a graphing calculator to find a number $ δ$ such that the statements hold true.

11) $\left|\sin(2x) −\frac{1}{2}\right| <0.1$, whenever $\left|x −\frac{ π}{12}\right| < δ$

12) $\left|\sqrt{x −4} −2\right| <0.1$, whenever $|x −8| < δ$

Answer: $ δ <0.3900$

In exercises 13 - 17, use the precise definition of limit to prove the given limits.

13) $\displaystyle \lim_{x →2}\,(5x+8)=18$

14) $\displaystyle \lim_{x →3}\frac{x^2 −9}{x −3}=6$

Answer: Let $ δ= ε$. If $0 <|x −3| < ε$, then $\left|\dfrac{x^2 −9}{x −3} - 6\right| = \left|\dfrac{(x+3)(x −3)}{x −3} - 6\right| = |x+3 −6|=|x −3| < ε$.

15) $\displaystyle \lim_{x →2}\frac{2x^2 −3x −2}{x −2}=5$

16) $\displaystyle \lim_{x →0}x^4=0$

Answer: Let $ δ=\sqrt[4]{ ε}$. If $0 <|x| <\sqrt[4]{ ε}$, then $\left|x^4-0\right|=x^4 < ε$.

17) $\displaystyle \lim_{x →2}\,(x^2+2x)=8$

In exercises 18 - 20, use the precise definition of limit to prove the given one-sided limits.

18) $\displaystyle \lim_{x →5^ −}\sqrt{5 −x}=0$

Answer: Let $ δ= ε^2$. If $- ε^2 < x - 5 < 0,$ we can multiply through by $-1$ to get $0 <5-x < ε^2.$
Then $\left|\sqrt{5 −x} - 0\right|=\sqrt{5 −x} < \sqrt{ ε^2} = ε$.

19) $\displaystyle \lim_{x →0^+}f(x)= −2$, where $f(x)=\begin{cases}8x −3, & \text{if }x <0\\4x −2, & \text{if }x ≥0\end{cases}$.

20) $\displaystyle \lim_{x →1^ −}f(x)=3$, where $f(x)=\begin{cases}5x −2, & \text{if }x <1\\7x −1, & \text{if }x ≥1\end{cases}$.

Answer: Let $ δ= ε/5$. If $ − ε/5 < x - 1 <0,$ we can multiply through by $-1$ to get $0 <1-x < ε/5.$
Then $|f(x) −3|=|5x-2-3| = |5x −5| = 5(1-x),$ since $x <1$ here.
And $5(1-x) < 5( ε/5) = ε$.

In exercises 21 - 23, use the precise definition of limit to prove the given infinite limits.

21) $\displaystyle \lim_{x →0}\frac{1}{x^2}= ∞$

22) $\displaystyle \lim_{x → −1}\frac{3}{(x+1)^2}= ∞$

Answer: Let $ δ=\sqrt{\frac{3}{N}}$. If $0 <|x+1| <\sqrt{\frac{3}{N}}$, then $f(x)=\frac{3}{(x+1)^2} >N$.

23) $\displaystyle \lim_{x →2} −\frac{1}{(x −2)^2}= − ∞$

24) An engineer is using a machine to cut a flat square of Aerogel of area $144 \,\text{cm}^2$. If there is a maximum error tolerance in the area of $8 \,\text{cm}^2$, how accurately must the engineer cut on the side, assuming all sides have the same length? How do these numbers relate to $ δ$, $ ε$, $a$, and $L$?

Answer: $0.033 \text{ cm}, \, ε=8,\, δ=0.33,\,a=12,\,L=144$

25) Use the precise definition of limit to prove that the following limit does not exist: $\displaystyle \lim_{x →1}\frac{|x −1|}{x −1}.$

26) Using precise definitions of limits, prove that $\displaystyle \lim_{x →0}f(x)$ does not exist, given that $f(x)$ is the ceiling function. (Hint: Try any $ δ <1$.)

Answer: Answers may very.

27) Using precise definitions of limits, prove that $\displaystyle \lim_{x →0}f(x)$ does not exist: $f(x)=\begin{cases}1, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Hint: Think about how you can always choose a rational number $0 <d$, >

28) Using precise definitions of limits, determine $\displaystyle \lim_{x →0}f(x)$ for $f(x)=\begin{cases}x, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Hint: Break into two cases, $x$ rational and $x$ irrational.)

Answer: $0$

29) Using the function from the previous exercise, use the precise definition of limits to show that $\displaystyle \lim_{x →a}f(x)$ does not exist for $a ≠0$

For exercises 30 - 32, suppose that $\displaystyle \lim_{x →a}f(x)=L$ and $\displaystyle \lim_{x →a}g(x)=M$ both exist. Use the precise definition of limits to prove the following limit laws:

30) $\displaystyle \lim_{x →a}(f(x) −g(x))=L −M$

Answer: $f(x) −g(x)=f(x)+( −1)g(x)$

31) $\displaystyle \lim_{x →a}[cf(x)]=cL$ for any real constant $c$ (Hint: Consider two cases: $c=0$ and $c ≠0$.)

32) $\displaystyle \lim_{x →a}[f(x)g(x)]=LM$. (Hint: $|f(x)g(x) −LM|= |f(x)g(x) −f(x)M +f(x)M −LM| ≤|f(x)||g(x) −M| +|M||f(x) −L|.)$

Answer: Answers may vary.

Search

Text Color

Text Size

Margin Size

Font Type