4.8: Multiple Integration (Exercises)
- Page ID
- 83256
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)4.1: Iterated Integrals and Area
In Exercises 1-6, a graph of a planar region \(R\) is given. Give the iterated integrals, with both orders of integration \(dy\,dx\) and \(dx\,dy\), that give the area of \(R\). Evaluate one of the iterated integrals to find the area.
1.
- Answer:
- \(\text{Area} = \displaystyle \quad 9 \,\text{units}^2\)
2.
3.
- Answer:
- \( \text{Area} = \displaystyle \quad 4 \,\text{units}^2\)
4.
5.
- Answer:
- \( \text{Area} = \displaystyle \quad \dfrac{7}{15} \,\text{units}^2\)
6.
In Exercises 7-12, iterated integrals are given that compute the area of a region R in the \(xy\)-plane. Sketch the region R, and give the iterated integral(s) that give the area of R with the opposite order of integration.
7. \(\displaystyle \int_{-2}^2 \int_0^{4-x^2}\,dy\,dx\)
- Answer:
- \(\displaystyle \int_{-2}^2 \int_0^{4-x^2}\,dy\,dx\quad\) \(=\quad \displaystyle \int_{0}^4 \int_{-\sqrt{4-y}}^{\sqrt{4-y}}\,dx\,dy\)
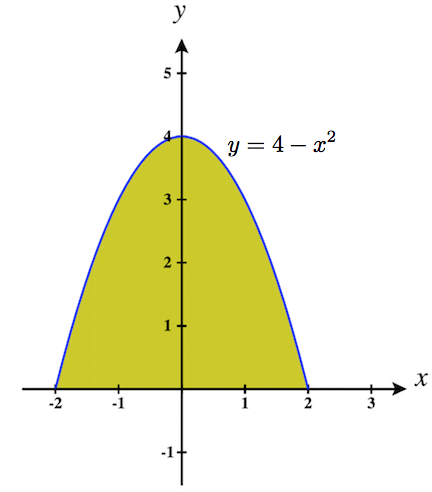
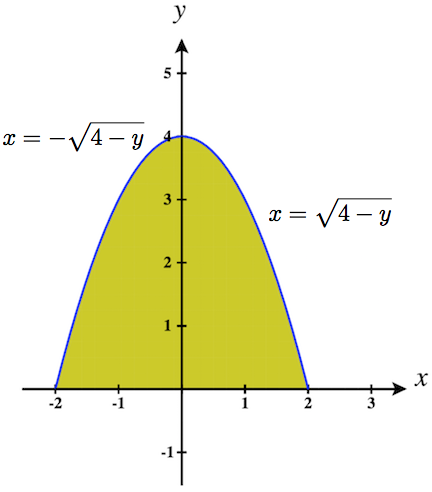
8. \(\displaystyle \int_{0}^1 \int_{5-5x}^{5-5x^2}\,dy\,dx\)
9. \(\displaystyle \int_{-2}^2 \int_0^{2\sqrt{4-y^2}}\,dx\,dy\)
- Answer:
- \(\displaystyle \int_{-2}^2 \int_0^{2\sqrt{4-y^2}}\,dx\,dy\quad\) \(=\quad \displaystyle \int_{0}^4 \int_{-\frac{1}{2}\sqrt{16-x^2}}^{\frac{1}{2}\sqrt{16-x^2}}\,dy\,dx\)
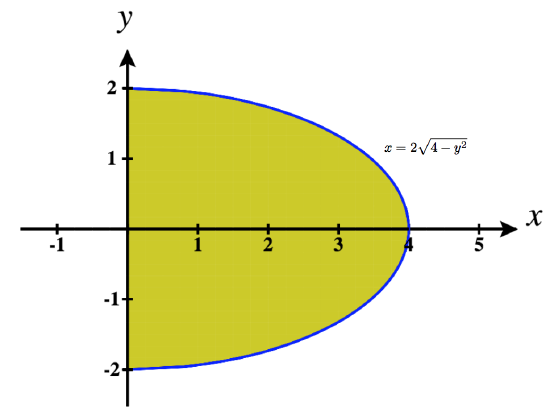
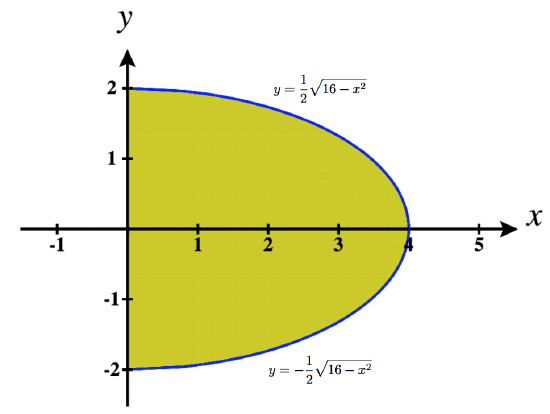
10. \(\displaystyle \int_{-3}^3 \int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}}\,dy\,dx\)
11. \(\displaystyle \int_{0}^1 \int_{-\sqrt{y}}^{\sqrt{y}}\,dx\,dy +\int_1^4 \int_{y-2}^{\sqrt{y}}\,dx\,dy\)
- Answer:
- \(\displaystyle \int_{0}^1 \int_{-\sqrt{y}}^{\sqrt{y}}\,dx\,dy +\int_1^4 \int_{y-2}^{\sqrt{y}}\,dx\,dy \quad\) \(=\quad \displaystyle \int_{-1}^2 \int_{x^2}^{x+2}\,dy\,dx\)
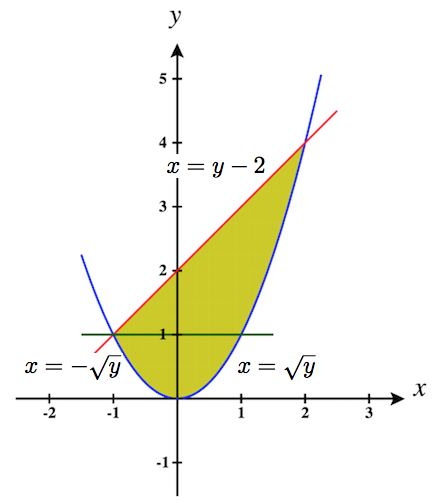
12. \(\displaystyle \int_{-1}^1 \int_{(x-1)/2}^{(1-x)/2}\,dy\,dx\)
In exercises 13 - 18, evaluate the iterated integrals by choosing the order of integration.
13) \(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \sin(2x)\cos(3y)\,dx \space dy\)
- Answer:
- \(0\)
14) \(\displaystyle \int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)]\,dx \space dy\)
15) \(\displaystyle \int_1^e \int_1^e \left[\frac{1}{x}\sin(\ln x) + \frac{1}{y}\cos (\ln y)\right] \,dx \space dy\)
- Answer:
- \((e − 1)(1 + \sin 1 − \cos 1)\)
16) \(\displaystyle \int_1^e \int_1^e \frac{\sin(\ln x)\cos (\ln y)}{xy} \,dx \space dy\)
17) \(\displaystyle \int_1^2 \int_1^2 \left(\frac{\ln y}{x} + \frac{x}{2y + 1}\right)\,dy \space dx\)
- Answer:
- \(\frac{3}{4}\ln \left(\frac{5}{3}\right) + 2 (\ln 2)^2 - \ln 2\)
18) \(\displaystyle \int_0^1 \int_1^2 xe^{x+4y}\,dy \space dx\)
- Answer:
- \(\frac{1}{4}e^4 (e^4 - 1)\)
19. \(\displaystyle \int_{-3}^2 \int_2^5 (6x^2+4xy-3y^2)\,dy\,dx\)
- Answer:
- \(\displaystyle \quad -480\)
20. \(\displaystyle \int_1^2 \int_1^x (x^2y-y+2)\,dy\,dx\)
- Answer:
- \(\displaystyle \quad \dfrac{34}{15}\)
21. \(\displaystyle \int_0^{\pi} \int_0^{y} (\cos x \sin y)\,dx\,dy\)
- Answer:
- \(\displaystyle \quad \dfrac{\pi}{2}\)
In exercises 22 - 25, find the average value of the function over the given rectangles.
22)\(f(x,y) = −x +2y\), \(R = [0,1] \times [0,1]\)
- Answer:
- \(\frac{1}{2}\)
23) \(f(x,y) = x^4 + 2y^3\), \(R = [1,2] \times [2,3]\)
24) \(f(x,y) = \sinh x + \sinh y\), \(R = [0,1] \times [0,2]\)
- Answer:
- \(\frac{1}{2}(2 \space \cosh 1 + \cosh 2 - 3)\).
25) \(f(x,y) = \arctan(xy)\), \(R = [0,1] \times [0,1]\)
4.2: Double Integration and Volume
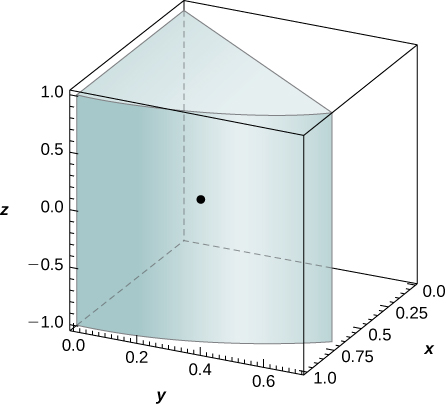
1) The region \(D\) bounded by \(y = x^3, \space y = x^3 + 1, \space x = 0,\) and \(x = 1\) as given in the following figure.
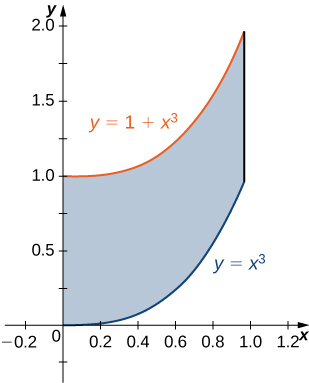
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I but not Type II
b. Find the area of the region \(D\).
c. Find the average value of the function \(f(x,y) = 3xy\) on the region graphed in the previous exercise.
- Answer:
- \(\frac{27}{20}\)
2) The region \(D\) bounded by \(y = \sin x, \space y = 1 + \sin x, \space x = 0\), and \(x = \frac{\pi}{2}\) as given in the following figure.
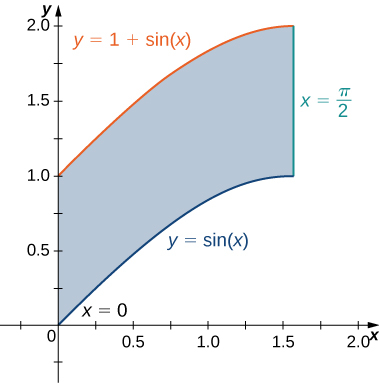
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I but not Type II
b. Find the area of the region \(D\).
- Answer:
- \(\frac{\pi}{2}\, \text{units}^2\)
c. Find the average value of the function \(f(x,y) = \cos x\) on the region \(D\).
3) The region \(D\) bounded by \(x = y^2 - 1\) and \(x = \sqrt{1 - y^2}\) as given in the following figure.
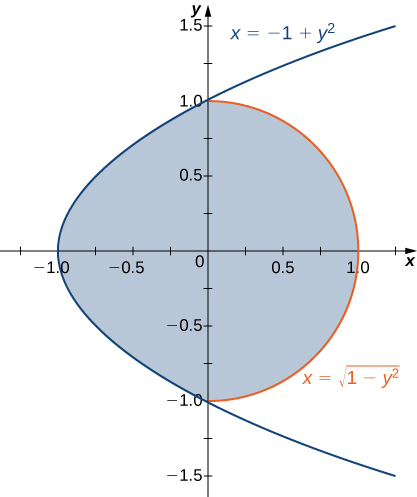
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type II but not Type I
b. Find the volume of the solid under the graph of the function \(f(x,y) = xy + 1\) and above the region \(D\).
- Answer:
- \(\frac{1}{6}(8 + 3\pi)\, \text{units}^3\)
4) The region \(D\) bounded by \(y = 0, \space x = -10 + y,\) and \(x = 10 - y\) as given in the following figure.
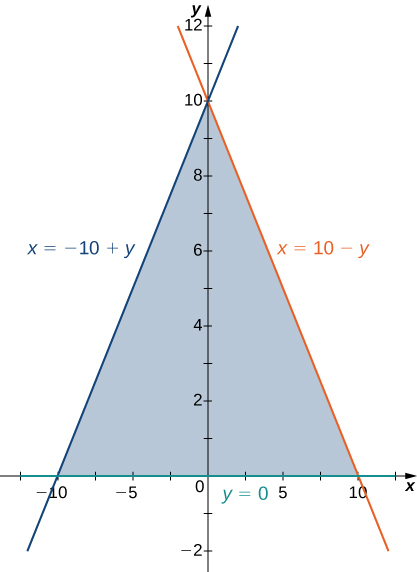
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type II but not Type I
b. Find the volume of the solid under the graph of the function \(f(x,y) = x + y\) and above the region in the figure from the previous exercise.
- Answer:
- \(\frac{1000}{3}\, \text{units}^3\)
5) The region \(D\) bounded by \(y = 0, \space x = y - 1, \space x = \frac{\pi}{2}\) as given in the following figure.
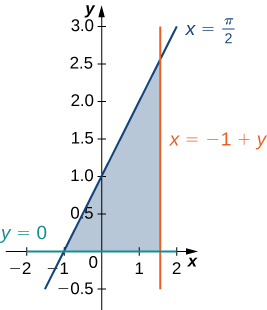
Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I and Type II
6) The region \(D\) bounded by \(y = 0\) and \(y = x^2 - 1\) as given in the following figure.
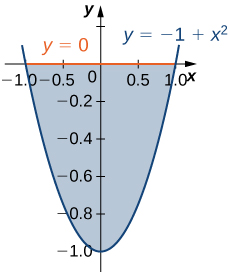
Classify this region as vertically simple (Type I) or horizontally simple (Type II).
- Type:
- Type I and Type II
7) Let \(D\) be the region bounded by the curves of equations \(y = \cos x\) and \(y = 4 - x^2\) and the \(x\)-axis. Explain why \(D\) is neither of Type I nor II.
- Answer:
- The region \(D\) is not of Type I: it does not lie between two vertical lines and the graphs of two continuous functions \(g_1(x)\) and \(g_2(x)\). The region is not of Type II: it does not lie between two horizontal lines and the graphs of two continuous functions \(h_1(y)\) and \(h_2(y)\).
8) Let \(D\) be the region bounded by the curves of equations \(y = x, \space y = -x\) and \(y = 2 - x^2\). Explain why \(D\) is neither of Type I nor II.
In exercises 9 - 14, evaluate the double integral \(\displaystyle \iint_D f(x,y) \,dA\) over the region \(D\). Graph region D.
9) \(f(x,y) = 1\) and
\(D = \big\{(x,y)| \, 0 \leq x \leq \frac{\pi}{2}, \space \sin x \leq y \leq 1 + \sin x \big\}\)
- Answer:
- \(\frac{\pi}{2}\)
10) \(f(x,y) = 2\) and
\(D = \big\{(x,y)| \, 0 \leq y \leq 1, \space y - 1 \leq x \leq \arccos y \big\}\)
11) \(f(x,y) = xy\) and
\(D = \big\{(x,y)| \, -1 \leq y \leq 1, \space y^2 - 1 \leq x \leq \sqrt{1 - y^2} \big\}\)
- Answer:
- \(0\)
12) \(f(x,y) = \sin y\) and \(D\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((3,0)\)
13) \(f(x,y) = -x + 1\) and \(D\) is the triangular region with vertices \((0,0), \space (0,2)\), and \((2,2)\)
- Answer:
- \(\frac{2}{3}\)
14) \(f(x,y) = 2x + 4y\) and
\(D = \big\{(x,y)|\, 0 \leq x \leq 1, \space x^3 \leq y \leq x^3 + 1 \big\}\)
In exercises 15 - 20, evaluate the iterated integrals.
15) \(\displaystyle \int_0^1 \int_{2\sqrt{x}}^{2\sqrt{x}+1} (xy + 1) \,dy \space dx\)
- Answer:
- \(\frac{41}{20}\)
16) \(\displaystyle \int_0^3 \int_{2x}^{3x} (x + y^2) \,dy \space dx\)
17) \(\displaystyle \int_1^2 \int_{-u^2-1}^{-u} (8 uv) \,dv \space du\)
- Answer:
- \(-63\)
18) \(\displaystyle \int_e^{e^2} \int_{\ln u}^2 (v + \ln u) \,dv \space du\)
19) \(\displaystyle \int_0^{1/2} \int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}} 4 \,dx \space dy\)
- Answer:
- \(\pi\)
20) \(\displaystyle \int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} (2x + 4y^3) \,dx \space dy\)
21) Let \(D\) be the region bounded by \(y = 1 - x^2, \space y = 4 - x^2\), and the \(x\)- and \(y\)-axes.
a. Show that \(\displaystyle \iint_D x\,dA = \int_0^1 \int_{1-x^2}^{4-x^2} x \space dy \space dx + \int_1^2 \int_0^{4-x^2} x \space dy \space dx\) by dividing the region \(D\) into two regions of Type I.
b. Evaluate the integral \(\displaystyle \iint_D x \,dA.\)
22) Let \(D\) be the region bounded by \(y = 1, \space y = x, \space y = \ln x\), and the \(x\)-axis.
a. Show that \(\displaystyle \iint_D y^2 \,dA = \int_{-1}^0 \int_{-x}^{2-x^2} y^2 dy \space dx + \int_0^1 \int_x^{2-x^2} y^2 dy \space dx\) by dividing the region \(D\) into two regions of Type I, where \(D = \big\{(x,y)\,|\,y \geq x, y \geq -x, \space y \leq 2-x^2\big\}\).
b. Evaluate the integral \(\displaystyle \iint_D y^2 \,dA.\)
23) Let \(D\) be the region bounded by \(y = x^2\), \(y = x + 2\), and \(y = -x\).
a. Show that \(\displaystyle \iint_D x \, dA = \int_0^1 \int_{-y}^{\sqrt{y}} x \space dx \space dy + \int_1^4 \int_{y-2}^{\sqrt{y}} x \space dx \space dy\) by dividing the region \(D\) into two regions of Type II, where \(D = \big\{(x,y)\,|\,y \geq x^2, \space y \geq -x, \space y \leq x + 2\big\}\).
b. Evaluate the integral \(\displaystyle \iint_D x \,dA.\)
- Answer:
- a. Answers may vary;
b. \(\frac{7}{3}\)
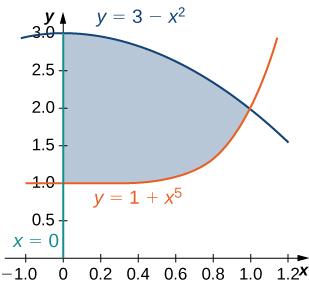
24) The region \(D\) bounded by \(x = 0, y = x^5 + 1\), and \(y = 3 - x^2\) is shown in the following figure. Find the area \(A(D)\) of the region \(D\).
25) The region \(D\) bounded by \(y = \cos x, \space y = 4 + \cos x\), and \(x = \pm \frac{\pi}{3}\) is shown in the following figure. Find the area \(A(D)\) of the region \(D\).
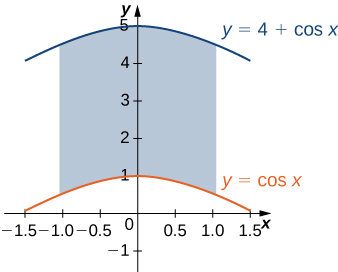
- Answer:
- \(\frac{8\pi}{3}\)
26) Find the area \(A(D)\) of the region \(D = \big\{(x,y)| \, y \geq 1 - x^2, y \leq 4 - x^2, \space y \geq 0, \space x \geq 0 \big\}\).
27) Let \(D\) be the region bounded by \( y = 1, \space y = x, \space y = \ln x\), and the \(x\)-axis. Find the area \(A(D)\) of the region \(D\).
- Answer:
- \(\left(e - \frac{3}{2}\right)\, \text{units}^2\)
28) Find the average value of the function \(f(x,y) = \sin y\) on the triangular region with vertices \((0,0), \space (0,3)\), and \((3,0)\).
29) Find the average value of the function \(f(x,y) = -x + 1\) on the triangular region with vertices \((0,0), \space (0,2)\), and \((2,2)\).
- Answer:
- The average value of \(f\) on this triangular region is \(\frac{1}{3}.\)
In exercises 30 - 33, change the order of integration and evaluate the integral.
30) \(\displaystyle \int_{-1}^{\pi/2} \int_0^{x+1} \sin x \, dy \, dx\)
31) \(\displaystyle \int_0^1 \int_{x-1}^{1-x} x \, dy \, dx\)
- Answer:
- \(\displaystyle \int_0^1 \int_{x-1}^{1-x} x \space dy \space dx = \int_{-1}^0 \int_0^{y+1} x \space dx \space dy + \int_0^1 \int_0^{1-y} x \space dx \space dy = \frac{1}{3}\)
32) \(\displaystyle \int_{-1}^0 \int_{-\sqrt{y+1}}^{\sqrt{y+1}} y^2 dx \space dy\)
33) \(\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy\)
- Answer:
- \(\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy = \int_1^2 \int_{-\sqrt{x^2-1}}^{\sqrt{x^2-1}} y \space dy \space dx = 0\)
34) a. \(\displaystyle \int_{0}^{4} \int_{y}^{4} e^{-x^2} \space dx \space dy\)
b. \(\displaystyle \int_{0}^{4} \int_{\sqrt{x}}^{2} \frac{1}{1+2y^3} \space dy \space dx\)
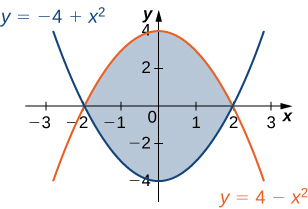
35) The region \(D\) is shown in the following figure. Evaluate the double integral \(\displaystyle \iint_D (x^2 + y) \,dA\) by using the easier order of integration.
36) The region \(D\) is shown in the following figure. Evaluate the double integral \(\displaystyle \iint_D (x^2 - y^2) \,dA\) by using the easier order of integration.
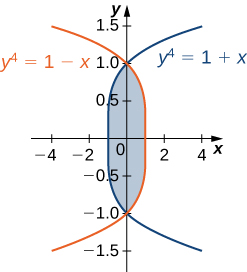
- Answer:
- \(\displaystyle \iint_D (x^2 - y^2) dA = \int_{-1}^1 \int_{y^4-1}^{1-y^4} (x^2 - y^2)dx \space dy = \frac{464}{4095}\)
37) Find the volume of the solid under the surface \(z = 2x + y^2\) and above the region bounded by \(y = x^5\) and \(y = x\).
38) Find the volume of the solid under the plane \(z = 3x + y\) and above the region determined by \(y = x^7\) and \(y = x\).
- Answer:
- \(\frac{4}{5}\, \text{units}^3\)
39) Find the volume of the solid under the plane \(z = 3x + y\) and above the region bounded by \(x = \tan y, \space x = -\tan y\), and \(x = 1\).
40) Find the volume of the solid under the surface \(z = x^3\) and above the plane region bounded by \(x = \sin y, \space x = -\sin y\), and \(x = 1\).
- Answer:
- \(\frac{5\pi}{32}\, \text{units}^3\)
41) Let \(g\) be a positive, increasing, and differentiable function on the interval \([a,b]\). Show that the volume of the solid under the surface \(z = g'(x)\) and above the region bounded by \(y = 0, \space y = g(x), \space x = a\), and \(x = b\) is given by \(\frac{1}{2}(g^2 (b) - g^2 (a))\).
42) Let \(g\) be a positive, increasing, and differentiable function on the interval \([a,b]\) and let \(k\) be a positive real number. Show that the volume of the solid under the surface \(z = g'(x)\) and above the region bounded by \(y = g(x), \space y = g(x) + k, \space x = a\), and \(x = b\) is given by \(k(g(b) - g(a)).\)
43) Find the volume of the solid situated in the first octant and determined by the planes \(z = 2\), \(z = 0, \space x + y = 1, \space x = 0\), and \(y = 0\).
44) Find the volume of the solid situated in the first octant and bounded by the planes \(x + 2y = 1\), \(x = 0, \space z = 4\), and \(z = 0\). Graph the solid and the region of integration.
- Answer:
- \(1\, \text{units}^3\)
45) Find the volume of the solid bounded by the planes \(x + y = 1, \space x - y = 1, \space x = 0, \space z = 0\), and \(z = 10\).
46) Find the volume of the solid bounded by the planes \(x + y = 1, \space x - y = 1, \space x + y = -1\space x - y = -1, \space z = 1\), and \(z = 0\)
- Answer:
- \(2\, \text{units}^3\)
47) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the planes \(x + y + z = 1\) and \(x + y + 2z = 1\) respectively, and let \(S\) be the solid situated between \(S_1, \space S_2, \space x = 0\), and \(y = 0\).
- Find the volume of the solid \(S_1\).
- Find the volume of the solid \(S_2\).
- Find the volume of the solid \(S\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).
48) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the planes \(2x + 2y + z = 2\) and \(x + y + z = 1\) respectively, and let \(S\) be the solid situated between \(S_1, \space S_2, \space x = 0\), and \(y = 0\).
- Find the volume of the solid \(S_1\).
- Find the volume of the solid \(S_2\).
- Find the volume of the solid \(S\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).
- Answer:
- a. \(\frac{1}{3}\, \text{units}^3\)
b. \(\frac{1}{6}\, \text{units}^3\)
c. \(\frac{1}{6}\, \text{units}^3\)
49) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the plane \(x + y + z = 2\) and under the sphere \(x^2 + y^2 + z^2 = 4\), respectively. If the volume of the solid \(S_2\) is \(\frac{4\pi}{3}\) determine the volume of the solid \(S\) situated between \(S_1\) and \(S_2\) by subtracting the volumes of these solids.
50) Let \(S_1\) be the solid situated in the first octant under the plane \(x + y + z = 2\) and and \(S_2\) be the solid situated in the first octant under the plane \(z=2\) and bounded by the cylinder \(x^2 + y^2 = 4\).
- Find the volume of the solid \(S_1\).
- Find the volume of the solid \(S_2\).
- Find the volume of the solid \(S\) situated between \(S_1\) and \(S_2\) by subtracting the volumes of the solids \(S_1\) and \(S_2\). Graph solid S.
- Answer:
- a. \(\frac{4}{3}\, \text{units}^3\)
b. \(2\pi\, \text{units}^3\)
c. \(\frac{6\pi - 4}{3}\, \text{units}^3\)
51) Find the volume of the solid in the first octant bounded by \(z = \sqrt{4 - y^2}\), \(x=2\), \(y=2\). Graph the solid and the region of integration.
Answer: \(2\pi\)
52) Find the volume V of the solid S bounded by the three coordinate planes, bounded above by the plane \(x+y+z=2 \), and bounded below by the plane \(z=x+y\). Graph the solid and the region of integration.
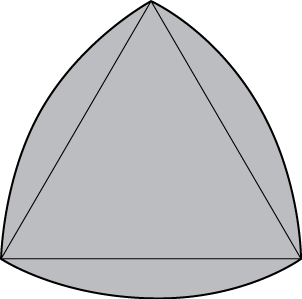
53) [T] The Reuleaux triangle consists of an equilateral triangle and three regions, each of them bounded by a side of the triangle and an arc of a circle of radius s centered at the opposite vertex of the triangle. Show that the area of the Reuleaux triangle in the following figure of side length \(s\) is \(\frac{s^2}{2}(\pi - \sqrt{3})\).
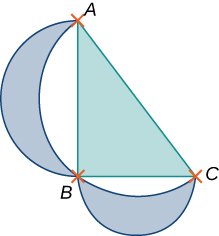
54) [T] Show that the area of the lunes of Alhazen, the two blue lunes in the following figure, is the same as the area of the right triangle \(ABC.\) The outer boundaries of the lunes are semicircles of diameters \(AB\) and \(AC\) respectively, and the inner boundaries are formed by the circumcircle of the triangle \(ABC\).
Terms and Concepts
1. When evaluating \(\displaystyle \int\int_R f(x,y)\,dA\) using polar coordinates, \(f(x,y)\) is replaced with _______ and \(dA\) is replaced with _______.
- Answer:
- \(f(x,y)\) is replaced with \(f(r\cos \theta, r\sin\theta)\) and \(dA\) is replaced with \(r\,dr\,d\theta\).
2. Why would one be interested in evaluating a double integral with polar coordinates?
Defining Polar Regions
In exercises 3 - 6, express the region \(R\) in polar coordinates.
3) \(R\) is the region of the disk of radius 2 centered at the origin that lies in the first quadrant.
- Answer:
- \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 2, \space 0 \leq \theta \leq \frac{\pi}{2}\big\}\)
4) \(R\) is the region of the disk of radius 3 centered at the origin.
5) \(R\) is the region between the circles of radius 4 and radius 5 centered at the origin that lies in the second quadrant.
- Answer:
- \(R = \big\{(r, \theta)\,|\,4 \leq r \leq 5, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\)
6) \(R\) is the region bounded by the \(y\)-axis and \(x = \sqrt{1 - y^2}\).
7) \(R\) is the region bounded by the \(x\)-axis and \(y = \sqrt{2 - x^2}\).
- Answer:
- \(R = \big\{(r, \theta)\,|\,0 \leq r \leq \sqrt{2}, \space 0 \leq \theta \leq \pi\big\}\)
8) \(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4x\big\}\)
9) \(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4y\big\}\)
- Answer:
- \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 4 \space \sin \theta, \space 0 \leq \theta \leq \pi\big\}\)
In exercises 10 - 15, the graph of the polar rectangular region \(D\) is given. Express \(D\) in polar coordinates.
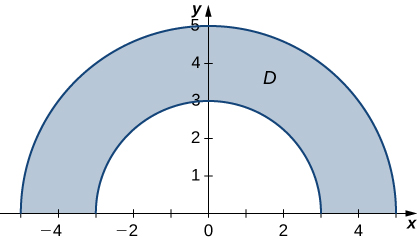
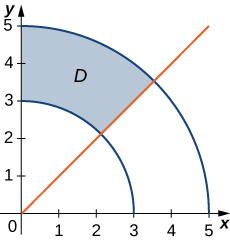
- Answer:
- \(D = \big\{(r, \theta)\,|\, 3 \leq r \leq 5, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}\big\}\)
12)
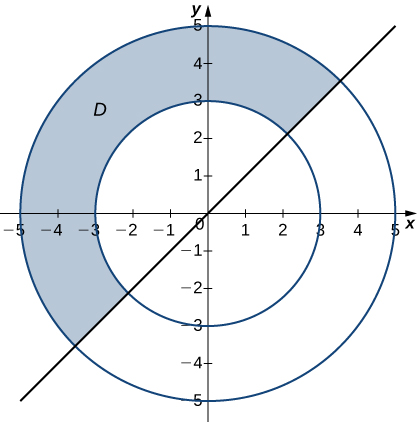
13)
- Answer:
- \(D = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space \frac{3\pi}{4} \leq \theta \leq \frac{5\pi}{4}\big\}\)
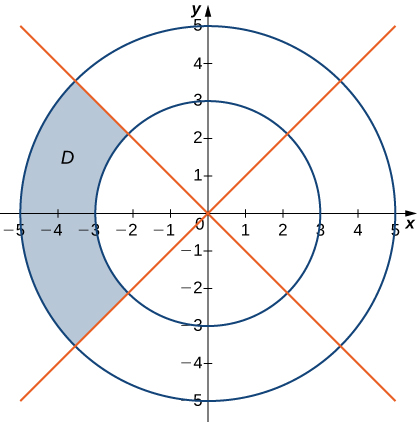
15) In the following graph, the region \(D\) is bounded by \(y = x\) and \(y = x^2\).
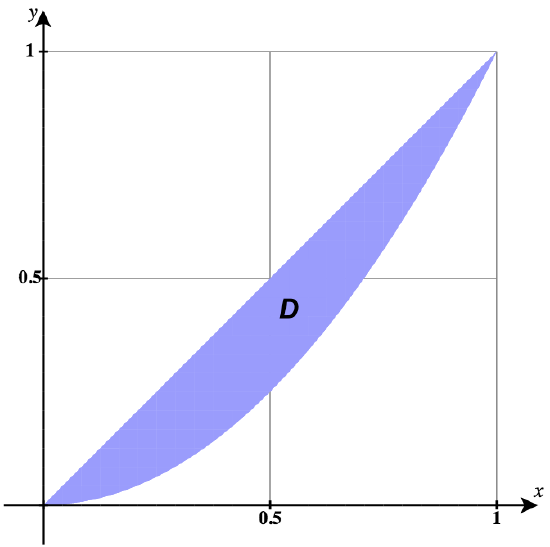
- Answer:
- \(D = \big\{(r, \theta)\,|\,0 \leq r \leq \tan \theta \space \sec \theta, \space 0 \leq \theta \leq \frac{\pi}{4}\big\}\)
Evaluating Polar Double Integrals
In exercises 16 - 25, evaluate the double integral \(\displaystyle \iint_R f(x,y) \,dA\) over the polar rectangular region \(R\).
16) \(f(x,y) = x^2 + y^2\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)
17) \(f(x,y) = x + y\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)
- Answer:
- \(0\)
18) \(f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}\)
19) \(f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}\)
- Answer:
- \(\frac{63\pi}{16}\)
20) \(f(x,y) = \sqrt[3]{x^2 + y^2}\), where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\).
21) \(f(x,y) = x^4 + 2x^2y^2 + y^4\), where \(R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}\).
- Answer:
- \(\frac{3367\pi}{18}\)
22) \(f(x,y) = \sin (\arctan \frac{y}{x})\), where \(R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}\)
23) \(f(x,y) = \arctan \left(\frac{y}{x}\right)\), where \(R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)
- Answer:
- \(\frac{35\pi^2}{576}\)
24) \(\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}\)
25) \(\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)
- Answer:
- \(\frac{7}{576}\pi^2 (21 - e + e^4)\)
Converting Double Integrals to Polar Form
In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.
26) \(\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta\)
27) \(\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta\)
- Answer:
- \(\frac{5}{2} \ln (1 + \sqrt{2})\)
28) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta\)
29) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta\)
- Answer:
- \(\frac{1}{6}(2 - \sqrt{2})\)
In exercises 30 - 37, draw the region of integration, \(R\), labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.
30) \(\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy\)
31) \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy\)
- Answer:
- \(\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}\)
32) \(\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx\)
33) \(\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx\)
- Answer:
- \(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8\)
34) \(\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx\)
35) \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy\)
- Answer:
- \(\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}\)
36) \(\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy\)
37) \(\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx\)
- Answer:
- \(\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}\)
38) Evaluate the integral \(\displaystyle \iint_D r \,dA\) where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).
39) Find the area of the region \(D\) bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).
- Answer:
- \(\frac{3\pi}{4}\)
40) Evaluate the integral \(\displaystyle \iint_D r \,dA,\) where \(D\) is the region bounded by the part of the four-leaved rose \(r = \sin 2\theta\) situated in the first quadrant (see the following figure).
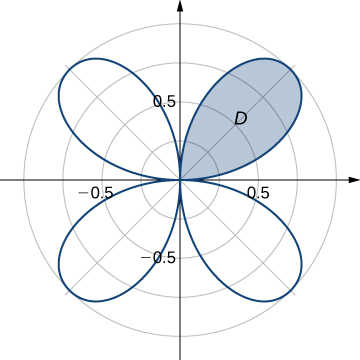
41) Find the total area of the region enclosed by the four-leaved rose \(r = \sin 2\theta\) (see the figure in the previous exercise).
- Answer:
- \(\frac{\pi}{2}\)
42) Find the area of the region \(D\) which is the region bounded by \(y = \sqrt{4 - x^2}\), \(x = \sqrt{3}\), \(x = 2\), and \(y = 0\).
43) Find the area of the region \(D\), which is the region inside the disk \(x^2 + y^2 \leq 4\) and to the right of the line \(x = 1\).
- Answer:
- \(\frac{1}{3}(4\pi - 3\sqrt{3})\)
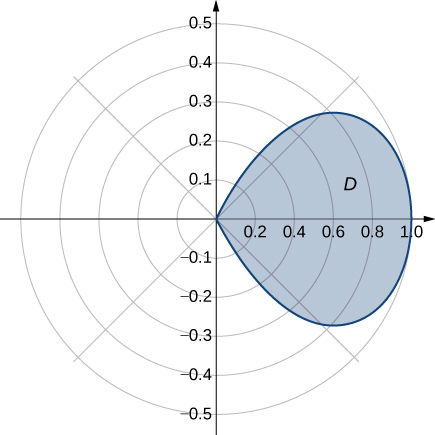
44) Determine the average value of the function \(f(x,y) = x^2 + y^2\) over the region \(D\) bounded by the polar curve \(r = \cos 2\theta\), where \(-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\) (see the following graph).
45) Determine the average value of the function \(f(x,y) = \sqrt{x^2 + y^2}\) over the region \(D\) bounded by the polar curve \(r = 3\sin 2\theta\), where \(0 \leq \theta \leq \frac{\pi}{2}\) (see the following graph).
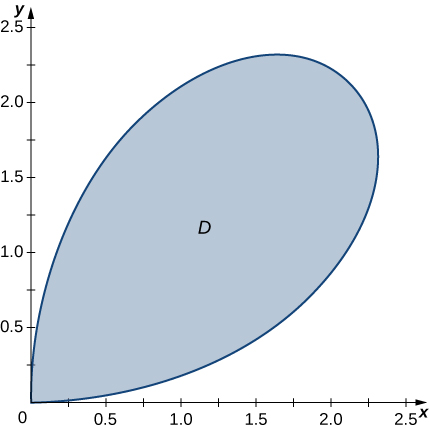
- Answer:
- \(\frac{16}{3\pi}\)
46) Find the volume of the solid situated in the first octant and bounded by the paraboloid \(z = 1 - 4x^2 - 4y^2\) and the planes \(x = 0, \space y = 0\), and \(z = 0\).
47) Find the volume of the solid bounded by the paraboloid \(z = 2 - 9x^2 - 9y^2\) and the plane \(z = 1\).
- Answer:
- \(\frac{\pi}{18}\)
48)
- Find the volume of the solid \(S_1\) bounded by the cylinder \(x^2 + y^2 = 1\) and the planes \(z = 0\) and \(z = 1\).
- Find the volume of the solid \(S_2\) outside the double cone \(z^2 = x^2 + y^2\) inside the cylinder \(x^2 + y^2 = 1\), and above the plane \(z = 0\).
- Find the volume of the solid inside the cone \(z^2 = x^2 + y^2\) and below the plane \(z = 1\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).
49)
- Find the volume of the solid \(S_1\) inside the unit sphere \(x^2 + y^2 + z^2 = 1\) and above the plane \(z = 0\).
- Find the volume of the solid \(S_2\) inside the double cone \((z - 1)^2 = x^2 + y^2\) and above the plane \(z = 0\).
- Find the volume of the solid outside the double cone \((z - 1)^2 = x^2 + y^2\) and inside the sphere \(x^2 + y^2 + z^2 = 1\).
- Answer:
- a. \(\frac{2\pi}{3}\); b. \(\frac{\pi}{3}\); c. \(\frac{\pi}{3}\)
In Exercises 50-51, special double integrals are presented that are especially well suited for evaluation in polar coordinates.
50) The surface of a right circular cone with height \(h\) and base radius \(a\) can be described by the equation \(f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}\), where the tip of the cone lies at \((0,0,h)\) and the circular base lies in the \(xy\)-plane, centered at the origin.
Confirm that the volume of a right circular cone with height \(h\) and base radius \(a\) is \(V=\frac{1}{3}\pi a^2h\) by evaluating \(\displaystyle \int\int_R f(x,y)\,dA\) in polar coordinates.
51) Consider \(\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.\)
(a) Why is this integral difficult to evaluate in rectangular coordinates, regardless of the region \(R\)?
(b) Let \(R\) be the region bounded by the circle of radius \(a\) centered at the origin. Evaluate the double integral using polar coordinates.
(c) Take the limit of your answer from (b), as \(a\to \infty\). What does this imply about the volume under the surface of \(e^{-(x^2+y^2)}\) over the entire \(xy\)-plane?
For the following two exercises, consider a spherical ring, which is a sphere with a cylindrical hole cut so that the axis of the cylinder passes through the center of the sphere (see the following figure).

52) If the sphere has radius 4 and the cylinder has radius 2 find the volume of the spherical ring.
53) A cylindrical hole of diameter 6 cm is bored through a sphere of radius 5 cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.
- Answer:
- \(\frac{256\pi}{3} \space \text{cm}^3\)
54) Find the volume of the solid that lies under the double cone \(z^2 = 4x^2 + 4y^2\), inside the cylinder \(x^2 + y^2 = x\), and above the plane \(z = 0\).
55) Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), inside the cylinder \(x^2 + y^2 = 1\) and above the plane \(z = 0\).
- Answer:
- \(\frac{\pi}{2}\)
56) Find the volume of the solid that lies under the plane \(x + y + z = 10\) and above the disk \(x^2 + y^2 = 4x\).
57) Find the volume of the solid that lies under the plane \(2x + y + 2z = 8\) and above the unit disk \(x^2 + y^2 = 1\).
- Answer:
- \(4\pi\)
58) A radial function \(f\) is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, \(f (x,y) = g(r)\), where \(r = \sqrt{x^2 + y^2}\). Show that if \(f\) is a continuous radial function, then
\[\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r)\] and \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).
59) Use the information from the preceding exercise to calculate the integral \(\displaystyle \iint_D (x^2 + y^2)^3 dA,\) where \(D\) is the unit disk.
- Answer:
- \(\frac{\pi}{4}\)
60) Let \(f(x,y) = \dfrac{F'(r)}{r}\) be a continuous radial function defined on the annular region \(D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), where \(r = \sqrt{x^2 + y^2}\), \(0 < R_1 < R_2\), and \(F\) is a differentiable function.
Show that \(\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].\)
61) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy\) where \(D\) is the annular region between the circles of radii 1 and 2 situated in the third quadrant.
- Answer:
- \(\frac{1}{2} \pi e(e - 1)\)
62) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is, \(f(x,y) = h(\theta)\), where \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).
Show that \(\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]\), where \(H\) is an antiderivative of \(h\).
63) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{y^2}{x^2}\,dA,\) where \(D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.\)
- Answer:
- \(\sqrt{3} - \frac{\pi}{4}\)
64) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is \(f(x,y) = g(r)h(\theta)\), where \((x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\) with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\). Show that \[\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)],\] where \(G\) and \(H\) are antiderivatives of \(g\) and \(h\), respectively.
65) Evaluate \(\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,\) where \(D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\).
- Answer:
- \(\frac{133}{864}\pi^2\)
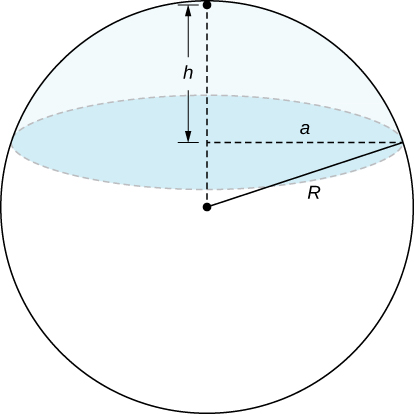
66) A spherical cap is the region of a sphere that lies above or below a given plane.
a. Show that the volume of the spherical cap in the figure below is \(\frac{1}{6} \pi h (3a^2 + h^2)\).
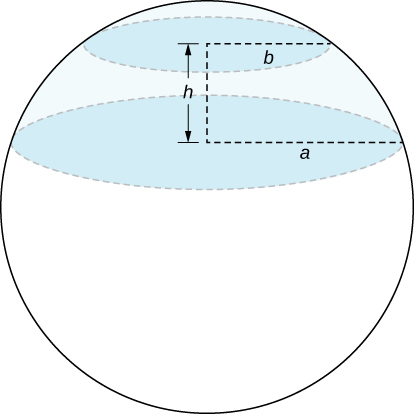
b. A spherical segment is the solid defined by intersecting a sphere with two parallel planes. If the distance between the planes is \(h\) show that the volume of the spherical segment in the figure below is \(\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)\).
67) In statistics, the joint density for two independent, normally distributed events with a mean \(\mu = 0\) and a standard distribution \(\sigma\) is defined by \(p(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}}\). Consider \((X,Y)\), the Cartesian coordinates of a ball in the resting position after it was released from a position on the z-axis toward the \(xy\)-plane. Assume that the coordinates of the ball are independently normally distributed with a mean \(\mu = 0\) and a standard deviation of \(\sigma\) (in feet). The probability that the ball will stop no more than \(a\) feet from the origin is given by \[P[X^2 + Y^2 \leq a^2] = \iint_D p(x,y) dy \space dx,\] where \(D\) is the disk of radius \(a\) centered at the origin. Show that \[P[X^2 + Y^2 \leq a^2] = 1 - e^{-a^2/2\sigma^2}.\]
68) The double improper integral \[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx\] may be defined as the limit value of the double integrals \(\displaystyle \iint_D e^{-x^2+y^2/2}\,dA\) over disks \(D_a\) of radii \(a\) centered at the origin, as \(a\) increases without bound; that is,
\[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}dy \space dx = \lim_{a\rightarrow\infty} \iint_{D_a} e^{-x^2+y^2/2}\,dA.\]
Use polar coordinates to show that \(\displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx = 2\pi.\)
69) Show that \(\displaystyle \int_{-\infty}^{\infty} e^{-x^2/2}\,dx = \sqrt{2\pi}\) by using the relation
\[ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \,dx = \left(\int_{-\infty}^{\infty} e^{-x^2/2}dx \right) \left( \int_{-\infty}^{\infty} e^{-y^2/2}dy \right).\]
Terms and Concepts
1. The strategy for establishing bounds for triple integrals is "from ________ to ________, then from ________ to ________ and then from ________ to ________."
- Answer:
- We integrate from surface to surface, then from curve to curve and then from point to point.
2. Give an informal interpretation of what \(\displaystyle \iiint_Q \,dV\) means.
- Answer:
- \(\displaystyle \iiint_Q \,dV\) = Volume of the solid region \(Q\)
3. Give two uses of triple integration.
- Answer:
- To compute total mass or average density of a solid object, given a density function or to compute the average temperature in a solid region or object.
4. If an object has a constant density \(\delta\) and a volume \(V\), what is its mass?
- Answer:
- It's mass is \(\delta V\).
Volume of Solid Regions
In Exercises 5-8, two surfaces \(f_1(x,y)\) and \(f_2(x,y)\) and a region \(R\) in the \(xy\)-plane are given. Set up and evaluate the triple integral that represents the volume between these surfaces over \(R\).
5. \(f_1(x,y) = 8-x^2-y^2,\,f_2(x,y) =2x+y;\)
\(R\) is the square with corners \((-1,-1)\) and \((1,1)\).
- Answer:
- V = \(\displaystyle \int_{-1}^{1}\int_{-1}^{1}\int_{2x+y}^{8-x^2-y^2} \,dz\,dy\,dx\quad\) \(=\quad\dfrac{88}{3}\,\text{units}^3\)
6. \(f_1(x,y) = x^2+y^2,\,f_2(x,y) =-x^2-y^2;\)
\(R\) is the square with corners \((0,0)\) and \((2,3)\).
7. \(f_1(x,y) = \sin x \cos y,\,f_2(x,y) =\cos x \sin y +2;\)
\(R\) is the triangle with corners \((0,0), \,(\pi , 0)\) and \((\pi,\pi)\).
- Answer:
- V = \(\displaystyle \int_{0}^{\pi}\int_{0}^{x}\int_{\sin x\cos y}^{\cos x\sin y + 2} \,dz\,dy\,dx\quad\) \(=\quad\left(\pi^2 - \pi\right)\,\text{units}^3\quad\) \(\approx 6.72801\,\text{units}^3\)
8. \(f_1(x,y) = 2x^2+2y^2+3,\,f_2(x,y) =6-x^2-y^2;\)
\(R\) is the circle \(x^2+y^2=1\).
In Exercises 9-16, a solid \(D\) is described by its bounding surfaces. Graph the solid. Set up the triple integral that gives the volume of \(D\) in the indicated order(s) of integration. Evaluate the triple integral to find this volume if instructed.
9. \(D\) is bounded by the coordinate planes and \(z=2-\frac{2}{3}x-2y\).
Evaluate the triple integral with order \(dz\,dy\,dx\).
- Answer:
- V = \(\displaystyle \int_{0}^{3}\int_{0}^{1-\frac{x}{3}}\int_{0}^{2 - \frac{2}{3}x-2y} \,dz\,dy\,dx\quad\) \(=\quad 1\,\text{unit}^3\)
10. \(D\) is bounded by the planes \(y=0,y=2,x=1,z=0\) and \(z=(2-x)/2\).
Evaluate the triple integral with order \(dx\,dy\,dz\).
11. \(D\) is bounded by the planes \(x=0,x=2,z=-y\) and by \(z=y^2/2\).
Evaluate the triple integral with orders \(dy\,dz\,dx\) and \(dz\,dy\,dx\) to verify that you obtain the same volume either way.
- Answer:
- V = \(\displaystyle \int_{0}^{2}\int_{0}^{2}\int_{-\sqrt{2z}}^{-z} \,dy\,dz\,dx\quad\) \(=\quad \dfrac{4}{3}\,\text{unit}^3\)
V = \(\displaystyle \int_{0}^{2}\int_{-2}^{0}\int_{\frac{y^2}{2}}^{-y} \,dz\,dy\,dx\quad\) \(=\quad \dfrac{4}{3}\,\text{unit}^3\)
12. \(D\) is bounded by the planes \(y=0,y=9, x=0\) and by \(z=\sqrt{y^2-9x^2}\).
Do not evaluate any triple integral. Just set this one up.
13. \(D\) is bounded by the planes \(x=2,y=1,z=0\) and \(z=2x+4y-4\).
Evaluate the triple integral with orders \(dz\,dy\,dx\) and \(dx\,dy\,dz\) to verify that you obtain the same volume either way.
- Answer:
- V = \(\displaystyle \int_{0}^{2}\int_{1-\frac{x}{2}}^{1}\int_{0}^{2x+4y-4} \,dz\,dy\,dx\quad\) \(=\quad\dfrac{4}{3}\,\text{units}^3\)
V = \(\displaystyle \int_{0}^{4}\int_{\frac{z}{4}}^{1}\int_{(z-4y+4)/2}^{2} \,dx\,dy\,dz\quad\) \(=\quad\dfrac{4}{3}\,\text{units}^3\)
14. \(D\) is bounded by the plane \(z=2y\) and by \(y=4-x^2\).
Evaluate the triple integral with order \(dz\,dy\,dx\).
15. \(D\) is bounded by the coordinate planes and \(y=1-x^2\) and \(y=1-z^2\).
Do not evaluate any triple integral. Which order would be easier to evaluate: \(dz\,dy\,dx\) or \(dy\,dz\,dx\)? Explain why.
- Answer:
- V = \(\displaystyle \int_{0}^{1}\int_{0}^{1-x^2}\int_{0}^{\sqrt{1-y}} \,dz\,dy\,dx\quad\)
V = \(\displaystyle \int_{0}^{1}\int_{0}^{x}\int_{0}^{1-x^2} \,dy\,dz\,dx + \displaystyle \int_{0}^{1}\int_{x}^{1}\int_{0}^{1-z^2} \,dy\,dz\,dx\)
The first one is easier since it only requires evaluation of a single integral, although both can be evaluated fairly easily.
16. \(D\) is bounded by the coordinate planes and by \(z=1-y/3\) and \(z=1-x\).
Evaluate the triple integral with order \(dx\,dy\,dz\).
Evaluating General Triple Integrals
In exercises 17 - 20, evaluate the triple integrals over the rectangular solid box \(B\).
17. \(\displaystyle \iiint_B (2x + 3y^2 + 4z^3) \space dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 2, \space 0 \leq z \leq 3\big\}\)
- Answer:
- \(192\)
18. \(\displaystyle \iiint_B (xy + yz + xz) \space dV,\) where \(B = \big\{(x,y,z) \,|\, 1 \leq x \leq 2, \space 0 \leq y \leq 2, \space 1 \leq z \leq 3\big\}\)
19. \(\displaystyle \iiint_B (x \space cos \space y + z) \space dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq \pi, \space -1 \leq z \leq 1\big\}\)
- Answer:
- \(0\)
20. \(\displaystyle \iiint_B (z \space sin \space x + y^2) \space dV,\) where \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq \pi, \space 0 \leq y \leq 1, \space -1 \leq z \leq 2\big\}\)
In Exercises 21 - 24, evaluate the triple integral.
21. \(\displaystyle \int_{-\pi/2}^{\pi/2}\int_{0}^{\pi}\int_{0}^{\pi} (\cos x \sin y \sin z )\,dz\,dy\,dx\)
- Answer:
- \(8\)
22. \(\displaystyle \int_{0}^{1}\int_{0}^{x}\int_{0}^{x+y} (x+y+z )\,dz\,dy\,dx\)
23. \(\displaystyle \int_{0}^{\pi}\int_{0}^{1}\int_{0}^{z} (\sin (yz))\,dx\,dy\,dz\)
- Answer:
- \(\pi\)
24. \(\displaystyle \int_{\pi}^{\pi^2}\int_{x}^{x^3}\int_{-y^2}^{y^2} (\cos x \sin y \sin z )\,dz\,dy\,dx\)
Average Value of a Function
25. Find the average value of the function \(f(x,y,z) = x + y + z\) over the parallelepiped determined by \(x = 0, \space x = 1, \space y = 0, \space y = 3, \space z = 0\), and \(z = 5\).
- Answer:
- \(\frac{9}{2}\)
26. Find the average value of the function \(f(x,y,z) = xyz\) over the solid \(E = [0,1] \times [0,1] \times [0,1]\) situated in the first octant.
Approximating Triple Integrals
27. The midpoint rule for the triple integral \(\displaystyle \iiint_B f(x,y,z) \,dV\) over the rectangular solid box \(B\) is a generalization of the midpoint rule for double integrals. The region \(B\) is divided into subboxes of equal sizes and the integral is approximated by the triple Riemann sum \[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\bar{x_i}, \bar{y_j}, \bar{z_k}) \Delta V,\nonumber\] where \((\bar{x_i}, \bar{y_j}, \bar{z_k})\) is the center of the box \(B_{ijk}\) and \(\Delta V\) is the volume of each subbox. Apply the midpoint rule to approximate \[\iiint_B x^2 \,dV\nonumber\] over the solid \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 1, \space 0 \leq z \leq 1 \big\}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.
- Answer:
- \(\displaystyle \iiint_B f(x,y,z) \,dV\quad\) \(\approx\quad\frac{5}{16} \approx 0.313\)
28. [T] a. Apply the midpoint rule to approximate \[\iiint_B e^{-x^2} \,dV\nonumber\] over the solid \(B = \{(x,y,z) | 0 \leq x \leq 1, \space 0 \leq y \leq 1, \space 0 \leq z \leq 1 \}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.
b. Use a CAS to improve the above integral approximation in the case of a partition of \(n^3\) cubes of equal size, where \(n = 3,4, ..., 10\).
Applications
29. Suppose that the temperature in degrees Celsius at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T (x,y,z) = xz + 5z + 10\nonumber\] Find the average temperature over the solid.
- Answer:
- \(17.5^{\circ}\) C
30. Suppose that the temperature in degrees Fahrenheit at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T(x,y,z) = x + y + xy\nonumber\] Find the average temperature over the solid.
31. If the charge density at an arbitrary point \((x,y,z)\) of a solid \(E\) is given by the function \(\rho (x,y,z)\), then the total charge inside the solid is defined as the triple integral \(\displaystyle \iiint_E \rho (x,y,z) \,dV.\) Assume that the charge density of the solid \(E\) enclosed by the paraboloids \(x = 5 - y^2 - z^2\) and \(x = y^2 + z^2 - 5\) is equal to the distance from an arbitrary point of \(E\) to the origin. Set up the integral that gives the total charge inside the solid \(E\).
- Answer:
- Total Charge inside the Solid \(E \quad=\quad\) \(\displaystyle \int_{-\sqrt{5}}^{\sqrt{5}}\int_{-\sqrt{5-y^2}}^{\sqrt{5-y^2}}\int_{y^2+z^2-5}^{5 - y^2 - z^2} \sqrt{x^2+y^2+z^2}\,dx\,dz\,dy\)
32. Show that the volume of a regular right hexagonal pyramid of edge length \(a\) is \(\dfrac{a^3 \sqrt{3}}{2}\) by using triple integrals.
In exercises 1 - 8, evaluate the triple integrals \(\displaystyle \iiint_E f(x,y,z) \, dV\) over the solid \(E\).
1. \(f(x,y,z) = z, \quad E = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 9, \quad x \leq 0, \quad y \leq 0, \quad 0 \leq z \leq 1\big\}\)
- Answer:
- \(\frac{9\pi}{8}\)
2. \(f(x,y,z) = xz^2, \space E = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 16, \space x \geq 0, \space y \leq 0, \space -1 \leq z \leq 1\big\}\)
3. \(f(x,y,z) = xy, \space E = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 1, \space x \geq 0, \space x \geq y, \space -1 \leq z \leq 1\big\}\)
- Answer:
- \(-\frac{1}{8}\)
4. \(f(x,y,z) = x^2 + y^2, \space E = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 4, \space x \geq 0, \space x \leq y, \space 0 \leq z \leq 3\big\}\)
5. \(f(x,y,z) = e^{\sqrt{x^2+y^2}}, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 4, \space y \leq 0, \space x \leq y\sqrt{3}, \space 2 \leq z \leq 3 \big\}\)
- Answer:
- \(\frac{\pi e^2}{6}\)
6. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 9, \space y \leq 0, \space 0 \leq z \leq 1\big\}\)
7. a. Let \(B\) be a cylindrical shell with inner radius \(a\) outer radius \(b\), and height \(c\) where \(0 < a < b\) and \(c>0\). Assume that a function \(F\) defined on \(B\) can be expressed in cylindrical coordinates as \(F(x,y,z) = f(r) + h(z)\), where \(f\) and \(h\) are differentiable functions. If \(\displaystyle \int_a^b \bar{f} (r) \,dr = 0\) and \(\bar{h}(0) = 0\), where \(\bar{f}\) and \(\bar{h}\) are antiderivatives of \(f\) and \(h\), respectively, show that \(\displaystyle \iiint_B F(x,y,z) \,dV = 2\pi c (b\bar{f} (b) - a \bar{f}(a)) + \pi(b^2 - a^2) \bar{h} (c).\)
b. Use the previous result to show that \( \displaystyle \iiint_B \left(z + \sin \sqrt{x^2 + y^2}\right) \,dx \space dy \space dz = 6 \pi^2 ( \pi - 2),\) where \(B\) is a cylindrical shell with inner radius \(\pi\) outer radius \(2\pi\), and height \(2\).
8. a. Let \(B\) be a cylindrical shell with inner radius \(a\) outer radius \(b\) and height \(c\) where \(0 < a < b\) and \(c > 0\). Assume that a function \(F\) defined on \(B\) can be expressed in cylindrical coordinates as \(F(x,y,z) = f(r) g(\theta) f(z)\), where \(f, \space g,\) and \(h\) are differentiable functions. If \(\displaystyle\int_a^b \tilde{f} (r) \, dr = 0,\) where \(\tilde{f}\) is an antiderivative of \(f\), show that \(\displaystyle\iiint_B F (x,y,z)\,dV = [b\tilde{f}(b) - a\tilde{f}(a)] [\tilde{g}(2\pi) - \tilde{g}(0)] [\tilde{h}(c) - \tilde{h}(0)],\) where \(\tilde{g}\) and \(\tilde{h}\) are antiderivatives of \(g\) and \(h\), respectively.
b. Use the previous result to show that \(\displaystyle\iiint_B z \sin \sqrt{x^2 + y^2} \,dx \space dy \space dz = - 12 \pi^2,\) where \(B\) is a cylindrical shell with inner radius \(\pi\) outer radius \(2\pi\), and height \(2\).
In exercises 9 - 12, the boundaries of the solid \(E\) are given in cylindrical coordinates.
a. Graph solid E
b. Express the region \(E\) in cylindrical coordinates.
c. Convert the integral \(\displaystyle \iiint_E f(x,y,z) \,dV\) to cylindrical coordinates.
9. \(E\) is bounded by the right circular cylinder \(r = 4 \sin \theta\), the \(r\theta\)-plane, and the sphere \(r^2 + z^2 = 16\).
- Answer:
-
a. \(E = \big\{(r,\theta,z)\, | \,0 \leq \theta \leq \pi, \space 0 \leq r \leq 4 \sin \theta, \space 0 \leq z \leq \sqrt{16 - r^2}\big\}\)
b. \(\displaystyle\int_0^{\pi} \int_0^{4 \sin \theta} \int_0^{\sqrt{16-r^2}} f(r,\theta, z) r \, dz \space dr \space d\theta\)
10. \(E\) is bounded by the right circular cylinder \(r = \cos \theta\), the \(r\theta\)-plane, and the sphere \(r^2 + z^2 = 9\).
11. \(E\) is located in the first octant and is bounded by the circular paraboloid \(z = 9 - 3r^2\), the cylinder \(r = \sqrt{3}\), and the plane \(r(\cos \theta + \sin \theta) = 20 - z\).
- Answer:
-
a. \(E = \big\{(r,\theta,z) \, | \, 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq r \leq \sqrt{3}, \space 9 - r^2 \leq z \leq 10 - r(\cos \theta + \sin \theta)\big\}\)
b. \(\displaystyle\int_0^{\pi/2} \int_0^{\sqrt{3}} \int_{9-r^2}^{10-r(\cos \theta + \sin \theta)} f(r,\theta,z) r \space dz \space dr \space d\theta\)
12. \(E\) is located in the first octant outside the circular paraboloid \(z = 10 - 2r^2\) and inside the cylinder \(r = \sqrt{5}\) and is bounded also by the planes \(z = 20\) and \(\theta = \frac{\pi}{4}\).
In exercises 13 - 16, the function \(f\) and solid \(E\) are given.
a. Graph solid E
b. Express the solid \(E\) and the function \(f\) in cylindrical coordinates.
c. Convert the integral \(\displaystyle \iiint_E f(x,y,z) \,dV\) into cylindrical coordinates and evaluate it.
13. \(f(x,y,z) = x^2 + y^2\), \(E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 \leq 9, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x + 3\big\}\)
- Answer:
-
c. \( \frac{3^5}{5}+\frac{3^5 \pi}{8}\)
14. \(f(x,y,z) = x^2 + y^2, \space E = \big\{(x,y,z) |0 \leq x^2 + y^2 \leq 4, \space y \geq 0, \space 0 \leq z \leq 3 - x \big\}\)
15. \(f(x,y,z) = x, \space E = \big\{(x,y,z)\, | \,1 \leq y^2 + z^2 \leq 9, \space 0 \leq x \leq 1 - y^2 - z^2\big\}\)
- Answer:
-
a. \(y = r \space \cos \theta, \space z = r \space \sin \theta, \space x = z,\space E = \big\{(r,\theta,z)\, | \,1 \leq r \leq 3, \space 0 \leq \theta \leq 2\pi, \space 0 \leq z \leq 1 - r^2\big\}, \space f(r,\theta,z) = z\);
b. \(\displaystyle \int_1^3 \int_0^{2\pi} \int_0^{1-r^2} z r \space dz \space d\theta \space dr = \frac{356 \pi}{3}\)
16. \(f(x,y,z) = y, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + z^2 \leq 9, \space 0 \leq y \leq 1 - x^2 - z^2 \big\}\)
In exercises 17 - 24, find the volume of the solid \(E\) whose boundaries are given in rectangular coordinates. Graph solid E.
17. \(E\) is above the \(xy\)-plane, inside the cylinder \(x^2 + y^2 = 1\), and below the plane \(z = 1\).
- Answer:
- \(\pi\)
18. \(E\) is below the plane \(z = 1\) and inside the paraboloid \(z = x^2 + y^2\).
19. \(E\) is bounded by the circular cone \(z = \sqrt{x^2 + y^2}\) and \(z = 1\).
- Answer:
- \(\frac{\pi}{3}\)
20. \(E\) is located above the \(xy\)-plane, below \(z = 1\), outside the one-sheeted hyperboloid \(x^2 + y^2 - z^2 = 1\), and inside the cylinder \(x^2 + y^2 = 2\).
21. \(E\) is bounded by \(z = 1 - x^2 - y^2\) and \(z = x^2 + y^2\).
- Answer:
- \(\frac{\pi}{4}\)
22. \(E\) is located inside the sphere \(x^2 + y^2 + z^2 = 1\), above the \(xy\)-plane, and inside the circular cone \(z = \sqrt{x^2 + y^2}\).
23. \(E\) is located outside the circular cone \(x^2 + y^2 = (z - 1)^2\) and inside the right circular cylinder \(x^2 + y^2 = 1\).
- Answer:
- \(\frac{4\pi}{3}\)
24. \(E\) is located outside the circular cone \(z = 1 - \sqrt{x^2 + y^2}\), above the \(xy\)-plane, below the circular paraboloid, and between the planes \(z = 0\) and \(z = 2\).
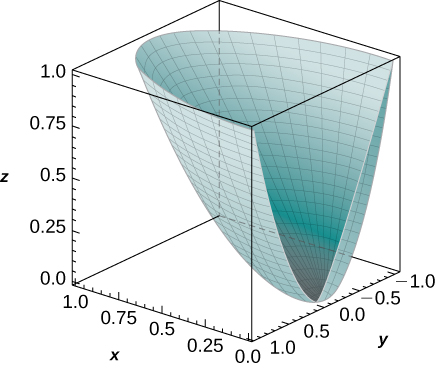
25. [T] Use a computer algebra system (CAS) to graph the solid whose volume is given by the iterated integral in cylindrical coordinates \(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^1 \int_{r^2}^r r \, dz \, dr \, d\theta.\) Find the volume \(V\) of the solid. Round your answer to four decimal places.
- Answer:
-
\(V = \frac{pi}{12} \approx 0.2618\)
26. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates \(\displaystyle \int_0^{\pi/2} \int_0^1 \int_{r^4}^r r \, dz \, dr \, d\theta.\) Find the volume \(E\) of the solid. Round your answer to four decimal places.
27. Convert the integral \(\displaystyle\int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \space dz \space dx \space dy\) into an integral in cylindrical coordinates.
- Answer:
- \(\displaystyle\int_0^1 \int_0^{\pi} \int_{r^2}^r zr^2 \space \cos \theta \, dz \space d\theta \space dr\)
28. Convert the integral \(\displaystyle \int_0^2 \int_0^y \int_0^1 (xy + z) \, dz \space dx \space dy\) into an integral in cylindrical coordinates.
In exercises 29 - 32, evaluate the triple integral \(\displaystyle \iiint_B f(x,y,z) \,dV\) over the solid \(B\).
29. \(f(x,y,z) = 1, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 90, \space z \geq 0\big\}\)
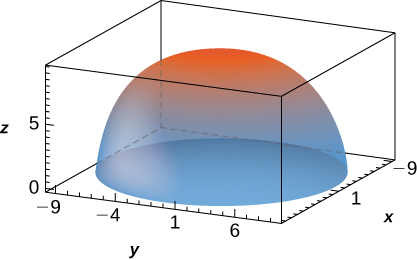
[Hide Solution]
- Answer:
- \(180 \pi \sqrt{10}\)
30. \(f(x,y,z) = 1 - \sqrt{x^2 + y^2 + z^2}, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 9, \space y \geq 0, \space z \geq 0\big\}\)
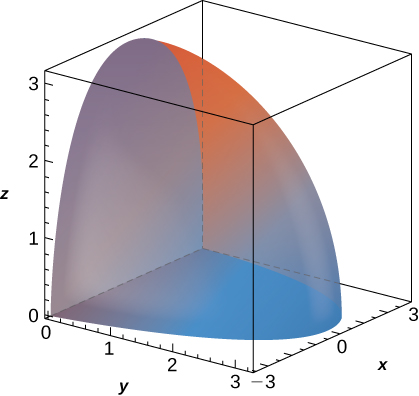
31. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 9\) with \(z \geq 0\) and below by the cone \(3z^2 = x^2 + y^2\).
- Answer:
- \(\frac{81}{4}\pi(\frac{\pi}{3} - \frac{\sqrt{3}}{4})\)
32. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 16\) with \(z \geq 0\) and below by the cone \(2z^2 = x^2 + y^2\).
33. Show that if \(F ( \rho,\theta,\varphi) = f(\rho)g(\theta)h(\varphi)\) is a continuous function on the spherical box \(B = \big\{(\rho,\theta,\varphi)\, | \,a \leq \rho \leq b, \space \alpha \leq \theta \leq \beta, \space \gamma \leq \varphi \leq \psi\big\}\), then \(\displaystyle\iiint_B F \space dV = \left(\int_a^b \rho^2 f(\rho) \space dr \right) \left( \int_{\alpha}^{\beta} g (\theta) \space d\theta \right)\left( \int_{\gamma}^{\psi} h (\varphi) \space \sin \varphi \space d\varphi \right).\)
34. A function \(F\) is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as \(F(x,y,z) = f(\rho)\), where \(\rho = \sqrt{x^2 + y^2 + z^2}\). Show that \(\displaystyle\iiint_B F(x,y,z) \,dV = 2\pi \int_a^b \rho^2 f(\rho) \,d\rho,\) where \(B\) is the region between the upper concentric hemispheres of radii \(a\) and \(b\) centered at the origin, with \(0 < a < b\) and \(F\) a spherical function defined on \(B\).
Use the previous result to show that \(\displaystyle\iiint_B (x^2 + y^2 + z^2) \sqrt{x^2 + y^2 + z^2} dV = 21 \pi,\) where \(B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0\big\}\).
35. Let \(B\) be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where \(0 < a < b\). Consider F a function defined on B whose form in spherical coordinates \((\rho,\theta,\varphi)\) is \(F(x,y,z) = f(\rho)\cos \varphi\). Show that if \(g(a) = g(b) = 0\) and \(\displaystyle\int_a^b h (\rho) \, d\rho = 0,\) then \(\displaystyle\iiint_B F(x,y,z)\,dV = \frac{\pi^2}{4} [ah(a) - bh(b)],\) where \(g\) is an antiderivative of \(f\) and \(h\) is an antiderivative of \(g\).
Use the previous result to show that \(\displaystyle \iiint_B = \frac{z \cos \sqrt{x^2 + y^2 + z^2}}{\sqrt{x^2 + y^2 + z^2}} \, dV = \frac{3\pi^2}{2},\) where \(B\) is the region between the upper concentric hemispheres of radii \(\pi\) and \(2\pi\) centered at the origin and situated in the first octant.
In exercises 36 - 39, the function \(f\) and region \(E\) are given.
a. Express the region \(E\) and function \(f\) in cylindrical coordinates.
b. Convert the integral \(\displaystyle \iiint_B f(x,y,z)\, dV\) into cylindrical coordinates and evaluate it.
36. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 + z^2 \leq 1, \space z \geq 0\big\}\)
37. \(f(x,y,z) = x + y; \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0, \space y \geq 0\big\}\)
- Answer:
-
a. \(f(\rho,\theta, \varphi) = \rho \space \sin \varphi \space (\cos \theta + \sin \theta), \space E = \big\{(\rho,\theta,\varphi)\, | \,1 \leq \rho \leq 2, \space 0 \leq \theta \leq \pi, \space 0 \leq \varphi \leq \frac{\pi}{2}\big\}\);
b. \(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \int_1^2 \rho^3 \cos \varphi \space \sin \varphi \space d\rho \space d\varphi \space d\theta = \frac{15\pi}{8}\)
38. \(f(x,y,z) = 2xy; \space E = \big\{(x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{1 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)
39. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 - 2x \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)
- Answer:
-
a. \(f(\rho,\theta,\varphi) = \rho \space \cos \varphi; \space E = \big\{(\rho,\theta,\varphi)\, | \,0 \leq \rho \leq 2 \space \cos \varphi, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq \varphi \leq \frac{\pi}{4}\big\}\);
b. \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/4} \int_0^{2 \space \cos \varphi} \rho^3 \sin \varphi \space \cos \varphi \space d\rho \space d\varphi \space d\theta = \frac{7\pi}{24}\)
In exercises 40 - 41, find the volume of the solid \(E\) whose boundaries are given in rectangular coordinates.
40. \(E = \big\{ (x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{16 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)
41. \(E = \big\{ (x,y,z)\, | \,x^2 + y^2 + z^2 - 2z \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)
- Answer:
- \(\frac{\pi}{4}\)
42. Use spherical coordinates to find the volume of the solid situated outside the sphere \(\rho = 1\) and inside the sphere \(\rho = \cos \varphi\), with \(\varphi \in [0,\frac{\pi}{2}]\).
43. Use spherical coordinates to find the volume of the ball \(\rho \leq 3\) that is situated between the cones \(\varphi = \frac{\pi}{4}\) and \(\varphi = \frac{\pi}{3}\).
- Answer:
- \(9\pi (\sqrt{2} - 1)\)
44. Convert the integral \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2) \, dz \, dx \, dy\) into an integral in spherical coordinates.
45. Convert the integral \(\displaystyle \int_0^4 \int_0^{\sqrt{16-x^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^2 \, dz \space dy \space dx\) into an integral in spherical coordinates.
- Answer:
- \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/2} \int_0^4 \rho^6 \sin \varphi \, d\rho \, d\phi \, d\theta\)
47. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates \(\displaystyle \int_{\pi/2}^{\pi} \int_{5\pi}^{\pi/6} \int_0^2 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Find the volume \(V\) of the solid. Round your answer to three decimal places.
- Answer:
-
\(V = \frac{4\pi\sqrt{3}}{3} \approx 7.255\)
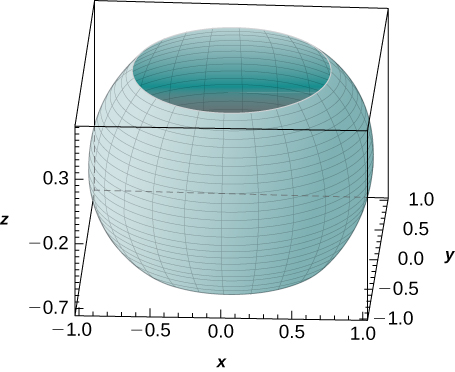
48. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates as \(\displaystyle \int_0^{2\pi} \int_{3\pi/4}^{\pi/4} \int_0^1 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Find the volume \(V\) of the solid. Round your answer to three decimal places.
49. [T] Use a CAS to evaluate the integral \(\displaystyle \iiint_E (x^2 + y^2) \, dV\) where \(E\) lies above the paraboloid \(z = x^2 + y^2\) and below the plane \(z = 3y\).
- Answer:
- \(\frac{343\pi}{32}\)
50. [T]
a. Evaluate the integral \(\displaystyle \iiint_E e^{\sqrt{x^2+y^2+z^2}}\, dV,\) where \(E\) is bounded by spheres \(4x^2 + 4y^2 + 4z^2 = 1\) and \(x^2 + y^2 + z^2 = 1\).
b. Use a CAS to find an approximation of the previous integral. Round your answer to two decimal places.
51. Express the volume of the solid inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the cylinder \(x^2 + y^2 = 4\) as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
- Answer:
- \(\displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ\) and \(\displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi\)
52. Express the volume of the solid inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the cylinder \(x^2 + y^2 = 4\) that is located in the first octant as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
53. The power emitted by an antenna has a power density per unit volume given in spherical coordinates by \(p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} \cos^2 \theta \space \sin^4 \varphi\), where \(P_0\) is a constant with units in watts. The total power within a sphere \(B\) of radius \(r\) meters is defined as \(\displaystyle P = \iiint_B p(\rho,\theta,\varphi) \, dV.\) Find the total power \(P\).
- Answer:
- \(P = \frac{32P_0 \pi}{3}\) watts
54. Use the preceding exercise to find the total power within a sphere \(B\) of radius 5 meters when the power density per unit volume is given by \(p(\rho, \theta,\varphi) = \frac{30}{\rho^2} \cos^2 \theta \sin^4 \varphi\).
55. A charge cloud contained in a sphere \(B\) of radius \(r\) centimeters centered at the origin has its charge density given by \(q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}\), where \(k > 0\). The total charge contained in \(B\) is given by \(\displaystyle Q = \iiint_B q(x,y,z) \, dV.\) Find the total charge \(Q\).
- Answer:
- \(Q = kr^4 \pi \mu C\)
56. Use the preceding exercise to find the total charge cloud contained in the unit sphere if the charge density is \(q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}\).
In exercises 1 - 12, the region \(R\) occupied by a lamina is shown in a graph. Find the mass of \(R\) with the density function \(\rho\).
1. \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
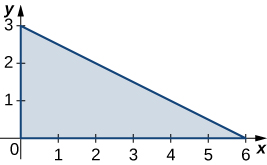
- Answer:
- \(\frac{27}{2}\)
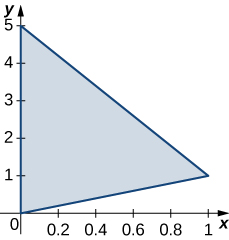
2. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
3. \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3) \) and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
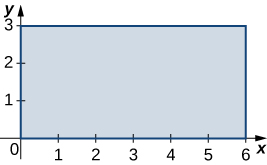
- Answer:
- \(24\sqrt{2}\)
4. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\) and \( (3,1); \space \rho (x,y) = x^2y\).
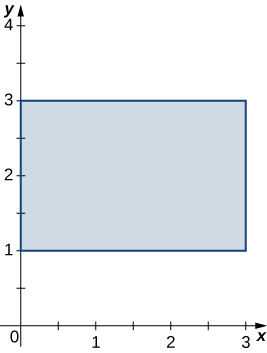
5. \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and \(x = 0; \space \rho (x,y) = 3xy\).
- Answer:
- \(76\)
6. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\) and \(y = -x + 3; \space \rho (x,y) = 2x + y\).
7. \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
- Answer:
- \(8\pi\)
8. \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
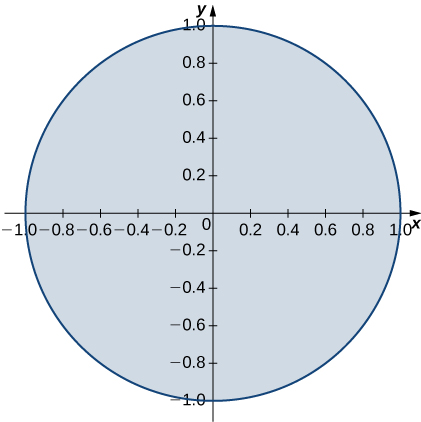
9. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
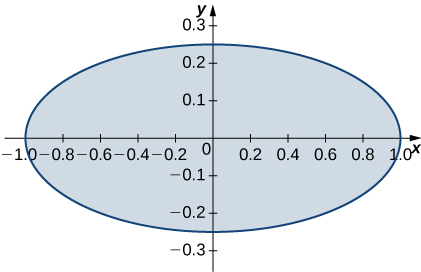
- Answer:
- \(\frac{\pi}{2}\)
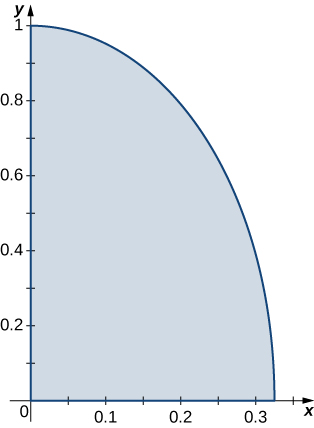
10. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
11. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2, \space y = -x + 2; \space \rho(x,y) = 1\).
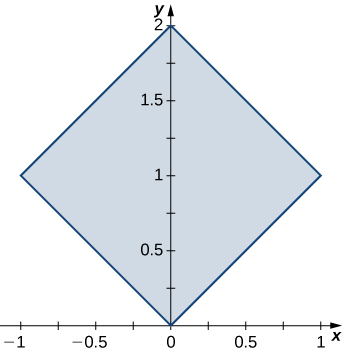
- Answer:
- \(2\)
12. \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
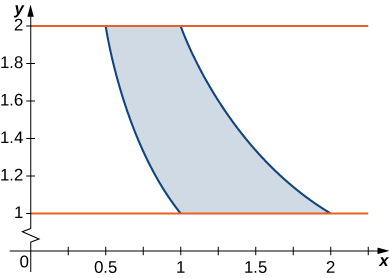
- Answer:
- \(7\)
In exercises 13 - 24, consider a lamina occupying the region \(R\) and having the density function \(\rho\) given in the preceding group of exercises. Use a computer algebra system (CAS) to answer the following questions.
a. Find the moments \(M_x\) and \(M_y\) about the \(x\)-axis and \(y\)-axis, respectively.
b. Calculate and plot the center of mass of the lamina.
c. [T] Use a CAS to locate the center of mass on the graph of \(R\).
13. [T] \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
- Answer:
-
a. \(M_x = \frac{81}{5}, \space M_y = \frac{162}{5}\);
b. \(\bar{x} = \frac{12}{5}, \space \bar{y} = \frac{6}{5}\);
c.
14. [T] \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
15. [T] \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3)\), and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
- Answer:
-
a. \(M_x = \frac{216\sqrt{2}}{5}, \space M_y = \frac{432\sqrt{2}}{5}\);
b. \(\bar{x} = \frac{18}{5}, \space \bar{y} = \frac{9}{5}\);
c.
16. [T] \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).
17. [T] \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and \(x = 0; \space \rho (x,y) = 3xy\).
- Answer:
-
a. \(M_x = \frac{368}{5}, \space M_y = \frac{1552}{5}\);
b. \(\bar{x} = \frac{92}{95}, \space \bar{y} = \frac{388}{95}\);
c.
18. [T] \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x,\) and \(y = -x + 3; \space \rho (x,y) = 2x + y\).
19. [T] \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
- Answer:
-
a. \(M_x = 16\pi, \space M_y = 8\pi\);
b. \(\bar{x} = 1, \space \bar{y} = 2\);
c.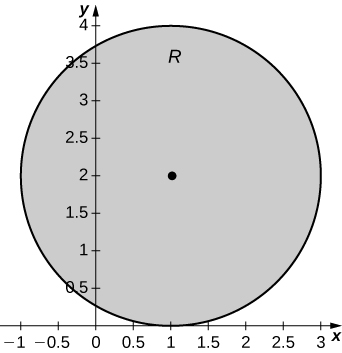
20. [T] \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
21. [T] \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
- Answer:
-
a. \(M_x = 0, \space M_y = 0)\);
b. \(\bar{x} = 0, \space \bar{y} = 0\);
c.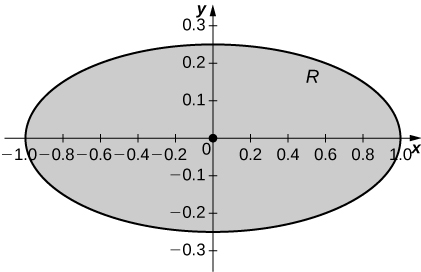
22. [T] \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
23. [T] \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).
- Answer:
-
a. \(M_x = 2, \space M_y = 0)\);
b. \(\bar{x} = 0, \space \bar{y} = 1\);
c.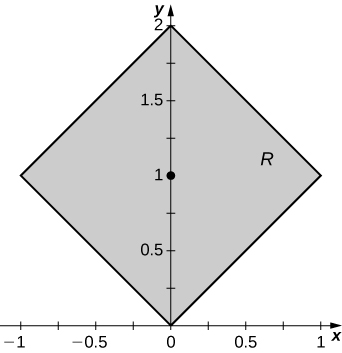
24. [T] \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
In exercises 25 - 36, consider a lamina occupying the region \(R\) and having the density function \(\rho\) given in the first two groups of Exercises.
a. Find the moments of inertia \(I_x, \space I_y\) and \(I_0\) about the \(x\)-axis, \(y\)-axis, and origin, respectively.
b. Find the radii of gyration with respect to the \(x\)-axis, \(y\)-axis, and origin, respectively.
25. \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
- Answer:
- a. \(I_x = \frac{243}{10}, \space I_y = \frac{486}{5}\), and \(I_0 = \frac{243}{2}\);
b. \(R_x = \frac{3\sqrt{5}}{5}, \space R_y = \frac{6\sqrt{5}}{5}\), and \(R_0 = 3\)
26. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
27. \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3)\), and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
- Answer:
- a. \(I_x = \frac{2592\sqrt{2}}{7}, \space I_y = \frac{648\sqrt{2}}{7}\), and \(I_0 = \frac{3240\sqrt{2}}{7}\);
b. \(R_x = \frac{6\sqrt{21}}{7}, \space R_y = \frac{3\sqrt{21}}{7}\), and \(R_0 = \frac{3\sqrt{106}}{7}\)
28. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).
29. \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and x = 0; \space \rho (x,y) = 3xy\).
- Answer:
- a. \(I_x = 88, \space I_y = 1560\), and \(I_0 = 1648\);
b. \(R_x = \frac{\sqrt{418}}{19}, \space R_y = \frac{\sqrt{7410}}{10}\), and \(R_0 = \frac{2\sqrt{1957}}{19}\)
30. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\), and y = -x + 3; \space \rho (x,y) = 2x + y\).
31. \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
- Answer:
- a. \(I_x = \frac{128\pi}{3}, \space I_y = \frac{56\pi}{3}\), and \(I_0 = \frac{184\pi}{3}\);
b. \(R_x = \frac{4\sqrt{3}}{3}, \space R_y = \frac{\sqrt{21}}{2}\), and \(R_0 = \frac{\sqrt{69}}{3}\)
32. \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
33. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
- Answer:
- a. \(I_x = \frac{\pi}{32}, \space I_y = \frac{\pi}{8}\), and \(I_0 = \frac{5\pi}{32}\);
b. \(R_x = \frac{1}{4}, \space R_y = \frac{1}{2}\), and \(R_0 = \frac{\sqrt{5}}{4}\)
34. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
35. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).
- Answer:
- a. \(I_x = \frac{7}{3}, \space I_y = \frac{1}{3}\), and \(I_0 = \frac{8}{3}\);
b. \(R_x = \frac{\sqrt{42}}{6}, \space R_y = \frac{\sqrt{6}}{6}\), and \(R_0 = \frac{2\sqrt{3}}{3}\)
36. \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
37. Let \(Q\) be the solid unit cube. Find the mass of the solid if its density \(\rho\) is equal to the square of the distance of an arbitrary point of \(Q\) to the \(xy\)-plane.
- Answer:
- \(m = \frac{1}{3}\)
38. Let \(Q\) be the solid unit hemisphere. Find the mass of the solid if its density \(\rho\) is proportional to the distance of an arbitrary point of \(Q\) to the origin.
39. The solid \(Q\) of constant density \(1\) is situated inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the sphere \(x^2 + y^2 + z^2 = 1\). Show that the center of mass of the solid is not located within the solid.
40. Find the mass of the solid \(Q = \big\{ (x,y,z) \,|\, 1 \leq x^2 + z^2 \leq 25, \space y \leq 1 - x^2 - z^2 \big\}\) whose density is \(\rho (x,y,z) = k\), where \(k > 0\).
41. The solid \(Q = \big\{ (x,y,z) \,|\, x^2 + y^2 \leq 9, \space 0 \leq z \leq 1, \space x \geq 0, \space y \geq 0\big\}\) has density at each point equal to the distance to the \(xy\)-plane.
a. Find the mass of \(Q\).
b. Find the moments \(M_{xy}, \space M_{xz}\) and \(M_{yz}\) about the \(xy\)-plane, \(xz\)-plane, and \(yz\)-plane, respectively.
c. Find the center of mass of \(Q\).
d. Graph \(Q\) and locate its center of mass.
- Answer:
-
a. \(m = \frac{9\pi}{8}\);
b. \(M_{xy} = \frac{3\pi}{4}, \space M_{xz} = \frac{9}{2}, \space M_{yz} = \frac{9}{2}\);
c. \(\bar{x} = \frac{4}{\pi}, \space \bar{y} = \frac{4}{\pi}, \space \bar{z} = \frac{2}{3}\);
d.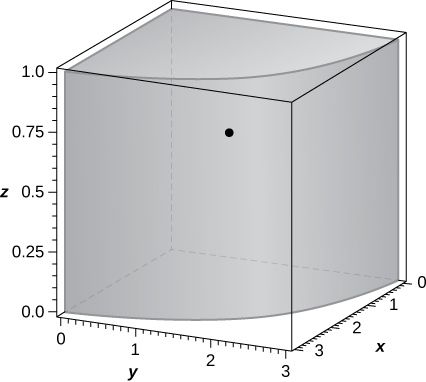
42. Consider the solid \(Q = \big\{ (x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 2, \space 0 \leq z \leq 3\big\}\) with the density function \(\rho(x,y,z) = x + y + 1\).
a. Find the mass of \(Q\).
b. Find the moments \(M_{xy}, \space M_{xz}\) and \(M_{yz}\) about the \(xy\)-plane, \(xz\)-plane, and \(yz\)-plane, respectively.
c. Find the center of mass of \(Q\).
43. [T] The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_{-1}^1 \int_0^{\pi/4} \int_0^1 r^2 \, dr \space d\theta \space dz.\)
Use a CAS to answer the following questions.
- Show that the center of mass of \(Q\) is located in the \(xy\)-plane.
- Graph \(Q\) and locate its center of mass.
- Answer:
-
\(\bar{x} = \frac{3\sqrt{2}}{2\pi}\), \(\bar{y} = \frac{3(2-\sqrt{2})}{2\pi}, \space \bar{z} = 0\); 2. the solid \(Q\) and its center of mass are shown in the following figure.
44. The solid \(Q\) is bounded by the planes \(x + 4y + z = 8, \space x = 0, \space y = 0\), and \(z = 0\). Its density at any point is equal to the distance to the \(xz\)-plane. Find the moments of inertia of the solid about the \(xz\)-plane.
45. The solid \(Q\) is bounded by the planes \(x + y + z = 3, \space x = 0, \space y = 0\), and \(z = 0\). Its density is \(\rho(x,y,z) = x + ay\), where \(a > 0\). Show that the center of mass of the solid is located in the plane \(z = \frac{3}{5}\) for any value of \(a\).
46. Let \(Q\) be the solid situated outside the sphere \(x^2 + y^2 + z^2 = z\) and inside the upper hemisphere \(x^2 + y^2 + z^2 = R^2\), where \(R > 1\). If the density of the solid is \(\rho (x,y,z) = \frac{1}{\sqrt{x^2+y^2+z^2}}\), find \(R\) such that the mass of the solid is \(\frac{7\pi}{2}.\)
47. The mass of a solid \(Q\) is given by \(\displaystyle \int_0^2 \int_0^{\sqrt{4-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^n \, dz \space dy \space dx,\) where \(n\) is an integer. Determine \(n\) such the mass of the solid is \((2 - \sqrt{2}) \pi\).
- Answer:
- \(n = -2\)
48. Let \(Q\) be the solid bounded above the cone \(x^2 + y^2 = z^2\) and below the sphere \(x^2 + y^2 + z^2 - 4z = 0\). Its density is a constant \(k > 0\). Find \(k\) such that the center of mass of the solid is situated \(7\) units from the origin.
49. The solid \(Q = \big\{(x,y,z) \,|\, 0 \leq x^2 + y^2 \leq 16, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x\big\}\) has the density \(\rho (x,y,z) = k\). Show that the moment \(M_{xy}\) about the \(xy\)-plane is half of the moment \(M_{yz}\) about the \(yz\)-plane.
50. The solid \(Q\) is bounded by the cylinder \(x^2 + y^2 = a^2\), the paraboloid \(b^2 - z = x^2 + y^2\), and the \(xy\)-plane, where \(0 < a < b\). Find the mass of the solid if its density is given by \(\rho(x,y,z) = \sqrt{x^2 + y^2}\).
51. Let \(Q\) be a solid of constant density \(k\), where \(k > 0\), that is located in the first octant, inside the circular cone \(x^2 + y^2 = 9(z - 1)^2\), and above the plane \(z = 0\). Show that the moment \(M_{xy}\) about the \(xy\)-plane is the same as the moment \(M_{yz}\) about the \(xz\)-plane.
52. The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_0^1 \int_0^{\pi/2} \int_0^{r^3} (r^4 + r) \space dz \space d\theta \space dr.\)
a. Find the density of the solid in rectangular coordinates.
b. Find the moment \(M_{xy}\) about the \(xy\)-plane.
53. The solid \(Q\) has the moment of inertia \(I_x\) about the \(yz\)-plane given by the triple integral \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}} \int_{\frac{1}{2}(x^2+y^2)}^{\sqrt{x^2+y^2}} (y^2 + z^2)(x^2 + y^2) \, dz \space dx \space dy.\)
a. Find the density of \(Q\).
b. Find the moment of inertia \(I_z\) about the \(xy\)-plane.
- Answer:
- a. \(\rho (x,y,z) = x^2 + y^2\);
b. \(\frac{16\pi}{7}\)
54. The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_0^{\pi/4} \int_0^{2 \space sec \space \theta} \int_0^1 (r^3 \cos \theta \sin \theta + 2r) \, dz \space dr \space d\theta.\)
a. Find the density of the solid in rectangular coordinates.
b. Find the moment \(M_{xz}\) about the \(xz\)-plane.
55. Let \(Q\) be the solid bounded by the \(xy\)-plane, the cylinder \(x^2 + y^2 = a^2\), and the plane \(z = 1\), where \(a > 1\) is a real number. Find the moment \(M_{xy}\) of the solid about the \(xy\)-plane if its density given in cylindrical coordinates is \(\rho(x,y,z) = \frac{d^2f}{dr^2} (r)\), where \(f\) is a differentiable function with the first and second derivatives continuous and differentiable on \((0,a)\).
- Answer:
- \(M_{xy} = \pi (f(0) - f(a) + af'(a))\)
56. A solid \(Q\) has a volume given by \(\displaystyle \iint_D \int_a^b \, dA \space dz\), where \(D\) is the projection of the solid onto the \(xy\)-plane and \(a < b\) are real numbers, and its density does not depend on the variable \(z\). Show that its center of mass lies in the plane \(z = \frac{a+b}{2}\).
57. Consider the solid enclosed by the cylinder \(x^2 + z^2 = a^2\) and the planes \(y = b\) and \(y = c\), where \(a > 0\) and \(b < c\) are real numbers. The density of \(Q\) is given by \(\rho(x,y,z) = f'(y)\), where \(f\) is a differential function whose derivative is continuous on \((b,c)\). Show that if \(f(b) = f(c)\), then the moment of inertia about the \(xz\)-plane of \(Q\) is null.
58. [T] The average density of a solid \(Q\) is defined as \( \displaystyle \rho_{ave} = \frac{1}{V(Q)} \iiint_Q \rho(x,y,z) \, dV = \frac{m}{V(Q)},\) where \(V(Q)\) and \(m\) are the volume and the mass of \(Q\), respectively. If the density of the unit ball centered at the origin is \(\rho (x,y,z) = e^{-x^2-y^2-z^2}\), use a CAS to find its average density. Round your answer to three decimal places.
59. Show that the moments of inertia \(I_x, \space I_y\), and \(I_z\) about the \(yz\)-plane, \(xz\)-plane, and \(xy\)-plane, respectively, of the unit ball centered at the origin whose density is \(\rho (x,y,z) = e^{-x^2-y^2-z^2}\) are the same. Round your answer to two decimal places.
- Answer:
- \(I_x = I_y = I_z \approx 0.84\)
In exercises 1 - 6, the function \(T : S \rightarrow R, \space T (u,v) = (x,y)\) on the region \(S = \big\{(u,v) \,|\, 0 \leq u \leq 1, \space 0 \leq v \leq 1\big\}\) bounded by the unit square is given, where \(R \in R^2\) is the image of \(S\) under \(T\).
a. Justify that the function \(T\) is a \(C^1\) transformation.
b. Find the images of the vertices of the unit square \(S\) through the function \(T\).
c. Determine the image \(R\) of the unit square \(S\) and graph it.
1. \(x = 2u, \space y = 3v\)
2. \(x = \frac{u}{2}, \space y = \frac{v}{3}\)
- Answer:
-
a. \(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = \frac{u}{2}\) and \(y = h(u,v) = \frac{v}{3}\). The functions \(g\) and \(h\) are continuous and differentiable, and the partial derivatives \(g_u (u,v) = \frac{1}{2}, \space g_v (u,v) = 0, \space h_u (u,v) = 0\) and \(h_v (u,v) = \frac{1}{3}\) are continuous on \(S\);
b. \(T(0,0) = (0,0), \space T(1,0) = \left(\frac{1}{2},0\right), \space T(0,1) = \left(0,\frac{1}{3}\right)\), and \(T(1,1) = \left(\frac{1}{2}, \frac{1}{3} \right)\);
c. \(R\) is the rectangle of vertices \((0,0), \space \left(0,\frac{1}{3}\right), \space \left(\frac{1}{2}, \frac{1}{3} \right)\), and \(\left(0,\frac{1}{3}\right)\) in the \(xy\)-plane; the following figure.
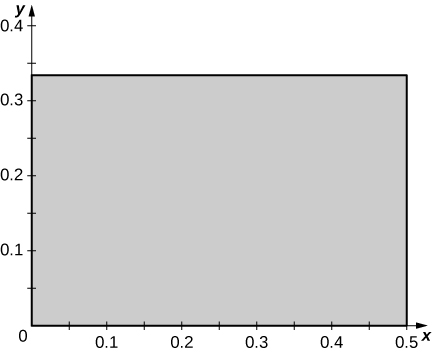
3. \(x = u - v, \space y = u + v\)
4. \(x = 2u - v, \space y = u + 2v\)
- Answer:
-
a. \(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = 2u - v\) and \(y = h(u,v) = u + 2v\). The functions \(g\) and \(h\) are continuous and differentiable, and the partial derivatives \(g_u (u,v) = 2, \space g_v (u,v) = -1, \space h_u (u,v) = 1\) and \(h_v (u,v) = 2\) are continuous on \(S\);
b. \(T(0,0) = (0,0), \space T(1,0) = (2,1), \space T(0,1) = (-1,2)\), and \(T(1,1) = (1,3)\);
c. \(R\) is the parallelogram of vertices \((0,0), \space (2,1) \space (1,3)\), and \((-1,2)\) in the \(xy\)-plane; the following figure.
5. \(x = u^2, \space y = v^2\)
6. \(x = u^3, \space y = v^3\)
- Answer:
-
a. \(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = u^3\) and \(y = h(u,v) = v^3\). The functions \(g\) and \(h\) are continuous and differentiable, and the partial derivatives \(g_u (u,v) = 3u^2, \space g_v (u,v) = 0, \space h_u (u,v) = 0\) and \(h_v (u,v) = 3v^2\) are continuous on \(S\);
b. \(T(0,0) = (0,0), \space T(1,0) = (1,0), \space T(0,1) = (0,1)\), and \(T(1,1) = (1,1)\);
c. \(R\) is the unit square in the \(xy\)-plane see the figure in the answer to the previous exercise.
In exercises 7 - 12, determine whether the transformations \(T : S \rightarrow R\) are one-to-one or not.
7. \(x = u^2, \space y = v^2\), where \(S\) is the rectangle of vertices \((-1,0), \space (1,0), \space (1,1)\), and \((-1,1)\).
8. \(x = u^4, \space y = u^2 + v\), where \(S\) is the triangle of vertices \((-2,0), \space (2,0)\), and \((0,2)\).
- Answer:
- \(T\) is not one-to-one: two points of \(S\) have the same image. Indeed, \(T(-2,0) = T(2,0) = (16,4)\).
9. \(x = 2u, \space y = 3v\), where \(S\) is the square of vertices \((-1,1), \space (-1,-1), \space (1,-1)\), and \((1,1)\).
10. \(T(u, v) = (2u - v, u),\) where \(S\) is the triangle with vertices \((-1,1), \, (-1,-1)\), and \((1,-1)\).
- Answer:
- \(T\) is one-to-one: We argue by contradiction. \(T(u_1,v_1) = T(u_2,v_2)\) implies \(2u_1 - v_1 = 2u_2 - v_2\) and \(u_1 = u_2\). Thus, \(u_1 = u+2\) and \(v_1 = v_2\).
11. \(x = u + v + w, \space y = u + v, \space z = w\), where \(S = R = R^3\).
12. \(x = u^2 + v + w, \space y = u^2 + v, \space z = w\), where \(S = R = R^3\).
- Answer:
- \(T\) is not one-to-one: \(T(1,v,w) = (-1,v,w)\)
In exercises 13 - 18, the transformations \(T : R \rightarrow S\) are one-to-one. Find their related inverse transformations \(T^{-1} : R \rightarrow S\).
13. \(x = 4u, \space y = 5v\), where \(S = R = R^2\).
14. \(x = u + 2v, \space y = -u + v\), where \(S = R = R^2\).
- Answer:
- \(u = \frac{x-2y}{3}, \space v= \frac{x+y}{3}\)
15. \(x = e^{2u+v}, \space y = e^{u-v}\), where \(S = R^2\) and \(R = \big\{(x,y) \,|\, x > 0, \space y > 0\big\}\)
16. \(x = \ln u, \space y = \ln(uv)\), where \(S = \big\{(u,v) \,|\, u > 0, \space v > 0\big\}\) and \(R = R^2\).
- Answer:
- \(u = e^x, \space v = e^{-x+y}\)
17. \(x = u + v + w, \space y = 3v, \space z = 2w\), where \(S = R = R^3\).
18. \(x = u + v, \space y = v + w, \space z = u + w\), where \(S = R = R^3\).
- Answer:
- \(u = \frac{x-y+z}{2}, \space v = \frac{x+y-z}{2}, \space w = \frac{-x+y+z}{2}\)
In exercises 19 - 22, the transformation \(T : S \rightarrow R, \space T (u,v) = (x,y)\) and the region \(R \subset R^2\) are given. Find the region \(S \subset R^2\).
19. \(x = au, \space y = bv, \space R = \big\{(x,y) \,|\, x^2 + y^2 \leq a^2 b^2\big\}\) where \(a,b > 0\)
20. \(x = au, \space y = bc, \space R = \big\{(x,y) \,|\, \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1\big\}\), where \(a,b > 0\)
- Answer:
- \(S = \big\{(u,v) \,|\, u^2 + v^2 \leq 1\big\}\)
21. \(x = \frac{u}{a}, \space y = \frac{v}{b}, \space z = \frac{w}{c}, \space R = \big\{(x,y)\,|\,x^2 + y^2 + z^2 \leq 1\big\}\), where \(a,b,c > 0\)
22. \(x = au, \space y = bv, \space z = cw, \space R = \big\{(x,y)\,|\,\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \leq 1, \space z > 0\big\}\), where \(a,b,c > 0\)
- Answer:
- \(R = \big\{(u,v,w)\,|\,u^2 - v^2 - w^2 \leq 1, \space w > 0\big\}\)
In exercises 23 - 32, find the Jacobian \(J\) of the transformation.
23. \(x = u + 2v, \space y = -u + v\)
24. \(x = \frac{u^3}{2}, \space y = \frac{v}{u^2}\)
- Answer:
- \(\frac{3}{2}\)
25. \(x = e^{2u-v}, \space y = e^{u+v}\)
26. \(x = ue^v, \space y = e^{-v}\)
- Answer:
- \(-1\)
27. \(x = u \space \cos (e^v), \space y = u \space \sin(e^v)\)
28. \(x = v \space \sin (u^2), \space y = v \space \cos(u^2)\)
- Answer:
- \(2uv\)
29. \(x = u \space \cosh v, \space y = u \space \sinh v, \space z = w\)
30. \(x = v \space \cosh \left(\frac{1}{u}\right), \space y = v \space \sinh \left(\frac{1}{u}\right), \space z = u + w^2\)
- Answer:
- \(\frac{v}{u^2}\)
31. \(x = u + v, \space y = v + w, \space z = u\)
32. \(x = u - v, \space y = u + v, \space z = u + v + w\)
- Answer:
- \(2\)
33. The triangular region \(R\) with the vertices \((0,0), \space (1,1)\), and \((1,2)\) is shown in the following figure.
a. Find a transformation \(T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)\), where \(a,b,c\), and \(d\) are real numbers with \(ad - bc \neq 0\) such that \(T^{-1} (0,0) = (0,0), \space T^{-1} (1,1) = (1,0)\), and \(T^{-1}(1,2) = (0,1)\).
b. Use the transformation \(T\) to find the area \(A(R)\) of the region \(R\).
34. The triangular region \(R\) with the vertices \((0,0), \space (2,0)\), and \((1,3)\) is shown in the following figure.
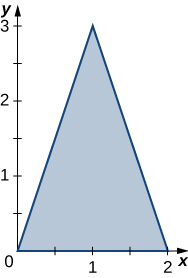
a. Find a transformation \(T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)\), where \(a,b,c\), and \(d\) are real numbers with \(ad - bc \neq 0\) such that \(T^{-1} (0,0) = (0,0), \space T^{-1} (2,0) = (1,0)\), and \(T^{-1}(1,3) = (0,1)\).
b. Use the transformation \(T\) to find the area \(A(R)\) of the region \(R\).
- Answer:
-
a. \(T (u,v) = (2u + v, \space 3v)\)
b. The area of \(R\) is \(\displaystyle A(R) = \int_0^3 \int_{y/3}^{(6-y)/3} \, dx \, dy = \int_0^1 \int_0^{1-u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \, dv \space du = \int_0^1 \int_0^{1-u} 6 \, dv \, du = 3.\)
In exercises 35 - 36, use the transformation \(u = y - x, \space v = y\), to evaluate the integrals on the parallelogram \(R\) of vertices \((0,0), \space (1,0), \space (2,1)\), and \((1,1)\) shown in the following figure.
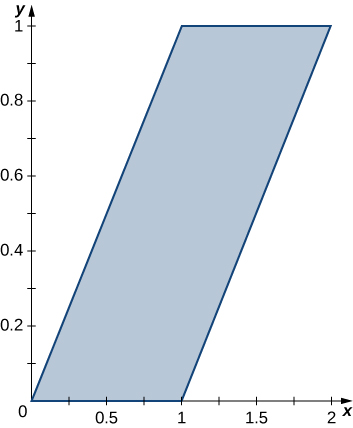
35. \(\displaystyle \iint_R (y - x) \, dA\)
36. \(\displaystyle \iint_R (y^2 - xy) \, dA\)
- Answer:
- \(-\frac{1}{4}\)
In exercises 37 - 38, use a change of variables to evaluate the double integrals over the given region R. Graph the region.
37. \(\displaystyle \iint_R e^{xy} \, dA \) where \(R\) is bounded by \(y=4x, \space y=x, \space y=4/x \space and \space y=1/x\)
- Answer:
- \((e^4-e)\ln 2\)
38. \(\displaystyle \iint_R \sin (x - y) \, dA\) where \(R\) is the square with the vertices \((0,0), \space (1,1)\), \((2,0), \space and (1,-1)\)
- Answer:
- \(1-\cos 2\)
In exercises 39 - 40, use the transformation \(x = u, \space 5y = v\) to evaluate the integrals on the region \(R\) bounded by the ellipse \(x^2 + 25y^2 = 1\) shown in the following figure.
39. \(\displaystyle \iint_R \sqrt{x^2 + 25y^2} \, dA\)
40. \(\displaystyle \iint_R (x^2 + 25y^2)^2 \, dA\)
- Answer:
- \(\frac{\pi}{15}\)
In exercises 41 - 42, use the transformation \(u = x + y, \space v = x - y\) to evaluate the integrals on the trapezoidal region \(R\) determined by the points \((1,0), \space (2,0), \space (0,2)\), and \((0,1)\) shown in the following figure.
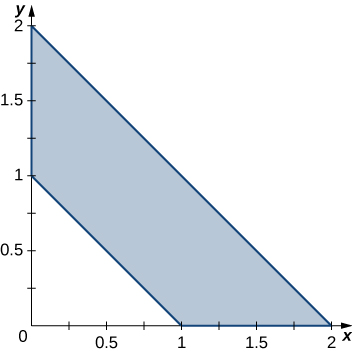
41. \(\displaystyle \iint_R (x^2 - 2xy + y^2) \space e^{x+y} \, dA\)
42. \(\displaystyle \iint_R (x^3 + 3x^2y + 3xy^2 + y^3) \, dA\)
- Answer:
- \(\frac{31}{5}\)
43. The circular annulus sector \(R\) bounded by the circles \(4x^2 + 4y^2 = 1\) and \(9x^2 + 9y^2 = 64\), the line \(x = y \sqrt{3}\), and the \(y\)-axis is shown in the following figure. Find a transformation \(T\) from a rectangular region \(S\) in the \(r\theta\)-plane to the region \(R\) in the \(xy\)-plane. Graph \(S\).
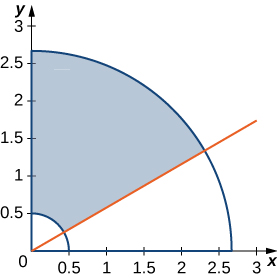
44. The solid \(R\) bounded by the circular cylinder \(x^2 + y^2 = 9\) and the planes \(z = 0, \space z = 1, \space x = 0\), and \(y = 0\) is shown in the following figure. Find a transformation \(T\) from a cylindrical box \(S\) in \(r\theta z\)-space to the solid \(R\) in \(xyz\)-space.
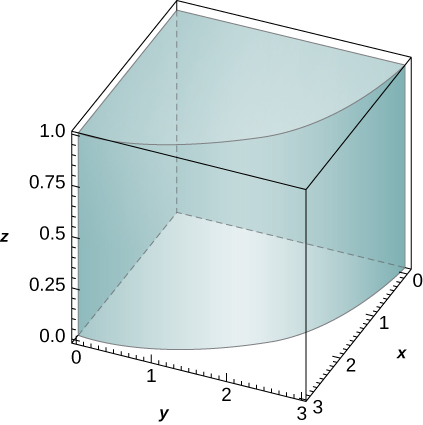
- Answer:
- \(T (r,\theta,z) = (r \space \cos \theta, \space r \space \sin \theta, \space z); \space S = [0,3] \times [0,\frac{\pi}{2}] \times [0,1]\) in the \(r\theta z\)-space
45. Show that \[\iint_R f \left(\sqrt{\frac{x^2}{3} + \frac{y^2}{3}}\right) dA = 2 \pi \sqrt{15} \int_0^1 f (\rho) \rho \space d\rho,\] where \(f\) is a continuous function on \([0,1]\) and \(R\) is the region bounded by the ellipse \(5x^2 + 3y^2 = 15\).
46. Show that \[\iiint_R f \left(\sqrt{16x^2 + 4y^2 + z^2}\right) dV = \frac{\pi}{2} \int_0^1 f (\rho) \rho^2 d\rho,\] where \(f\) is a continuous function on \([0,1]\) and \(R\) is the region bounded by the ellipsoid \(16x^2 + 4y^2 + z^2 = 1\).
47. [T] Find the area of the region bounded by the curves \(xy = 1, \space xy = 3, \space y = 2x\), and \(y = 3x\) by using the transformation \(u = xy\) and \(v = \frac{y}{x}\). Use a computer algebra system (CAS) to graph the boundary curves of the region \(R\).
48. [T] Find the area of the region bounded by the curves \(x^2y = 2, \space x^2y = 3, \space y = x\), and \(y = 2x\) by using the transformation \(u = x^2y\) and \(v = \frac{y}{x}\). Use a CAS to graph the boundary curves of the region \(R\).
- Answer:
-
The area of \(R\) is \(10 - 4\sqrt{6}\); the boundary curves of \(R\) are graphed in the following figure.
49. Evaluate the triple integral \[\int_0^1 \int_1^2 \int_z^{z+1} (y + 1) \space dx \space dy \space dz\] by using the transformation \(u = x - z, \space v = 3y\), and \(w = \frac{z}{2}\).
50. Evaluate the triple integral \[\int_0^2 \int_4^6 \int_{3z}^{3z+2} (5 - 4y) \space dx \space dy \space dz\] by using the transformation \(u = x - 3z, \space v = 4y\), and \(w = z\).
- Answer:
- \(8\)
51. A transformation \(T : R^2 \rightarrow R^2, \space T (u,v) = (x,y)\) of the form \(x = au + bv, \space y = cu + dv\), where \(a,b,c\), and \(d\) are real numbers, is called linear. Show that a linear transformation for which \(ad - bc \neq 0\) maps parallelograms to parallelograms.
52. A transformation \(T_{\theta} : R^2 \rightarrow R^2, \space T_{\theta} (u,v) = (x,y)\) of the form \(x = u \space \cos \theta - v \space \sin \theta, \space y = u \space \sin \theta + v \space \cos \theta\), is called a rotation angle \(\theta\). Show that the inverse transformation of \(T_{\theta}\) satisfies \(T_{\theta}^{-1} = T_{-\theta}\) where \(T_{-\theta}\) is the rotation of angle \(-\theta\).
53. [T] Find the region \(S\) in the \(uv\)-plane whose image through a rotation of angle \(\frac{\pi}{4}\) is the region \(R\) enclosed by the ellipse \(x^2 + 4y^2 = 1\). Use a CAS to answer the following questions.
a. Graph the region \(S\).
b. Evaluate the integral \(\displaystyle \iint_S e^{-2uv} \, du \, dv.\) Round your answer to two decimal places.
54. [T] The transformations \(T_i : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space i = 1, . . . , 4,\) defined by \(T_1(u,v) = (u,-v), \space T_2 (u,v) = (-u,v), \space T_3 (u,v) = (-u, -v)\), and \(T_4 (u,v) = (v,u)\) are called reflections about the \(x\)-axis, \(y\)-axis origin, and the line \(y = x\), respectively.
a. Find the image of the region \(S = \big\{(u,v)\,|\,u^2 + v^2 - 2u - 4v + 1 \leq 0\big\}\) in the \(xy\)-plane through the transformation \(T_1 \circ T_2 \circ T_3 \circ T_4\).
b. Use a CAS to graph \(R\).
c. Evaluate the integral \(\displaystyle \iint_S \sin (u^2) \, du \, dv\) by using a CAS. Round your answer to two decimal places.
- Answer:
-
a. \(R = \big\{(x,y)\,|\,y^2 + x^2 - 2y - 4x + 1 \leq 0\big\}\);
b. \(R\) is graphed in the following figure;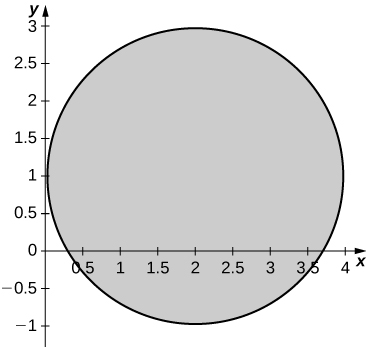
c. \(3.16\)
55. [T] The transformations \(T_{k,1,1} : \mathbb{R}^3 \rightarrow \mathbb{R}^3, \space T_{k,1,1}(u,v,w) = (x,y,z)\) of the form \(x = ku, \space y = v, \space z = w\), where \(k \neq 1\) is a positive real number, is called a stretch if \(k > 1\) and a compression if \(0 < k < 1\) in the \(x\)-direction. Use a CAS to evaluate the integral \(\displaystyle \iiint_S e^{-(4x^2+9y^2+25z^2)} \, dx \, dy \, dz\) on the solid \(S = \big\{(x,y,z) \,|\, 4x^2 + 9y^2 + 25z^2 \leq 1\big\}\) by considering the compression \(T_{2,3,5}(u,v,w) = (x,y,z)\) defined by \(x = \frac{u}{2}, \space y = \frac{v}{3}\), and \(z = \frac{w}{5}\). Round your answer to four decimal places.
56. [T] The transformation \(T_{a,0} : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space T_{a,0} (u,v) = (u + av, v)\), where \(a \neq 0\) is a real number, is called a shear in the \(x\)-direction. The transformation, \(T_{b,0} : R^2 \rightarrow R^2, \space T_{o,b}(u,v) = (u,bu + v)\), where \(b \neq 0\) is a real number, is called a shear in the \(y\)-direction.
a. Find transformations \(T_{0,2} \circ T_{3,0}\).
b. Find the image \(R\) of the trapezoidal region \(S\) bounded by \(u = 0, \space v = 0, \space v = 1\), and \(v = 2 - u\) through the transformation \(T_{0,2} \circ T_{3,0}\).
c. Use a CAS to graph the image \(R\) in the \(xy\)-plane.
d. Find the area of the region \(R\) by using the area of region \(S\).
- Answer:
-
a. \(T_{0,2} \circ T_{3,0}(u,v) = (u + 3v, 2u + 7v)\);
b. The image \(S\) is the quadrilateral of vertices \((0,0), \space (3,7), \space (2,4)\), and \((4,9)\);
c. \(S\) is graphed in the following figure;
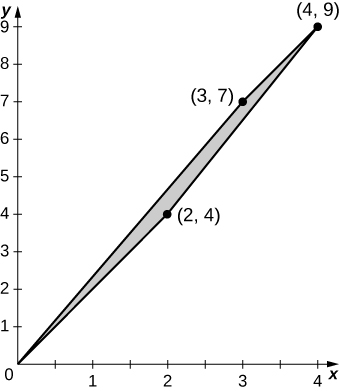
d. \(\frac{3}{2}\)
57. Use the transformation, \(x = au, \space y = av, \space z = cw\) and spherical coordinates to show that the volume of a region bounded by the spheroid \(\frac{x^2+y^2}{a^2} + \frac{z^2}{c^2} = 1\) is \(\frac{4\pi a^2c}{3}\).
58. Find the volume of a football whose shape is a spheroid \(\frac{x^2+y^2}{a^2} + \frac{z^2}{c^2} = 1\) whose length from tip to tip is \(11\) inches and circumference at the center is \(22\) inches. Round your answer to two decimal places.
- Answer:
- \(\frac{2662}{3\pi} \approx 282.45 \space in^3\)