5.2: Vector Fields
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Recognize a vector field in a plane or in space.
- Sketch a vector field from a given equation.
- Identify a conservative field and its associated potential function.
- Explain how to find a potential function for a conservative vector field.
- Explain how to test a vector field to determine whether it is conservative.
Vector fields are an important tool for describing many physical concepts, such as gravitation and electromagnetism, which affect the behavior of objects over a large region of a plane or of space. They are also useful for dealing with large-scale behavior such as atmospheric storms or deep-sea ocean currents. In this section, we examine the basic definitions and graphs of vector fields so we can study them in more detail in the rest of this chapter.
Examples of Vector Fields
How can we model the gravitational force exerted by multiple astronomical objects? How can we model the velocity of water particles on the surface of a river? Figure 5.2.1 gives visual representations of such phenomena.
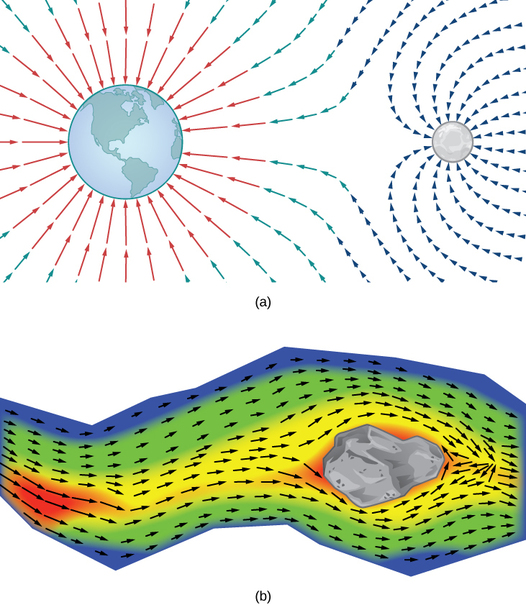
Figure 5.2.1a shows a gravitational field exerted by two astronomical objects, such as a star and a planet or a planet and a moon. At any point in the figure, the vector associated with a point gives the net gravitational force exerted by the two objects on an object of unit mass. The vectors of largest magnitude in the figure are the vectors closest to the larger object. The larger object has greater mass, so it exerts a gravitational force of greater magnitude than the smaller object.
Figure 5.2.1b shows the velocity of a river at points on its surface. The vector associated with a given point on the river’s surface gives the velocity of the water at that point. Since the vectors to the left of the figure are small in magnitude, the water is flowing slowly on that part of the surface. As the water moves from left to right, it encounters some rapids around a rock. The speed of the water increases, and a whirlpool occurs in part of the rapids.
Each figure illustrates an example of a vector field. Intuitively, a vector field is a map of vectors. In this section, we study vector fields in ℝ2 and ℝ3.
DEFINITION: vector field
- A vector field ⇀F in ℝ2 is an assignment of a two-dimensional vector ⇀F(x,y) to each point (x,y) of a subset D of ℝ2. The subset D is the domain of the vector field.
- A vector field ⇀F in ℝ3 is an assignment of a three-dimensional vector ⇀F(x,y,z) to each point (x,y,z) of a subset D of ℝ3. The subset D is the domain of the vector field.
Vector Fields in ℝ2
A vector field in ℝ2 can be represented in either of two equivalent ways. The first way is to use a vector with components that are two-variable functions:
⇀F(x,y)=⟨P(x,y),Q(x,y)⟩
The second way is to use the standard unit vectors:
⇀F(x,y)=P(x,y)ˆi+Q(x,y)ˆj.
A vector field is said to be continuous if its component functions are continuous.
Example 5.2.1: Finding a Vector Associated with a Given Point
Let ⇀F(x,y)=(2y2+x−4)ˆi+cos(x)ˆj be a vector field in ℝ2. Note that this is an example of a continuous vector field since both component functions are continuous. What vector is associated with point (0,−1)?
Solution
Substitute the point values for x and y:
⇀F(0,−1)=(2(−1)2+0−4)ˆi+cos(0)ˆj=−2ˆi+ˆj.
Exercise 5.2.1
Let ⇀G(x,y)=x2yˆi−(x+y)ˆj be a vector field in ℝ2. What vector is associated with the point (−2,3)?
- Hint
-
Substitute the point values into the vector function.
- Answer
-
⇀G(−2,3)=12ˆi−ˆj
Drawing a Vector Field
We can now represent a vector field in terms of its components of functions or unit vectors, but representing it visually by sketching it is more complex because the domain of a vector field is in ℝ2, as is the range. Therefore the “graph” of a vector field in ℝ2 lives in four-dimensional space. Since we cannot represent four-dimensional space visually, we instead draw vector fields in ℝ2 in a plane itself. To do this, draw the vector associated with a given point at the point in a plane. For example, suppose the vector associated with point (4,−1) is ⟨3,1⟩. Then, we would draw vector ⟨3,1⟩ at point (4,−1).
We should plot enough vectors to see the general shape, but not so many that the sketch becomes a jumbled mess. If we were to plot the image vector at each point in the region, it would fill the region completely and is useless. Instead, we can choose points at the intersections of grid lines and plot a sample of several vectors from each quadrant of a rectangular coordinate system in ℝ2.
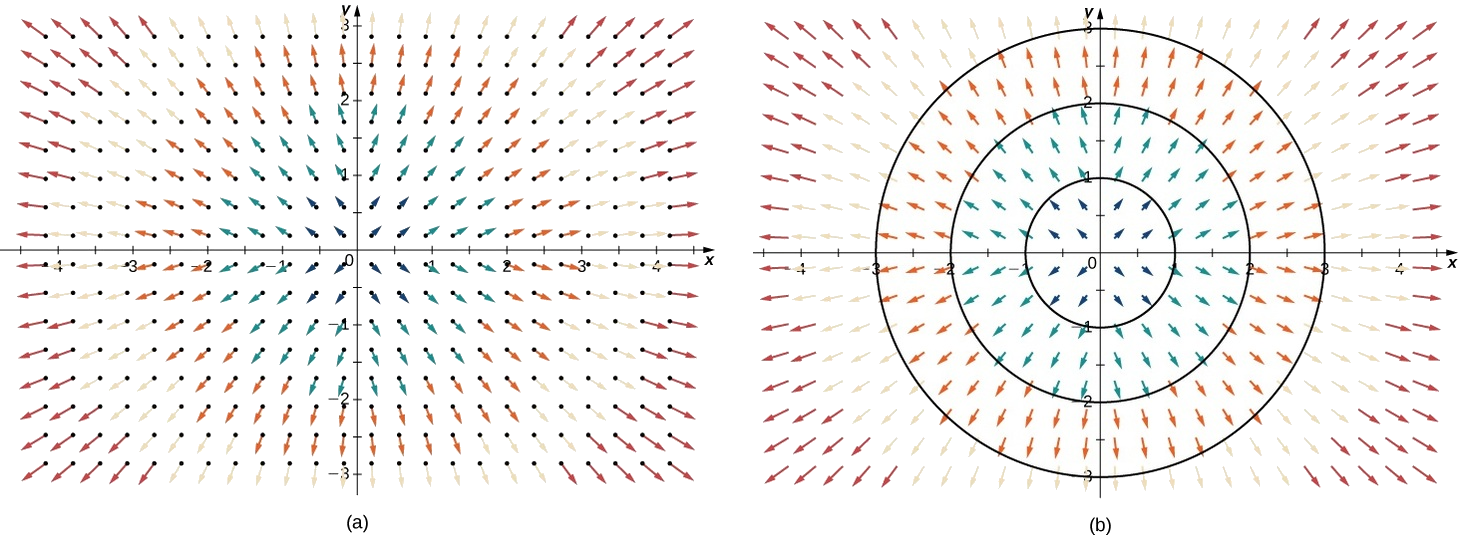
There are two types of vector fields in ℝ2 on which this chapter focuses: radial fields and rotational fields. Radial fields model certain gravitational fields and energy source fields, and rotational fields model the movement of a fluid in a vortex. In a radial field, all vectors either point directly toward or directly away from the origin. Furthermore, the magnitude of any vector depends only on its distance from the origin. In a radial field, the vector located at point (x,y) is perpendicular to the circle centered at the origin that contains point (x,y), and all other vectors on this circle have the same magnitude.
Example 5.2.2: Drawing a Radial Vector Field
Sketch the vector field ⇀F(x,y)=x2ˆi+y2ˆj.
Solution
To sketch this vector field, choose a sample of points from each quadrant and compute the corresponding vector. The following table gives a representative sample of points in a plane and the corresponding vectors.
| (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) |
|---|---|---|---|---|---|
| (1,0) | ⟨12,0⟩ | (2,0) | ⟨1,0⟩ | (1,1) | ⟨12,12⟩ |
| (0,1) | ⟨0,12⟩ | (0,2) | ⟨0,1⟩ | (−1,1) | ⟨−12,12⟩ |
| (−1,0) | ⟨−12,0⟩ | (−2,0) | ⟨−1,0⟩ | (−1,−1) | ⟨−12,−12⟩ |
| (0,−1) | ⟨0,−12⟩ | (0,−2) | ⟨0,−1⟩ | (1,−1) | ⟨12,−12⟩ |
Figure 5.2.2a shows the vector field. To see that each vector is perpendicular to the corresponding circle, Figure 5.2.2b shows circles overlain on the vector field.
Exercise 5.2.2
Draw the radial field ⇀F(x,y)=−x3ˆi−y3ˆj.
- Hint
-
Sketch enough vectors to get an idea of the shape.
- Answer
-

In contrast to radial fields, in a rotational field, the vector at point (x,y) is tangent (not perpendicular) to a circle with radius r=√x2+y2. In a standard rotational field, all vectors point either in a clockwise direction or in a counterclockwise direction, and the magnitude of a vector depends only on its distance from the origin. Both of the following examples are clockwise rotational fields, and we see from their visual representations that the vectors appear to rotate around the origin.
Example 5.2.3: Drawing a Rotational Vector Field
Sketch the vector field ⇀F(x,y)=⟨y,−x⟩.
Solution
Create a table (see the one that follows) using a representative sample of points in a plane and their corresponding vectors. Figure 5.2.3 shows the resulting vector field.
| (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) |
|---|---|---|---|---|---|
| (1,0) | ⟨0,−1⟩ | (2,0) | ⟨0,−2⟩ | (1,1) | ⟨1,−1⟩ |
| (0,1) | ⟨1,0⟩ | (0,2) | ⟨2,0⟩ | (−1,1) | ⟨1,1⟩ |
| (−1,0) | ⟨0,1⟩ | (−2,0) | ⟨0,2⟩ | (−1,−1) | ⟨−1,1⟩ |
| (0,−1) | ⟨−1,0⟩ | (0,−2) | ⟨−2,0⟩ | (1,−1) | ⟨−1,−1⟩ |
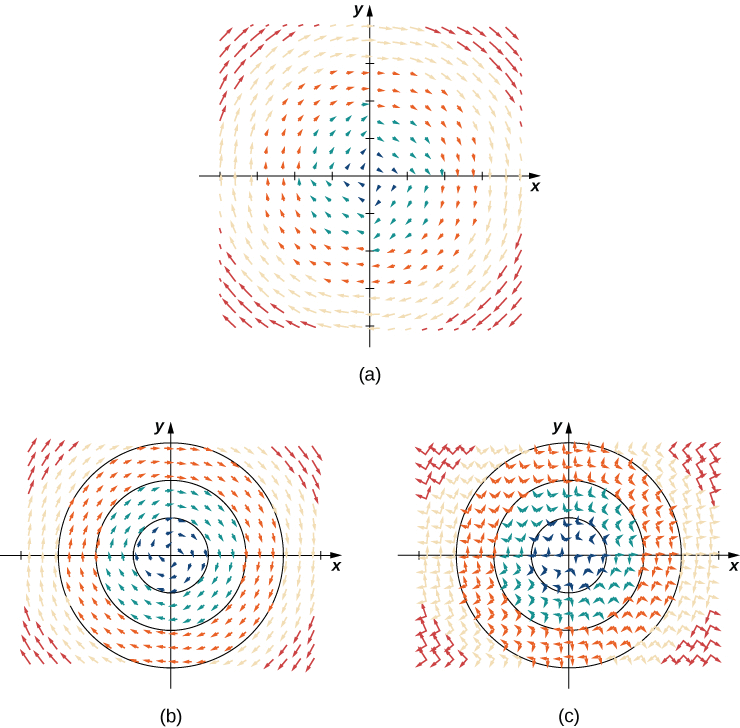
Analysis
Note that vector ⇀F(a,b)=⟨b,−a⟩ points clockwise and is perpendicular to radial vector ⟨a,b⟩. (We can verify this assertion by computing the dot product of the two vectors: ⟨a,b⟩·⟨−b,a⟩=−ab+ab=0.) Furthermore, vector ⟨b,−a⟩ has length r=√a2+b2. Thus, we have a complete description of this rotational vector field: the vector associated with point (a,b) is the vector with length r tangent to the circle with radius r, and it points in the clockwise direction.
Sketches such as that in Figure 5.2.3 are often used to analyze major storm systems, including hurricanes and cyclones. In the northern hemisphere, storms rotate counterclockwise; in the southern hemisphere, storms rotate clockwise. (This is an effect caused by Earth’s rotation about its axis and is called the Coriolis Effect.)

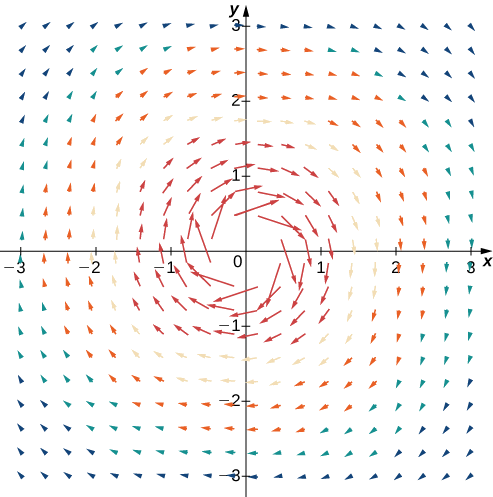
Example 5.2.4: Sketching a Vector Field
Sketch vector field ⇀F(x,y)=yx2+y2ˆi,−xx2+y2ˆj.
Solution
To visualize this vector field, first note that the dot product ⇀F(a,b)·(aˆi+bˆj) is zero for any point (a,b). Therefore, each vector is tangent to the circle on which it is located. Also, as (a,b)→(0,0), the magnitude of ⇀F(a,b) goes to infinity. To see this, note that
||⇀F(a,b)||=√a2+b2(a2+b2)2=√1a2+b2.
Since 1a2+b2→∞ as (a,b)→(0,0), then ||⇀F(a,b)||→∞ as (a,b)→(0,0). This vector field looks similar to the vector field in Example 5.2.3, but in this case the magnitudes of the vectors close to the origin are large. Table 5.2.3 shows a sample of points and the corresponding vectors, and Figure 5.2.5 shows the vector field. Note that this vector field models the whirlpool motion of the river in Figure 5.2.5(b). The domain of this vector field is all of ℝ2 except for point (0,0).
| (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) | (x,y) | ⇀F(x,y) |
|---|---|---|---|---|---|
| (1,0) | ⟨0,−1⟩ | (2,0) | ⟨0,−12⟩ | (1,1) | ⟨12,−12⟩ |
| (0,1) | ⟨1,0⟩ | (0,2) | ⟨12,0⟩ | (−1,1) | ⟨12,12⟩ |
| (−1,0) | ⟨0,1⟩ | (−2,0) | ⟨0,12⟩ | (−1,−1) | ⟨−12,12⟩ |
| (0,−1) | ⟨−1,0⟩ | (0,−2) | ⟨−12,0⟩ | (1,−1) | ⟨−12,−12⟩ |
Exercise 5.2.4
Sketch vector field ⇀F(x,y)=⟨−2y,2x⟩. Is the vector field radial, rotational, or neither?
- Hint
-
Substitute enough points into ⇀F to get an idea of the shape.
- Answer
-
Rotational

Example 5.2.5: Velocity Field of a Fluid
Suppose that ⇀v(x,y)=−2yx2+y2ˆi+2xx2+y2ˆj is the velocity field of a fluid. How fast is the fluid moving at point (1,−1)? (Assume the units of speed are meters per second.)
Solution
To find the velocity of the fluid at point (1,−1), substitute the point into ⇀v:
⇀v(1,−1)=−2(−1)1+1ˆi+2(1)1+1ˆj=ˆi+ˆj.
The speed of the fluid at (1,−1) is the magnitude of this vector. Therefore, the speed is ||ˆi+ˆj||=√2 m/sec.
Exercise 5.2.5
Vector field ⇀v(x,y)=⟨4|x|,1⟩ models the velocity of water on the surface of a river. What is the speed of the water at point (2,3)? Use meters per second as the units.
- Hint
-
Remember, speed is the magnitude of velocity.
- Answer
-
√65 m/sec
We have examined vector fields that contain vectors of various magnitudes, but just as we have unit vectors, we can also have a unit vector field. A vector field ⇀F is a unit vector field if the magnitude of each vector in the field is 1. In a unit vector field, the only relevant information is the direction of each vector.
Example 5.2.6: A Unit Vector Field
Show that vector field ⇀F(x,y)=⟨y√x2+y2,−x√x2+y2⟩ is a unit vector field.
Solution
To show that ⇀F is a unit field, we must show that the magnitude of each vector is 1. Note that
√(y√x2+y2)2+(−x√x2+y2)2=√y2x2+y2+x2x2+y2=√x2+y2x2+y2=1
Therefore, ⇀F is a unit vector field.
Exercise 5.2.6
Is vector field ⇀F(x,y)=⟨−y,x⟩ a unit vector field?
- Hint
-
Calculate the magnitude of ⇀F at an arbitrary point (x,y).
- Answer
-
No.
Why are unit vector fields important? Suppose we are studying the flow of a fluid, and we care only about the direction in which the fluid is flowing at a given point. In this case, the speed of the fluid (which is the magnitude of the corresponding velocity vector) is irrelevant, because all we care about is the direction of each vector. Therefore, the unit vector field associated with velocity is the field we would study.
If ⇀F=⟨P,Q,R⟩ is a vector field, then the corresponding unit vector field is ⟨P||⇀F||,Q||⇀F||,R||⇀F||⟩. Notice that if ⇀F(x,y)=⟨y,−x⟩ is the vector field from Example 5.2.6, then the magnitude of ⇀F is √x2+y2, and therefore the corresponding unit vector field is the field ⇀G from the previous example.
If ⇀F is a vector field, then the process of dividing ⇀F by its magnitude to form unit vector field ⇀F/||⇀F|| is called normalizing the field ⇀F.
Vector Fields in ℝ3
We have seen several examples of vector fields in ℝ2; let’s now turn our attention to vector fields in ℝ3. These vector fields can be used to model gravitational or electromagnetic fields, and they can also be used to model fluid flow or heat flow in three dimensions. A two-dimensional vector field can really only model the movement of water on a two-dimensional slice of a river (such as the river’s surface). Since a river flows through three spatial dimensions, to model the flow of the entire depth of the river, we need a vector field in three dimensions.
The extra dimension of a three-dimensional field can make vector fields in ℝ3 more difficult to visualize, but the idea is the same. To visualize a vector field in ℝ3, plot enough vectors to show the overall shape. We can use a similar method to visualizing a vector field in ℝ2 by choosing points in each octant.
Just as with vector fields in ℝ2, we can represent vector fields in ℝ3 with component functions. We simply need an extra component function for the extra dimension. We write either
⇀F(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩
or
⇀F(x,y,z)=P(x,y,z)ˆi+Q(x,y,z)ˆj+R(x,y,z)ˆk.
Example 5.2.7: Sketching a Vector Field in Three Dimensions
Describe vector field ⇀F(x,y,z)=⟨1,1,z⟩.
Solution
For this vector field, the x- and y-components are constant, so every point in ℝ3 has an associated vector with x- and y-components equal to one. To visualize ⇀F, we first consider what the field looks like in the xy-plane. In the xy-plane, z=0. Hence, each point of the form (a,b,0) has vector ⟨1,1,0⟩ associated with it. For points not in the xy-plane but slightly above it, the associated vector has a small but positive z-component, and therefore the associated vector points slightly upward. For points that are far above the xy-plane, the z-component is large, so the vector is almost vertical. Figure 5.2.6 shows this vector field.
Figure 5.2.6: A visual representation of vector field ⇀F(x,y,z)=⟨1,1,z⟩.
Exercise 5.2.7
Sketch vector field ⇀G(x,y,z)=⟨2,z2,1⟩.
- Hint
-
Substitute enough points into the vector field to get an idea of the general shape.
- Answer
In the next example, we explore one of the classic cases of a three-dimensional vector field: a gravitational field.
Example 5.2.8: Describing a Gravitational Vector Field
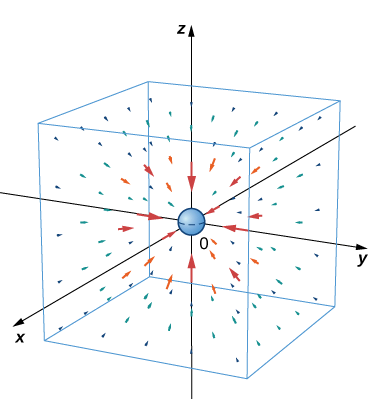
Newton’s law of gravitation states that ⇀F=−Gm1m2r2ˆr, where G is the universal gravitational constant. It describes the gravitational field exerted by an object (object 1) of mass m1 located at the origin on another object (object 2) of mass m2 located at point (x,y,z). Field ⇀F denotes the gravitational force that object 1 exerts on object 2, r is the distance between the two objects, and ˆr indicates the unit vector from the first object to the second. The minus sign shows that the gravitational force attracts toward the origin; that is, the force of object 1 is attractive. Sketch the vector field associated with this equation.
Solution
Since object 1 is located at the origin, the distance between the objects is given by r=√x2+y2+z2. The unit vector from object 1 to object 2 is ˆr=⟨x,y,z⟩||⟨x,y,z⟩||, and hence ˆr=⟨xr,yr,zr⟩. Therefore, gravitational vector field ⇀F exerted by object 1 on object 2 is
⇀F=−Gm1m2⟨xr3,yr3,zr3⟩.
This is an example of a radial vector field in ℝ3.
Figure 5.2.7 shows what this gravitational field looks like for a large mass at the origin. Note that the magnitudes of the vectors increase as the vectors get closer to the origin.
Exercise 5.2.8
The mass of asteroid 1 is 750,000 kg and the mass of asteroid 2 is 130,000 kg. Assume asteroid 1 is located at the origin, and asteroid 2 is located at (15,−5,10), measured in units of 10 to the eighth power kilometers. Given that the universal gravitational constant is G=6.67384×10−11m3kg−1s−2, find the gravitational force vector that asteroid 1 exerts on asteroid 2.
- Hint
-
Follow Example 5.2.8 and first compute the distance between the asteroids.
- Answer
-
1.49063×10−18, 4.96876×10−19, 9.93752×10−19 N
Gradient Fields (Conservative Fields)
In this section, we study a special kind of vector field called a gradient field or a conservative field. These vector fields are extremely important in physics because they can be used to model physical systems in which energy is conserved. Gravitational fields and electric fields associated with a static charge are examples of gradient fields.
Recall that if f is a (scalar) function of x and y, then the gradient of f is
gradf=⇀∇f(x,y)=fx(x,y)ˆi+fy(x,y)ˆj.
We can see from the form in which the gradient is written that ⇀∇f is a vector field in ℝ2. Similarly, if f is a function of x, y, and z, then the gradient of f is
gradf=⇀∇f(x,y,z)=fx(x,y,z)ˆi+fy(x,y,z)ˆj+fz(x,y,z)ˆk.
The gradient of a three-variable function is a vector field in ℝ3. A gradient field is a vector field that can be written as the gradient of a function, and we have the following definition.
DEFINITION: Gradient Field
A vector field ⇀F in ℝ2 or in ℝ3 is a gradient field if there exists a scalar function f such that ⇀∇f=⇀F.
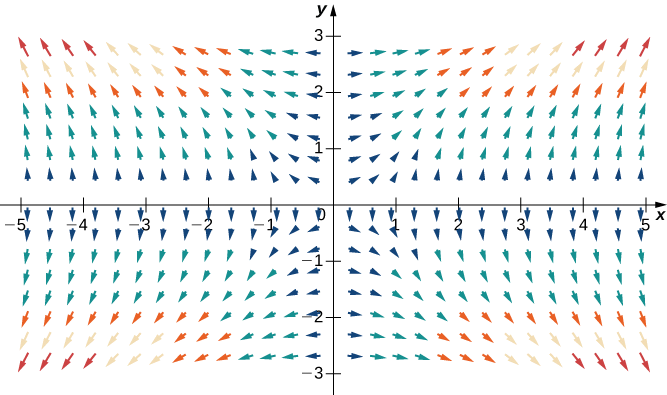
Example 5.2.9: Sketching a Gradient Vector Field
Use technology to plot the gradient vector field of f(x,y)=x2y2.
Solution
The gradient of f is ⇀∇f(x,y)=⟨2xy2,2x2y⟩. To sketch the vector field, use a computer algebra system such as Mathematica. Figure 5.2.8 shows ⇀∇f.
Exercise 5.2.9
Use technology to plot the gradient vector field of f(x,y)=sinxcosy.
- Hint
-
Find the gradient of f.
- Answer
-
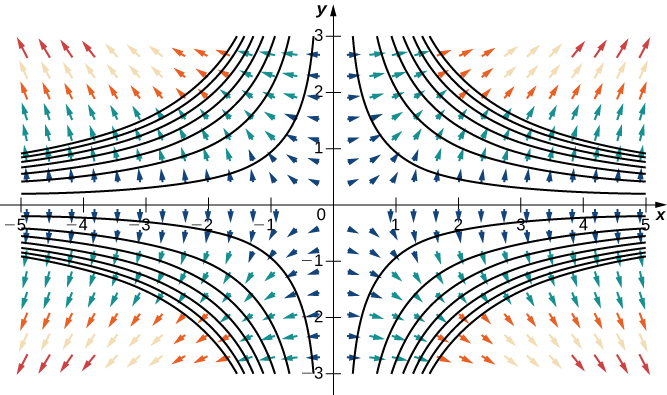
Consider the function f(x,y)=x2y2 from Example 5.2.9. Figure 5.2.9 shows the level curves of this function overlaid on the function’s gradient vector field. The gradient vectors are perpendicular to the level curves, and the magnitudes of the vectors get larger as the level curves get closer together, because closely grouped level curves indicate the graph is steep, and the magnitude of the gradient vector is the largest value of the directional derivative. Therefore, you can see the local steepness of a graph by investigating the corresponding function’s gradient field.
As we learned earlier, a vector field ⇀F is a conservative vector field, or a gradient field if there exists a scalar function f such that ⇀∇f=⇀F. In this situation, f is called a potential function for ⇀F. Conservative vector fields arise in many applications, particularly in physics. The reason such fields are called conservative is that they model forces of physical systems in which energy is conserved. We study conservative vector fields in more detail later in this chapter.
You might notice that, in some applications, a potential function f for ⇀F is defined instead as a function such that −⇀∇f=⇀F. This is the case for certain contexts in physics, for example.
Example 5.2.10: Verifying a Potential Function
Is f(x,y,z)=x2yz−sin(xy) a potential function for vector field
⇀F(x,y,z)=⟨2xyz−ycos(xy),x2z−xcos(xy),x2y⟩?
Solution
We need to confirm whether ⇀∇f=⇀F. We have
fx(x,y)=2xyz−ycos(xy)fy(x,y)=x2z−xcos(xy)fz(x,y)=x2y.
Therefore, ⇀∇f=⇀F and f is a potential function for ⇀F.
Exercise 5.2.10
Is f(x,y,z)=x2cos(yz)+y2z2 a potential function for ⇀F(x,y,z)=⟨2xcos(yz),−x2zsin(yz)+2yz2,y2⟩?
- Hint
-
Compute the gradient of f.
- Answer
-
No
Example 5.2.11: Verifying a Potential Function
The velocity of a fluid is modeled by field ⇀v(x,y)=⟨xy,x22−y⟩. Verify that f(x,y)=x2y2−y22 is a potential function for ⇀v.
Solution
To show that f is a potential function, we must show that ⇀∇f=⇀v. Note that fx(x,y)=xy and fy(x,y)=x22−y. Therefore, ⇀∇f(x,y)=⟨xy,x22−y⟩ and f is a potential function for ⇀v (Figure 5.2.10).

Exercise 5.2.11
Verify that f(x,y)=x2y2+x is a potential function for velocity field ⇀v(x,y)=⟨3x2y2+1,2x3y⟩.
- Hint
-
Calculate the gradient.
- Answer
-
⇀∇f(x,y)=⇀v(x,y)
If ⇀F is a conservative vector field, then there is at least one potential function f such that ⇀∇f=⇀F. But, could there be more than one potential function? If so, is there any relationship between two potential functions for the same vector field? Before answering these questions, let’s recall some facts from single-variable calculus to guide our intuition. Recall that if k(x) is an integrable function, then k has infinitely many antiderivatives. Furthermore, if ⇀F and ⇀G are both antiderivatives of k, then ⇀F and ⇀G differ only by a constant. That is, there is some number C such that ⇀F(x)=⇀G(x)+C.
Now let ⇀F be a conservative vector field and let f and g be potential functions for ⇀F. Since the gradient is like a derivative, ⇀F being conservative means that ⇀F is “integrable” with “antiderivatives” f and g. Therefore, if the analogy with single-variable calculus is valid, we expect there is some constant C such that f(x)=g(x)+C. The next theorem says that this is indeed the case.
To state the next theorem with precision, we need to assume the domain of the vector field is connected and open. To be connected means if P1 and P2 are any two points in the domain, then you can walk from P1 to P2 along a path that stays entirely inside the domain.
UNIQUENESS OF POTENTIAL FUNCTIONS
Let ⇀F be a conservative vector field on an open and connected domain and let f and g be functions such that ⇀∇f=⇀F and ⇀∇g=⇀G. Then, there is a constant C such that f=g+C.
Proof
Since f and g are both potential functions for ⇀F, then ⇀∇(f−g)=⇀∇f−⇀∇g=⇀F−⇀F=⇀0. Let h=f−g, then we have ⇀∇h=⇀0.We would like to show that h is a constant function.
Assume h is a function of x and y (the logic of this proof extends to any number of independent variables). Since ⇀∇h=⇀0, we have hx(x,y)=0 and hy(x,y)=0. The expression hx(x,y)=0 implies that h is a constant function with respect to x—that is, h(x,y)=k1(y) for some function k1. Similarly, hy(x,y)=0 implies h(x,y)=k2(x) for some function k2. Therefore, function h depends only on y and also depends only on x. Thus, h(x,y)=C for some constant C on the connected domain of ⇀F. Note that we really do need connectedness at this point; if the domain of ⇀F came in two separate pieces, then k could be a constant C1 on one piece but could be a different constant C2 on the other piece. Since f−g=h=C, we have that f=g+C, as desired.
◻
Conservative Vector Fields and Potential Functions
As we have learned, the Fundamental Theorem for Line Integrals says that if ⇀F is conservative, then calculating ∫C⇀F·d⇀r has two steps: first, find a potential function f for ⇀F and, second, calculate f(P1)−f(P0), where P1 is the endpoint of C and P0 is the starting point. To use this theorem for a conservative field ⇀F, we must be able to find a potential function f for ⇀F. Therefore, we must answer the following question: Given a conservative vector field ⇀F, how do we find a function f such that ⇀∇f=⇀F? Before giving a general method for finding a potential function, let’s motivate the method with an example.
Example 5.2.5: Finding a Potential Function
Find a potential function for ⇀F(x,y)=⟨2xy3,3x2y2+cos(y)⟩, thereby showing that ⇀F is conservative.
Solution
Suppose that f(x,y) is a potential function for ⇀F. Then, ⇀∇f=⇀F, and therefore
fx(x,y)=2xy3andfy(x,y)=3x2y2+cosy.
Integrating the equation fx(x,y)=2xy3 with respect to x yields the equation
f(x,y)=x2y3+h(y).
Notice that since we are integrating a two-variable function with respect to x, we must add a constant of integration that is a constant with respect to x, but may still be a function of y. The equation f(x,y)=x2y3+h(y) can be confirmed by taking the partial derivative with respect to x:
∂f∂x=∂∂x(x2y3)+∂∂x(h(y))=2xy3+0=2xy3.
Since f is a potential function for ⇀F,
fy(x,y)=3x2y2+cos(y),
and therefore
3x2y2+g′(y)=3x2y2+cos(y).
This implies that h′(y)=cosy, so h(y)=siny+C. Therefore, any function of the form f(x,y)=x2y3+sin(y)+C is a potential function. Taking, in particular, C=0 gives the potential function f(x,y)=x2y3+sin(y).
To verify that f is a potential function, note that ⇀∇f(x,y)=⟨2xy3,3x2y2+cosy⟩=⇀F.
Exercise 5.2.5
Find a potential function for ⇀F(x,y)=⟨exy3+y,3exy2+x⟩.
- Hint
-
Follow the steps in Example 5.2.5.
- Answer
-
f(x,y)=exy3+xy
The logic of the previous example extends to finding the potential function for any conservative vector field in ℝ2. Thus, we have the following problem-solving strategy for finding potential functions:
PROBLEM-SOLVING STRATEGY: FINDING A POTENTIAL FUNCTION FOR A CONSERVATIVE VECTOR FIELD ⇀F(x,y)=⟨P(x,y),Q(x,y)⟩
- Integrate P with respect to x. This results in a function of the form g(x,y)+h(y), where h(y) is unknown.
- Take the partial derivative of g(x,y)+h(y) with respect to y, which results in the function gy(x,y)+h′(y).
- Use the equation gy(x,y)+h′(y)=Q(x,y) to find h′(y).
- Integrate h′(y) to find h(y).
- Any function of the form f(x,y)=g(x,y)+h(y)+C, where C is a constant, is a potential function for ⇀F.
We can adapt this strategy to find potential functions for vector fields in ℝ3, as shown in the next example.
Example 5.2.6: Finding a Potential Function in ℝ3
Find a potential function for F(x,y,z)=⟨2xy,x2+2yz3,3y2z2+2z⟩, thereby showing that ⇀F is conservative.
Solution
Suppose that f is a potential function. Then, ⇀∇f=⇀F and therefore fx(x,y,z)=2xy. Integrating this equation with respect to x yields the equation f(x,y,z)=x2y+g(y,z) for some function g. Notice that, in this case, the constant of integration with respect to x is a function of y and z.
Since f is a potential function,
x2+2yz3=fy(x,y,z)=x2+gy(y,z).
Therefore,
gy(y,z)=2yz3.
Integrating this function with respect to y yields
g(y,z)=y2z3+h(z)
for some function h(z) of z alone. (Notice that, because we know that g is a function of only y and z, we do not need to write g(y,z)=y2z3+h(x,z).) Therefore,
f(x,y,z)=x2y+g(y,z)=x2y+y2z3+h(z).
To find f, we now must only find h. Since f is a potential function,
3y2z2+2z=gz(y,z)=3y2z2+h′(z).
This implies that h′(z)=2z, so h(z)=z2+C. Letting C=0 gives the potential function
f(x,y,z)=x2y+y2z3+z2.
To verify that f is a potential function, note that ⇀∇f(x,y,z)=⟨2xy,x2+2yz3,3y2z2+2z⟩=⇀F(x,y,z).
Exercise 5.2.6
Find a potential function for ⇀F(x,y,z)=⟨12x2,cosycosz,1−sinysinz⟩.
- Hint
-
Following Example 5.2.6, begin by integrating with respect to x.
- Answer
-
f(x,y,z)=4x3+sinycosz+z
We can apply the process of finding a potential function to a gravitational force. Recall that, if an object has unit mass and is located at the origin, then the gravitational force in ℝ2 that the object exerts on another object of unit mass at the point (x,y) is given by vector field
⇀F(x,y)=−G⟨x(x2+y2)3/2,y(x2+y2)3/2⟩,
where G is the universal gravitational constant. In the next example, we build a potential function for ⇀F, thus confirming what we already know: that gravity is conservative.
Example 5.2.7: Finding a Potential Function
Find a potential function f for ⇀F(x,y)=−G⟨x(x2+y2)3/2,y(x2+y2)3/2⟩.
Solution
Suppose that f is a potential function. Then, ⇀∇f=⇀F and therefore
fx(x,y)=−Gx(x2+y2)3/2.
To integrate this function with respect to x, we can use u-substitution. If u=x2+y2, then du2=xdx, so
∫−Gx(x2+y2)3/2dx=∫−G2u3/2du=G√u+h(y)=G√x2+y2+h(y)
for some function h(y). Therefore,
f(x,y)=G√x2+y2+h(y).
Since f is a potential function for ⇀F,
fy(x,y)=−Gy(x2+y2)3/2
Since f(x,y)=G√x2+y2+h(y), fy(x,y) also equals −Gy(x2+y2)3/2+h′(y).
Therefore,
−Gy(x2+y2)3/2+h′(y)=−Gy(x2+y2)3/2,
which implies that h′(y)=0. Thus, we can take h(y) to be any constant; in particular, we can let h(y)=0. The function
f(x,y)=G√x2+y2
is a potential function for the gravitational field ⇀F. To confirm that f is a potential function, note that
⇀∇f(x,y)=⟨−12G(x2+y2)3/2(2x),−12G(x2+y2)3/2(2y)⟩=⟨−Gx(x2+y2)3/2,−Gy(x2+y2)3/2⟩=⇀F(x,y).
Exercise 5.2.7
Find a potential function f for the three-dimensional gravitational force ⇀F(x,y,z)=⟨−Gx(x2+y2+z2)3/2,−Gy(x2+y2+z2)3/2,−Gz(x2+y2+z2)3/2⟩.
- Hint
-
Follow the Problem-Solving Strategy.
- Answer
-
f(x,y,z)=G√x2+y2+z2
Testing a Vector Field
Until now, we have worked with vector fields that we know are conservative, but if we are not told that a vector field is conservative, we need to be able to test whether it is conservative. Recall that, if ⇀F is conservative, then ⇀F has the cross-partial property (see The Cross-Partial Property of Conservative Vector Fields). That is, if ⇀F=⟨P,Q,R⟩ is conservative, then Py=Qx, Pz=Rx, and Qz=Ry. So, if ⇀F has the cross-partial property, then is ⇀F conservative? If the domain of ⇀F is open and simply connected, then the answer is yes.
Theorem: THE CROSS-PARTIAL TEST FOR CONSERVATIVE FIELDS
If ⇀F=⟨P,Q,R⟩ is a vector field on an open, simply connected region D and Py=Qx, Pz=Rx, and Qz=Ry throughout D, then ⇀F is conservative.
Although a proof of this theorem is beyond the scope of the text, we can discover its power with some examples. Later, we see why it is necessary for the region to be simply connected.
Combining this theorem with the cross-partial property, we can determine whether a given vector field is conservative:
Theorem: CROSS-PARTIAL PROPERTY OF CONSERVATIVE FIELDS
Let ⇀F=⟨P,Q,R⟩ be a vector field on an open, simply connected region D. Then Py=Qx, Pz=Rx, and Qz=Ry throughout D if and only if ⇀F is conservative.
The version of this theorem in ℝ2 is also true. If ⇀F(x,y)=⟨P,Q⟩ is a vector field on an open, simply connected domain in ℝ2, then ⇀F is conservative if and only if Py=Qx.
Example 5.2.8: Determining Whether a Vector Field Is Conservative
Determine whether vector field ⇀F(x,y,z)=⟨xy2z,x2yz,z2⟩ is conservative.
Solution
Note that the domain of ⇀F is all of ℝ2 and ℝ3 is simply connected. Therefore, we can use The Cross-Partial Property of Conservative Vector Fields to determine whether ⇀F is conservative. Let
P(x,y,z)=xy2z
Q(x,y,z)=x2yz
and
R(x,y,z)=z2.
Since Qz(x,y,z)=x2y and Ry(x,y,z)=0, the vector field is not conservative.
Example 5.2.9: Determining Whether a Vector Field Is Conservative
Determine vector field ⇀F(x,y)=⟨xln(y),x22y⟩ is conservative.
Solution
Note that the domain of ⇀F is the part of ℝ2 in which y>0. Thus, the domain of ⇀F is part of a plane above the x-axis, and this domain is simply connected (there are no holes in this region and this region is connected). Therefore, we can use The Cross-Partial Property of Conservative Vector Fields to determine whether ⇀F is conservative. Let
P(x,y)=xln(y)and Q(x,y)=x22y.
Then Py(x,y)=xy=Qx(x,y) and thus ⇀F is conservative.
Exercise 5.2.8
Determine whether ⇀F(x,y)=⟨sinxcosy,cosxsiny⟩ is conservative.
- Hint
-
Use The Cross-Partial Property of Conservative Vector Fields from the previous section.
- Answer
-
It is conservative.
When using The Cross-Partial Property of Conservative Vector Fields, it is important to remember that a theorem is a tool, and like any tool, it can be applied only under the right conditions. In the case of The Cross-Partial Property of Conservative Vector Fields, the theorem can be applied only if the domain of the vector field is simply connected.
To see what can go wrong when misapplying the theorem, consider the vector field from Example 5.2.4:
⇀F(x,y)=yx2+y2ˆi+−xx2+y2ˆj.
This vector field satisfies the cross-partial property, since
∂∂y(yx2+y2)=(x2+y2)−y(2y)(x2+y2)2=x2−y2(x2+y2)2
and
∂∂x(−xx2+y2)=−(x2+y2)+x(2x)(x2+y2)2=x2−y2(x2+y2)2.
Since ⇀F satisfies the cross-partial property, we might be tempted to conclude that ⇀F is conservative. However, ⇀F is not conservative. To see this, let
⇀r(t)=⟨cost,sint⟩,0≤t≤π
be a parameterization of the upper half of a unit circle oriented counterclockwise (denote this C1) and let
⇀s(t)=⟨cost,−sint⟩,0≤t≤π
be a parameterization of the lower half of a unit circle oriented clockwise (denote this C2). Notice that C1 and C2 have the same starting point and endpoint. Since sin2t+cos2t=1,
⇀F(⇀r(t))⋅⇀r′(t)=⟨sin(t),−cos(t)⟩⋅⟨−sin(t),cos(t)⟩=−1
and
⇀F(⇀s(t))·⇀s′(t)=⟨−sint,−cost⟩·⟨−sint,−cost⟩=sin2t+cos2t=1.
Therefore,
∫C1⇀F·d⇀r=∫π0−1dt=−π
and
∫C2⇀F·d⇀r=∫π01dt=π.
Thus, C1 and C2 have the same starting point and endpoint, but ∫C1⇀F·d⇀r≠∫C2⇀F·d⇀r. Therefore, ⇀F is not independent of path and ⇀F is not conservative.
To summarize: ⇀F satisfies the cross-partial property and yet ⇀F is not conservative. What went wrong? Does this contradict The Cross-Partial Property of Conservative Vector Fields? The issue is that the domain of ⇀F is all of ℝ2 except for the origin. In other words, the domain of ⇀F has a hole at the origin, and therefore the domain is not simply connected. Since the domain is not simply connected, The Cross-Partial Property of Conservative Vector Fields does not apply to ⇀F.
Key Concepts
- A vector field assigns a vector ⇀F(x,y) to each point (x,y) in a subset D of ℝ2 or ℝ3. ⇀F(x,y,z) to each point (x,y,z) in a subset D of ℝ3.
- Vector fields can describe the distribution of vector quantities such as forces or velocities over a region of the plane or of space. They are in common use in such areas as physics, engineering, meteorology, oceanography.
- We can sketch a vector field by examining its defining equation to determine relative magnitudes in various locations and then drawing enough vectors to determine a pattern.
- A vector field ⇀F is called conservative if there exists a scalar function f such that ⇀∇f=⇀F.
Key Equations
- Vector field in ℝ2
⇀F(x,y)=⟨P(x,y),Q(x,y)⟩
or
⇀F(x,y)=P(x,y)ˆi+Q(x,y)ˆj - Vector field in ℝ3
⇀F(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩
or
⇀F(x,y,z)=P(x,y,z)ˆi+Q(x,y,z)ˆj+R(x,y,z)ˆk
Glossary
- conservative field
- a vector field for which there exists a scalar function f such that ⇀∇f=⇀F
- gradient field
- a vector field ⇀F for which there exists a scalar function f such that ⇀∇f=⇀F; in other words, a vector field that is the gradient of a function; such vector fields are also called conservative
- potential function
- a scalar function f such that ⇀∇f=⇀F
- radial field
- a vector field in which all vectors either point directly toward or directly away from the origin; the magnitude of any vector depends only on its distance from the origin
- rotational field
- a vector field in which the vector at point (x,y) is tangent to a circle with radius r=√x2+y2; in a rotational field, all vectors flow either clockwise or counterclockwise, and the magnitude of a vector depends only on its distance from the origin
- unit vector field
- a vector field in which the magnitude of every vector is 1
- vector field
- measured in ℝ2, an assignment of a vector ⇀F(x,y) to each point (x,y) of a subset D of ℝ2; in ℝ3, an assignment of a vector ⇀F(x,y,z) to each point (x,y,z) of a subset D of ℝ3
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


