3.3: Solve Mixture Applications with Systems of Equations
- Last updated
- Dec 16, 2019
- Save as PDF
- Page ID
- 29054
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Solve mixture applications
- Solve interest applications
- Solve applications of cost and revenue functions
Before you get started, take this readiness quiz.
Solve Mixture Applications
Mixture application involve combining two or more quantities. When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:
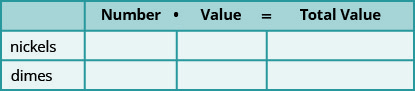
Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n, or if we would let d be the number of dimes and write the number of nickels in terms of d.
Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.
For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.
Example 3.3.1
Translate to a system of equations and solve:
A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?
- Answer
-
Step 1. Read the problem. We will create a table to organize the information. Step 2. Identify what we are looking for. We are looking for the number of adult tickets
and the number of child tickets sold.Step 3. Name what we are looking for. Let a=the number of adult tickets.
c=the number of child ticketsA table will help us organize the data.
We have two types of tickets, adult and child.Write in a and c for the number of tickets. Write the total number of tickets sold at the bottom
of the Number column.Altogether 1,363 were sold. Write the value of each type of ticket in the
Value column.The value of each adult ticket is $12.
The value of each child tickets is $7.The number times the value gives the total value,
so the total value of adult tickets is a·12=12a,
and the total value of child tickets is c·7=7c.Fill in the Total Value column. Altogether the total value of the tickets was $12,146. 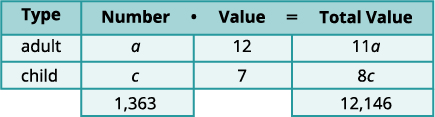
Step 4. Translate into a system of equations. The Number column and the Total value column
give us the system of equations.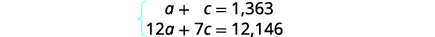
We will use the elimination method to solve
this system. Multiply the first equation by −7.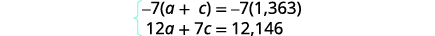
Simplify and add, then solve for a. 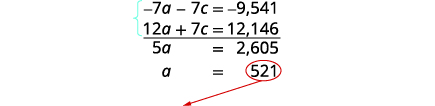
Substitute a=521 into the first equation, then
solve for c.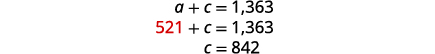
Step 6. Check the answer in the
problem.
521 adult at $12 per ticket makes $ 6,252
842 child at $7 per ticket makes $58,994
The total receipts are $12,146✓Step 7. Answer the question. The science center sold 521 adult tickets and
842 child tickets.
Example 3.3.2
Translate to a system of equations and solve:
The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?
- Answer
-
206 adults, 347 children
Example 3.3.3
Translate to a system of equations and solve:
The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?
- Answer
-
42 adults, 105 children
In the next example, we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.
Example 3.3.4
Translate to a system of equations and solve:
Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?
- Answer
-
Step 1. Read the problem.
We will create a table to organize the information.Step 2. Identify what we are looking for. We are looking for the number of
nickels and the number of dimes.Step 3. Name what we are looking for. Let n=the number of nickels.
d=the number of dimesA table will help us organize the data.
We have two types of coins, nickels and dimes.Write n and d for the number of
each type of coin.Fill in the Value column with the value of each
type of coin.The value of each nickel is $0.05.
The value of each dime is $0.10.The number times the value gives the total
value, so, the total value of the nickels is
n(0.05)=0.05n and the total value of dimes is
d(0.10)=0.10d.
Altogether the total value of the coins is $8.10.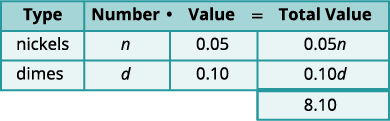
Step 4. Translate into a system of equations. The Total Value column gives one equation. 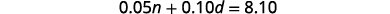
We also know the number of dimes is 9 less than
twice the number of nickels.Translate to get the second equation. 
Now we have the system to solve. 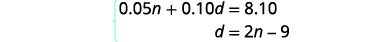
Step 5. Solve the system of equations
We will use the substitution method.Substitute d=2n−9 into the first equation. 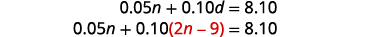
Simplify and solve for n. 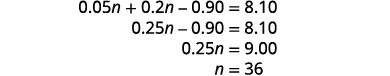
To find the number of dimes, substitute
n=36 into the second equation.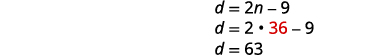
Step 6. Check the answer in the problem
63 dimes at $0.10=$6.30
36 nickels at $0.05=$1.80
Total =$8.10✓Step 7. Answer the question. Juan has 36 nickels and 63 dimes.
Example 3.3.5
Translate to a system of equations and solve:
Matilda has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?
- Answer
-
13 dimes and 29 quarters
Example 3.3.6
Translate to a system of equations and solve:
Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?
- Answer
-
19 quarters and 51 nickels
Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.
Example 3.3.7
Translate to a system of equations and solve:
Carson wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60. per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?
- Answer
-
Step 1. Read the problem.
We will create a table to organize the information.Step 2. Identify what we are looking for. We are looking for the number of pounds of
nuts and the number of pounds of chocolate
chips.Step 3. Name what we are looking for. Let n=the number of pound of nuts.
c=the number of pounds of chipsCarson will mix nuts and chocolate chips to get
trail mix.
Write in n and c for the number of pounds of
nuts and chocolate chips.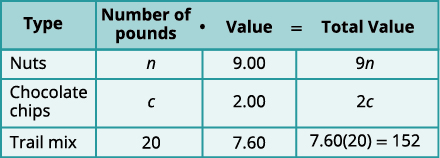
There will be 20 pounds of trail mix.
Put the price per pound of each item in
the Value column.
Fill in the last column using
Number•Value=Total ValueStep 4. Translate into a system of equations.
We get the equations from the Number
and Total Value columns.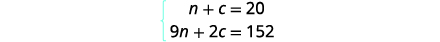
Step 5. Solve the system of equations
We will use elimination to solve the system.
Multiply the first equation by −2 to eliminate c.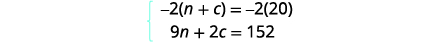
Simplify and add.
Solve for n.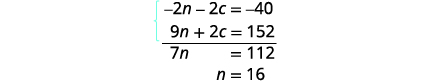
To find the number of pounds of chocolate
chips, substitute n=16 into the first equation,
then solve for c.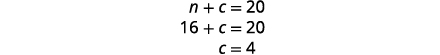
Step 6. Check the answer in the problem.
16+4=20✓9·16+2·4=152✓Step 7. Answer the question. Carson should mix 16 pounds of nuts with 4
pounds of chocolate chips to create the trail
mix.
Example 3.3.8
Translate to a system of equations and solve:
Greta wants to make 5 pounds of a nut mix using peanuts and cashews. Her budget requires the mixture to cost her $6 per pound. Peanuts are $4 per pound and cashews are $9 per pound. How many pounds of peanuts and how many pounds of cashews should she use?
- Answer
-
3 pounds peanuts and 2 pounds cashews
Example 3.3.9
Translate to a system of equations and solve:
Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?
- Answer
-
10 pounds of beans, 10 pounds of ground beef
Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentrated household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.
For these kinds of mixture problems, we’ll use “percent” instead of “value” for one of the columns in our table.
Example 3.3.10
Translate to a system of equations and solve:
Sasheena is lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?
- Answer
-
Step 1. Read the problem.
A figure may help us visualize the
situation, then we will create a table to
organize the information.Sasheena must mix some of the 25 solution and
some of the 50 solution together to get 200 ml of
the 40 solution.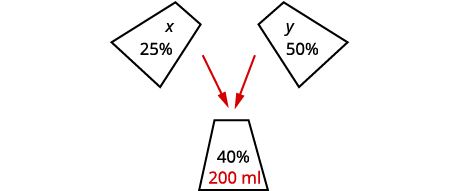
Step 2. Identify what we are looking for. We are looking for how much of each solution she
needs.Step 3. Name what we are looking for. Let x=number of ml of 25
\(y= \text{number of }ml\text{ of }50%\text{ solution\)A table will help us organize the data. She will
mix x ml of 25 with y ml of 50 to get 200 ml
of 40 solution. We write the percents as decimals
in the chart.
We multiply the number of units times the
concentration to get the total amount of
sulfuric acid in each solution.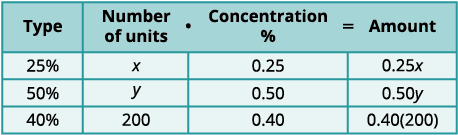
Step 4. Translate into a system of
equations.
We get the equations from the Number
column and the Amount column.
Now we have the system.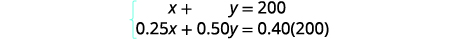
Step 5. Solve the system of equations
We will solve the system by elimination.
Multiply the first equation by −0.5 to
eliminate y.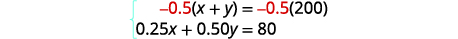
Simplify and add to solve for x. 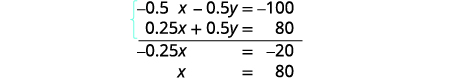
To solve for y, substitute x=80 into the first
equation.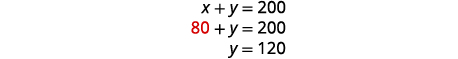
Step 6. Check the answer in the problem.
80+120=200✓0.25(80)+0.50(120)=200✓Yes!Step 7. Answer the question. Sasheena should mix 80 ml of the 25 solution with
120 ml of the 50 solution to get the 200 ml of the
40 solution.
Example 3.3.11
Translate to a system of equations and solve:
LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?
- Answer
-
120 ml of 25% solution and 30 ml of 50% solution
Example 3.3.12
Translate to a system of equations and solve:
Anatole needs to make 250 milliliters of a 25% solution of hydrochloric acid for a lab experiment. The lab only has a 10% solution and a 40% solution in the storeroom. How much of the 10% and how much of the 40% solutions should he mix to make the 25% solution?
- Answer
-
125 ml of 10% solution and 125 ml of 40% solution
Solve Interest Applications
The formula to model simple interest applications is I=Prt. Interest, I, is the product of the principal, P, the rate, r, and the time, t. In our work here, we will calculate the interest earned in one year, so t will be 1.
We modify the column titles in the mixture table to show the formula for interest, as you’ll see in the next example.
Translate to a system of equations and solve:
Adnan has $40,000 to invest and hopes to earn 7.1 interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earns 3% per year. How much money should he put into each fund?
- Answer
-
Did you notice that the Principal column represents the total amount of money invested while the Interest column represents only the interest earned? Likewise, the first equation in our system, s+b=40,000, represents the total amount of money invested and the second equation, 0.08s+0.03b=0.071(40,000), represents the interest earned.Step 1. Read the problem. A chart will help us organize the information. Step 2. Identify what we are looking for. We are looking for the amount to invest in each fund. Step 3. Name what we are looking for. Let s=the amount invested in stocks.
b=the amount invested in stocksWrite the interest rate as a decimal for
each fund.
Multiply: Principal · Rate · Time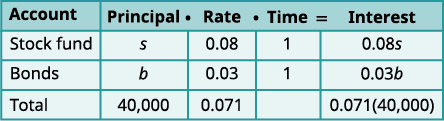
Step 4. Translate into a system of
equations.
We get our system of equations from
the Principal column and the
Interest column.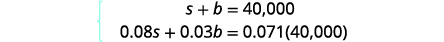
Step 5. Solve the system of equations
by elimination.
Multiply the top equation by −0.03.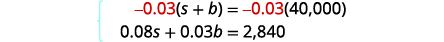
Simplify and add to solve for s. 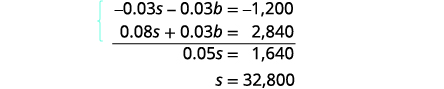
To find b, substitute s = 32,800 into
the first equation.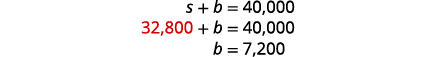
Step 6. Check the answer in the
problem.We leave the check to you. Step 7. Answer the question. Adnan should invest $32,800 in stock and
$7,200 in bonds.
Example 3.3.14
Translate to a system of equations and solve:
Leon had $50,000 to invest and hopes to earn 6.2 interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?
- Answer
-
$42,000 in the stock fund and $8000 in the savings account
Example 3.3.15
Translate to a system of equations and solve:
Julius invested $7000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. He earned 12.5 interest on the total investment. How much money did he put in each stock?
- Answer
-
$1750 at 11% and $5250 at 13%
The next example requires that we find the principal given the amount of interest earned.
Example 3.3.16
Translate to a system of equations and solve:
Rosie owes $21,540 on her two student loans. The interest rate on her bank loan is 10.5 and the interest rate on the federal loan is 5.9. The total amount of interest she paid last year was $1,669.68. What was the principal for each loan?
- Answer
-
Step 1. Read the problem. A chart will help us organize the information. Step 2. Identify what we are looking for. We are looking for the principal of each loan. Step 3. Name what we are looking for. Let b=the principal for the bank loan.
f=the principal on the federal loanThe total loans are $21,540. Record the interest rates as decimals
in the chart.
Multiply using the formula I = Prt to
get the Interest.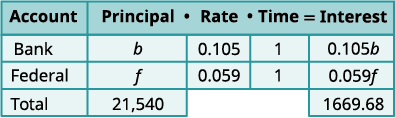
Step 4. Translate into a system of
equations.
The system of equations comes from
the Principal column and the Interest
column.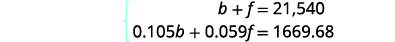
Step 5. Solve the system of equations
We will use substitution to solve.
Solve the first equation for b.
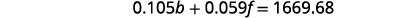
Substitute b = −f + 21.540 into
the second equation.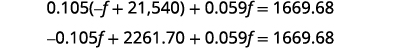
Simplify and solve for f. 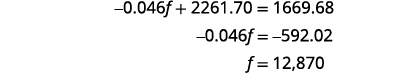
To find b, substitute f = 12,870 into the first equation. 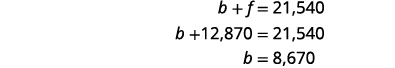
Step 6. Check the answer in the
problem.We leave the check to you. Step 7. Answer the question. The principal of the federal loan was $12,870 and
the principal for the bank loan was $8,670.
Example 3.3.17
Translate to a system of equations and solve:
Laura owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9%. The total amount of interest she paid last year was $1,066. What was the principal for each loan?
- Answer
-
Bank $4,000; Federal $14,000
Example 3.3.18
Translate to a system of equations and solve:
Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?
- Answer
-
$41,200 at 4.5%, $24,000 at 7.2%
Solve applications of cost and revenue functions
Suppose a company makes and sells x units of a product. The cost to the company is the total costs to produce x units. This is the cost to manufacture for each unit times x, the number of units manufactured, plus the fixed costs.
The revenue is the money the company brings in as a result of selling x units. This is the selling price of each unit times the number of units sold.
When the costs equal the revenue we say the business has reached the break-even point.
COST AND REVENUE FUNCTIONS
The cost function is the cost to manufacture each unit times x, the number of units manufactured, plus the fixed costs.
C(x)=(cost per unit)·x+fixed costs
The revenue function is the selling price of each unit times x, the number of units sold.
R(x)=(selling price per unit)·x
The break-even point is when the revenue equals the costs.
C(x)=R(x)
Example 3.3.19
The manufacturer of a weight training bench spends $105 to build each bench and sells them for $245. The manufacturer also has fixed costs each month of $7,000.
ⓐ Find the cost function C when x benches are manufactured.
ⓑ Find the revenue function R when x benches are sold.
ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.
ⓓ Find the break-even point. Interpret what the break-even point means.
- Answer
-
ⓐ The manufacturer has $7,000 of fixed costs no matter how many weight training benches it produces. In addition to the fixed costs, the manufacturer also spends $105 to produce each bench. Suppose x benches are sold.
Write the general Cost function formula.C(x)=(cost per unit)·x+fixed costsSubstitute in the cost values.C(x)=105x+7000
ⓑ The manufacturer sells each weight training bench for $245. We get the total revenue by multiplying the revenue per unit times the number of units sold.
Write the general Revenue function.C(x)=(selling price per unit)·xSubstitute in the revenue per unit.R(x)=245x
ⓒ Essentially we have a system of linear equations. We will show the graph of the system as this helps make the idea of a break-even point more visual.
{C(x)=105x+7000R(x)=245xor{y=105x+7000y=245x
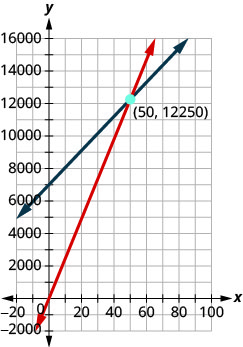
ⓓ To find the actual value, we remember the break-even point occurs when costs equal revenue.
Write the break-even formula.C(x)=R(x)105x+7000=245xSolve.7000=140x50=x
When 50 benches are sold, the costs equal the revenue.

When 50 benches are sold, the revenue and costs are both $12,250. Notice this corresponds to the ordered pair (50,12250).
Example 3.3.20
The manufacturer of a weight training bench spends $15 to build each bench and sells them for $32. The manufacturer also has fixed costs each month of $25,500.
ⓐ Find the cost function C when x benches are manufactured.
ⓑ Find the revenue function R when x benches are sold.
ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.
ⓓ Find the break-even point. Interpret what the break-even point means.
- Answer
-
ⓐ C(x)=15x+25,500
ⓑ R(x)=32x
ⓒ
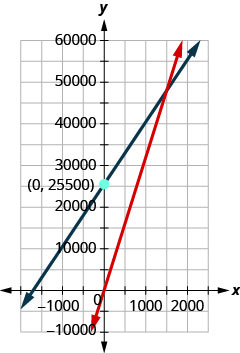
ⓓ 1,5001,500; when 1,500 benches are sold, the cost and revenue will be both 48,000
Example 3.3.21
The manufacturer of a weight training bench spends $120 to build each bench and sells them for $170. The manufacturer also has fixed costs each month of $150,000.
ⓐ Find the cost function C when x benches are manufactured.
ⓑ Find the revenue function R when x benches are sold.
ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.
ⓓ Find the break-even point. Interpret what the break-even point means.
- Answer
-
ⓐ C(x)=120x+150,000
ⓑ R(x)=170x
ⓒ
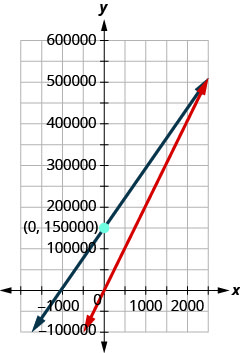
ⓓ 3,000; when 3,000 benches are sold, the revenue and costs are both $510,000
Access this online resource for additional instruction and practice with interest and mixtures.
- Interest and Mixtures
Key Concepts
- Cost function: The cost function is the cost to manufacture each unit times x, the number of units manufactured, plus the fixed costs.
C(x)=(cost per unit)·x+fixed costs
- Revenue: The revenue function is the selling price of each unit times x, the number of units sold.
R(x)=(selling price per unit)·x
- Break-even point: The break-even point is when the revenue equals the costs.
C(x)=R(x)
Glossary
- cost function
- The cost function is the cost to manufacture each unit times xx, the number of units manufactured, plus the fixed costs; C(x) = (cost per unit)x + fixed costs.
- revenue
- The revenue is the selling price of each unit times x, the number of units sold; R(x) = (selling price per unit)x.
- break-even point
- The point at which the revenue equals the costs is the break-even point; C(x)=R(x).


