3.4: Solve Systems of Equations with Three Variables
- Last updated
- Dec 16, 2019
- Save as PDF
- Page ID
- 29055
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Determine whether an ordered triple is a solution of a system of three linear equations with three variables
- Solve a system of linear equations with three variables
- Solve applications using systems of linear equations with three variables
Before you get started, take this readiness quiz.
- Evaluate 5x−2y+3z when x=−2,y=−4, and z=3.
If you missed this problem, review [link]. - Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. {−2x+y=−11x+3y=9
If you missed this problem, review [link]. - Classify the equations as a conditional equation, an identity, or a contradiction and then state the solution. {7x+8y=43x−5y=27
If you missed this problem, review [link].
Determine Whether an Ordered Triple is a Solution of a System of Three Linear Equations with Three Variables
In this section, we will extend our work of solving a system of linear equations. So far we have worked with systems of equations with two equations and two variables. Now we will work with systems of three equations with three variables. But first let's review what we already know about solving equations and systems involving up to two variables.
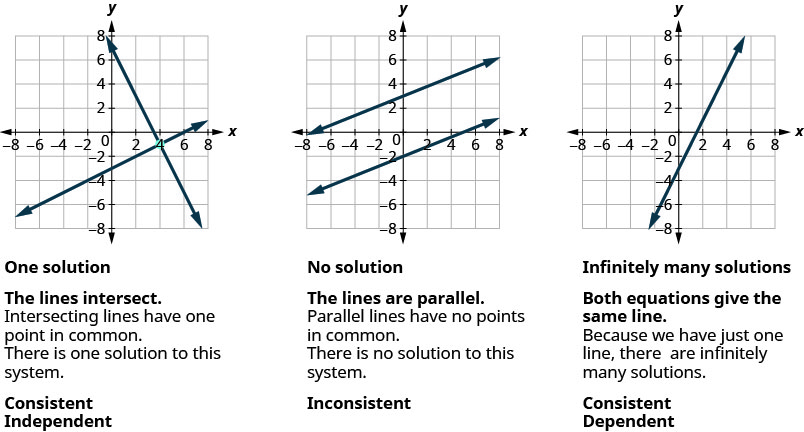
We learned earlier that the graph of a linear equation, ax+by=c, is a line. Each point on the line, an ordered pair (x,y), is a solution to the equation. For a system of two equations with two variables, we graph two lines. Then we can see that all the points that are solutions to each equation form a line. And, by finding what the lines have in common, we’ll find the solution to the system.
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions
We know when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.
Similarly, for a linear equation with three variables ax+by+cz=d,ax+by+cz=d, every solution to the equation is an ordered triple, (x,y,z)(x,y,z)that makes the equation true.
LINEAR EQUATION IN THREE VARIABLES
A linear equation with three variables, where a, b, c, and d are real numbers and a, b, and c are not all 0, is of the form
ax+by+cz=d
Every solution to the equation is an ordered triple, (x,y,z) that makes the equation true.
All the points that are solutions to one equation form a plane in three-dimensional space. And, by finding what the planes have in common, we’ll find the solution to the system.
When we solve a system of three linear equations represented by a graph of three planes in space, there are three possible cases.

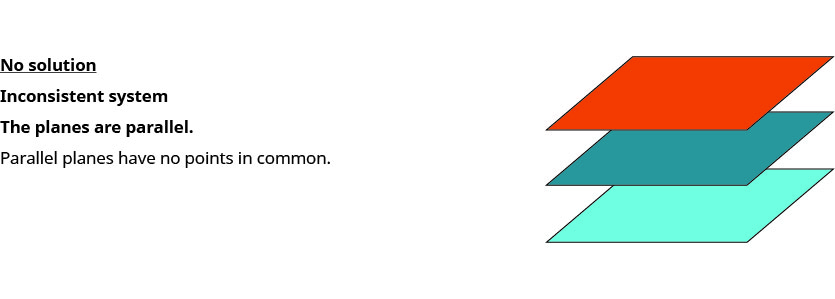






To solve a system of three linear equations, we want to find the values of the variables that are solutions to all three equations. In other words, we are looking for the ordered triple (x,y,z) that makes all three equations true. These are called the solutions of the system of three linear equations with three variables.
SolutionS OF A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES
Solutions of a system of equations are the values of the variables that make all the equations true. A solution is represented by an ordered triple (x,y,z).
To determine if an ordered triple is a solution to a system of three equations, we substitute the values of the variables into each equation. If the ordered triple makes all three equations true, it is a solution to the system.
Example 3.4.1
Determine whether the ordered triple is a solution to the system: {x−y+z=22x−y−z=−62x+2y+z=−3
ⓐ (−2,−1,3) ⓑ (−4,−3,4)
- Answer
-
ⓐ
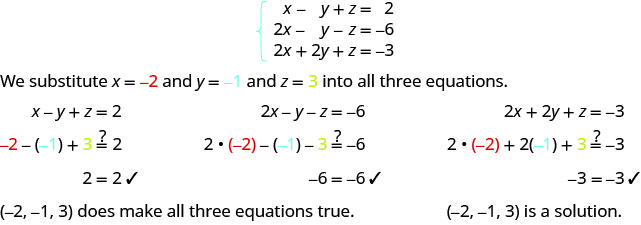
ⓑ
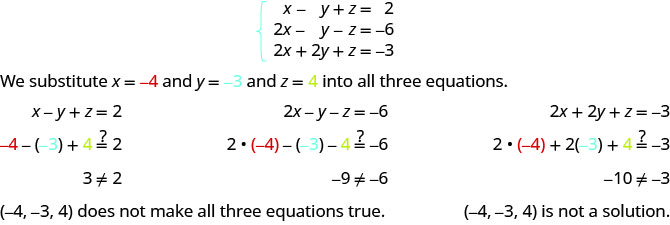
Example 3.4.2
Determine whether the ordered triple is a solution to the system: {3x+y+z=2x+2y+z=−33x+y+2z=4
ⓐ (1,−3,2) ⓑ (4,−1,−5)
- Answer
-
ⓐ yes ⓑ no
Example 3.4.3
Determine whether the ordered triple is a solution to the system: {x−3y+z=−5−3x−y−z=12x−2y+3z=1
ⓐ (2,−2,3) ⓑ (−2,2,3)
- Answer
-
ⓐ no ⓑ yes
Solve a System of Linear Equations with Three Variables
To solve a system of linear equations with three variables, we basically use the same techniques we used with systems that had two variables. We start with two pairs of equations and in each pair we eliminate the same variable. This will then give us a system of equations with only two variables and then we know how to solve that system!
Next, we use the values of the two variables we just found to go back to the original equation and find the third variable. We write our answer as an ordered triple and then check our results.
Example 3.4.4: How to Solve a System of Equations With Three Variables by Elimination
Solve the system by elimination: {x−2y+z=32x+y+z=43x+4y+3z=−1
- Answer
-






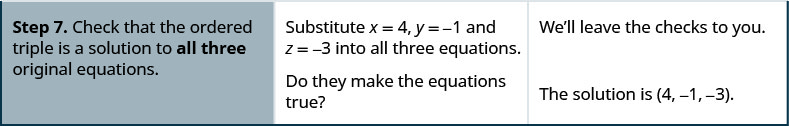
Example 3.4.5
Solve the system by elimination: {3x+y−z=22x−3y−2z=14x−y−3z=0
- Answer
-
(2,−1,3)
Example 3.4.6
Solve the system by elimination: {4x+y+z=−1−2x−2y+z=22x+3y−z=1
- Answer
-
(−2,3,4)
The steps are summarized here.
SOLVE A SYSTEM OF LINEAR EQUATIONS WITH THREE VARIABLES.
- Write the equations in standard form
- If any coefficients are fractions, clear them.
- Eliminate the same variable from two equations.
- Decide which variable you will eliminate.
- Work with a pair of equations to eliminate the chosen variable.
- Multiply one or both equations so that the coefficients of that variable are opposites.
- Add the equations resulting from Step 2 to eliminate one variable
- Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
- The two new equations form a system of two equations with two variables. Solve this system.
- Use the values of the two variables found in Step 4 to find the third variable.
- Write the solution as an ordered triple.
- Check that the ordered triple is a solution to all three original equations.
Example 3.4.7
Solve: {3x−4z=03y+2z=−32x+3y=−5
- Answer
-
{3x−4z=0(1)3y+2z=−3(2)2x+3y=−5(3)
We can eliminate z from equations (1) and (2) by multiplying equation (2) by 2 and then adding the resulting equations.
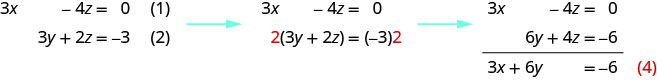
Notice that equations (3) and (4) both have the variables x and y. We will solve this new system for x and y.
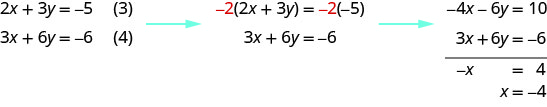
To solve for y, we substitute x=−4 into equation (3).
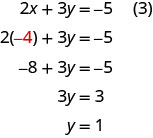
We now have x=−4 and y=1. We need to solve for z. We can substitute x=−4 into equation (1) to find z.
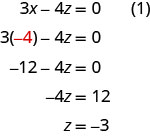
We write the solution as an ordered triple. (−4,1,−3)
We check that the solution makes all three equations true.
3x−4z=0 (1)3y+2z=−3 (2)2x+3y=−5 (3)3(−4)−4(−3)?=03(1)+2(−3)?=−32(−4)+3(1)?=−50=0✓−3=−3✓−5=−5✓The solution is (−4,1,−3)
Example 3.4.8
Solve: {3x−4z=−12y+3z=22x+3y=6
- Answer
-
(−3,4,−2)
Example 3.4.9
Solve: {4x−3z=−53y+2z=73x+4y=6
- Answer
-
(−2,3,−1)
When we solve a system and end up with no variables and a false statement, we know there are no solutions and that the system is inconsistent. The next example shows a system of equations that is inconsistent.
Example 3.4.10
Solve the system of equations: {x+2y−3z=−1x−3y+z=12x−y−2z=2
- Answer
-
{x+2y−3z=−1(1)x−3y+z=1(2)2x−y−2z=2(3)
Use equation (1) and (2) to eliminate z.
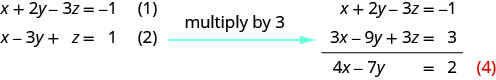
Use (2) and (3) to eliminate z again.
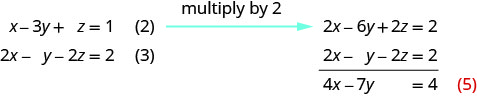
Use (4) and (5) to eliminate a variable.

There is no solution.
We are left with a false statement and this tells us the system is inconsistent and has no solution.
Example 3.4.11
Solve the system of equations: {x+2y+6z=5−x+y−2z=3x−4y−2z=1
- Answer
-
no solution
Example 3.4.12
Solve the system of equations: {2x−2y+3z=64x−3y+2z=0−2x+3y−7z=1
- Answer
-
no solution
When we solve a system and end up with no variables but a true statement, we know there are infinitely many solutions. The system is consistent with dependent equations. Our solution will show how two of the variables depend on the third.
Example 3.4.13
Solve the system of equations: {x+2y−z=12x+7y+4z=11x+3y+z=4
- Answer
-
{x+2y−z=1(1)2x+7y+4z=11(2)x+3y+z=4(3)
Use equation (1) and (3) to eliminate x.

Use equation (1) and (2) to eliminate x again.
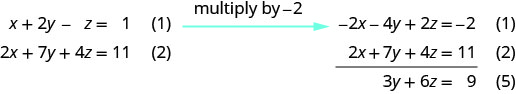
Use equation (4) and (5) to eliminate y.
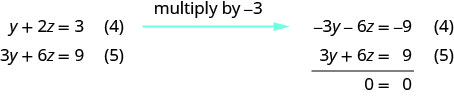
There are infinitely many solutions. Solve equation (4) for y. Represent the solution showing how x and y are dependent on z.
y+2z=3y=−2z+3Use equation (1) to solve for x. x+2y−z=1 Substitute y=−2z+3. x+2(−2z+3)−z=1x−4z+6−z=1x−5z+6=1x=5z−5 The true statement 0=0 tells us that this is a dependent system that has infinitely many solutions. The solutions are of the form (x,y,z)(x,y,z) where x=5z−5; y=−2z+3 and z is any real number.
Example 3.4.14
Solve the system by equations: {x+y−z=02x+4y−2z=63x+6y−3z=9
- Answer
-
infinitely many solutions (x,3,z) where x=z−3; y=3; z is any real number
Example 3.4.15
Solve the system by equations: {x−y−z=1−x+2y−3z=−43x−2y−7z=0
- Answer
-
infinitely many solutions (x,y,z) where x=5z−2; y=4z−3; z is any real number
Solve Applications using Systems of Linear Equations with Three Variables
Applications that are modeled by a systems of equations can be solved using the same techniques we used to solve the systems. Many of the application are just extensions to three variables of the types we have solved earlier.
Example 3.4.16
The community college theater department sold three kinds of tickets to its latest play production. The adult tickets sold for $15, the student tickets for $10 and the child tickets for $8. The theater department was thrilled to have sold 250 tickets and brought in $2,825 in one night. The number of student tickets sold is twice the number of adult tickets sold. How many of each type did the department sell?
- Answer
-
We will use a chart to organize the information. 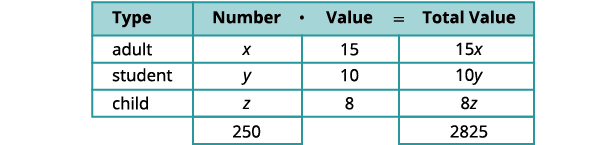
Number of students is twice number of adults. Rewrite the equation in standard form. y=2x2x−y=0 
Use equations (1) and (2) to eliminate z. 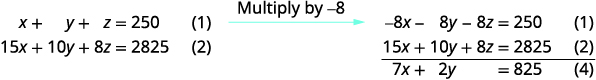
Use (3) and (4) to eliminate y. 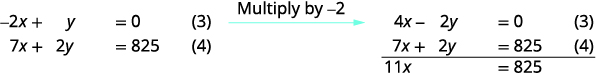
Solve for x. x=75 adult tickets Use equation (3) to find y. −2x+y=0 Substitute x=75. −2(75)+y=0−150+y=0y=150 student tickets Use equation (1) to find z. x+y+z=250 Substitute in the values
x=75, y=150.
75+150+z=250225+z=250z=25 child ticketsWrite the solution. The theater department sold 75 adult tickets,
150 student tickets, and 25 child tickets.
Example 3.4.17
The community college fine arts department sold three kinds of tickets to its latest dance presentation. The adult tickets sold for $20, the student tickets for $12 and the child tickets for $10.The fine arts department was thrilled to have sold 350 tickets and brought in $4,650 in one night. The number of child tickets sold is the same as the number of adult tickets sold. How many of each type did the department sell?
- Answer
-
The fine arts department sold 75 adult tickets, 200 student tickets, and 75 child tickets.
Example 3.4.18
The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?
- Answer
-
The soccer team sold 200 adult tickets, 300 student tickets, and 100 child tickets.
Access this online resource for additional instruction and practice with solving a linear system in three variables with no or infinite solutions.
- Solving a Linear System in Three Variables with No or Infinite Solutions
- 3 Variable Application
Key Concepts
- Linear Equation in Three Variables: A linear equation with three variables, where a, b, c, and d are real numbers and a, b,and c are not all 0, is of the form
ax+by+cz=d
Every solution to the equation is an ordered triple, (x,y,z) that makes the equation true. - How to solve a system of linear equations with three variables.
- Write the equations in standard form
If any coefficients are fractions, clear them. - Eliminate the same variable from two equations.
Decide which variable you will eliminate.
Work with a pair of equations to eliminate the chosen variable.
Multiply one or both equations so that the coefficients of that variable are opposites.
Add the equations resulting from Step 2 to eliminate one variable - Repeat Step 2 using two other equations and eliminate the same variable as in Step 2.
- The two new equations form a system of two equations with two variables. Solve this system.
- Use the values of the two variables found in Step 4 to find the third variable.
- Write the solution as an ordered triple.
- Check that the ordered triple is a solution to all three original equations.
- Write the equations in standard form
Glossary
- solutions of a system of linear equations with three variables
- The solutions of a system of equations are the values of the variables that make all the equations true; a solution is represented by an ordered triple (x,y,z).


