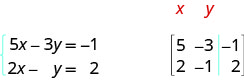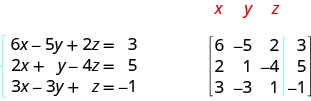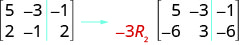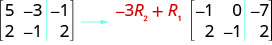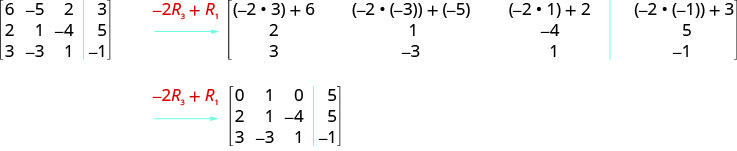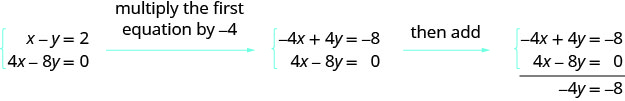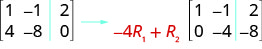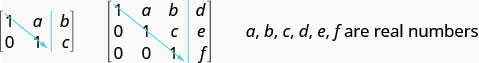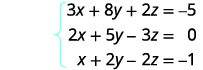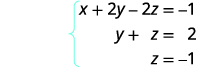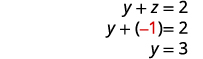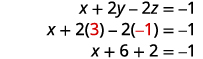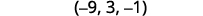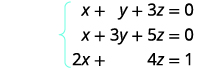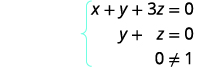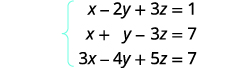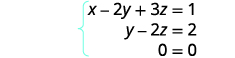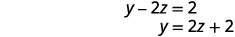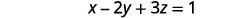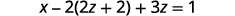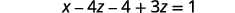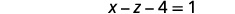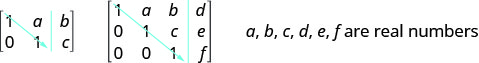Learning Objectives
By the end of this section, you will be able to:
- Write the augmented matrix for a system of equations
- Use row operations on a matrix
- Solve systems of equations using matrices
Before you get started, take this readiness quiz.
- Solve: \(3(x+2)+4=4(2x−1)+9\).
If you missed this problem, review [link].
- Solve: \(0.25p+0.25(x+4)=5.20\).
If you missed this problem, review [link].
- Evaluate when \(x=−2\) and \(y=3:2x^2−xy+3y^2\).
If you missed this problem, review [link].
Write the Augmented Matrix for a System of Equations
Solving a system of equations can be a tedious operation where a simple mistake can wreak havoc on finding the solution. An alternative method which uses the basic procedures of elimination but with notation that is simpler is available. The method involves using a matrix. A matrix is a rectangular array of numbers arranged in rows and columns.
MATRIX
A matrix is a rectangular array of numbers arranged in rows and columns.
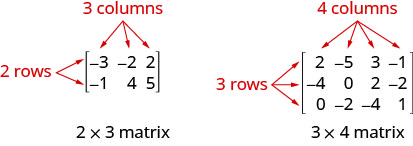
A matrix with m rows and n columns has order \(m\times n\). The matrix on the left below has 2 rows and 3 columns and so it has order \(2\times 3\). We say it is a 2 by 3 matrix.
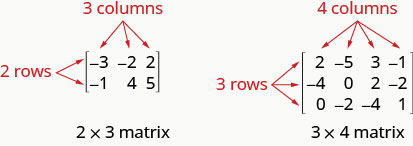
Each number in the matrix is called an element or entry in the matrix.
We will use a matrix to represent a system of linear equations. We write each equation in standard form and the coefficients of the variables and the constant of each equation becomes a row in the matrix. Each column then would be the coefficients of one of the variables in the system or the constants. A vertical line replaces the equal signs. We call the resulting matrix the augmented matrix for the system of equations.
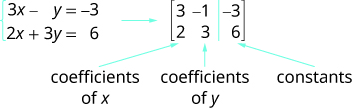
Notice the first column is made up of all the coefficients of x, the second column is the all the coefficients of y, and the third column is all the constants.
Example \(\PageIndex{1}\)
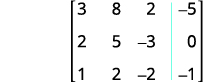
ⓐ \(\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. \) ⓑ \( \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. \)
- Answer
-
ⓐ The second equation is not in standard form. We rewrite the second equation in standard form.
\[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]
We replace the second equation with its standard form. In the augmented matrix, the first equation gives us the first row and the second equation gives us the second row. The vertical line replaces the equal signs.
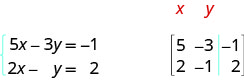
ⓑ All three equations are in standard form. In the augmented matrix the first equation gives us the first row, the second equation gives us the second row, and the third equation gives us the third row. The vertical line replaces the equal signs.
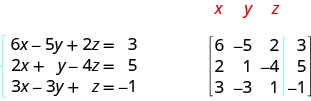
Example \(\PageIndex{2}\)
Write each system of linear equations as an augmented matrix:
ⓐ \(\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. \) ⓑ \(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)
- Answer
-
ⓐ \(\left[ \begin{array} {cc|c} 3 &8 &-3 \\ 2 &5 &−3 \end{array} \right] \)
ⓑ \(\left[ \begin{array} {ccc|c} 2 &5 &-3 &8 \\ 3 &-1 &4 &7 \\ 1 &3 &2 &−3 \end{array} \right] \)
Example \(\PageIndex{3}\)
Write each system of linear equations as an augmented matrix:
ⓐ \(\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. \) ⓑ \(\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. \)
- Answer
-
ⓐ \(\left[ \begin{array} {cc|c} 11 &9 &−5 \\ 7 &5 &−1 \end{array} \right] \)
ⓑ \(\left[ \begin{array} {ccc|c} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{array} \right] \)
It is important as we solve systems of equations using matrices to be able to go back and forth between the system and the matrix. The next example asks us to take the information in the matrix and write the system of equations.
Example \(\PageIndex{4}\)
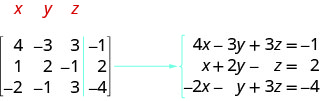
Write the system of equations that corresponds to the augmented matrix:
\(\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] \).
- Answer
-
We remember that each row corresponds to an equation and that each entry is a coefficient of a variable or the constant. The vertical line replaces the equal sign. Since this matrix is a \(4\times 3\), we know it will translate into a system of three equations with three variables.
Example \(\PageIndex{5}\)
Write the system of equations that corresponds to the augmented matrix: \(\left[ \begin{array} {ccc|c} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{array} \right] \).
- Answer
-
\(\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.\)
Example \(\PageIndex{6}\)
Write the system of equations that corresponds to the augmented matrix: \(\left[ \begin{array} {ccc|c} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{array} \right] \).
- Answer
-
\(\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.\)
Use Row Operations on a Matrix
Once a system of equations is in its augmented matrix form, we will perform operations on the rows that will lead us to the solution.
To solve by elimination, it doesn’t matter which order we place the equations in the system. Similarly, in the matrix we can interchange the rows.
When we solve by elimination, we often multiply one of the equations by a constant. Since each row represents an equation, and we can multiply each side of an equation by a constant, similarly we can multiply each entry in a row by any real number except 0.
In elimination, we often add a multiple of one row to another row. In the matrix we can replace a row with its sum with a multiple of another row.
These actions are called row operations and will help us use the matrix to solve a system of equations.
ROW OPERATIONS
In a matrix, the following operations can be performed on any row and the resulting matrix will be equivalent to the original matrix.
- Interchange any two rows.
- Multiply a row by any real number except 0.
- Add a nonzero multiple of one row to another row.
Performing these operations is easy to do but all the arithmetic can result in a mistake. If we use a system to record the row operation in each step, it is much easier to go back and check our work.
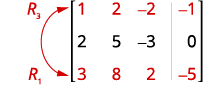
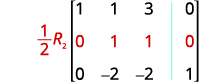
We use capital letters with subscripts to represent each row. We then show the operation to the left of the new matrix. To show interchanging a row:
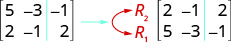
To multiply row 2 by \(−3\):
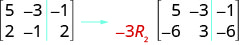
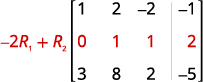
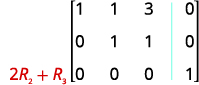
To multiply row 2 by \(−3\) and add it to row 1:
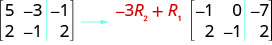
Example \(\PageIndex{7}\)
Perform the indicated operations on the augmented matrix:
ⓐ Interchange rows 2 and 3.
ⓑ Multiply row 2 by 5.
ⓒ Multiply row 3 by −2−2 and add to row 1.
\( \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] \)
- Answer
-
ⓐ We interchange rows 2 and 3.
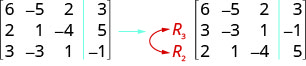
ⓑ We multiply row 2 by 5.

ⓒ We multiply row 3 by \(−2\) and add to row 1.
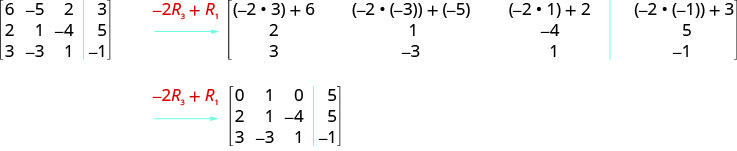
Example \(\PageIndex{8}\)
Perform the indicated operations on the augmented matrix:
ⓐ Interchange rows 1 and 3.
ⓑ Multiply row 3 by 3.
ⓒ Multiply row 1 by 2 and add to row 2.
\( \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] \)
- Answer
-
ⓐ \( \left[ \begin{array} {ccc|c} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{array} \right] \)
ⓑ \( \left[ \begin{array} {ccc|c}−2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{array} \right] \)
ⓒ \( \left[ \begin{array} {ccc|c} -2 &3 &0 &2 \\ 0 &5 &-4 &0 \\ 15 &-6 &-6 &-6 \end{array} \right] \)
Example \(\PageIndex{9}\)
Perform the indicated operations on the augmented matrix:
ⓐ Interchange rows 1 and 2,
ⓑ Multiply row 1 by 2,
ⓒ Multiply row 2 by 3 and add to row 1.
\( \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] \)
- Answer
-
ⓐ \( \left[ \begin{array} {ccc|c} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{array} \right] \)
ⓑ \( \left[ \begin{array} {ccc|c} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{array} \right] \)
ⓒ \( \left[ \begin{array} {ccc|c} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{array} \right] \)
Now that we have practiced the row operations, we will look at an augmented matrix and figure out what operation we will use to reach a goal. This is exactly what we did when we did elimination. We decided what number to multiply a row by in order that a variable would be eliminated when we added the rows together.
Given this system, what would you do to eliminate x?
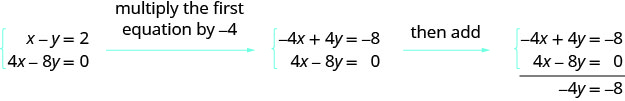
This next example essentially does the same thing, but to the matrix.
Example \(\PageIndex{10}\)
Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] \)
- Answer
-
To make the 4 a 0, we could multiply row 1 by \(−4\) and then add it to row 2.
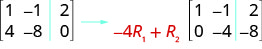
Example \(\PageIndex{11}\)
Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] \)
- Answer
-
\( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 0 &−3 &−4 \end{array} \right] \)
Example \(\PageIndex{12}\)
Perform the needed row operation that will get the first entry in row 2 to be zero in the augmented matrix: \( \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] \)
- Answer
-
\( \left[ \begin{array} {cc|c} 1 &−1 &3 \\ 0 &−5 &8 \end{array} \right] \)
Solve Systems of Equations Using Matrices
To solve a system of equations using matrices, we transform the augmented matrix into a matrix in row-echelon form using row operations. For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.
For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.
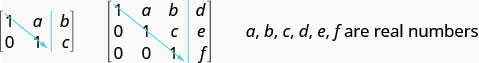
Once we get the augmented matrix into row-echelon form, we can write the equivalent system of equations and read the value of at least one variable. We then substitute this value in another equation to continue to solve for the other variables. This process is illustrated in the next example.
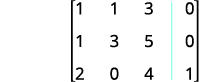
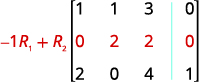
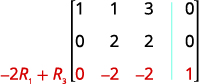
Example \(\PageIndex{14}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- Answer
-
The solution is \((4,−1)\).
Example \(\PageIndex{15}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. \)
- Answer
-
The solution is \((−2,0)\).
The steps are summarized here.
SOLVE A SYSTEM OF EQUATIONS USING MATRICES.
- Write the augmented matrix for the system of equations.
- Using row operations get the entry in row 1, column 1 to be 1.
- Using row operations, get zeros in column 1 below the 1.
- Using row operations, get the entry in row 2, column 2 to be 1.
- Continue the process until the matrix is in row-echelon form.
- Write the corresponding system of equations.
- Use substitution to find the remaining variables.
- Write the solution as an ordered pair or triple.
- Check that the solution makes the original equations true.
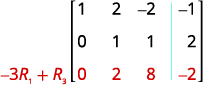
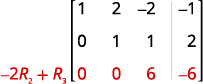
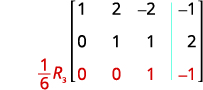
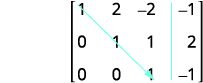
Here is a visual to show the order for getting the 1’s and 0’s in the proper position for row-echelon form.
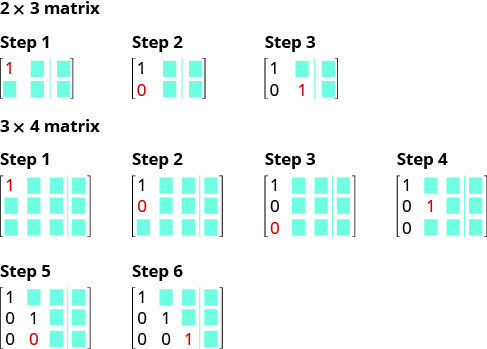
We use the same procedure when the system of equations has three equations.
Example \(\PageIndex{17}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)
- Answer
-
\((6,−1,−3)\)
Example \(\PageIndex{18}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. \)
- Answer
-
\((5,7,4)\)
So far our work with matrices has only been with systems that are consistent and independent, which means they have exactly one solution. Let’s now look at what happens when we use a matrix for a dependent or inconsistent system.
Example \(\PageIndex{20}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. \)
- Answer
-
no solution
Example \(\PageIndex{21}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. \)
- Answer
-
no solution
The last system was inconsistent and so had no solutions. The next example is dependent and has infinitely many solutions.
Example \(\PageIndex{23}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)
- Answer
-
infinitely many solutions \((x,y,z)\), where \(x=z−3;\space y=3;\space z\) is any real number.
Example \(\PageIndex{24}\)
Solve the system of equations using a matrix: \(\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)
- Answer
-
infinitely many solutions \((x,y,z)\), where \(x=5z−2;\space y=4z−3;\space z\) is any real number.
Access this online resource for additional instruction and practice with Gaussian Elimination.
Key Concepts
- Matrix: A matrix is a rectangular array of numbers arranged in rows and columns. A matrix with m rows and n columns has order \(m\times n\). The matrix on the left below has 2 rows and 3 columns and so it has order \(2\times 3\). We say it is a 2 by 3 matrix.
Each number in the matrix is called an element or entry in the matrix.
- Row Operations: In a matrix, the following operations can be performed on any row and the resulting matrix will be equivalent to the original matrix.
- Interchange any two rows
- Multiply a row by any real number except 0
- Add a nonzero multiple of one row to another row
- Row-Echelon Form: For a consistent and independent system of equations, its augmented matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.
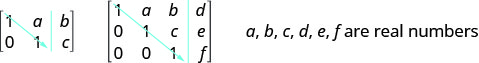
- How to solve a system of equations using matrices.
- Write the augmented matrix for the system of equations.
- Using row operations get the entry in row 1, column 1 to be 1.
- Using row operations, get zeros in column 1 below the 1.
- Using row operations, get the entry in row 2, column 2 to be 1.
- Continue the process until the matrix is in row-echelon form.
- Write the corresponding system of equations.
- Use substitution to find the remaining variables.
- Write the solution as an ordered pair or triple.
- Check that the solution makes the original equations true.
Glossary
- matrix
- A matrix is a rectangular array of numbers arranged in rows and columns.
- row-echelon form
- A matrix is in row-echelon form when to the left of the vertical line, each entry on the diagonal is a 1 and all entries below the diagonal are zeros.