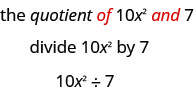1.3E: Exercises

Practice Makes Perfect

Use Variables and Algebraic Symbols

In the following exercises, translate from algebra to English.

Exercise $\PageIndex{55}$

$16−9$

Answer

$16$ minus $9$, the difference of sixteen and nine

Exercise $\PageIndex{56}$

$3\cdot 9$

Exercise $\PageIndex{57}$

$28\div 4$

Answer

$28$ divided by $4$, the quotient of twenty-eight and four

Exercise $\PageIndex{58}$

$x+11$

Exercise $\PageIndex{59}$

$(2)(7)$

Answer

$2$ times $7$, the product of two and seven

Exercise $\PageIndex{60}$

$(4)(8)$

Exercise $\PageIndex{61}$

$14<21$

Answer

fourteen is less than twenty-one

Exercise $\PageIndex{62}$

$17<35$

Exercise $\PageIndex{63}$

$36\geq 19$

Answer

thirty-six is greater than or equal to nineteen

Exercise $\PageIndex{64}$

$6n=36$

Exercise $\PageIndex{65}$

$y−1>6$

Answer

$y$ minus $1$ is greater than $6$, the difference of $y$ and one is greater than six

Exercise $\PageIndex{66}$

$y−4>8$

Exercise $\PageIndex{67}$

$2\leq 18\div 6$

Answer

$2$ is less than or equal to $18$ divided by $6$; $2$ is less than or equal to the quotient of eighteen and six

Exercise $\PageIndex{68}$

$a\neq 1\cdot12$

In the following exercises, determine if each is an expression or an equation.

Exercise $\PageIndex{69}$

$9\cdot 6=54$

Answer

equation

Exercise $\PageIndex{70}$

$7\cdot 9=63$

Exercise $\PageIndex{71}$

$5\cdot 4+3$

Answer

expression

Exercise $\PageIndex{72}$

$x+7$

Exercise $\PageIndex{73}$

$x + 9$

Answer

expression

Exercise $\PageIndex{74}$

$y−5=25$

Simplify Expressions Using the Order of Operations

In the following exercises, simplify each expression.

Exercise $\PageIndex{75}$

$5^{3}$

Answer

$125$

Exercise $\PageIndex{76}$

$8^{3}$

Exercise $\PageIndex{77}$

$2^{8}$

Answer

$256$

Exercise $\PageIndex{78}$

$10^{5}$

In the following exercises, simplify using the order of operations.

Exercise $\PageIndex{79}$

1. $3+8\cdot 5$
2. $(3+8)\cdot 5$

Answer

1. $43$
2. $55$

Exercise $\PageIndex{80}$

1. $2+6\cdot 3$
2. $(2+6)\cdot 3$

Exercise $\PageIndex{81}$

$2^{3}−12\div (9−5)$

Answer

$5$

Exercise $\PageIndex{82}$

$3^{2}−18\div(11−5)$

Exercise $\PageIndex{83}$

$3\cdot 8+5\cdot 2$

Answer

$34$

Exercise $\PageIndex{84}$

$4\cdot 7+3\cdot 5$

Exercise $\PageIndex{85}$

$2+8(6+1)$

Answer

$58$

Exercise $\PageIndex{86}$

$4+6(3+6)$

Exercise $\PageIndex{87}$

$4\cdot 12/8$

Answer

$6$

Exercise $\PageIndex{88}$

$2\cdot 36/6$

Exercise $\PageIndex{89}$

$(6+10)\div(2+2)$

Answer

$4$

Exercise $\PageIndex{90}$

$(9+12)\div(3+4)$

Exercise $\PageIndex{91}$

$20\div4+6\cdot5$

Answer

$35$

Exercise $\PageIndex{92}$

$33\div3+8\cdot2$

Exercise $\PageIndex{93}$

$3^{2}+7^{2}$

Answer

$58$

Exercise $\PageIndex{94}$

$(3+7)^{2}$

Exercise $\PageIndex{95}$

$3(1+9\cdot6)−4^{2}$

Answer

$149$

Exercise $\PageIndex{96}$

$5(2+8\cdot4)−7^{2}$

Exercise $\PageIndex{97}$

$2[1+3(10−2)]$

Answer

$50$

Exercise $\PageIndex{98}$

$5[2+4(3−2)]$

Evaluate an Expression

In the following exercises, evaluate the following expressions.

Exercise $\PageIndex{99}$

$7x+8$ when $x=2$

Answer

$22$

Exercise $\PageIndex{100}$

$8x−6$ when $x=7$

Exercise $\PageIndex{101}$

$x^{2}$ when $x = 12$

Answer

$144$

Exercise $\PageIndex{102}$

$x^{3}$ when $x = 5$

Exercise $\PageIndex{103}$

$x^{5}$ when $x = 2$

Answer

$32$

Exercise $\PageIndex{104}$

$4^{x}$ when $x = 2$

Exercise $\PageIndex{105}$

$x^{2}+3x−7$ when $x = 4$

Answer

$21$

Exercise $\PageIndex{106}$

$6x + 3y - 9$ when $x = 10, y = 7$

Answer

$9$

Exercise $\PageIndex{107}$

$(x + y)^{2}$ when $x = 6, y = 9$

Exercise $\PageIndex{108}$

$a^{2} + b^{2}$ when $a = 3, b = 8$

Answer

$73$

Exercise $\PageIndex{109}$

$r^{2} - s^{2}$ when $r = 12, s = 5$

Exercise $\PageIndex{110}$

$2l + 2w$ when $l = 15, w = 12$

Answer

$54$

Exercise $\PageIndex{111}$

$2l + 2w$ when $l = 18, w = 14$

Simplify Expressions by Combining Like Terms

In the following exercises, identify the coefficient of each term.

Exercise $\PageIndex{112}$

$8a$

Answer

$8$

Exercise $\PageIndex{113}$

$13m$

Exercise $\PageIndex{114}$

$5r^{2}$

Answer

$5$

Exercise $\PageIndex{115}$

$6x^{3}$

In the following exercises, identify the like terms.

Exercise $\PageIndex{116}$

$x^{3}, 8x, 14, 8y, 5, 8x^{3}$

Answer

$x^{3}$ and $8x^{3}$, $14$ and $5$

Exercise $\PageIndex{117}$

$6z, 3w^{2}, 1, 6z^{2}, 4z, w^{2}$

Exercise $\PageIndex{118}$

$9a, a^{2}, 16, 16b^{2}, 4, 9b^{2}$

Answer

$16$ and $4$, $16b^{2}$ and $9b^{2}$

Exercise $\PageIndex{119}$

$3, 25r^{2}, 10s, 10r, 4r^{2}, 3s$

In the following exercises, identify the terms in each expression.

Exercise $\PageIndex{120}$

$15x^{2} + 6x + 2$

Answer

$15x^{2}, 6x, 2$

Exercise $\PageIndex{121}$

$11x^{2} + 8x + 5$

Exercise $\PageIndex{122}$

$10y^{3} + y + 2$

Answer

$10y^{3}, y, 2$

Exercise $\PageIndex{123}$

$9y^{3} + y + 5$

In the following exercises, simplify the following expressions by combining like terms.

Exercise $\PageIndex{124}$

$10x+3x$

Answer

$13x$

Exercise $\PageIndex{125}$

$15x+4x$

Exercise $\PageIndex{126}$

$4c + 2c + c$

Answer

$7c$

Exercise $\PageIndex{127}$

$6y + 4y + y$

Exercise $\PageIndex{128}$

$7u + 2 + 3u + 1$

Answer

$10u + 3$

Exercise $\PageIndex{129}$

$8d + 6 + 2d + 5$

Exercise $\PageIndex{130}$

$10a + 7 + 5a - 2 + 7a - 4$

Answer

$22a + 1$

Exercise $\PageIndex{131}$

$7c + 4 + 6c - 3 + 9c - 1$

Exercise $\PageIndex{132}$

$3x^{2} + 12x + 11 + 14x^{2} + 8x + 5$

Answer

$17x^{2} + 20x + 16$

Exercise $\PageIndex{133}$

$5b^{2} + 9b + 10 + 2b^{2} + 3b - 4$

Translate an English Phrase to an Algebraic Expression

In the following exercises, translate the phrases into algebraic expressions.

Exercise $\PageIndex{134}$

the difference of $14$ and $9$

Answer

$14−9$

Exercise $\PageIndex{135}$

the difference of $19$ and $8$

Exercise $\PageIndex{136}$

the product of $9$ and $7$

Answer

$9\cdot 7$

Exercise $\PageIndex{137}$

the product of $8$ and $7$

Exercise $\PageIndex{138}$

the quotient of $36$ and $9$

Answer

$36\div 9$

Exercise $\PageIndex{139}$

the quotient of $42$ and $7$

Exercise $\PageIndex{140}$

the sum of $8x$ and $3x$

Answer

$8x+3x$

Exercise $\PageIndex{141}$

the sum of $13x$ and $3x$

Exercise $\PageIndex{142}$

the quotient of $y$ and $3$

Answer

$\frac{y}{3}$

Exercise $\PageIndex{143}$

the quotient of $y$ and $8$

Exercise $\PageIndex{144}$

eight times the difference of $y$ and nine

Answer

$8(y−9)$

Exercise $\PageIndex{145}$

seven times the difference of $y$ and one

Exercise $\PageIndex{146}$

Eric has rock and classical CDs in his car. The number of rock CDs is $3$ more than the number of classical CDs. Let $c$ represent the number of classical CDs. Write an expression for the number of rock CDs.

Answer

$c+3$

Exercise $\PageIndex{147}$

The number of girls in a second-grade class is $4$ less than the number of boys. Let $b$ represent the number of boys. Write an expression for the number of girls.

Exercise $\PageIndex{148}$

Greg has nickels and pennies in his pocket. The number of pennies is seven less than twice the number of nickels. Let $n$ represent the number of nickels. Write an expression for the number of pennies.

Answer

$2n - 7$

Exercise $\PageIndex{149}$

Jeannette has $5 and $10 bills in her wallet. The number of fives is three more than six times the number of tens. Let $t$ represent the number of tens. Write an expression for the number of fives.

Everyday Math

Exercise $\PageIndex{150}$

Car insurance Justin’s car insurance has a $750 deductible per incident. This means that he pays $750 and his insurance company will pay all costs beyond $750. If Justin files a claim for $2,100.

1. how much will he pay?
2. how much will his insurance company pay?

Answer

1. $750
2. $1,350

Exercise $\PageIndex{151}$

Home insurance Armando’s home insurance has a $2,500 deductible per incident. This means that he pays $2,500 and the insurance company will pay all costs beyond $2,500. If Armando files a claim for $19,400.

1. how much will he pay?
2. how much will the insurance company pay?

Writing Exercises

Exercise $\PageIndex{152}$

Explain the difference between an expression and an equation.

Answer

Answers may vary

Exercise $\PageIndex{153}$

Why is it important to use the order of operations to simplify an expression?

Exercise $\PageIndex{154}$

Explain how you identify the like terms in the expression $8a^{2} + 4a + 9 - a^{2} - 1$

Answer

Answers may vary

Exercise $\PageIndex{155}$

Explain the difference between the phrases “$4$ times the sum of $x$ and $y$” and “the sum of $4$ times $x$ and $y$.”

Self Check

ⓐ Use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

More Exponent Practice

Exercise $\PageIndex{156}$

compute the exact value of the given exponential expression

1. 0^1 2. 1^3 3. 3^2 4. 3^4

5. 4^1 6. 5^2 7. 4^3 8. 4^2

9. −3^2 10. −3^3 11. −4^2 12. −2^4

13. (−5)^2 14. (−2)^4 15. (−3)^3 16. (−2)^5

17. (−6)^2 18. (−4)^2 19. (−5)^3 20. (−4)^3

21. −(−5)^2 22. −(−3)^4 23. −(−4)^3 24. −(−2)^5

Answers to odd problems for E.156

1. 0 3. 9

5. 4 7. 64

9. −9 11. −64

13. 25 15. −27

17. 36 19. −125

21. −25 23. 64

 

More Order of Operations Practice

Exercise $\PageIndex{157}$

Compute the exact value of the given expression.

1. 9 − 1(−7) 2. 85 − 8(9) 3. 3 + 9(4) 4. 6 + 7(−1) 5. −2 − 3(−5) 6. 64 − 7(7)

7. 10 + 12(−5) 8. 4 + 12(4) 9. 30 · 5 ÷ 3 10. 72 · 6÷ 4 11. 32 ÷ 4 · 4 12. 64 ÷ 4 · 4

13. 15 ÷ 1 · 3 14. 18 ÷ 6 · 1 15. 40 ÷ 5 · 4 16. 30 ÷ 6 · 5

19. 10 − 72 ÷ 6 · 3+8 20. 8 − 120 ÷ 5 · 6+7 21. 3 − 24 ÷ 4 · 3+4 22. 4 − 40 ÷ 5 · 4+9 23. 2+6 ÷ 1 · 6 − 1 24. 1 + 12 ÷ 2 · 2 − 6

Answers to odd problems for E.157 

1. 16 3. 39 5. 13

7. −50 9. 50 11. 32

13. 45 15. −216

19. −18 21. −11 23. 37

 

More Practice Changing English Expressions into Algebraic Expressions

Exercise $\PageIndex{158}$

Translate the following phrases into algebraic expressions.

1.    a. the difference of $5x^2$ and $6xy$          b. the quotient of $6y^2$ and $5x$          c. Twenty-one more than $y^2$          d. $6x$ less than $81x^2$ 2.    a. the difference of $17x^2$ and $17x^2$ and $5xy$          b. the quotient of $8y^3$ and $3x$          c. Eighteen more than $a^2$;          d. $11b$ less than $100b^2$

3.    a. the sum of $4ab^2$ and $3a^2b$          b. the product of $4y^2$ and $5x$          c. Fifteen more than $m$          d. $9x$ less than $121x^2$ 4.    a. the sum of $3x^2y$ and $7xy^2$          b. The product of $6xy^2$ and $4z$          c. Twelve more than $3x^2$          d. $7x^2$ less than $63x^3$

Answers to odd problems for E.158 #1-4

1a. $5x^2−6xy$      b. $\frac{6y^2}{5x}$      c. $y^2+21$      d. $81x^2−6x$          3a. $4ab^2+3a^2b$      b. $20xy^2$      c. $m+15$      d. $121x^2−9x$.

Translate the following phrases into algebraic expressions.

5.    a. four times the difference of $y$ and six          b. the difference of four times $y$ and $6$ 6.    a. five times the difference of $y$ and two           b. the difference of five times $y$ and $2$

7.    a. five times the sum of $3x$ and $y$          b. the sum of five times $3x$ and $y$ 8.    a. eleven times the sum of $4x^2$ and $5x$          b. the sum of eleven times $4x^2$ and $5x$

Answers to odd problems for E.158 #5-8

5 a. $4(y−6)$      b. $4y−6$                  7 a. $5(3x+y)$      b. $5(3x)+y$.

 

Translate the following phrases into algebraic expressions.

9. The length of a rectangle is $5$ inches less than the width. Let $w$ represent the width of the rectangle. Write an expression for the length of the rectangle.

10. The width of a rectangle is $2$ meters greater than the length. Let $L$  represent the length of the rectangle. Write an expression for the width of the rectangle

11. A collection contains jazz and classical CDs. The number of jazz CDs is $3$ more than the number of classical CDs. Let $c$ represent the number of classical CDs. Write an expression for the number of jazz CDs.

12. The number of girls in a second-grade class is $4$ less than the number of boys. Let $b$ represent the number of boys. Write an expression for the number of girls.

13. A playlist contains rock and country songs. The number of rock songs is 14 more than twice the number of country songs. Let $c$ represent the number of country songs. Write an expression for the number of rock songs.

14. The number of women in a Statistics class is $8$ less than twice the number of men. Let $m$ represent the number of men. Write an expression for the number of women.

15. Greg has nickels and pennies in his pocket. The number of pennies is seven less than three times the number of nickels. Let $n$ represent the number of nickels. Write an expression for the number of pennies.

16. Greg has nickels and pennies in his pocket. The number of pennies is four more than twice the number of nickels. Let $n$ represent the number of nickels. Write an expression for the number of pennies.

Answers to odd problems for E.158 #9-16

9.  $w-5$     11. $c+3$     13. $2c+14$    15.  $3n-7$ .