2.8E: Exercises for Section 2.8

Last updated
Save as PDF

Page ID: 57739

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In Exercises 1 - 8, use both interval and set-builder notation to describe the intersection of the two intervals shown on the graph. Also, sketch the graph of the intersection on the real number line.

Exercise 1

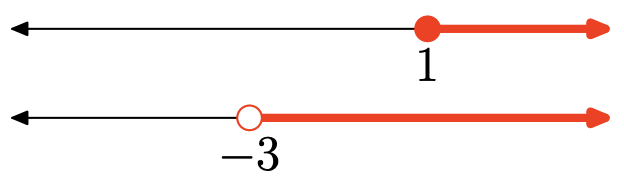
$Screen Shot 2019-07-29 at 10.25.01 PM.png$

Answer

The intersection is the set of points that are in both intervals (shaded on both graphs). Graph of the intersection:

$Screen Shot 2019-08-05 at 10.52.32 AM.png$

Set-Builder Notation: $\{x \, | \, x \geq 1\}$

Interval Notation: $[1, \infty)$

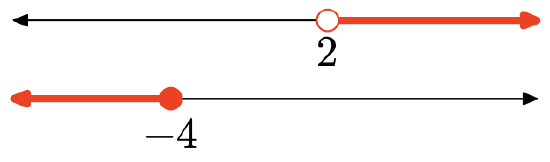
Exercise 2

$Screen Shot 2019-07-29 at 10.26.55 PM.png$

Exercise 3

$Screen Shot 2019-07-29 at 10.27.31 PM.png$

Answer

There are no points that are in both intervals (shaded in both), so there is no intersection. Graph of the intersection:

$Screen Shot 2019-08-05 at 10.53.41 AM.png$

no intersection

Set-Builder Notation: $ \{ \; \} $

Interval Notation: none

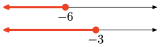
Exercise 4

$Screen Shot 2019-07-29 at 10.28.18 PM.png$

Exercise 5

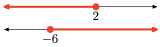
$Screen Shot 2019-07-29 at 10.29.22 PM.png$

Answer

The intersection is the set of points that are in both intervals (shaded in both). Graph of the intersection:

$Screen Shot 2019-08-05 at 10.54.24 AM.png$

Set-Builder Notation: $\{x \, | \, -6 \leq x \leq 2\}$

Interval Notation: $[-6,2]$

Exercise 6

$Screen Shot 2019-07-29 at 10.30.25 PM.png$

Exercise 7

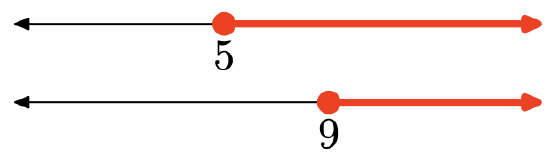
$Screen Shot 2019-07-29 at 10.31.23 PM.png$

Answer

The intersection is the set of points that are in both intervals (shaded in both). Graph of the intersection:

$Screen Shot 2019-08-05 at 10.55.19 AM.png$

Set-Builder Notation: $\{x \, | \, x \geq 9\}$

Interval Notation: $[9, \infty)$

Exercise 8

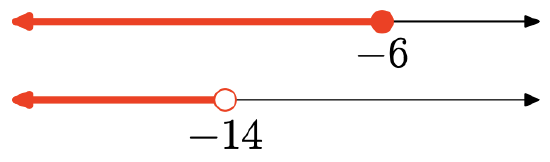
$Screen Shot 2019-07-29 at 10.33.57 PM.png$

In Exercises 9 - 16, use both interval notation and set-builder notation to describe the union of the two intervals shown on the graph. Also, sketch the graph of the union on the real number line.

Exercise 9

$Screen Shot 2019-07-29 at 10.37.45 PM.png$

Answer

The union is the set of all points that are in one interval or the other (shaded in either graph). Graph of the union:

$Screen Shot 2019-08-05 at 10.58.47 AM.png$

Set-Builder Notation: $\{x \, | \, x \leq-8\}$

Interval Notation: $(-\infty,-8]$

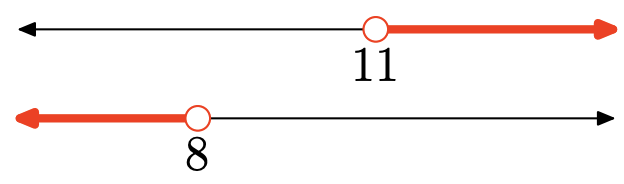
Exercise 10

$Screen Shot 2019-07-29 at 10.39.08 PM.png$

Exercise 11

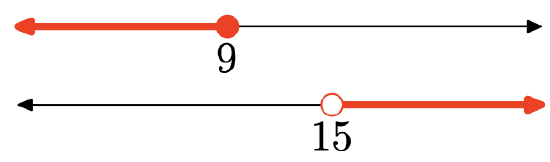
$Screen Shot 2019-07-29 at 10.39.38 PM.png$

Answer

The union is the set of all points that are in one interval or the other (shaded in either graph). Graph of the union:

$Screen Shot 2019-08-05 at 11.01.44 AM.png$

Set-Builder Notation: $\{x \, | \, x \leq 9 \text { or } x>15\}$

Interval Notation: $(-\infty, 9] \cup(15, \infty)$

Exercise 12

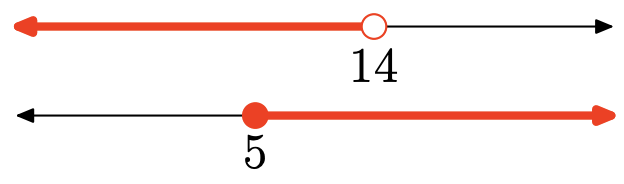
$Screen Shot 2019-07-29 at 10.40.55 PM.png$

Exercise 13

$Screen Shot 2019-07-29 at 10.42.41 PM.png$

Answer

The union is the set of all points that are in one interval or the other (shaded in either). Graph of the union:

$Screen Shot 2019-08-05 at 11.03.02 AM.png$

Set-Builder Notation: $\{x \, | \, x<3\}$

Interval Notation: $(-\infty, 3)$

Exercise 14

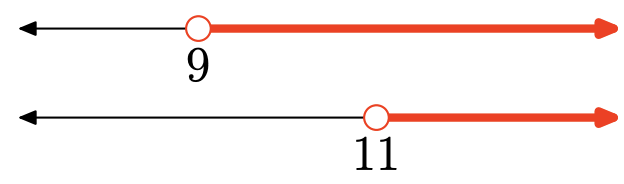
$Screen Shot 2019-07-29 at 10.44.52 PM.png$

Exercise 15

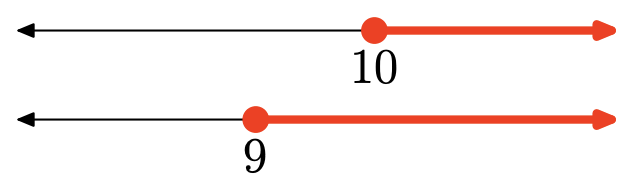
$Screen Shot 2019-07-29 at 10.45.57 PM.png$

Answer

The union is the set of all points that are in one interval or the other (shaded in either). Graph of the union:

$Screen Shot 2019-08-05 at 11.04.38 AM.png$

Set-Builder Notation: $\{x \, | \, x \geq 9\}$

Interval Notation: $[9, \infty)$

Exercise 16

$Screen Shot 2019-07-29 at 10.46.54 PM.png$

In Exercises 17 - 32, use interval notation to describe the given set. Also, sketch the graph of the set on the real number line.

Exercise 17

$\{x \, | \, x \geq-6 \text { and } x>-5\}$

Answer

This set is the same as $\{x \, | \, x>-5\}$, which is $(-5, \infty)$ in interval notation. Graph of the set:

$Screen Shot 2019-08-05 at 11.06.12 AM.png$

Exercise 18

$\{x \, | \, x \leq 6 \text { and } x \geq 4\}$

Exercise 19

$\{x \, | \, x \geq-1 \text { or } x<3\}$

Answer

Every real number is in one or the other of the two intervals. Therefore, the set is the set of all real numbers $(-\infty, \infty)$. Graph of the set:

$Screen Shot 2019-08-05 at 11.07.04 AM.png$

Exercise 20

$\{x \, | \, x>-7 \text { and } x>-4\}$

Exercise 21

$\{x \, | \, x \geq -1 \text { or } x>6\}$

Answer

This set is the same as $\{x \, | \, x \geq-1\}$, which is $[-1, \infty)$ in interval notation. Graph of the set:

$Screen Shot 2019-08-05 at 11.10.10 AM.png$

Exercise 22

$\{x \, | \, x \geq 7 \text { or } x<-2\}$

Exercise 23

$\{x \, | \, x \geq 6 \text { or } x>-3\}$

Answer

This set is the same as $\{x \, | \, x>-3\}$, which is $(-3, \infty)$ in interval notation. Graph of the set:

$Screen Shot 2019-08-05 at 11.12.01 AM.png$

Exercise 24

$\{x \, | \, x \leq 1 \text { or } x>0\}$

Exercise 25

$\{x \, | \, x<2 \text { and } x<-7\}$

Answer

This set is the same as $\{x \, | \, x<-7\}$, which is $(-\infty,-7)$ in interval notation. Graph of the set:

$Screen Shot 2019-08-05 at 11.13.07 AM.png$

Exercise 26

$\{x \, | \, x \leq-3 \text { and } x<-5\}$

Exercise 27

$\{x \, | \, x \leq-3 \text { or } x \geq 4\}$

Answer

This set is the union of two intervals, $(-\infty,-3] \cup[4, \infty)$. Graph of the set:

$Screen Shot 2019-08-05 at 11.14.04 AM.png$

Exercise 28

$\{x \, | \, x<11 \text { or } x \leq 8\}$

Exercise 29

$\{x \, | \, x \geq 5 \text { and } x \leq 1\}$

Answer

There are no numbers that satisfy both inequalities. Thus, there is no intersection. Graph of the set:

$Screen Shot 2019-08-05 at 11.14.56 AM.png$

Exercise 30

$\{x \, | \, x<5 \text { or } x<10\}$

Exercise 31

$\{x \, | \, x \leq 5 \text { and } x \geq-1\}$

Answer

This set is the same as $\{x \, | \, -1 \leq x \leq 5\}$, which is [−1, 5] in interval notation. Graph of the set

$Screen Shot 2019-08-05 at 11.17.54 AM.png$

Exercise 32

$\{x \, | \, x>-3 \text { and } x<-6\}$

In Exercises 33 - 44, solve the inequality. Express your answer in both interval and set-builder notations, and graph the solution on a number line. Answers include worked out solutions.

Exercise 33

$-8 x-3 \leq-16 x-1$

Answer

\[\begin{aligned} & -8 x-3 \leq-16 x-1 \\ \Longrightarrow \quad & − 8x + 16x \leq −1 + 3 \\ \Longrightarrow \quad& 8x \leq 2 \\ \Longrightarrow \quad & x \leq \frac{1}{4}\end{aligned}\]

Thus, the solution interval is

$Screen Shot 2019-08-07 at 10.21.02 PM.png$

Set-Builder Notation: $\{x \, | \, x \leq \frac{1}{4}\}$

Interval Notation: $(−\infty, \frac{1}{4}]$

Exercise 34

$6 x-6>3 x+3$

Exercise 35

$-12 x+5 \leq-3 x-4$

Answer

\[\begin{aligned} & -12 x+5 \leq-3 x-4 \\ \Longrightarrow \quad & -12x + 3x \leq −4 − 5 \\ \Longrightarrow \quad& -9x \leq -9 \\ \Longrightarrow \quad & x \geq 1\end{aligned}\]

Thus, the solution interval is

$Screen Shot 2019-08-08 at 10.56.57 PM.png$

Set-Builder Notation: $\\{x \, | \, x\geq 1\}$

Interval Notation: $[1,\infty)$

Exercise 36

$7 x+3 \leq-2 x-8$

Exercise 37

$-11 x-9<-3 x+1$

Answer

\[\begin{aligned} & − 11x − 9 < −3x + 1 \\ \Longrightarrow \quad & − 11x + 3x < 1 + 9 \\ \Longrightarrow \quad& − 8x < 10 \\ \Longrightarrow \quad & x > -\frac{5}{4}\end{aligned}\]

Thus, the solution interval is

$Screen Shot 2019-08-08 at 11.00.01 PM.png$

Set-Builder Notation: $\{x \, | \, x >−\frac{5}{4} \}$

Interval Notation: $(−\frac{5}{4} ,\infty) $

Exercise 38

$4 x-8 \geq-4 x-5$

Exercise 39

$4 x-5>5 x-7$

Answer

\[\begin{align*} & 4x − 5 > 5x − 7\\ \Longrightarrow \quad & 4x − 5x > −7 + 5 \\ \Longrightarrow \quad& − x > −2 \\ \Longrightarrow \quad &x < 2\end{align*}\]
Thus, the solution interval is

$Screen Shot 2019-08-08 at 11.02.23 PM.png$

Set-Builder Notation: $\{x \, | \, x < 2\}$

Interval Notation: $(−\infty, 2) $

Exercise 40

$-14 x+4>-6 x+8$

Exercise 41

$2 x-1>7 x+2$

Answer

\[\begin{aligned} & 2x − 1 > 7x + 2\\ \Longrightarrow \quad & 2x − 7x > 2 + 1 \\ \Longrightarrow \quad& − 5x > 3 \\ \Longrightarrow \quad &x < −\frac{3}{5}\end{aligned}\]
Thus, the solution interval is

$Screen Shot 2019-08-08 at 11.04.53 PM.png$

Set-Builder Notation: $\{x \, | \, x < −\frac{3}{5}\}$

Interval Notation: $(−\infty, −\frac{3}{5})$

Exercise 42

$-3 x-2>-4 x-9$

Exercise 43

$-3 x+3<-11 x-3$

Answer

\[\begin{aligned} & − 3x + 3 < −11x − 3\\ \Longrightarrow \quad & − 3x + 11x < −3 − 3 \\ \Longrightarrow \quad& 8x < −6 \\ \Longrightarrow \quad &x < -\frac{3}{4}\end{aligned}\]
Thus, the solution interval is

$Screen Shot 2019-08-08 at 11.07.23 PM.png$

Set-Builder Notation: $\{x \, | \, x < −\frac{3}{4}\}$

Interval Notation: $(−\infty, −\frac{3}{4})$

Exercise 44

$6 x+3<8 x+8$

In Exercises 45-53, solve the compound inequality. Express your answer in both interval and set-builder notations, and graph the solution on a number line. Worked out solutions are provided in the Answers for #45 and #47. Only the interval notation version of the answer is given for Answers in #49-82.

Exercise 45

$2 x-1<4$ or $7 x+1 \geq-4$

Answer

\[\begin{aligned} & 2x − 1 < 4 \text{ or } 7x + 1 \geq −4\\ \Longrightarrow \quad & 2x < 5\quad \text{or}\quad 7x \geq −5 \\ \Longrightarrow \quad&x<\frac{5}{2}\quad\text{or}\quad x\geq-\frac{5}{7}\end{aligned}\]

$Screen Shot 2019-08-08 at 11.11.56 PM.png$

For the union, shade anything shaded in either graph. The solution is the set of all real numbers. $(−\infty,\infty)$.

$Screen Shot 2019-08-08 at 11.13.59 PM.png$

Set-Builder Notation: $\{x \, | \, x \in \mathbb{R}\}$

Interval Notation: $(−\infty, \infty)$

Exercise 46

$-8 x+9<-3$ and $-7 x+1>3$

Exercise 47

$-6 x-4<-4$ and $-3 x+7 \geq-5$

Answer

\[\begin{aligned} & − 6x − 4 < −4 \text{ and } − 3x + 7 \geq −5\\ \Longrightarrow \quad & -6x < 0\quad \text{and}\quad -3x \geq −12 \\ \Longrightarrow \quad&x>0\quad\text{and}\quad x\leq4 \\ \Longrightarrow \quad & 0< x \leq 4 \end{aligned}\]

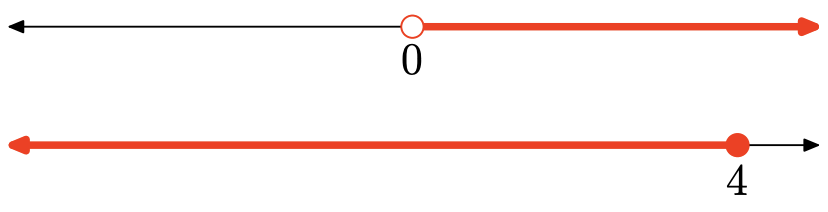
$Screen Shot 2019-08-08 at 11.21.51 PM.png$

The intersection is all points shaded in both graphs, so the solution is

$Screen Shot 2019-08-08 at 11.23.30 PM.png$

Set-Builder Notation: $\{x \, | \, 0 < x \leq 4\}$

Interval Notation: $(0, 4]$

Exercise 48

$-3 x+3 \leq 8$ and $-3 x-6>-6$

Exercise 49

$8 x+5 \leq-1$ and $4 x-2>-1$

Answer: No Solution
Set-Builder Notation: $ \{ \; \} $

Exercise 50

$-x-1<7$ and $-6 x-9 \geq 8$

Exercise 51

$-3 x+8 \leq-5$ or $-2 x-4 \geq-3$

Answer: No Solution
Set-Builder Notation: $ \{ \; \} $

Exercise 52

$-6 x-7<-3$ and $-8 x \geq 3$

Exercise 53

$9 x-9 \leq 9$ and $5 x>-1$

Answer: Interval Notation: $ \left( -\dfrac{1}{5}, 2 \right] $

Exercise $\PageIndex{54}$

$-7 x+3<-3$ or $-8 x \geq 2$

Exercise $\PageIndex{55}$

$3 x-5<4$ and $-x+9>3$

Answer: Interval Notation: $(−\infty, 3) $

Exercise $\PageIndex{56}$

$-8 x-6<5$ or $4 x-1 \geq 3$

Exercise $\PageIndex{57}$

$9 x+3 \leq-5$ or $-2 x-4 \geq 9$

Answer: Interval Notation: $ \left(−\infty, -\dfrac{8}{9} \right) $

Exercise $\PageIndex{58}$

$-7 x+6<-4$ or $-7 x-5>7$

Exercise $\PageIndex{59}$

$4 x-2 \leq 2$ or $3 x-9 \geq 3$

Answer: Add texts here. $ (-\infty,1] \cup [4, \infty) $

Exercise $\PageIndex{60}$

$-5 x+5<-4$ or $-5 x-5 \geq-5$

Exercise $\PageIndex{61}$

$5 x+1<-6$ and $3 x+9>-4$

Answer: Interval Notation: $ \left( -\dfrac{13}{3}, -\dfrac{7}{5} \right) $

Exercise $\PageIndex{62}$

$7 x+2<-5$ or $6 x-9 \geq-7$

Exercise $\PageIndex{63}$

$-7 x-7<-2$ and $3 x \geq 3$

Answer: Interval Notation: $ [ 1, \infty) $

Exercise $\PageIndex{64}$

$4 x+1<0$ or $8 x+6>9$

Exercise $\PageIndex{65}$

$7 x+8<-3$ and $8 x+3 \geq-9$

Answer: No Solution
Set-Builder Notation: $ \{ \; \} $

Exercise $\PageIndex{66}$

$3 x<2$ and $-7 x-8 \geq 3$

Exercise $\PageIndex{67}$

$-5 x+2 \leq-2$ and $-6 x+2 \geq 3$

Answer: No Solution
Set-Builder Notation: $ \{ \; \} $

Exercise $\PageIndex{68}$

$4 x-1 \leq 8$ or $3 x-9>0$

Exercise $\PageIndex{69}$

$2 x-5 \leq 1$ and $4 x+7>7$

Answer: $ (0, 3] $

Exercise $\PageIndex{70}$

$3 x+1<0$ or $5 x+5>-8$

Exercise $\PageIndex{71}$

$-8 x+7 \leq 9$ or $-5 x+6>-2$

Answer: $(−\infty, \infty) $

Exercise $\PageIndex{72}$

$x-6 \leq-5$ and $6 x-2>-3$

Exercise $\PageIndex{73}$

$-4 x-8<4$ or $-4 x+2>3$

Answer: $(−\infty, \infty) $

Exercise $\PageIndex{74}$

$9 x-5<2$ or $-8 x-5 \geq-6$

Exercise $\PageIndex{75}$

$-9 x-5 \leq-3$ or $x+1>3$

Answer: $ \left(-\dfrac{2}{9}, \infty \right) $

Exercise $\PageIndex{76}$

$-5 x-3 \leq 6$ and $2 x-1 \geq 6$

Exercise $\PageIndex{77}$

$-1 \leq-7 x-3 \leq 2$

Answer: Interval Notation: $ \left[ -\dfrac{5}{7}, -\dfrac{2}{7} \right] $

Exercise $\PageIndex{78}$

$0<5 x-5<9$

Exercise 79

$5<9 x-3 \leq 6$

Answer

Graph of the solution: $MTH098 Section 2.8E #79.png$

Set-Builder Notation: $\{x \, | \, \frac{8}{9} \lt x \leq 1\}$

Interval Notation: $ (\frac{8}{9},1] $

Exercise $\PageIndex{80}$

$-6<7 x+3 \leq 2$

Exercise $\PageIndex{81}$

$-2<-7 x+6<6$

Answer: Interval Notation: $ \left( 0, \dfrac{8}{7} \right) $

Exercise 82

$-9<-2 x+5 \leq 1$

In Exercises 83-94, solve the given inequality for x. Graph the solution set on a number line, then use interval and setbuilder notation to describe the solution set. Only the interval notation version of the answer is given for Answers in #83-94.

Exercise $\PageIndex{83}$

$-\frac{1}{3}<\frac{x}{2}+\frac{1}{4}<\frac{1}{3}$

Answer: Interval Notation: $ \left( -\dfrac{7}{6}, \dfrac{1}{6} \right) $

Exercise $\PageIndex{84}$

$-\frac{1}{5}<\frac{x}{2}-\frac{1}{4}<\frac{1}{5}$

Exercise $\PageIndex{85}$

$-\frac{1}{2}<\frac{1}{3}-\frac{x}{2}<\frac{1}{2}$

Answer: Interval Notation: $ \left( -\dfrac{1}{3}, \dfrac{5}{3} \right) $

Exercise 86

$-\frac{2}{3} \leq \frac{1}{2}-\frac{x}{5} \leq \frac{2}{3}$

Exercise $\PageIndex{87}$

$-1<x-\frac{x+1}{5}<2$

Answer: Interval Notation: $ \left( -1, \dfrac{11}{4} \right) $

Exercise $\PageIndex{88}$

$-2<x-\frac{2 x-1}{3}<4$

Exercise $\PageIndex{89}$

$-2<\frac{x+1}{2}-\frac{x+1}{3} \leq 2$

Answer: Interval Notation: $ \left( -13, 11 \right] $

Exercise $\PageIndex{90}$

$-3<\frac{x-1}{3}-\frac{2 x-1}{5} \leq 2$

Exercise $\PageIndex{91}$

$x<4-x<5$

Answer: Interval Notation: $ \left( -1, 2 \right) $

Exercise $\PageIndex{92}$

$-x<2 x+3 \leq 7$

Exercise $\PageIndex{93}$

$-x<x+5 \leq 11$

Answer: Interval Notation: $ \left( -\dfrac{5}{2}, 6 \right] $

Exercise $\PageIndex{94}$

$−2x < 3 − x \leq 8$

More Practice with Compound Inequalities

Exercise $\PageIndex{95}$

For each graph below, describe the interval (a) using set-builder notation and (b) using interval notation.

1.
$WeChatb5d2ec2c0d59c1eea3469a07a6e3eeb3.png$

2.
$Screen Shot 2019-08-05 at 10.49.22 AM.png$

3.
$Screen Shot 2019-08-05 at 10.50.50 AM.png$

4.
$Screen Shot 2019-08-05 at 10.54.24 AM.png$

5.
$Screen Shot 2019-08-05 at 11.17.54 AM.png$

6.
$Screen Shot 2019-08-08 at 11.23.30 PM.png$

7.
$WeChata8b836e07fe50d89bd7fc775102533f2.png$ x

8.
$WeChat4bb84b27707520b9ef125fb6f5e8b38a.png$

Answer

1. (a) $\{x| \, 3 \leq x \leq 4\}$ (b) $[3,4]$
3. (a) $\{x| -4 \lt x \lt 1\}$ (b) $(-4,1)$

5. (a) $\{x| -1 \leq x \leq 5\}$ (b) $[-1,5]$
7. (a) $\{x| -1 \lt x \leq 5\}$ (b) $(-1,5]$

Search

Exercise \(\PageIndex{95}\)