2.7E: Exercises for Section 2.7
( \newcommand{\kernel}{\mathrm{null}\,}\)
1) Draw a number line, then plot the numbers 4,3,−4,7/8, and −8/3 on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.
- Answer
-
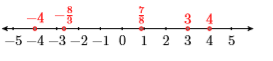
2) Draw a number line, then plot the numbers 5,3,−4,5/7, and −4/3 on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.
3) Draw a number line, then plot the numbers −5,5,4,2/3, and 8/3 on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.
- Answer
-
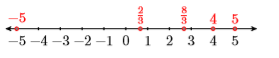
4) Draw a number line, then plot the numbers −3,−2,4,1/3, and 5/2 on your number line. Label each point with its value. Finally, list the numbers in order, from smallest to largest.
In Exercises 5-20, shade each of the following sets on a number line.
5) {x|x≥−7}
- Answer
-
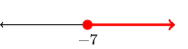
6) {x|x≥−1}
7) {x|x<2}
- Answer
-
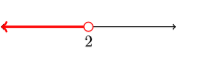
8) {x|x<−6}
9) (−∞,2)
- Answer
-
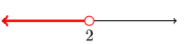
10) (−∞,−9)
11) (6,∞)
- Answer
-
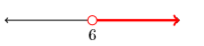
12) (5,∞)
13) {x|x>7}
- Answer
-

14) {x|x>−8}
15) [0,∞)
- Answer
-
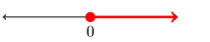
16) [7,∞)
17) {x|x≤−2}
- Answer
-

18) {x|x≤7}
19) (−∞,3]
- Answer
-
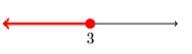
20) (−∞,−1]
In Exercises 21-28, use set-builder notation to describe the shaded region on the given number line.
21)
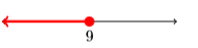
- Answer
-
{x|x≤9}
22)

23)
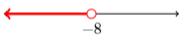
- Answer
-
{x|x<−8}
24)
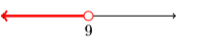
25)

- Answer
-
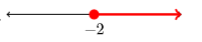
{x|x>−2}
26)
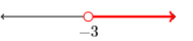
27)

- Answer
-
{x|x≥−3}
28)
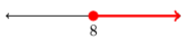
In Exercises 29-36, use interval notation to describe the shaded region on the given number line.
29)
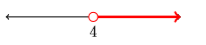
- Answer
-
(4,∞)
30)
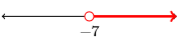
31)
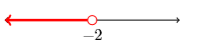
- Answer
-
(−∞,−2)
32)
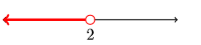
33)
- Answer
-
(−∞,5]
34)

35)

- Answer
-
[1,∞)
36)
In Exercises 37-44, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation to describe your solution.
37) x+10<19
- Answer
-
(−∞,9)
38) x+17≥7
39) 4x<8
- Answer
-
(−∞,2)
40) 16x≥−2
41) −2x≤−2
- Answer
-
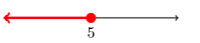
[1,∞)
42) −18x>−20
43) x−18>−10
- Answer
-
(8,∞)
44) x−8≤−18
In Exercises 45-62, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation to describe your solution.
45) −5x−6≥4−9x
- Answer
-
[5/2,∞)
46) 2x−7≥−3−4x
47) 16x−6≤18
- Answer
-
(−∞,3/2]
48) 8x−14≤−12
49) −14x−6≥−10−4x
- Answer
-
(−∞,2/5]
50) −13x−4≥−2−5x
51) 5x+18<38
- Answer
-
(−∞,4)
52) 9x+16<79
53) −16x−5≥−11−6x
- Answer
-
(−∞,3/5]
54) −11x−7≥−15−5x
55) 2x−9≥5−8x
- Answer
-
[7/5,∞)
56) −3x−6≥−2−9x
57) −10x−4≤18
- Answer
-
[−11/5,∞)
58) −6x−14≤1
59) −12x+4<−56
- Answer
-
(5,∞)
60) −18x+6<−12
61) 15x+5<6x+2
- Answer
-
(−∞,−1/3)
62) 12x+8<3x+5
In Exercises 63-76, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation describe your solution.
63) 32x>98
- Answer
-
(3/4,∞)
64) 67x>34
65) x+32<95
- Answer
-
(−∞,3/10)
66) x+14<−15
67) 47−16x≤43x−12
- Answer
-
[5/7,∞)
68) 53−34x≤74x−35
69) x−38≥−97
- Answer
-
[−51/56,∞)
70) x−72≥15
71) 65x≤−47
- Answer
-
[10/21,∞)
72) 43x≤29
73) −65x−73≤59−29x
- Answer
-
[−65/22,∞)
74) −37x−12≤32−27x
75) 97x+92>17x+72
- Answer
-
(−7/8,∞)
76) 57x+92>13x+52
In Exercises 77-84, solve each of the given inequalities. Sketch the solution on a number line, then use set-builder and interval notation containing fractions in reduced form to describe your solution.
77) −3.7x−1.98≤3.2
- Answer
-
[−7/5,∞)
78) −3.6x−3.32≤0.8
79) −3.4x+3.5≥0.9−2.2x
- Answer
-
(−∞,13/6]
80) −2.6x+3.1≥−2.9−1.7x
81) −1.3x+2.9>−2.6−3.3x
- Answer
-
(−11/4,∞)
82) 2.5x+2.1>1.4−3.8x
83) 2.2x+1.9<−2.3
- Answer
-
(−∞,−21/11)
84) 1.6x+1.2<1.6
Contributors and Attributions
David Arnold (Retired Professor (Mathematics) at College of the Redwoods)

