4.5E: Exercises

Last updated
Save as PDF

Page ID: 30512

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line

In the following exercises, use the graph to find the slope and $y$-intercept of each line. Compare the values to the equation $y=mx+b$.

Exercise $\PageIndex{1}$

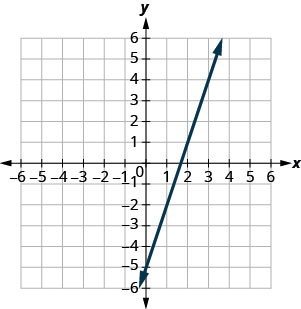
$The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, negative 5) and (1, negative 2).$

$y=3x−5$

Exercise $\PageIndex{2}$

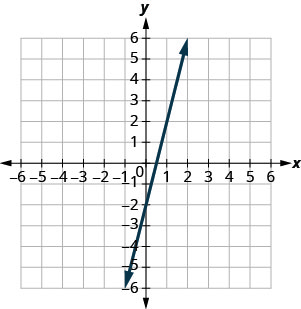
$y=4x−2$

Answer: slope $m=4$ and $y$-intercept $(0,−2)$

Exercise $\PageIndex{3}$

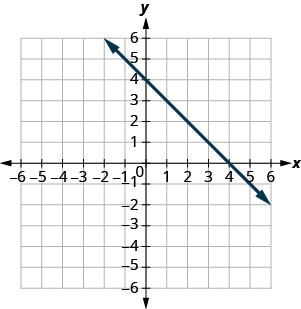
$y=−x+4$

Exercise $\PageIndex{4}$

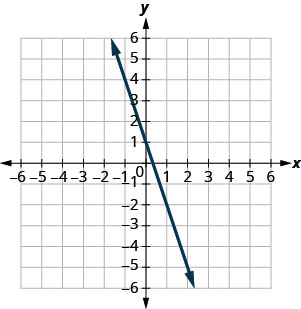
$y=−3x+1$

Answer: slope $m=−3$ and $y$-intercept $(0,1)$

Exercise $\PageIndex{5}$

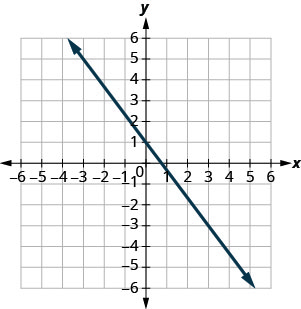
$y=-\frac{4}{3} x+1$

Exercise $\PageIndex{6}$

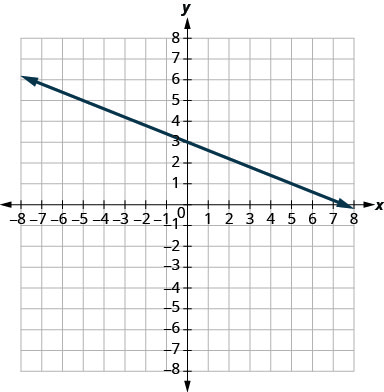
$y=-\frac{2}{5} x+3$

Answer: slope $m=-\frac{2}{5}$ and $y$ -intercept $(0,3)$

Identify the Slope and $y$-Intercept From an Equation of a Line

In the following exercises, identify the slope and $y$-intercept of each line.

Exercise $\PageIndex{7}$

$y=−7x+3$

Exercise $\PageIndex{8}$

$y=−9x+7$

Answer: $m = −9$; $y$-intercept: $(0,7)$

Exercise $\PageIndex{9}$

$y=6x−8$

Exercise $\PageIndex{10}$

$y=4x−10$

Answer: $m = 4$; $y$-intercept: $(0,−10)$

Exercise $\PageIndex{11}$

$3x+y=5$

Exercise $\PageIndex{12}$

$4x+y=8$

Answer: $m = −4\0; \(y$-intercept: $(0,8)$

Exercise $\PageIndex{13}$

$6x+4y=12$

Exercise $\PageIndex{14}$

$8x+3y=12$

Answer: $m = -\frac{8}{3}$; $y$-intercept: $(0,4)$

Exercise $\PageIndex{15}$

$5x−2y=6$

Exercise $\PageIndex{16}$

$7x−3y=9$

Answer: $m = \frac{7}{3}$; $y$-intercept: $(0,-3)$

Graph a Line Using Its Slope and Intercept

In the following exercises, graph the line of each equation using its slope and $y$-intercept.

Exercise $\PageIndex{17}$

$y=x+3$

Exercise $\PageIndex{18}$

$y=x+4$

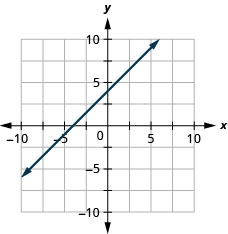
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, 4) and (1, 5).$

Exercise $\PageIndex{19}$

$y=3x−1$

Exercise $\PageIndex{20}$

$y=2x−3$

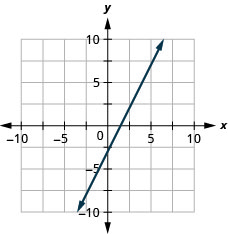
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, negative 3) and (1, negative 1).$

Exercise $\PageIndex{21}$

$y=−x+2$

Exercise $\PageIndex{22}$

$y=−x+3$

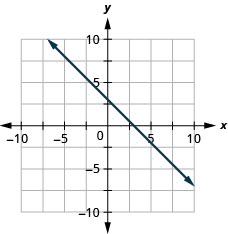
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, 3) and (1, 2).$

Exercise $\PageIndex{23}$

$y=−x−4$

Exercise $\PageIndex{24}$

$y=−x−2$

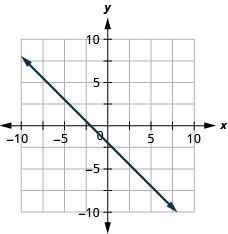
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, negative 2) and (1, negative 3).$

Exercise $\PageIndex{25}$

$y=-\frac{3}{4}x-1$

Exercise $\PageIndex{26}$

$y=-\frac{2}{5}x-3$

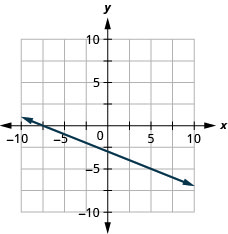
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, negative 3) and (5, negative 5).$

Exercise $\PageIndex{27}$

$y=-\frac{3}{5}x+2$

Exercise $\PageIndex{28}$

$y=-\frac{2}{3}x+1$

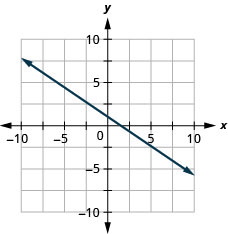
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0,1) and (3, negative 1).$

Exercise $\PageIndex{29}$

$3x−4y=8$

Exercise $\PageIndex{30}$

$4x−3y=6$

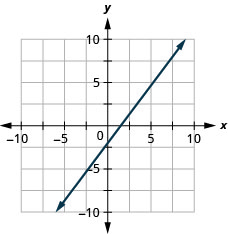
Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, negative 2) and (3,2).$

Exercise $\PageIndex{31}$

$y=0.1x+15$

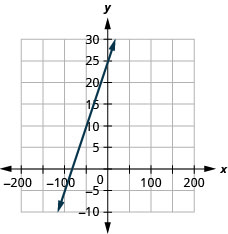
Exercise $\PageIndex{32}$

$y=0.3x+25$

Answer: $The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The line goes through the points (0, 25) and (negative 50, 10).$

Choose the Most Convenient Method to Graph a Line

In the following exercises, determine the most convenient method to graph each line.

Exercise $\PageIndex{33}$

$x=2$

Exercise $\PageIndex{34}$

$y=4$

Answer: horizontal line

Exercise $\PageIndex{35}$

$y=5$

Exercise $\PageIndex{36}$

$x=−3$

Answer: vertical line

Exercise $\PageIndex{37}$

$y=−3x+4$

Exercise $\PageIndex{38}$

$y=−5x+2$

Answer: slope–intercept

Exercise $\PageIndex{39}$

$x−y=5$

Exercise $\PageIndex{40}$

$x−y=1$

Answer: intercepts

Exercise $\PageIndex{41}$

$y=\frac{2}{3} x-1$

Exercise $\PageIndex{42}$

$y=\frac{4}{5} x-3$

Answer: slope–intercept

Exercise $\PageIndex{43}$

$y=−3$

Exercise $\PageIndex{44}$

$y=−1$

Answer: horizontal line

Exercise $\PageIndex{45}$

$3x−2y=−12$

Exercise $\PageIndex{46}$

$2x−5y=−10$

Answer: intercepts

Exercise $\PageIndex{47}$

$y=-\frac{1}{4}x+3$

Exercise $\PageIndex{48}$

$y=-\frac{1}{3} x+5$

Answer: slope–intercept

Graph and Interpret Applications of Slope–Intercept

Exercise $\PageIndex{49}$

The equation $P=31+1.75w$ models the relation between the amount of Tuyet’s monthly water bill payment, $P$, in dollars, and the number of units of water, $w$, used.

Find Tuyet’s payment for a month when $0$ units of water are used.
Find Tuyet’s payment for a month when $12$ units of water are used.
Interpret the slope and $P$-intercept of the equation.
Graph the equation.

Exercise $\PageIndex{50}$

The equation $P=28+2.54w$ models the relation between the amount of Randy’s monthly water bill payment, $P$, in dollars, and the number of units of water, $w$, used.

Find the payment for a month when Randy used $0$ units of water.
Find the payment for a month when Randy used $15$ units of water.
Interpret the slope and $P$-intercept of the equation.
Graph the equation.

Answer

$$28$
$$66.10$
The slope, $2.54$, means that Randy’s payment, $P$, increases by $$2.54$ when the number of units of water he used, $w$, ncreases by $1$. The $P$-intercept means that if the number units of water Randy used was $0$, the payment would be $$28$.

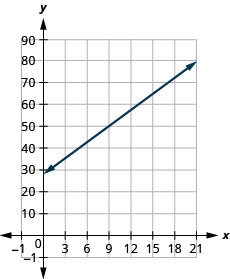
$The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable w and runs from negative 2 to 20. The y-axis of the plane represents the variable P and runs from negative 1 to 100. The line begins at the point (0, 28) and goes through the point (15, 66.1).$

Exercise $\PageIndex{51}$

Bruce drives his car for his job. The equation $R=0.575m+42$ models the relation between the amount in dollars, $R$, that he is reimbursed and the number of miles, $m$, he drives in one day.

Find the amount Bruce is reimbursed on a day when he drives $0$ miles.
Find the amount Bruce is reimbursed on a day when he drives $220$ miles.
Interpret the slope and $R$-intercept of the equation.
Graph the equation.

Exercise $\PageIndex{52}$

Janelle is planning to rent a car while on vacation. The equation $C=0.32m+15$ models the relation between the cost in dollars, $C$, per day and the number of miles, $m$, she drives in one day.

Find the cost if Janelle drives the car $0$ miles one day.
Find the cost on a day when Janelle drives the car $400$ miles.
Interpret the slope and $C$-intercept of the equation.
Graph the equation.

Answer

$$15$
$$143$
The slope, $0.32$, means that the cost, $C$, increases by $$0.32$ when the number of miles driven, $m$, increases by $1$. The $C$-intercept means that if Janelle drives $0$ miles one day, the cost would be $$15$.

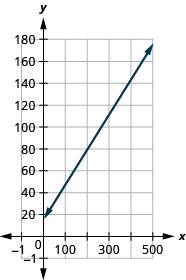
$The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable m and runs from negative 1 to 500. The y-axis of the plane represents the variable C and runs from negative 1 to 200. The line begins at the point (0,15) and goes through the point (400,143).$

Exercise $\PageIndex{53}$

Cherie works in retail and her weekly salary includes commission for the amount she sells. The equation $S=400+0.15c$ models the relation between her weekly salary, $S$, in dollars and the amount of her sales, $c$, in dollars.

Find Cherie’s salary for a week when her sales were $0$.
Find Cherie’s salary for a week when her sales were $3600$.
Interpret the slope and $S$-intercept of the equation.
Graph the equation.

Exercise $\PageIndex{54}$

Patel’s weekly salary includes a base pay plus commission on his sales. The equation $S=750+0.09c$ models the relation between his weekly salary, $S$, in dollars and the amount of his sales, $c$, in dollars.

Find Patel’s salary for a week when his sales were $0$.
Find Patel’s salary for a week when his sales were $18,540$.
Interpret the slope and $S$-intercept of the equation.
Graph the equation.

Answer

$$750$
$$2418.60$
The slope, $0.09$, means that Patel’s salary, $S$, increases by $$0.09$ for every $$1$ increase in his sales. The $S$-intercept means that when his sales are $$0$, his salary is $$750$.

$The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable w and runs from negative 1 to 20000. The y-axis of the plane represents the variable P and runs from negative 1 to 3000. The line begins at the point (0, 750) and goes through the point (18540, 2415).$

Exercise $\PageIndex{55}$

Costa is planning a lunch banquet. The equation $C=450+28g$ models the relation between the cost in dollars, $C$, of the banquet and the number of guests, $g$.

Find the cost if the number of guests is $40$.
Find the cost if the number of guests is $80$.
Interpret the slope and $C$-intercept of the equation.
Graph the equation.

Exercise $\PageIndex{56}$

Margie is planning a dinner banquet. The equation $C=750+42g$ models the relation between the cost in dollars, $C$, of the banquet and the number of guests, $g$.

Find the cost if the number of guests is $50$.
Find the cost if the number of guests is $100$.
Interpret the slope and $C$-intercept of the equation.
Graph the equation.

Answer

$$2850$
$$4950$
The slope, $42$, means that the cost, $C$, increases by $$42$ for when the number of guests increases by $1$. The $C$-intercept means that when the number of guests is $0$, the cost would be $$750$.

$The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable g and runs from negative 1 to 150. The y-axis of the plane represents the variable C and runs from negative 1 to 7000. The line begins at the point (0, 750) and goes through the point (100, 4950).$

Use Slopes to Identify Parallel Lines

In the following exercises, use slopes and $y$-intercepts to determine if the lines are parallel.

Exercise $\PageIndex{57}$

$y=\frac{3}{4} x-3 ; \quad 3x-4y=-2$

Exercise $\PageIndex{58}$

$y=\frac{2}{3} x-1 ; \quad 2x-3y=-2$

Answer: parallel

Exercise $\PageIndex{59}$

$2x-5y=-3; \quad y=\frac{2}{5} x+1$

Exercise $\PageIndex{60}$

$3x-4y=-2; \quad y=\frac{3}{4} x-3$

Answer: parallel

Exercise $\PageIndex{61}$

$2x-4y=6 ; \quad x-2y=3$

Exercise $\PageIndex{62}$

$6x−3y=9; \quad 2x−y=3$

Answer: not parallel

Exercise $\PageIndex{63}$

$4x+2y=6 ; \quad 6x+3y=3$

Exercise $\PageIndex{64}$

$8x+6y=6; \quad 12x+9y=12$

Answer: parallel

Exercise $\PageIndex{65}$

$x=5 ; \quad x=-6$

Exercise $\PageIndex{66}$

$x=7 ; \quad x=-8$

Answer: parallel

Exercise $\PageIndex{67}$

$x=-4 ; \quad x=-1$

Exercise $\PageIndex{68}$

$x=-3 ; \quad x=-2$

Answer: parallel

Exercise $\PageIndex{69}$

$y=2; \quad y=6$

Exercise $\PageIndex{70}$

$y=5; \quad y=1$

Answer: parallel

Exercise $\PageIndex{71}$

$y=−4; \quad y=3$

Exercise $\PageIndex{72}$

$y=−1; \quad y=2$

Answer: parallel

Exercise $\PageIndex{73}$

$x-y=2 ; \quad 2x-2y=4$

Exercise $\PageIndex{74}$

$4x+4y=8 ; \quad x+y=2$

Answer: not parallel

Exercise $\PageIndex{75}$

$x-3y=6 ; \quad 2x-6y=12$

Exercise $\PageIndex{76}$

$5x-2y=11 ; \quad 5x-y=7$

Answer: not parallel

Exercise $\PageIndex{77}$

$3x-6y=12; \quad 6x-3y=3$

Exercise $\PageIndex{78}$

$4x-8y=16; \quad x-2y=4$

Answer: not parallel

Exercise $\PageIndex{79}$

$9x-3y=6; \quad 3x-y=2$

Exercise $\PageIndex{80}$

$x-5y=10; \quad 5x-y=-10$

Answer: not parallel

Exercise $\PageIndex{81}$

$7x-4y=8; \quad 4x+7y=14$

Exercise $\PageIndex{82}$

$9x-5y=4; \quad 5x+9y=-1$

Answer: not parallel

Use Slopes to Identify Perpendicular Lines

In the following exercises, use slopes and $y$-intercepts to determine if the lines are perpendicular.

Exercise $\PageIndex{83}$

$3x-2y=8; \quad 2x+3y=6$

Exercise $\PageIndex{84}$

$x-4y=8; \quad 4x+y=2$

Answer: perpendicular

Exercise $\PageIndex{85}$

$2x+5y=3; \quad 5x-2y=6$

Exercise $\PageIndex{86}$

$2x+3y=5; \quad 3x-2y=7$

Answer: perpendicular

Exercise $\PageIndex{87}$

$3x-2y=1; \quad 2x-3y=2$

Exercise $\PageIndex{88}$

$3x-4y=8; \quad 4x-3y=6$

Answer: not perpendicular

Exercise $\PageIndex{89}$

$5x+2y=6; \quad 2x+5y=8$

Exercise $\PageIndex{90}$

$2x+4y=3; \quad 6x+3y=2$

Answer: not perpendicular

Exercise $\PageIndex{91}$

$4x-2y=5; \quad 3x+6y=8$

Exercise $\PageIndex{92}$

$2x-6y=4; \quad 12x+4y=9$

Answer: perpendicular

Exercise $\PageIndex{93}$

$6x-4y=5; \quad 8x+12y=3$

Exercise $\PageIndex{94}$

$8x-2y=7; \quad 3x+12y=9$

Answer: perpendicular

Everyday Math

Exercise $\PageIndex{95}$

The equation $C=\frac{5}{9} F-17.8$ can be used to convert temperatures, $F$, on the Fahrenheit scale to temperatures, $C$, on the Celsius scale.

Explain what the slope of the equation means.
Explain what the $C$-intercept of the equation means.

Exercise $\PageIndex{96}$

The equation $n=4T−160$ is used to estimate the number of cricket chirps, $n$, in one minute based on the temperature in degrees Fahrenheit, $T$.

Explain what the slope of the equation means.
Explain what the $n$-intercept of the equation means. Is this a realistic situation?

Answer

For every increase of one degree Fahrenheit, the number of chirps increases by four.
There would be $−160$ chirps when the Fahrenheit temperature is $0°$. (Notice that this does not make sense; this model cannot be used for all possible temperatures.)

Writing Exercises

Exercise $\PageIndex{97}$

Explain in your own words how to decide which method to use to graph a line.

Exercise $\PageIndex{98}$

Why are all horizontal lines parallel?

Answer: Answers will vary.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This table has eight rows and four columns. The first row is a header row and it labels each column. The first column is labeled "I can …", the second "Confidently", the third “With some help” and the last "No–I don’t get it". In the “I can…” column the next row reads “recognize the relation between the graph and the slope-intercept form of an equation of a line.” The third row reads “identify the Slope and y-intercept from an equation of a line”. The fourth row reads “graph a line using its slope and intercept”. The fifth row reads “choose the most convenient method to graph a line.” The sixth row reads “graph and interpret applications of slope-intercept”. The seventh row reads “use slopes to identify parallel lines” and the last row reads “use slopes to identify perpendicular lines.” The remaining columns are blank.$

b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

Practice Makes Perfect

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)

Exercise \(\PageIndex{61}\)

Exercise \(\PageIndex{62}\)

Exercise \(\PageIndex{63}\)

Exercise \(\PageIndex{64}\)

Exercise \(\PageIndex{65}\)

Exercise \(\PageIndex{66}\)

Exercise \(\PageIndex{67}\)

Exercise \(\PageIndex{68}\)

Exercise \(\PageIndex{69}\)

Exercise \(\PageIndex{70}\)

Exercise \(\PageIndex{71}\)

Exercise \(\PageIndex{72}\)

Exercise \(\PageIndex{73}\)

Exercise \(\PageIndex{74}\)

Exercise \(\PageIndex{75}\)

Exercise \(\PageIndex{76}\)

Exercise \(\PageIndex{77}\)

Exercise \(\PageIndex{78}\)

Exercise \(\PageIndex{79}\)