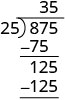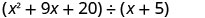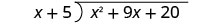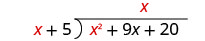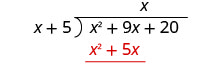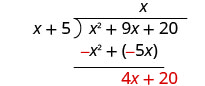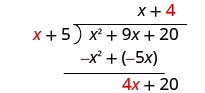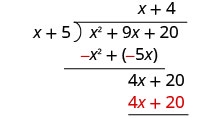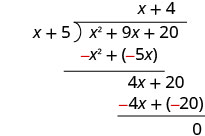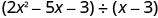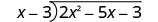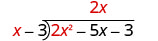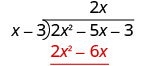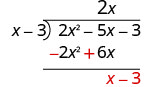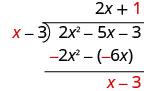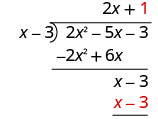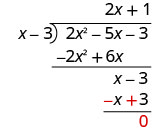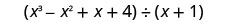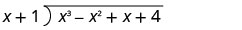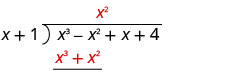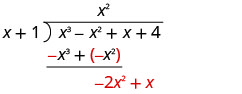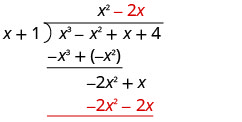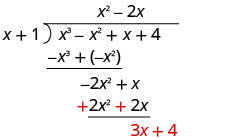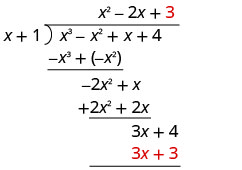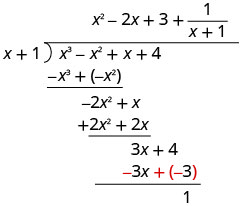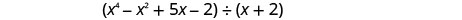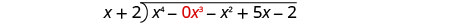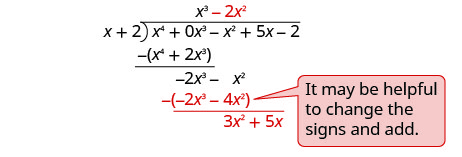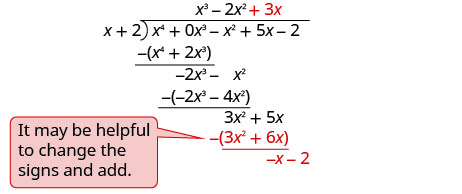Divide a Polynomial by a Monomial
In the last section, you learned how to divide a monomial by a monomial. As you continue to build up your knowledge of polynomials the next procedure is to divide a polynomial of two or more terms by a monomial.
The method we’ll use to divide a polynomial by a monomial is based on the properties of fraction addition. So we’ll start with an example to review fraction addition.
\(\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}\)
Now we will do this in reverse to split a single fraction into separate fractions.
We’ll state the fraction addition property here just as you learned it and in reverse.
FRACTION ADDITION
If a,b, and c are numbers where \(c\neq 0\), then
\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]
We use the form on the left to add fractions and we use the form on the right to divide a polynomial by a monomial.
We use this form of fraction addition to divide polynomials by monomials.
DIVISION OF A POLYNOMIAL BY A MONOMIAL
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Example \(\PageIndex{1}\)
Find the quotient:\(\dfrac{7 y^{2}+21}{7}\)
Solution
\(\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}\)
Try It \(\PageIndex{2}\)
Find the quotient: \(\dfrac{8 z^{2}+24}{4}\)
- Answer
-
\(2 z^{2}+6\)
Try It \(\PageIndex{3}\)
Find the quotient:\(\dfrac{18 z^{2}-27}{9}\)
- Answer
-
\(2 z^{2}-3\)
Remember that division can be represented as a fraction. When you are asked to divide a polynomial by a monomial and it is not already in fraction form, write a fraction with the polynomial in the numerator and the monomial in the denominator.
Example \(\PageIndex{4}\)
Find the quotient: \(\left(18 x^{3}-36 x^{2}\right) \div 6 x\)
Solution
\(\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}\)
Try It \(\PageIndex{5}\)
Find the quotient: \(\left(27 b^{3}-33 b^{2}\right) \div 3 b\)
- Answer
-
\(9 b^{2}-11 b\)
Try It \(\PageIndex{6}\)
Find the quotient: \(\left(25 y^{3}-55 y^{2}\right) \div 5 y\)
- Answer
-
\(5 y^{2}-11 y\)
When we divide by a negative, we must be extra careful with the signs.
Example \(\PageIndex{7}\)
Find the quotient: \(\dfrac{12 d^{2}-16 d}{-4}\)
Solution
\(\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}\)
Try It \(\PageIndex{8}\)
Find the quotient: \(\dfrac{25 y^{2}-15 y}{-5}\)
- Answer
-
\(-5 y^{2}+3 y\)
Try It \(\PageIndex{9}\)
Find the quotient: \(\dfrac{42 b^{2}-18 b}{-6}\)
- Answer
-
\(-7 b^{2}+3 b\)
Example \(\PageIndex{10}\)
Find the quotient: \(\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\)
Solution
\(\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}\)
Try It \(\PageIndex{11}\)
Find the quotient: \(\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}\)
- Answer
-
\(15 d^{4}+6 d^{2}\)
Try It \(\PageIndex{12}\)
Find the quotient: \(\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}\)
- Answer
-
\(36 p^{4}-8 p^{2}\)
Example \(\PageIndex{13}\)
Find the quotient: \(\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\)
Solution
\(\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}\)
Try It \(\PageIndex{14}\)
Find the quotient: \(\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)\)
- Answer
-
\(-4 a+2 b\)
Try It \(\PageIndex{15}\)
Find the quotient: \(\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)\)
- Answer
-
\(8 a^{5} b+6 a^{3} b^{2}\)
Example \(\PageIndex{16}\)
Find the quotient: \(\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\)
Solution
\(\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}\)
Try It \(\PageIndex{17}\)
Find the quotient: \(\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}\)
- Answer
-
\(5 x y+3 y-2 y^{2}\)
Try It \(\PageIndex{18}\)
Find the quotient: \(\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}\)
- Answer
-
\(5 a^{2}+2 a^{2} b-6 b^{2}\)
Example \(\PageIndex{19}\)
Find the quotient: \(\dfrac{10 x^{2}+5 x-20}{5 x}\)
Solution
\(\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}\)
Try It \(\PageIndex{20}\)
Find the quotient: \(\dfrac{18 c^{2}+6 c-9}{6 c}\)
- Answer
-
\(3 c+1-\dfrac{3}{2 c}\)
Try It \(\PageIndex{21}\)
Find the quotient: \(\dfrac{10 d^{2}-5 d-2}{5 d}\)
Solution
\(2 d-1-\dfrac{2}{5 d}\)
Divide a Polynomial by a Binomial
To divide a polynomial by a binomial, we follow a procedure very similar to long division of numbers. So let’s look carefully the steps we take when we divide a 3-digit number, 875, by a 2-digit number, 25.
| We write the long division |
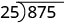 |
| We divide the first two digits, 87, by 25. |
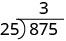 |
| We multiply 3 times 25 and write the product under the 87. |
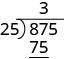 |
| Now we subtract 75 from 87. |
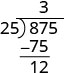 \[\begin{array}{c} \[\begin{array}{c}
3 \\
2 5 \longdiv { 8 7 5 } \\
-75 \\
\hline 125
\end{array}\] |
| Then we bring down the third digit of the dividend, 5. |
 |
| Repeat the process, dividing 25 into 125. |
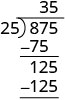 |
We check division by multiplying the quotient by the divisor.
If we did the division correctly, the product should equal the dividend.
\[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]
Now we will divide a trinomial by a binomial. As you read through the example, notice how similar the steps are to the numerical example above.
Try It \(\PageIndex{23}\)
Find the quotient: \(\left(y^{2}+10 y+21\right) \div(y+3)\)
- Answer
-
y+7
Try It \(\PageIndex{24}\)
Find the quotient: \(\left(m^{2}+9 m+20\right) \div(m+4)\)
- Answer
-
m+5
When the divisor has subtraction sign, we must be extra careful when we multiply the partial quotient and then subtract. It may be safer to show that we change the signs and then add.
Try It \(\PageIndex{26}\)
Find the quotient: \(\left(2 x^{2}-3 x-20\right) \div(x-4)\)
- Answer
-
2x+5
Try It \(\PageIndex{27}\)
Find the quotient: \(\left(3 x^{2}-16 x-12\right) \div(x-6)\)
- Answer
-
3x+2
When we divided 875 by 25, we had no remainder. But sometimes division of numbers does leave a remainder. The same is true when we divide polynomials. In Example \(\PageIndex{25}\), we’ll have a division that leaves a remainder. We write the remainder as a fraction with the divisor as the denominator.
Try It \(\PageIndex{29}\)
Find the quotient: \(\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)\)
- Answer
-
\(x^{2}+3 x+2+\dfrac{2}{x+2}\)
Try It \(\PageIndex{30}\)
Find the quotient: \(\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)\)
- Answer
-
\(2 x^{2}+6 x-5-\dfrac{3}{x+1}\)
Look back at the dividends in Example, Example, and Example. The terms were written in descending order of degrees, and there were no missing degrees. The dividend in Example will be \(x^{4}-x^{2}+5 x-2\). It is missing an \(x^{3}\) term. We will add in \(0x^{3}\) as a placeholder.
Example \(\PageIndex{31}\)
Find the quotient: \(\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)\)
Solution
Notice that there is no \(x^{3}\) term in the dividend. We will add \(0x^{3}\) as a placeholder.
| |
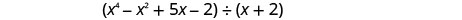 |
| Write it as a long division problem. Be sure the dividend is in standard form with placeholders for missing terms. |
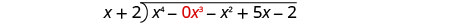 |
Divide x4 by x.
Put the answer, x3, in the quotient over the x3 term.
Multiply x3 times x + 2. Line up the like terms.
Subtract and then bring down the next term. |
 |
Divide −2x3 by x.
Put the answer, −2x2, in the quotient over the x2 term.
Multiply −2x2 times x + 1. Line up the like terms.
Subtract and bring down the next term. |
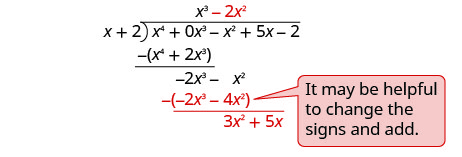 |
Divide 3x2 by x.
Put the answer, 3x, in the quotient over the x term.
Multiply 3x times x + 1. Line up the like terms.
Subtract and bring down the next term. |
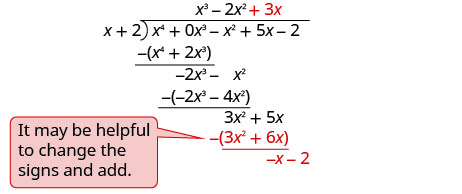 |
Divide −x by x.
Put the answer, −1, in the quotient over the constant term.
Multiply −1 times x + 1. Line up the like terms.
Change the signs, add. |
 |
| To check, multiply \((x+2)\left(x^{3}-2 x^{2}+3 x-1\right)\) |
|
| The result should be \(x^{4}-x^{2}+5 x-2\) |
Try It \(\PageIndex{32}\)
Find the quotient: \(\left(x^{3}+3 x+14\right) \div(x+2)\)
- Answer
-
\(x^{2}-2 x+7\)
Try It \(\PageIndex{33}\)
Find the quotient: \(\left(x^{4}-3 x^{3}-1000\right) \div(x+5)\)
- Answer
-
\(x^{3}-8 x^{2}+40 x-200\)
In Example \(\PageIndex{31}\), we will divide by \(2a−3\). As we divide we will have to consider the constants as well as the variables.
Example \(\PageIndex{34}\)
Find the quotient: \(\left(8 a^{3}+27\right) \div(2 a+3)\)
Solution
This time we will show the division all in one step. We need to add two placeholders in order to divide.
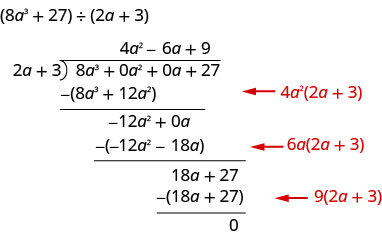
To check, multiply \((2 a+3)\left(4 a^{2}-6 a+9\right)\)
The result should be \(8 a^{3}+27\)
Try It \(\PageIndex{35}\)
Find the quotient: \(\left(x^{3}-64\right) \div(x-4)\)
- Answer
-
\(x^{2}+4 x+16\)
Try It \(\PageIndex{36}\)
Find the quotient: \(\left(125 x^{3}-8\right) \div(5 x-2)\)
- Answer
-
\(25 x^{2}+10 x+4\)
Note
Access these online resources for additional instruction and practice with dividing polynomials:
- Divide a Polynomial by a Monomial
- Divide a Polynomial by a Monomial 2
- Divide Polynomial by Binomial



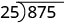
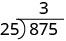
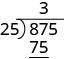
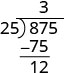 \[\begin{array}{c}
\[\begin{array}{c}