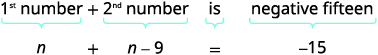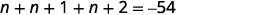2.2: Use a Problem Solving Strategy
- Last updated
- Jan 7, 2020
- Save as PDF
- Page ID
- 30817
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Use a problem solving strategy for word problems
- Solve number word problems
- Solve percent applications
- Solve simple interest applications
Before you get started, take this readiness quiz.
Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.
Start with a fresh slate and begin to think positive thoughts. Repeating some of the following statements may be helpful to turn your thoughts positive. Thinking positive thoughts is a first step towards success.
- I think I can! I think I can!
- While word problems were hard in the past, I think I can try them now.
- I am better prepared now—I think I will begin to understand word problems.
- I am able to solve equations because I practiced many problems and I got help when I needed it—I can try that with word problems.
- It may take time, but I can begin to solve word problems.
- You are now well prepared and you are ready to succeed. If you take control and believe you can be successful, you will be able to master word problems.
Use a Problem Solving Strategy for Word Problems
Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.
EXAMPLE 2.2.1
Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?
Solution:
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | What was the snowfall last season? |
| Step 3. Name what we are looking for and choose a variable to represent it. | Let s= the snowfall last season. |
| Step 4. Translate. Restate the problem in one sentence with all the important information. |  |
| Translate into an equation. |  |
| Step 5. Solve the equation. | 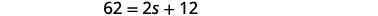 |
| Subtract 12 from each side. | 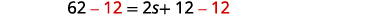 |
| Simplify. |  |
| Divide each side by two. |  |
| Simplify. |  |
| Step 6. Check: First, is our answer reasonable? Yes, having 25 inches of snow seems OK. The problem says the normal snowfall is twelve inches more than twice the number of last season. Twice 25 is 50 and 12 more than that is 62. | |
| Step 7. Answer the question. | The snowfall last season was 25 inches. |
Try It! 2.2.1
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was three more than twice the number of notebooks. He bought seven textbooks. How many notebooks did he buy?
- Answer
-
He bought two notebooks
Try It! 2.2.2
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
- Answer
-
He did seven crossword puzzles
We summarize an effective strategy for problem solving.
PROBLEM SOLVING STRATEGY FOR WORD PROBLEMS
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using proper algebra techniques.
- Check the answer in the problem to make sure it makes sense.
- Answer the question with a complete sentence.
Solve Number Word Problems
We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.
EXAMPLE 2.2.2
The sum of seven times a number and eight is thirty-six. Find the number.
Solution:
| Step 1. Read the problem. | |
|---|---|
| Step 2. Identify what you are looking for. | the number |
|
Step 3. Name what you are looking for and choose a variable to represent it. |
Let n= the number. |
|
Step 4. Translate: Restate the problem as one sentence. Translate into an equation. |
|
|
Step 5. Solve the equation. Subtract eight from each side and simplify. Divide each side by seven and simplify. |
|
|
Step 6. Check. Is the sum of seven times four plus eight equal to 36? 7·4+8?=3628+8?=3636=36✓ |
|
| Step 7. Answer the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
Try It! 2.2.3
The sum of four times a number and two is fourteen. Find the number.
- Answer
-
3
Try It! 2.2.4
The sum of three times a number and seven is twenty-five. Find the number.
- Answer
-
6
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
EXAMPLE 2.2.3
The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.
Solution:
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | two numbers |
| Step 3. Name what you are looking for by choosing a variable to represent the first number. “One number is nine less than the other.” | Let n=1st number. n−9=2nd number |
| Step 4. Translate. Write as one sentence. Translate into an equation. | The sum of two numbers is negative fifteen.
|
|
Step 5. Solve the equation. Combine like terms. Add nine to each side and simplify. Simplify. |
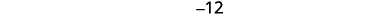 |
| Step 6. Check. Is −12 nine less than −3? −3−9?=−12−12=−12✓ Is their sum −15? −3+(−12)?=−15−15=−15✓ | |
| Step 7. Answer the question. | The numbers are −3 and −12. |
Try It! 2.2.5
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
- Answer
-
−15,−8
Try It! 2.2.6
The sum of two numbers is negative eighteen. One number is forty more than the other. Find the numbers.
- Answer
-
−29,11
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:
1,2,3,4−10,−9,−8,−7150,151,152,153
Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as n, the next consecutive integer is n+1. The one after that is one more than n+1, so it is n+1+1, which is n+2.
n1stintegern+12ndconsecutive integern+23rdconsecutive integeretc.
We will use this notation to represent consecutive integers in the next example.
EXAMPLE 2.2.4
Find three consecutive integers whose sum is −54.
Solution:
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | three consecutive integers |
| Step 3. Name each of the three numbers | Let n=1stinteger. n+1=2ndconsecutive integer n+2=3rdconsecutive integer |
| Step 4. Translate. Restate as one sentence. Translate into an equation. | The sum of the three integers is −54.
|
| Step 5. Solve the equation. Combine like terms. Subtract three from each side. Divide each side by three. | 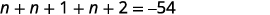 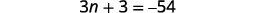 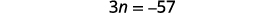 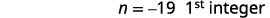
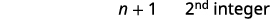 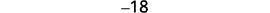 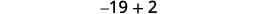 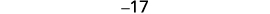 |
| Step 6. Check. −19+(−18)+(−17)=−54−54=−54✓ | |
| Step 7. Answer the question. | The three consecutive integers are −17,−18, and −19. |
Try It! 2.2.7
Find three consecutive integers whose sum is −96.
- Answer
-
−33,−32,−31
Try It! 2.2.8
Find three consecutive integers whose sum is −36.
- Answer
-
−13,−12,−11
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
24,26,28
−12,−10,−8
Notice each integer is two more than the number preceding it. If we call the first one n, then the next one is n+2. The one after that would be n+2+2 or n+4.
n1stintegern+12ndconsecutive integern+23rdconsecutive integeretc.
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 63, 65, and 67.
63,65,67
n,n+2,n+4
n1stintegern+12ndconsecutive integern+23rdconsecutive integeretc.
Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.
EXAMPLE 2.2.5
Find three consecutive even integers whose sum is 120.
Solution:
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | three consecutive even integers |
| Step 3. Name each of the three numbers |
Let n=1stconsecutive even integer. n+2=2ndconsecutive even integer. n+4=3rdconsecutive even integer. |
| Step 4. Translate.
Restate as one sentence. Translate into an equation. |
The sum of the three even integers is 120 n+n+2+n+4=120 |
| Step 5. Solve the equation.
Combine like terms. Subtract three from each side. Divide each side by three. |
n+n+2+n+4=120 3n+6=1203n=114n=381stinteger n+22ndinteger38+240 n+23rdinteger38+442 |
| Step 6. Check. 38+40+42?=120120=120✓ | |
| Step 7. Answer the question. | The three consecutive integers are 38, 40, and 42. |
Try It! 2.2.9
Find three consecutive even integers whose sum is 102.
- Answer
-
32,34,36
Try It! 2.2.10
Find three consecutive even integers whose sum is −24.
- Answer
-
−10,−8,−6
When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.
EXAMPLE 2.2.6
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
Solution:
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | How much does the husband earn? |
| Step 3. Name each of the three numbers |
Let h=the amount the husband earns. |
| Step 4. Translate.
Restate the problem in one sentence with all the important information. Translate into an equation. |
2h−16,000=the amount the wife earns. Together the husband and wife earn $110,000. h+2h−16,000=110,000 |
| Step 5. Solve the equation.
Combine like terms. Add 16,000 to both sides and simplify. Divide each side by three. |
h+2h−16,000=110,000 3h−16,000=110,0003h=126,000h=42,000amount husband earns 2h−16,000 amount wife earns2(42,000)−16,00084,000−16,00068,000 |
| Step 6. Check. If the wife earns $68,000 and the husband earns $42,000, is that $110,000? Yes! | |
| Step 7. Answer the question. | The husband earns $42,000 a year. |
According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,400. This was $1,600 less than six times the cost in 1975. What was the average cost of a car in 1975?
- Answer
-
The average cost was $5,000.
Try It! 2.2.11
US Census data shows that the median price of new home in the U.S. in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?
- Answer
-
The median price was $19,300.
Solve Percent Applications
There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.
EXAMPLE 2.2.7
Translate and solve:
- What number is 45% of 84?
- 8.5% of what amount is $4.76?
- 168 is what percent of 112?
Solution:
a.
 |
|
| Translate into algebra. Let n = the number. | 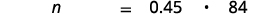 |
| Multiply. | 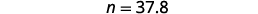 |
| 37.8 is 45% of 84. |
b.
 |
|
| Translate. Let n= the amount. | 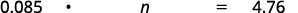 |
| Multiply. | 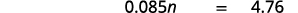 |
| Divide both sides by 0.085 and simplify. |  |
| 8.5% of $56 is $4.76 |
c.
| We are asked to find percent, so we must have our result in percent form. |  |
| Translate into algebra. Let p= the percent. | 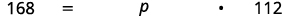 |
| Multiply. |  |
| Divide both sides by 112 and simplify. | .jpg?revision=1&size=bestfit&width=285&height=17) |
| Convert to percent. |  |
| 168 is 150% of 112. |
Try It! 2.2.12
Translate and solve:
- What number is 45% of 80?
- 7.5% of what amount is $1.95?
- 110 is what percent of 88?
- Answer
-
a. 36 b. $26 c. 125%
Try It! 2.2.13
Translate and solve:
- What number is 55% of 60?
- 8.5% of what amount is $3.06?
- 126 is what percent of 72?
- Answer
-
a. 33 b. $36 c. 175%
Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.
EXAMPLE 2.2.8
The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?
Solution:
| What are you asked to find? | What total amount of protein is recommended? |
| Choose a variable to represent it. | Let a= total amount of protein. |
| Write a sentence that gives the information to find it. | 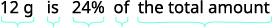 |
| Translate into an equation. |  |
| Solve. |  |
| Check: Does this make sense? Yes, 24% is about 14 of the total and 12 is about 14 of 50. | |
| Write a complete sentence to answer the question. | The amount of protein that is recommended is 50 g. |
Try It! 2.2.14
One serving of wheat square cereal has 7 grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?
- Answer
-
25 grams
Try It! 2.2.15
One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?
- Answer
-
2,375 mg
Remember to put the answer in the form requested. In the next example we are looking for the percent.
EXAMPLE 2.2.9
Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?
Solution:
| What are you asked to find? | What percent of the total calories is fat? |
| Choose a variable to represent it. | Let p= percent of fat. |
| Write a sentence that gives the information to find it. |  |
| Translate the sentence into an equation. |  |
| Multiply. |  |
| Divide both sides by 240. |  |
| Put in percent form. |  |
| Check: does this make sense? Yes, 25% is one-fourth; 60 is one-fourth of 240. So, 25% makes sense. | |
| Write a complete sentence to answer the question. | Of the total calories in each muffin, 25% is fat. |
Try It! 2.2.16
Mitzi received some gourmet brownies as a gift. The wrapper said each 28% brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat? Round the answer to the nearest whole percent.
- Answer
-
50%
Try It! 2.2.17
The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat? Round the answer to the nearest whole percent.
- Answer
-
40%
It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change.
To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.
FIND PERCENT CHANGE
- Find the amount of change.
change=new amount−original amount
- Find what percent the amount of change is of the original amount.
change is what percent of the original amount?
EXAMPLE 2.2.10
Recently, the California governor proposed raising community college fees from $36 a unit to $46 a unit. Find the percent change. (Round to the nearest tenth of a percent.)
Solution:
| Find the amount of change. | 46−36=10 |
| Find the percent. | Change is what percent of the original amount? |
| Let p= the percent. |  |
| Translate to an equation. | 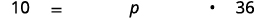 |
| Simplify. | 10=36p |
| Divide both sides by 36. | 0.278≈p |
| Change to percent form; round to the nearest tenth | 27.8%≈p |
| Write a complete sentence to answer the question. | The new fees are approximately a 27.8% increase over the old fees. |
| Remember to round the division to the nearest thousandth in order to round the percent to the nearest tenth. | |
Try It! 2.2.18
Find the percent change. (Round to the nearest tenth of a percent.) In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.
- Answer
-
8.8%
Try It! 2.2.19
Find the percent change. (Round to the nearest tenth of a percent.) In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was 2.25.
- Answer
-
50
Applications of discount and mark-up are very common in retail settings.
When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price.
The price a retailer pays for an item is called the original cost. The retailer then adds a mark-up to the original cost to get the list price, the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.
DISCOUNT
\begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}
The sale price should always be less than the original price.
MARK-UP
\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}
The list price should always be more than the original cost.
EXAMPLE \PageIndex{11}
Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find
- the amount of mark-up and
- the list price of the painting.
Solution:
a.
| Identify what you are asked to find, and choose a variable to represent it. | What is the amount of mark-up? Let m= the amount of mark-up. |
| Write a sentence that gives the information to find it. | 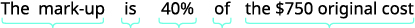 |
| Translate into an equation. |  |
| Solve the equation. |  |
| Write a complete sentence. | The mark-up on the painting was $300. |
| Identify what you are asked to find, and choose a variable to represent it. | What is the list price? Let p= the list price. |
| Write a sentence that gives the information to find it. |  |
| Translate into an equation. | 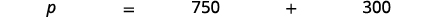 |
| Solve the equation. |  |
| Check. | Is the list price more than the original cost? Is $1,050 more than $750? Yes. |
| Write a complete sentence. | The list price of the painting was $1,050. |
Try It! \PageIndex{20}
Find a. the amount of mark-up and b. the list price: Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.
- Answer
-
a. $600 b. $1,800
Try It! \PageIndex{21}
Find a. the amount of mark-up and b. the list price: The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.
- Answer
-
a. $2,975 b. $11,475
Solve Simple Interest Applications
Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.
The amount of money you initially deposit into a bank is called the principal, P, and the bank pays you interest, I. When you take out a loan, you pay interest on the amount you borrow, also called the principal.
In either case, the interest is computed as a certain percent of the principal, called the rate of interest, r. The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable t, (for time) represents the number of years the money is saved or borrowed.
Interest is calculated as simple interest or compound interest. Here we will use simple interest.
SIMPLE INTEREST
If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is
\begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}
Interest earned or paid according to this formula is called simple interest.
The formula we use to calculate interest is I=Prt. To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
EXAMPLE \PageIndex{12}
Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?
Solution:
\begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}
\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}
Try It! \PageIndex{22}
Nathaly deposited $12,500 in her bank account where it will earn 4% simple interest. How much interest will Nathaly earn in five years?
- Answer
-
He will earn $2,500.
Try It! \PageIndex{23}
Susana invested a principal of $36,000 in her bank account that earned simple interest at an interest rate of 6.5%. How much interest did she earn in three years?
- Answer
-
She earned $7,020.
There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.
EXAMPLE \PageIndex{13}
Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?
Solution:
\begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}
\text{Identify what you are asked to find,} \qquad \quad \text{What is rate of simple interest?} \\ \begin{align*} &\text{and choose a variable to represent it.} & \text{Let }r \;&= \;\text{ rate of interest} \\ &\text{Write the formula.} & I \;&= \;Prt \\ &\text{Substitute in the given information.} & 1,500\; &= \;(7,500)r(5) \\ &\text{Multiply.} & 1,500 \; &= \; 37,500r \\ &\text{Divide.} & 0.04 \; &=\; r \\ &\text{Change to percent form} & r\; &= \; 4\% \end{align*}
Check.
\begin{align*} I \; &= \; Prt \\ 1,500 \; &\stackrel{?}{=}\; (7,500)(0.04)(5)\\ 1,500 \; &= \;1,500✓ \end{align*}
Write a complete sentence. The rate of interest was 4\%.
Try It! \PageIndex{24}
Jim lent his sister $5,000 to help her buy a house. In three years, she paid him the $5,000, plus $900 interest. What was the rate of simple interest?
- Answer
-
The rate of simple interest was 6%.
Try It! \PageIndex{25}
Loren lent his brother $3,000 to help him buy a car. In four years, his brother paid him back the $3,000 plus $660 in interest. What was the rate of simple interest?
- Answer
-
The rate of simple interest was 5.5%.
In the next example, we are asked to find the principal—the amount borrowed.
EXAMPLE \PageIndex{14}
Sean’s new car loan statement said he would pay $4,866,25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?
Solution:
\begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}
\text{Identify what you are asked to find,} \qquad \quad \text{What is the amount borrowed (the principal)?} \\ \begin{align*} &\text{and choose a variable to represent it.} & \text{Let }P \;&= \;\text{ principal borrowed} \\ &\text{Write the formula.} & I \;&= \;Prt \\ &\text{Substitute in the given information.} & 4,866.25\; &= \;P(0.085)(5) \\ &\text{Multiply.} & 4,866.25 \; &= \; 0.425P \\ &\text{Divide.} & 11,450 \; &=\; P \end{align*}
Check.
\begin{align*} I \; &= \; Prt \\ 4,866.25 \; &\stackrel{?}{=}\; (11,450)(0.085)(5)\\ 4,866.25 \; &= \;4,866.25✓ \end{align*}
Write a complete sentence. The principal was $11,450.
Try It! \PageIndex{26}
Eduardo noticed that his new car loan papers stated that with a 7.5% simple interest rate, he would pay $6,596.25 in interest over five years. How much did he borrow to pay for his car?
- Answer
-
He paid $17,590.
Try It! \PageIndex{27}
In five years, Gloria’s bank account earned $2,400 interest at 5% simple interest. How much had she deposited in the account?
- Answer
-
She deposited $9,600.
Access this online resource for additional instruction and practice with using a problem solving strategy.
- Begining Arithmetic Problems
Key Concepts
- How To Use a Problem Solving Strategy for Word Problems
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using proper algebra techniques.
- Check the answer in the problem to make sure it makes sense.
- Answer the question with a complete sentence.
- How To Find Percent Change
- Find the amount of change
\text{change}=\text{new amount}−\text{original amount}
- Find what percent the amount of change is of the original amount.
\text{change is what percent of the original amount?}
- Find the amount of change
- \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}
- \begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}
- If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is: \begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}