3.3E: Exercises

Last updated
Save as PDF

Page ID: 30828

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Practice Makes Perfect

Find an Equation of the Line Given the Slope and y-Intercept

In the following exercises, find the equation of a line with given slope and y-intercept. Write the equation in slope-intercept form.

1. slope $3$ and $y$-intercept $(0,5)$

Answer: $y=3x+5$

2. slope $8$ and $y$-intercept $(0,−6)$

3. slope $−3$ and $y$-intercept $(0,−1)$

Answer: $y=−3x−1$

4. slope $−1$ and $y$-intercept $(0,3)$

5. slope $\frac{1}{5}$ and $y$-intercept $(0,−5)$

Answer: $y=\frac{1}{5}x−5$

6. slope $−\frac{3}{4}$ and $y$-intercept $(0,−2)$

7. slope $0$ and $y$-intercept $(0,−1)$

Answer: $y=−1$

8. slope $−4$ and $y$-intercept $(0,0)$

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope-intercept form.

9.
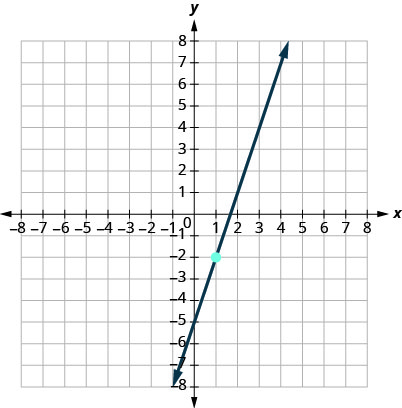
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 5), (1, negative 2), and (2, 1).$

Answer: $y=3x−5$

10.
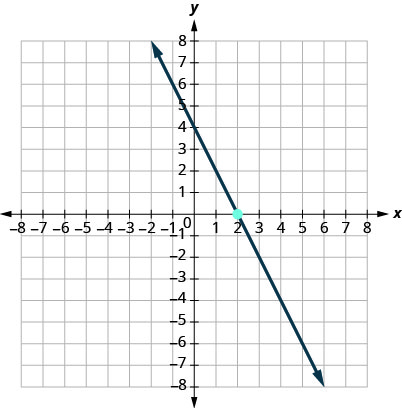
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 4), (1, 2), and (2, 0).$

11.
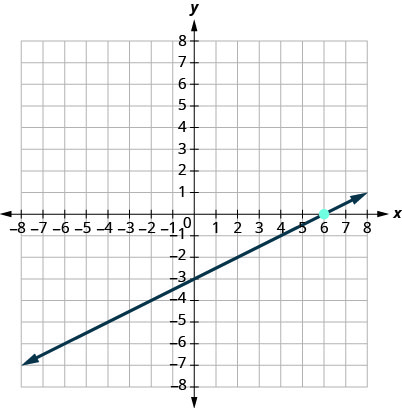
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 3), (2, negative 2), and (6, 0).$

Answer: $y=\frac{1}{2}x−3$

12.
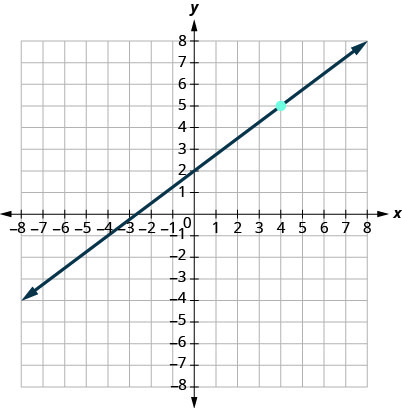
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 2), (4, 5), and (8, 8).$

13.
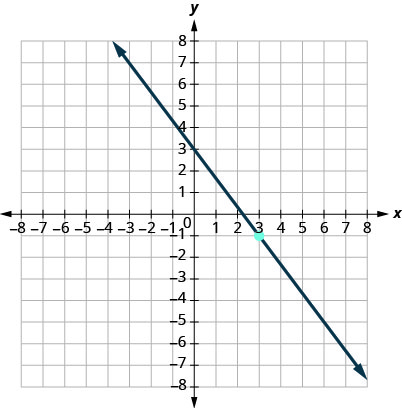
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 3), (3, negative 1), and (6, negative 5).$

Answer: $y=−\frac{4}{3}x+3$

14.
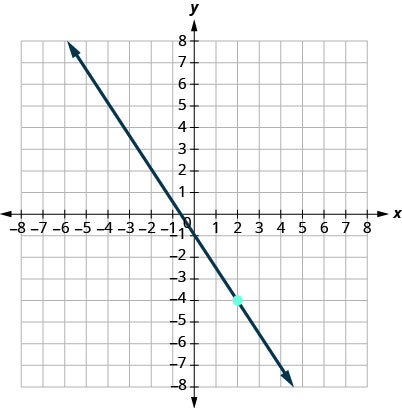
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 1), (2, negative 4), and (4, negative 7).$

15.
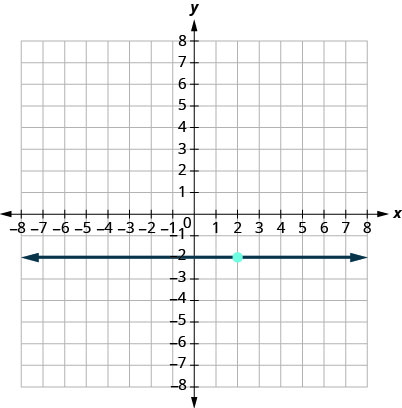
$This figure has a graph of a horizontal straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 2), (1, negative 2), and (2, negative 2).$

Answer: $y=−2$

16.
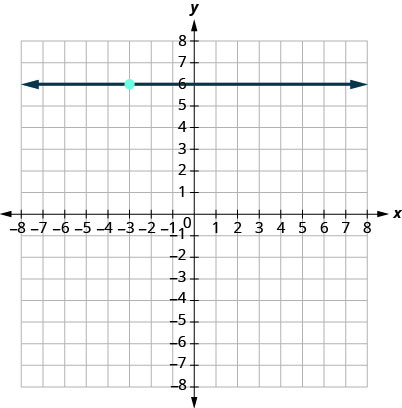
$This figure has a graph of a horizontal straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 6), (1, 6), and (2, 6).$

Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope-intercept form.

17. $m=\frac{5}{8}$, point $(8,3)$

Answer: $y=\frac{5}{8}x−2$

18. $m=\frac{5}{6}$, point $(6,7)$

19. $m=−\frac{3}{5}$, point $(10,−5)$

Answer: $y=−\frac{3}{5}x+1$

20. $m=−\frac{3}{4}$, point $(8,−5)$

21. $m=−\frac{3}{2}$, point $(−4,−3)$

Answer: $y=−\frac{3}{2}x+9$

22. $m=−\frac{5}{2}$, point $(−8,−2)$

23. $m=−7$, point $(−1,−3)$

Answer: $y=−7x−10$

24. $m=−4$, point $(−2,−3)$

25. Horizontal line containing $(−2,5)$

Answer: $y=5$

26. Horizontal line containing $(−2,−3)$

27. Horizontal line containing $(−1,−7)$

Answer: $y=−7$

28. Horizontal line containing $(4,−8)$

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope-intercept form.

29. $(2,6)$ and $(5,3)$

Answer: $y=−x+8$

30. $(4,3)$ and $(8,1)$

31. $(−3,−4)$ and $(5−2)$.

Answer: $y=\frac{1}{4}x−\frac{13}{4}$

32. $(−5,−3)$ and $(4,−6)$.

33. $(−1,3)$ and $(−6,−7)$.

Answer: $y=2x+5$

34. $(−2,8)$ and $(−4,−6)$.

35. $(0,4)$ and $(2,−3)$.

Answer: $y=−\frac{7}{2}x+4$

36. $(0,−2)$ and $(−5,−3)$.

37. $(7,2)$ and $(7,−2)$.

Answer: $x=7$

38. $(−2,1)$ and $(−2,−4)$.

39. $(3,−4)$ and $(5,−4)$.

Answer: $y=−4$

40. $(−6,−3)$ and $(−1,−3)$

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope-intercept form.

41. line $y=4x+2$, point $(1,2)$

Answer: $y=4x−2$

42. line $y=−3x−1$, point $2,−3)$.

43. line $2x−y=6$, point $(3,0)$.

Answer: $y=2x−6$

44. line $2x+3y=6$, point $(0,5)$.

45. line $x=−4$, point $(−3,−5)$.

Answer: $x=−3$

46. line $x−2=0$, point $(1,−2)$

47. line $y=5$, point $(2,−2)$

Answer: $y=−2$

48. line $y+2=0$, point $(3,−3)$

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope-intercept form.

49. line $y=−2x+3$, point $(2,2)$

Answer: $y=\frac{1}{2}x+1$

50. line $y=−x+5$, point $(3,3)$

51. line $y=\frac{3}{4}x−2$, point $(−3,4)$

Answer: $y=−\frac{4}{3}x$

52. line $y=\frac{2}{3}x−4$, point $(2,−4)$

53. line $2x−3y=8$, point $(4,−1)$

Answer: $y=−\frac{3}{2}x+5$

54. line $4x−3y=5$, point $(−3,2)$

55. line $2x+5y=6$, point $(0,0)$

Answer: $y=\frac{5}{2}x$

56. line $4x+5y=−3$, point $(0,0)$

57. line $x=3$, point $(3,4)$

Answer: $y=4$

58. line $x=−5$, point $(1,−2)$

59. line $x=7$, point $(−3,−4)$

Answer: $y=−4$

60. line $x=−1$, point $(−4,0)$

61. line $y−3=0$, point $(−2,−4)$

Answer: $x=−2$

62. line $y−6=0$, point $(−5,−3)$

63. line $y$-axis, point $(3,4)$

Answer: $y=4$

64. line $y$-axis, point $(2,1)$

Mixed Practice

In the following exercises, find the equation of each line. Write the equation in slope-intercept form.

65. Containing the points $(4,3)$ and $(8,1)$

Answer: $y=−\frac{1}{2}x+5$

66. Containing the points $(−2,0)$ and $(−3,−2)$

67. $m=\frac{1}{6}$, containing point $(6,1)$

Answer: $y=\frac{1}{6}x$

68. $m=\frac{5}{6}$, containing point $(6,7)$

69. Parallel to the line $4x+3y=6$, containing point $(0,−3)$

Answer: $y=−\frac{4}{3}x−3$

70. Parallel to the line $2x+3y=6$, containing point $(0,5)$

71. $m=−\frac{3}{4}$, containing point $(8,−5)$

Answer: $y=−\frac{3}{4}x+1$

72. $m=−\frac{3}{5}$, containing point $(10,−5)$

73. Perpendicular to the line $y−1=0$, point $(−2,6)$

Answer: $x=−2$

74. Perpendicular to the line y-axis, point $(−6,2)$

75. Parallel to the line $x=−3$, containing point $(−2,−1)$

Answer: $x=−2$

76. Parallel to the line $x=−4$, containing point $(−3,−5)$

77. Containing the points $(−3,−4)$ and $(2,−5)$

Answer: $y=−\frac{1}{5}x−\frac{23}{5}$

78. Containing the points $(−5,−3)$ and $(4,−6)$

79. Perpendicular to the line $x−2y=5$, point $(−2,2)$

Answer: $y=−2x−2$

80. Perpendicular to the line $4x+3y=1$, point $(0,0)$

Writing Exercises

81. Why are all horizontal lines parallel?

Answer: Answers will vary.

82. Explain in your own words why the slopes of two perpendicular lines must have opposite signs.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$The figure shows a table with six rows and four columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is “confidently”, the third is “with some help”, “no minus I don’t get it!”. Under the first column are the phrases “find the equation of the line given the slope and y-intercept”, “find an equation of the line given the slope and a point”, “find an equation of the line given two points”, “find an equation of a line parallel to a given line”, and “find an equation of a line perpendicular to a given line”. Under the second, third, fourth columns are blank spaces where the learner can check what level of mastery they have achieved.$

b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?