3.5E: Exercises
- Last updated
- Jan 7, 2020
- Save as PDF
- Page ID
- 30832
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Find the Domain and Range of a Relation
In the following exercises, for each relation a. find the domain of the relation b. find the range of the relation.
1. {\{(1,4),(2,8),(3,12),(4,16),(5,20)}\}
- Answer
-
a. {\{1, 2, 3, 4, 5}\} b. {\{4, 8, 12, 16, 20}\}
2. {\{(1,−2),(2,−4),(3,−6),(4,−8),(5,−10)}\}
3. {\{(1,7),(5,3),(7,9),(−2,−3),(−2,8)}\}
- Answer
-
a. {\{1, 5, 7, −2}\} b. {\{7, 3, 9, −3, 8}\}
4. {\{(11,3),(−2,−7),(4,−8),(4,17),(−6,9)}\}
In the following exercises, use the mapping of the relation to a. list the ordered pairs of the relation, b. find the domain of the relation, and c. find the range of the relation.
5.

- Answer
-
a. (Rebecca, January 18), (Jennifer, April 1), (John, January 18), (Hector, June 23), (Luis, February 15), (Ebony, April 7), (Raphael, November 6), (Meredith, August 19), (Karen, August 19), (Joseph, July 30)
b. {Rebecca, Jennifer, John, Hector, Luis, Ebony, Raphael, Meredith, Karen, Joseph}
c. {January 18, April 1, June 23, February 15, April 7, November 6, August 19, July 30}
6.

7. For a woman of height 5'4'' the mapping below shows the corresponding Body Mass Index (BMI). The body mass index is a measurement of body fat based on height and weight. A BMI of 18.5–24.9 is considered healthy.
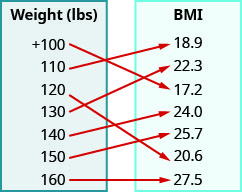
- Answer
-
a. (+100, 17. 2), (110, 18.9), (120, 20.6), (130, 22.3), (140, 24.0), (150, 25.7), (160, 27.5) b. {\{+100, 110, 120, 130, 140, 150, 160,}\} c. {\{17.2, 18.9, 20.6, 22.3, 24.0, 25.7, 27.5}\}
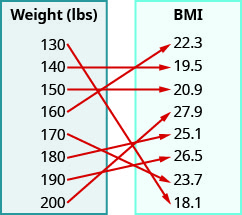
8. For a man of height 5'11'' the mapping below shows the corresponding Body Mass Index (BMI). The body mass index is a measurement of body fat based on height and weight. A BMI of 18.5–24.9 is considered healthy.
In the following exercises, use the graph of the relation to a. list the ordered pairs of the relation b. find the domain of the relation c. find the range of the relation.
9.
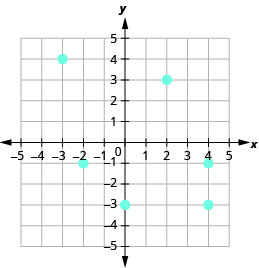
- Answer
-
a. (2, 3), (4, −3), (−2, −1), (−3, 4), (4, −1), (0, −3) b. {\{−3, −2, 0, 2, 4}\}
c. {\{−3, −1, 3, 4}\}
10.
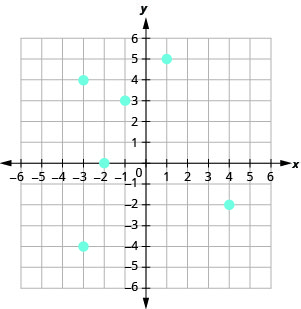
11.
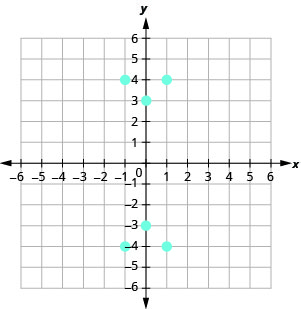
- Answer
-
a. (1, 4), (1, −4), (−1, 4), (−1, −4), (0, 3), (0, −3) b. {\{−1, 0, 1}\} c. {\{−4, −3, 3,4}\}
12.
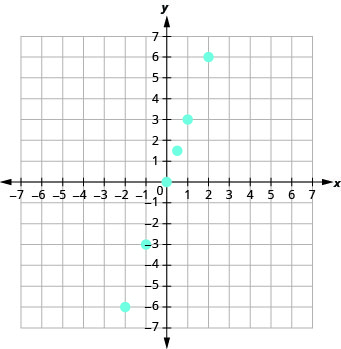
Determine if a Relation is a Function
In the following exercises, use the set of ordered pairs to a. determine whether the relation is a function, b. find the domain of the relation, and c. find the range of the relation.
13. {\{(−3,9),(−2,4),(−1,1), (0,0),(1,1),(2,4),(3,9)}\}
- Answer
-
a. yes b. {\{−3, −2, −1, 0, 1, 2, 3}\} c. {\{9, 4, 1, 0}\}
14. {\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}
15. {\{(−3,27),(−2,8),(−1,1), (0,0),(1,1),(2,8),(3,27)}\}
- Answer
-
a. yes b. {\{−3, −2, −1, 0, 1, 2, 3}\} c. {\{0, 1, 8, 27}\}
16. {\{(−3,−27),(−2,−8),(−1,−1), (0,0),(1,1),(2,8),(3,27)}\}
In the following exercises, use the mapping to a. determine whether the relation is a function, b. find the domain of the function, and c. find the range of the function.
17.
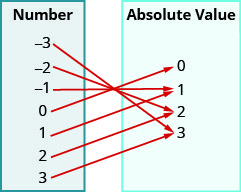
- Answer
-
a. yes b. {\{−3, −2, −1, 0, 1, 2, 3}\} c. {\{0, 1, 2, 3}\}
18.
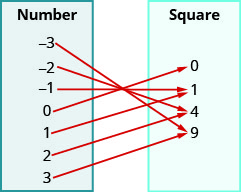
19.

- Answer
-
a. no b. {Jenny, R and y, Dennis, Emily, Raul} c. {RHern and ez@state.edu, JKim@gmail.com, Raul@gmail.com, ESmith@state.edu, DBroen@aol.com, jenny@aol.cvom, R and y@gmail.com}
20.

In the following exercises, determine whether each equation is a function.
21. a. 2x+y=−3
b. y=x^2
c. x+y^2=−5
- Answer
-
a. yes b. yes c. no
22. a. y=3x−5
b. y=x^3
c. 2x+y^2=4
23. a. y−3x^3=2
b. x+y^2=3
c. 3x−2y=6
- Answer
-
a. yes b. no c. yes
24. a. 2x−4y=8
b. −4=x^2−y
c. y^2=−x+5
Find the Value of a Function
In the following exercises, evaluate the function: a. f(2) b. f(−1) c. f(a).
25. f(x)=5x−3
- Answer
-
a. f(2)=7 b. f(−1)=−8 c. f(a)=5a−3
26. f(x)=3x+4
27. f(x)=−4x+2
- Answer
-
a. f(2)=−6 b. f(−1)=6 c. f(a)=−4a+2
28. f(x)=−6x−3
29. f(x)=x^2−x+3
- Answer
-
a. f(2)=5 b. f(−1)=5
c. f(a)=a^2−a+3
30. f(x)=x^2+x−2
31. f(x)=2x^2−x+3
- Answer
-
a. f(2)=9 b. f(−1)=6
c. f(a)=2a^2−a+3
32. f(x)=3x^2+x−2
In the following exercises, evaluate the function: a. g(h^2) b. g(x+2) c. g(x)+g(2).
33. g(x)=2x+1
- Answer
-
a. g(h^2)=2h^2+1
b. g(x+2)=4x+5
c. g(x)+g(2)=2x+6
34. g(x)=5x−8
35. g(x)=−3x−2
- Answer
-
a. g(h^2)=−3h^2−2
b. g(x+2)=−3x−8
c. g(x)+g(2)=−3x−10
36. g(x)=−8x+2
37. g(x)=3−x
- Answer
-
a. g(h^2)=3−h^2
b. g(x+2)=1−x
c. g(x)+g(2)=4−x
38. g(x)=7−5x
In the following exercises, evaluate the function.
39. f(x)=3x^2−5x; f(2)
- Answer
-
2
40. g(x)=4x^2−3x; g(3)
41. F(x)=2x^2−3x+1; F(−1)
- Answer
-
6
42. G(x)=3x^2−5x+2; G(−2)
43. h(t)=2|t−5|+4; f(−4)
- Answer
-
22
44. h(y)=3|y−1|−3; h(−4)
45. f(x)=x+2x−1; f(2)
- Answer
-
4
46. g(x)=x−2x+2; g(4)
In the following exercises, solve.
47. The number of unwatched shows in Sylvia’s DVR is 85. This number grows by 20 unwatched shows per week. The function N(t)=85+20t represents the relation between the number of unwatched shows, N, and the time, t, measured in weeks.
a. Determine the independent and dependent variable.
b. Find N(4). Explain what this result means
- Answer
-
a. t IND; N DEP
b. N(4)=165 the number of unwatched shows in Sylvia’s DVR at the fourth week.
48. Every day a new puzzle is downloaded into Ken’s account. Right now he has 43 puzzles in his account. The function N(t)=43+t represents the relation between the number of puzzles, N, and the time, t, measured in days.
a. Determine the independent and dependent variable.
b. Find N(30). Explain what this result means.
49. The daily cost to the printing company to print a book is modeled by the function C(x)=3.25x+1500 where C is the total daily cost and x is the number of books printed.
a. Determine the independent and dependent variable.
b. Find N(0). Explain what this result means.
c. Find N(1000). Explain what this result means.
- Answer
-
a. x IND; C DEP
b. N(0)=1500 the daily cost if no books are printed
c. N(1000)=4750 the daily cost of printing 1000 books
50. The daily cost to the manufacturing company is modeled by the function C(x)=7.25x+2500 where C(x) is the total daily cost and x is the number of items manufactured.
a. Determine the independent and dependent variable.
b. Find C(0). Explain what this result means.
c. Find C(1000). Explain what this result means.
Writing Exercises
51. In your own words, explain the difference between a relation and a function.
52. In your own words, explain what is meant by domain and range.
53. Is every relation a function? Is every function a relation?
54. How do you find the value of a function?
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


