4.3E: Exercises
- Page ID
- 30843
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Solve Mixture Applications
In the following exercises, translate to a system of equations and solve.
1. Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?
2. Tickets for the Cirque du Soleil show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?
- Answer
-
110 adult tickets, 190 child tickets
3. Tickets for an Amtrak train cost $10 for children and $22 for adults. Josie paid $1200 for a total of 72 tickets. How many children tickets and how many adult tickets did Josie buy?
4. Tickets for a Minnesota Twins baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?
- Answer
-
6 good seats, 10 cheap seats
5. Tickets for a dance recital cost $15 for adults and $7 dollars for children. The dance company sold 253 tickets and the total receipts were $2771. How many adult tickets and how many child tickets were sold?
6. Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2204. How many adult tickets and how many child tickets were sold?
- Answer
-
92 adult tickets, 220 children tickets
7. Brandon has a cup of quarters and dimes with a total value of $3.80. The number of quarters is four less than twice the number of quarters. How many quarters and how many dimes does Brandon have?
8. Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.95. The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?
- Answer
-
13 nickels, 3 dimes
9. Peter has been saving his loose change for several days. When he counted his quarters and nickels, he found they had a total value $13.10. The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?
10. Lucinda had a pocketful of dimes and quarters with a value of $6.20. The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?
- Answer
-
42 dimes, 8 quarters
11. A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?
12. A cashier has 54 bills, all of which are $10 or $20 bills. The total value of the money is $910. How many of each type of bill does the cashier have?
- Answer
-
17 $10 bills, 37 $20 bills
13. Marissa wants to blend candy selling for $1.80 per pound with candy costing $1.20 per pound to get a mixture that costs her $1.40 per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?
14. How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?
- Answer
-
80 pounds nuts and 40 pounds raisins
15. Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $1.79 per gallon and the cost of the fruit drink is $2.49 per gallon. Hannah’s budget requires that the punch cost $2.21 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?
16. Joseph would like to make twelve pounds of a coffee blend at a cost of $6 per pound. He blends Ground Chicory at $5 a pound with Jamaican Blue Mountain at $9 per pound. How much of each type of coffee should he use?
- Answer
-
9 pounds of Chicory coffee, 3 pounds of Jamaican Blue Mountain coffee
17. Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a twenty-pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?
18. Twelve-year old Melody wants to sell bags of mixed candy at her lemonade stand. She will mix M&M’s that cost $4.89 per bag and Reese’s Pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of M&M’s and how many bags of Reese’s Pieces should she use?
- Answer
-
10 bags of M&M’s, 15 bags of Reese’s Pieces
19. Jotham needs 70 liters of a 50% solution of an alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?
20. Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?
- Answer
-
7.5 liters of each solution
21. A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?
22. A scientist needs 120 milliliters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?
- Answer
-
80 liters of the 25% solution and 40 liters of the 10% solution
23. A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?
24. A 90% antifreeze solution is to be mixed with a 75% antifreeze solution to get 360 liters of an 85% solution. How many liters of the 90% and how many liters of the 75% solutions will be used?
- Answer
-
240 liters of the 90% solution and 120 liters of the 75% solution
Solve Interest Applications
In the following exercises, translate to a system of equations and solve.
25. Hattie had $3000 to invest and wants to earn 10.6% interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?
26. Carol invested $2560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25% interest on the total investment. How much money did she put in each account?
- Answer
-
$1600 at 8%, 960 at 6%
27. Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4000 in interest in one year?
28. Arnold invested $64,000, some at 5.5% interest and the rest at 9%. How much did he invest at each rate if he received $4500 in interest in one year?
- Answer
-
$28,000 at 9%, $36,000 at 5.5%
29. After four years in college, Josie owes $65, 800 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owes for one year was $2878.50. What is the amount of each loan?
30. Mark wants to invest $10,000 to pay for his daughter’s wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1095 in interest in one year?
- Answer
-
$8500 CD, $1500 savings account
31. A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn 5.25% interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?
32. A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5% This year, the business expects to pay $4,650 in interest on the two loans. How much is each loan?
- Answer
-
$55,000 on loan at 6% and $30,000 on loan at 4.5%
Solve Applications of Cost and Revenue Functions
33. The manufacturer of an energy drink spends $1.20 to make each drink and sells them for $2. The manufacturer also has fixed costs each month of $8,000.
ⓐ Find the cost function C when x energy drinks are manufactured.
ⓑ Find the revenue function R when x drinks are sold.
ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.
ⓓ Find the break-even point. Interpret what the break-even point means.
34. The manufacturer of a water bottle spends $5 to build each bottle and sells them for $10. The manufacturer also has fixed costs each month of $6500. ⓐ Find the cost function C when x bottles are manufactured. ⓑ Find the revenue function R when x bottles are sold. ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid. ⓓ Find the break-even point. Interpret what the break-even point means.
- Answer
-
ⓐ C(x)=5x+6500
ⓑ R(x)=10x
ⓒ
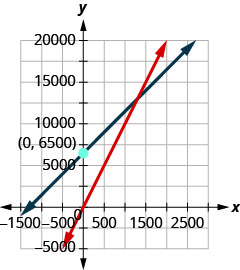
ⓓ 1,500; when 1,500 water bottles are sold, the cost and the revenue equal $15,000
Writing Exercises
35. Take a handful of two types of coins, and write a problem similar to Example relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.
36. In Example, we used elimination to solve the system of equations
{s+b=40,0000.08s+0.03b=0.071(40,000).
Could you have used substitution or elimination to solve this system? Why?
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?


