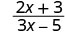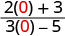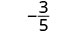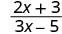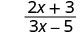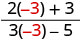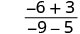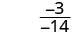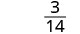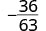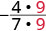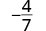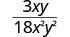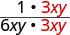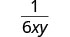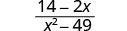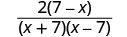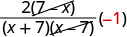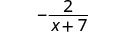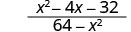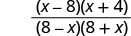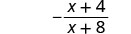7.1: Simplify Rational Expressions
- Page ID
- 30949
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Summary
By the end of this section, you will be able to:- Determine the values for which a rational expression is undefined
- Evaluate rational expressions
- Simplify rational expressions
- Simplify rational expressions with opposite factors
Are you Ready?
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
In Chapter 1, we reviewed the properties of fractions and their operations. We introduced rational numbers, which are just fractions where the numerators and denominators are integers, and the denominator is not zero.
In this chapter, we will work with fractions whose numerators and denominators are polynomials. We call these rational expressions.
Definition: RATIONAL EXPRESSION
A rational expression is an expression of the form \(\frac{p(x)}{q(x)}\), where p and q are polynomials and \(q \ne 0\).
Here are some examples of rational expressions:
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
Notice that the first rational expression listed above, \(−\frac{13}{42}\), is just a fraction. Since a constant is a polynomial with degree zero, the ratio of two constants is a rational expression, provided the denominator is not zero.
We will perform same operations with rational expressions that we do with fractions. We will simplify, add, subtract, multiply, divide, and use them in applications.
Determine the Values for Which a Rational Expression is Undefined
When we work with a numerical fraction, it is easy to avoid dividing by zero, because we can see the number in the denominator. In order to avoid dividing by zero in a rational expression, we must not allow values of the variable that will make the denominator be zero.
If the denominator is zero, the rational expression is undefined. The numerator of a rational expression may be 0—but not the denominator.
So before we begin any operation with a rational expression, we examine it first to find the values that would make the denominator zero. That way, when we solve a rational equation for example, we will know whether the algebraic solutions we find are allowed or not.
- Set the denominator equal to zero.
- Solve the equation in the set of reals, if possible.
Determine the values for which the rational expression is undefined:
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
Solution
The expression will be undefined when the denominator is zero.
| 1. | \(\frac{9y}{x}\) |
| Set the denominator equal to zero. Solve for the variable. | x=0 |
| \(\frac{9y}{x}\) is undefined for x=0. | |
| 2. |
\(\frac{4b−3}{2b+5}\) |
| Set the denominator equal to zero. Solve for the variable. | 2b+5=0 |
| 2b=−5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\) is undefined for \(b=−\frac{5}{2}\). | |
| 3. | \(\frac{x+4}{x^2+5x+6x}\) |
| Set the denominator equal to zero. Solve for the variable. | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| x+2=0 or x+3=0 | |
| x=−2 or x=−3 | |
| \(\frac{x+4}{x^2+5x+6x}\) is undefined for x=−2 or x=−3. |
Saying that the rational expression \(\frac{x+4}{x^2+5x+6x}\) is undefined for x=−2orx=−3 is similar to writing the phrase “void where prohibited” in contest rules.
Try It \(\PageIndex{2}\)
Determine the values for which the rational expression is undefined:
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
Determine the values for which the rational expression is undefined:
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- Answer
-
- q=0
- \(y=−\frac{2}{3}\)
- m=2, m=−3
Evaluate Rational Expressions
To evaluate a rational expression, we substitute values of the variables into the expression and simplify, just as we have for many other expressions in this book.
Evaluate \(\frac{2x+3}{3x−5}\) for each value:
- x=0
- x=2
- x=−3
Solution
| 1. |  |
 |
 |
| Simplify. |  |
| 2. |  |
 |
 |
| Simplify. |  |
 |
|
 |
|
| 3. |  |
 |
 |
| Simplify. |  |
 |
|
 |
Try It \(\PageIndex{5}\)
Evaluate \(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Simplify Rational Expressions
Just like a fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator, a rational expression is simplified if it has no common factors, other than 1, in its numerator and denominator.
A rational expression is considered simplified if there are no common factors in its numerator and denominator.
For example:
- \(\frac{2}{3}\) is simplified because there are no common factors of 2 and 3.
- \(\frac{2x}{3x}\) is not simplified because x is a common factor of 2x and 3x.
We use the Equivalent Fractions Property to simplify numerical fractions. We restate it here as we will also use it to simplify rational expressions.
If a, b, and c are numbers where \(b \ne 0\), \(c\ne 0\), then \(\frac{a}{b}=\frac{a·c}{b·c}\) and \(\frac{a·c}{b·c}=\frac{a}{b}\)
Notice that in the Equivalent Fractions Property, the values that would make the denominators zero are specifically disallowed. We see \(b \ne 0\), \(c\ne 0\) clearly stated. Every time we write a rational expression, we should make a similar statement disallowing values that would make a denominator zero. However, to let us focus on the work at hand, we will omit writing it in the examples.
Let’s start by reviewing how we simplify numerical fractions.
Simplify: \(−\frac{36}{63}\).
Solution
 |
|
| Rewrite the numerator and denominator showing the common factors. |  |
| Simplify using the Equivalent Fractions Property. |  |
Notice that the fraction \(−\frac{4}{7}\) is simplified because there are no more common factors.
Try It \(\PageIndex{14}\)
Simplify: \(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
Simplify: \(−\frac{42}{54}\).
- Answer
-
\(−\frac{7}{9}\)
Throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example, \(x \ne 0\) and \(y \ne 0\).
Simplify: \(\frac{3xy}{18x^{2}y^{2}}\).
Solution
 |
|
| Rewrite the numerator and denominator showing the common factors. |  |
| Simplify using the Equivalent Fractions Property. |  |
Did you notice that these are the same steps we took when we divided monomials in Polynomials?
Try It \(\PageIndex{17}\)
Simplify: \(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
Simplify: \(\frac{16x^{2}y}{2xy^2}\).
- Answer
-
\(\frac{8x}{y}\)
Be very careful as you remove common factors. Factors are multiplied to make a product. You can remove a factor from a product. You cannot remove a term from a sum.
Note that removing the x’s from \(\frac{x+5}{x}\) would be like cancelling the 2’s in the fraction \(\frac{2+5}{2}\)!
How to Simplify Rational Binomials
Simplify: \(\frac{2x+8}{5x+20}\).
Solution
Try It \(\PageIndex{20}\)
Simplify: \(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
Simplify: \(\frac{7y+35}{5y+25}\).
- Answer
-
\(\frac{7}{5}\)
We now summarize the steps you should follow to simplify rational expressions.
- Factor the numerator and denominator completely.
- Simplify by dividing out common factors.
We’ll use the methods we covered in Factoring to factor the polynomials in the numerators and denominators in the following examples.
Simplify: \(\frac{x^2+5x+6}{x^2+8x+12}\).
Solution
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| Factor the numerator and denominator. | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| Remove the common factor x+2 from the numerator and the denominator. | \(\frac{x+3}{x+6}\) |
Can you tell which values of x must be excluded in this example?
Try It \(\PageIndex{23}\)
Simplify: \(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
Simplify: \(\frac{x^2−3x−10}{x^2+x−2}\).
- Answer
-
\(\frac{x−5}{x−1}\)
Simplify: \(\frac{y^2+y−42}{y^2−36}\).
Solution
| \(\frac{y^2+y−42}{y^2−36}\). | |
| Factor the numerator and denominator. | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| Remove the common factor y−6 from the numerator and the denominator. | \(\frac{y+7}{y+6}\) |
Try It \(\PageIndex{26}\)
Simplify: \(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
Simplify: \(\frac{x^2+8x+7}{x^2−49}\).
- Answer
-
\(\frac{x+1}{x−7}\)
Simplify: \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\).
Solution
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| Factor the numerator and denominator, using grouping to factor the numerator. | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| Remove the common factor p−2 from the numerator and the denominator. | \(\frac{p^2+2}{p−5}\) |
Try It \(\PageIndex{29}\)
Simplify: \(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
Simplify: \(\frac{p^3−p^2+2p−2}{p^2+4p−5}\).
- Answer
-
\(\frac{p^2+2}{p+5}\)
Simplify: \(\frac{2n^2−14n}{4n^2−16n−48}\).
Solution
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| Factor the numerator and denominator, first factoring out the GCF. | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| Remove the common factor, 2. | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
Try It \(\PageIndex{32}\)
Simplify: \(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
Simplify: \(\frac{4x^2−16x}{8x^2−16x−64}\).
- Answer
-
\(\frac{x}{2(x+2)}\)
Simplify: \(\frac{3b^2−12b+12}{6b^2−24}\).
Solution
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| Factor the numerator and denominator, first factoring out the GCF. | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| Remove the common factors of b−2 and 3. | \(\frac{3(b−2)}{2(b+2)}\) |
Try It \(\PageIndex{35}\)
Simplify: \(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
Simplify: \(\frac{5y^2−30y+25}{2y^2−50}\).
- Answer
-
\(\frac{5(x−1)}{2(x+5)}\)
Simplify: \(\frac{m^3+8}{m^2−4}\).
Solution
| \(\frac{m^3+8}{m^2−4}\) | |
| Factor the numerator and denominator, using the formulas for sum of cubes and difference of squares. | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| Remove the common factors of m+2. | \(\frac{m^2−2m+4}{m−2}\) |
Try It \(\PageIndex{38}\)
Simplify: \(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
Simplify: \(\frac{x^3+8}{x^2−4}\).
- Answer
-
\(\frac{x^2−2x+4}{x−2}\)
How to Simplify Rational Binomials
Simplify: \(\frac{2x+8}{5x+20}\).
Solution
Simplify Rational Expressions with Opposite Factors
Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. Let’s start with a numerical fraction, say \(\frac{7}{−7}\).
We know this fraction simplifies to −1. We also recognize that the numerator and denominator are opposites.
In Foundations, we introduced opposite notation: the opposite of a is −a. We remember, too, that −a=−1·a
We simplify the fraction \(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
So, in the same way, we can simplify the fraction \(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
But the opposite of x−3 could be written differently:
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
This means the fraction \(\frac{x−3}{3−x}\) simplifies to −1.
In general, we could write the opposite of a−b as b−a. So the rational expression \(\frac{a−b}{b−a}\) simplifies to −1.
The opposite of a−b is b−a
\(\frac{a−b}{b−a}=−1\), \(a \ne b\)
An expression and its opposite divide to −1
We will use this property to simplify rational expressions that contain opposites in their numerators and denominators.
Simplify: \(\frac{x−8}{8−x}\).
Solution
| \(\frac{x−8}{8−x}\). | |
| Recognize that x−8 and 8−x are opposites | −1 |
Try It \(\PageIndex{41}\)
Simplify: \(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
Simplify: \(\frac{n−9}{9−n}\).
- Answer
-
−1
Remember, the first step in simplifying a rational expression is to factor the numerator and denominator completely.
Simplify: \(\frac{14−2x}{x^2−49}\).
Solution
 |
|
| Factor the numerator and denominator. |  |
| Recognize 7−x and x−7 are opposites. |  |
| Simplify. |  |
Try It \(\PageIndex{44}\)
Simplify: \(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
Simplify: \(\frac{3y−27}{81−y^2}\).
- Answer
-
\(−\frac{3}{9+y}\)
Simplify: \(\frac{x^2−4x−32}{64−x^2}\).
Solution
 |
|
| Factor the numerator and denominator. |  |
| Recognize the factors that are opposites. |  |
| Simplify. |  |
Try It \(\PageIndex{47}\)
Simplify: \(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
Simplify: \(\frac{x^2+x−2}{1−x^2}\).
- Answer
-
\(−\frac{x+2}{x+1}\)
Key Concepts
- Determine the Values for Which a Rational Expression is Undefined
- Set the denominator equal to zero.
- Solve the equation, if possible.
- Simplified Rational Expression
- A rational expression is considered simplified if there are no common factors in its numerator and denominator.
- Simplify a Rational Expression
- Factor the numerator and denominator completely.
- Simplify by dividing out common factors.
- Opposites in a Rational Expression
- The opposite of a−b is b−a
\(\frac{a−b}{b−a}=−1\) \(a \ne b\), \(b \ne 0\), \(a \ne b\)
- The opposite of a−b is b−a
Glossary
- rational expression
- A rational expression is an expression of the form \(\frac{p}{q}\), where p and q are polynomials and \(q \ne 0\).