7.3: Add and Subtract Rational Expressions
- Last updated
- Save as PDF
- Page ID
- 30875
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Summary
By the end of this section, you will be able to:
- Add and subtract rational expressions with a common denominator
- Add and subtract rational expressions whose denominators are opposites
- Find the least common denominator of rational expressions
- Add and subtract rational expressions with unlike denominators
- Add and subtract rational functions
Before you get started, take this readiness quiz.
Add and Subtract Rational Expressions with a Common Denominator
What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.
It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.
RATIONAL EXPRESSION ADDITION AND SUBTRACTION
If \(p\), \(q\), and \(r\) are polynomials where \(r\neq 0\), then
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
To add or subtract rational expressions with a common denominator, add or subtract the numerators and place the result over the common denominator.
We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.
Remember, too, we do not allow values that would make the denominator zero. What value of \(x\) should be excluded in the next example?
Example \(\PageIndex{1}\)
Add: \(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\).
Solution
Since the denominator is \(x+4\), we must exclude the value \(x=−4\).
\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)
The expression simplifies to \(x+7\) but the original expression had a denominator of \(x+4\) so \(x\neq −4\).
Try It \(\PageIndex{2}\)
Simplify: \(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\).
- Answer
-
\(x+2\)
Try It \(\PageIndex{3}\)
Simplify: \(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\).
- Answer
-
\(x+3\)
To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator. Be careful of the signs when you subtract a binomial or trinomial.
Example \(\PageIndex{4}\)
Subtract: \(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\).
Solution
\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)
Try It \(\PageIndex{5}\)
Subtract: \(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\).
- Answer
-
\(\dfrac{x−11}{x−2}\)
Try It \(\PageIndex{6}\)
Subtract: \(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\).
- Answer
-
\(\dfrac{x−3}{x+9}\)
Add and Subtract Rational Expressions Whose Denominators are Opposites
When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by \(\dfrac{−1}{−1}\).
Let’s see how this works.
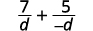 |
|
| Multiply the second fraction by \(\dfrac{−1}{−1}\). | 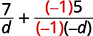 |
| The denominators are the same. | 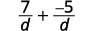 |
| Simplify. | 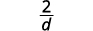 |
Be careful with the signs as you work with the opposites when the fractions are being subtracted.
Example \(\PageIndex{7}\)
Subtract: \(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\).
Solution
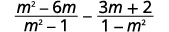 |
|
|
The denominators are opposites, so multiply the |
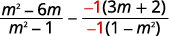 |
| Simplify the second fraction. | 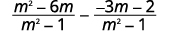 |
| The denominators are the same. Subtract the numerators. | 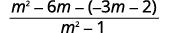 |
| Distribute. | 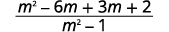 |
| Combine like terms. | 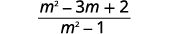 |
| Factor the numerator and denominator. | 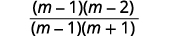 |
| Simplify by removing common factors. | 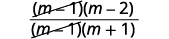 |
| Simplify. | 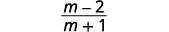 |
Try It \(\PageIndex{8}\)
Subtract: \(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\).
- Answer
-
\(\dfrac{y+3}{y+2}\)
Try It \(\PageIndex{9}\)
Subtract: \(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\).
- Answer
-
\(\dfrac{3n−2}{n−1}\)
Find the Least Common Denominator of Rational Expressions
When we add or subtract rational expressions with unlike denominators, we will need to get common denominators. If we review the procedure we used with numerical fractions, we will know what to do with rational expressions.
Let’s look at this example: \(\dfrac{7}{12}+\dfrac{5}{18}\). Since the denominators are not the same, the first step was to find the least common denominator (LCD).
To find the LCD of the fractions, we factored 12 and 18 into primes, lining up any common primes in columns. Then we “brought down” one prime from each column. Finally, we multiplied the factors to find the LCD.
When we add numerical fractions, once we found the LCD, we rewrote each fraction as an equivalent fraction with the LCD by multiplying the numerator and denominator by the same number. We are now ready to add.
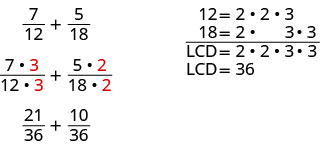
We do the same thing for rational expressions. However, we leave the LCD in factored form.
FIND THE LEAST COMMON DENOMINATOR OF RATIONAL EXPRESSIONS.
- Factor each denominator completely.
- List the factors of each denominator. Match factors vertically when possible.
- Bring down the columns by including all factors, but do not include common factors twice.
- Write the LCD as the product of the factors.
Remember, we always exclude values that would make the denominator zero. What values of xx should we exclude in this next example?
Example \(\PageIndex{10}\)
a. Find the LCD for the expressions \(\dfrac{8}{x^2−2x−3}\), \(\dfrac{3x}{x^2+4x+3}\) and b. rewrite them as equivalent rational expressions with the lowest common denominator.
Solution
a.
| Find the LCD for \(\dfrac{8}{x^2−2x−3}\), \(\dfrac{3x}{x^2+4x+3}\). | |
| Factor each denominator completely, lining up common factors. Bring down the columns. |
 |
| Write the LCD as the product of the factors. | 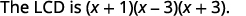 |
b.
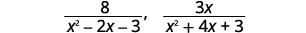 |
|
| Factor each denominator. | 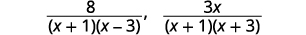 |
| Multiply each denominator by the ‘missing’ LCD factor and multiply each numerator by the same factor. |
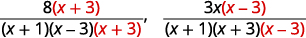 |
| Simplify the numerators. | 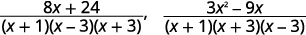 |
Try It \(\PageIndex{11}\)
a. Find the LCD for the expressions \(\dfrac{2}{x^2−x−12}\), \(\dfrac{1}{x^2−16}\) b. rewrite them as equivalent rational expressions with the lowest common denominator.
- Answer
-
a. \((x−4)(x+3)(x+4)\)
b. \(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)
Try It \(\PageIndex{12}\)
a. Find the LCD for the expressions \(\dfrac{3x}{x^2−3x+10}\), \(\dfrac{5}{x^2+3x+2}\) b. rewrite them as equivalent rational expressions with the lowest common denominator.
- Answer
-
a. \((x+2)(x−5)(x+1)\)
b. \(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\),
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)
Add and Subtract Rational Expressions with Unlike Denominators
Now we have all the steps we need to add or subtract rational expressions with unlike denominators.
Example \(\PageIndex{13}\): How to Add Rational Expressions with Unlike Denominators
Add: \(\dfrac{3}{x−3}+\dfrac{2}{x−2}\).
Solution



Try It \(\PageIndex{14}\)
Add: \(\dfrac{2}{x−2}+\dfrac{5}{x+3}\).
- Answer
-
\(\dfrac{7x−4}{(x−2)(x+3)}\)
Try It \(\PageIndex{15}\)
Add: \(\dfrac{4}{m+3}+\dfrac{3}{m+4}\).
- Answer
-
\(\dfrac{7m+25}{(m+3)(m+4)}\)
The steps used to add rational expressions are summarized here.
ADD OR SUBTRACT RATIONAL EXPRESSIONS.
- Determine if the expressions have a common denominator.
- Yes – go to step 2.
- No – Rewrite each rational expression with the LCD.
- Find the LCD.
- Rewrite each rational expression as an equivalent rational expression with the LCD.
- Add or subtract the rational expressions.
- Simplify, if possible.
Avoid the temptation to simplify too soon. In the example above, we must leave the first rational expression as \(\dfrac{3x−6}{(x−3)(x−2)}\) to be able to add it to \(\dfrac{2x−6}{(x−2)(x−3)}\). Simplify only after you have combined the numerators.
Example \(\PageIndex{16}\)
Add: \(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\).
Solution
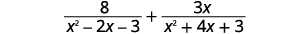 |
|
| Do the expressions have a common denominator? | No. |
| Rewrite each expression with the LCD. | |
| \(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \) | |
| Rewrite each rational expression as an equivalent rational expression with the LCD. |
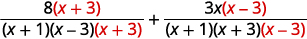 |
| Simplify the numerators. | 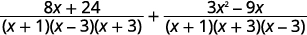 |
| Add the rational expressions. | 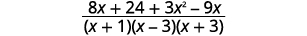 |
| Simplify the numerator. | 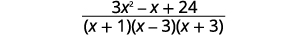 |
| The numerator is prime, so there are no common factors. |
Try It \(\PageIndex{17}\)
Add: \(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\).
- Answer
-
\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)
Try It \(\PageIndex{18}\)
Add: \(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\).
- Answer
-
\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)
The process we use to subtract rational expressions with different denominators is the same as for addition. We just have to be very careful of the signs when subtracting the numerators.
Example \(\PageIndex{19}\)
Subtract: \(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\).
Solution
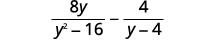 |
|
| Do the expressions have a common denominator? | No. |
| Rewrite each expression with the LCD. | |
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \) | |
| Rewrite each rational expression as an equivalent rational expression with the LCD. |
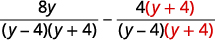 |
| Simplify the numerators. | 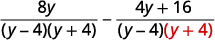 |
| Subtract the rational expressions. | 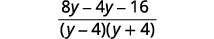 |
| Simplify the numerator. | 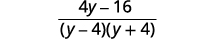 |
| Factor the numerator to look for common factors. | 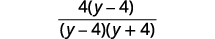 |
| Remove common factors | 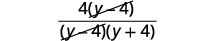 |
| Simplify. | 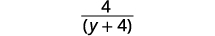 |
Try It \(\PageIndex{20}\)
Subtract: \(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\).
- Answer
-
\(\dfrac{1}{x−2}\)
Try It \(\PageIndex{21}\)
Subtract: \(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\).
- Answer
-
\(\dfrac{−3}{z−3}\)
There are lots of negative signs in the next example. Be extra careful.
Example \(\PageIndex{22}\)
Subtract: \(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\).
Solution
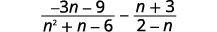 |
|
| Factor the denominator. | 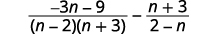 |
| Since \(n−2\) and \(2−n\) are opposites, we will multiply the second rational expression by \(\dfrac{−1}{−1}\). |
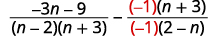 |
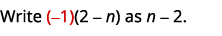 |
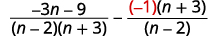 |
| Simplify. Remember, \(a−(−b)=a+b\). | 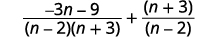 |
| Do the rational expressions have a common denominator? No. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \) | |
| Rewrite each rational expression as an equivalent rational expression with the LCD. |
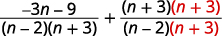 |
| Simplify the numerators. | 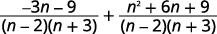 |
| Add the rational expressions. | 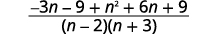 |
| Simplify the numerator. | 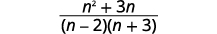 |
| Factor the numerator to look for common factors. | 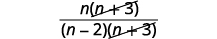 |
| Simplify. | 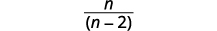 |
Try It \(\PageIndex{23}\)
Subtract: \(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\).
- Answer
-
\(\dfrac{5x+1}{(x−6)(x+1)}\)
Try It \(\PageIndex{24}\)
Subtract: \(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\).
- Answer
-
\(\dfrac{y+3}{y+4}\)
Things can get very messy when both fractions must be multiplied by a binomial to get the common denominator.
Example \(\PageIndex{25}\)
Subtract: \(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\).
Solution
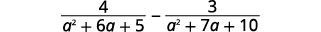 |
|
| Factor the denominators. | 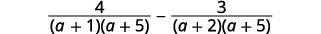 |
| Do the rational expressions have a common denominator? No. |
|
|
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \) |
|
| Rewrite each rational expression as an equivalent rational expression with the LCD. |
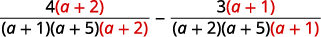 |
| Simplify the numerators. | 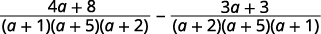 |
| Subtract the rational expressions. |  |
| Simplify the numerator. | 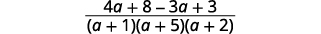 |
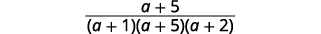 |
|
| Look for common factors. | 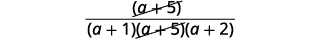 |
| Simplify. | 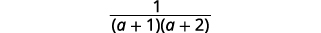 |
Try It \(\PageIndex{26}\)
Subtract: \(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\).
- Answer
-
\(\dfrac{1}{(b+1)(b−1)}\)
Try It \(\PageIndex{27}\)
Subtract: \(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\).
- Answer
-
\(\dfrac{1}{(x+2)(x+1)}\)
We follow the same steps as before to find the LCD when we have more than two rational expressions. In the next example, we will start by factoring all three denominators to find their LCD.
Example \(\PageIndex{28}\)
Simplify: \(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\).
Solution
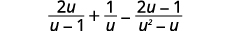 |
|
| Do the expressions have a common denominator? No. Rewrite each expression with the LCD. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\) | |
| Rewrite each rational expression as an equivalent rational expression with the LCD. |
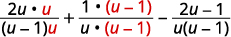 |
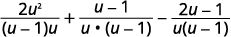 |
|
| Write as one rational expression. | 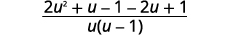 |
| Simplify. | 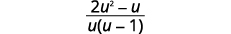 |
| Factor the numerator, and remove common factors. |
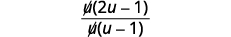 |
| Simplify. | 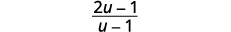 |
Try It \(\PageIndex{29}\)
Simplify: \(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\).
- Answer
-
\(\dfrac{v+3}{v+1}\)
Try It \(\PageIndex{30}\)
Simplify: \(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\).
- Answer
-
\(\dfrac{3w}{w+7}\)
Add and subtract rational functions
To add or subtract rational functions, we use the same techniques we used to add or subtract polynomial functions.
Example \(\PageIndex{31}\)
Find \(R(x)=f(x)−g(x)\) where \(f(x)=\dfrac{x+5}{x−2}\) and \(g(x)=\dfrac{5x+18}{x^2−4}\).
- xolution
-

Substitute in the functions \(f(x)\), \(g(x)\). 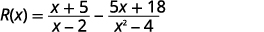
Factor the denominators. 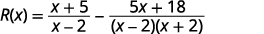
Do the expressions have a common denominator? No.
Rewrite each expression with the LCD.\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\) Rewrite each rational expression as an
equivalent rational expression with the LCD.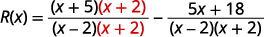
Write as one rational expression. 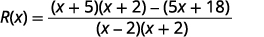
Simplify. 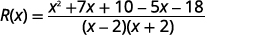
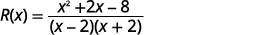
Factor the numerator, and remove
common factors.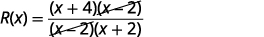
Simplify. 
Try It \(\PageIndex{32}\)
Find \(R(x)=f(x)−g(x)\) where \(f(x)=\dfrac{x+1}{x+3}\) and \(g(x)=\dfrac{x+17}{x^2−x−12}\).
- Answer
-
\(\dfrac{x−7}{x−4}\)
Try It \(\PageIndex{33}\)
Find \(R(x)=f(x)+g(x)\) where \(f(x)=\dfrac{x−4}{x+3}\) and \(g(x)=\dfrac{4x+6}{x^2−9}\).
- Answer
-
\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)
Access this online resource for additional instruction and practice with adding and subtracting rational expressions.
- Add and Subtract Rational Expressions- Unlike Denominators
Key Concepts
- Rational Expression Addition and Subtraction
If \(p\), \(q\), and \(r\) are polynomials where \(r\neq 0\), then
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\] - How to find the least common denominator of rational expressions.
- Factor each expression completely.
- List the factors of each expression. Match factors vertically when possible.
- Bring down the columns.
- Write the LCD as the product of the factors.
- How to add or subtract rational expressions.
- Determine if the expressions have a common denominator.
- Yes – go to step 2.
- No – Rewrite each rational expression with the LCD.
- Find the LCD.
- Rewrite each rational expression as an equivalent rational expression with the LCD.
- Add or subtract the rational expressions.
- Simplify, if possible.
- Determine if the expressions have a common denominator.


