7.6: Solve Uniform Motion and Work Applications

Last updated
Save as PDF

Page ID: 30946

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Solve uniform motion applications
Solve work applications

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

An express train and a local bus leave Chicago to travel to Champaign. The express bus can make the trip in 2 hours and the local bus takes 5 hours for the trip. The speed of the express bus is 42 miles per hour faster than the speed of the local bus. Find the speed of the local bus.
If you missed this problem, review [link].
Solve $\frac{1}{3}x+\frac{1}{4}x=\frac{5}{6}$.
If you missed this problem, review [link].
Solve: $18t^2−30=−33t$.
If you missed this problem, review [link].

Solve Uniform Motion Applications

We have solved uniform motion problems using the formula D=rt in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

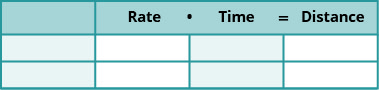
$The above image is a table with 4 columns and three rows. The first row is the header row. The second column in the header row has the word “rate”. The third column has the word, “Time”. The fourth column says “Distance”. The rest of the spaces are blank.$

The formula D=rt assumes we know r and t and use them to find D. If we know D and r and need to find t, we would solve the equation for t and get the formula $t=\frac{D}{r}$

We have also explained how flying with or against a current affects the speed of a vehicle. We will revisit that idea in the next example.

Example $\PageIndex{1}$

An airplane can fly 200 miles into a 30 mph headwind in the same amount of time it takes to fly 300 miles with a 30 mph tailwind. What is the speed of the airplane?

Solution

This is a uniform motion situation. A diagram will help us visualize the situation.

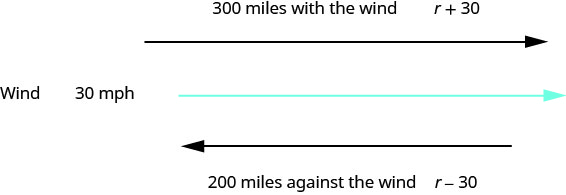
$The above image has two parallel arrows. The first arrow has its tip pointing to the right The words,”300 miles with the wind r plus 30” above the arrow tip. Below that is a squiggly line. To the left of the squiggly line it says, “Wind 30 miles per hour”. Below that is an arrow with its tip pointing to the left. Below that are the words, “200 miles against the wind r minus 30”.$

We fill in the chart to organize the information.

We are looking for the speed of the airplane.	Let r= the speed of the airplane.
When the plane flies with the wind, the wind increases its speed and the rate is r+30.
When the plane flies against the wind, the wind decreases its speed and the rate is r−30.
Write in the rates. Write in the distances. Since D=r∙t , we solve for t and get $\frac{D}{r}$. We divide the distance by the rate in each row, and place the expression in the time column.	$.$
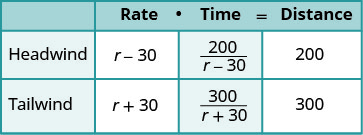We know the times are equal and so we write our equation.	$\frac{200}{r−30}=\frac{300}{r+30}$
We multiply both sides by the LCD. 200(r+30)=300(r−30)
Simplify.	(r+30)(200)=(r−30)(300)
	200r+6000=300r−9000
Solve.	15000=100r 150=r
Check.
Is 150 mph a reasonable speed for an airplane? Yes. If the plane is traveling 150 mph and the wind is 30 mph:
Tailwind 150+30=180 mph $\frac{300}{180}=\frac{5}{3}$ hours
Headwind 150−30=120 mph $\frac{200}{120}=\frac{5}{3}$ hours
The times are equal, so it checks.	The plane was traveling 150 mph.

Try It $\PageIndex{2}$

Link can ride his bike 20 miles into a 3 mph headwind in the same amount of time he can ride 30 miles with a 3 mph tailwind. What is Link’s biking speed?

Answer: 15 mph

Try It $\PageIndex{3}$

Judy can sail her boat 5 miles into a 7 mph headwind in the same amount of time she can sail 12 miles with a 7 mph tailwind. What is the speed of Judy’s boat without a wind?

Answer: 17 mph

In the next example, we will know the total time resulting from travelling different distances at different speeds.

Example $\PageIndex{4}$

Jazmine trained for 3 hours on Saturday. She ran 8 miles and then biked 24 miles. Her biking speed is 4 mph faster than her running speed. What is her running speed?

Solution

This is a uniform motion situation. A diagram will help us visualize the situation.

$The above image is a straight line with two arrow heads pointing to the right. At the far left, above the line, it reads, “run” and further down, slightly past the first arrow head, it reads, “bike”. Slightly below the line, to the far left, before the first arrow head, it reads, “8 miles” and to the far right, after the first arrow head it reads, “12 miles”. The region from the far left to the far right of the arrow is grouped to indicate the entire length of the line is 3 hours.$

We fill in the chart to organize the information.

We are looking for Jazmine’s running speed.	Let r= Jazmine’s running sp
Her biking speed is 4 miles faster than her running speed.	r+4= her biking speed
The distances are given, enter them into the chart.
Since D=r∙t , we solve for t and get $t=\frac{D}{r}$ We divide the distance by the rate in each row, and place the expression in the time column.	$.$
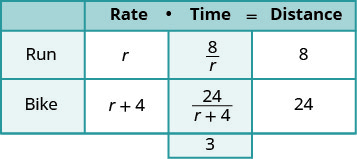Write a word sentence.	Her time plus the time biking
Translate the sentence to get the equation.	$\frac{8}{r}+\frac{24}{r+4}=3$
Solve.	$r(r+4)(\frac{8}{r}+\frac{24}{r+4})=3r(r+4)$ $8(r+4)+24r=3r^2+12r$ $8r+32+24r=3r^2+12r$ $32+32r=3r^2+12r$ $0=3r^2−20r−32$ $0=(3r+4)(r−8)$
	(3r+4)=0, (r−8)=0
	$r=−\frac{4}{3}$, r=8
Check. r=8
A negative speed does not make sense in this problem, so r=8 is the solution.
Is 8 mph a reasonable running speed? Yes.
Run 8 mph, $\frac{8 miles}{8 mph}=1 hour$ Bike 12 mph, $\frac{24 miles}{12 mph}=2 hours$ Total 3 hours. Jazmine’s running speed is 8 mph.

Try It $\PageIndex{5}$

Dennis went cross-country skiing for 6 hours on Saturday. He skied 20 mile uphill and then 20 miles back downhill, returning to his starting point. His uphill speed was 5 mph slower than his downhill speed. What was Dennis’ speed going uphill and his speed going downhill?

Answer: 10 mph

Try It $\PageIndex{6}$

Tony drove 4 hours to his home, driving 208 miles on the interstate and 40 miles on country roads. If he drove 15 mph faster on the interstate than on the country roads, what was his rate on the country roads?

Answer: 50 mph

Once again, we will use the uniform motion formula solved for the variable t.

Example $\PageIndex{7}$

Hamilton rode his bike downhill 12 miles on the river trail from his house to the ocean and then rode uphill to return home. His uphill speed was 8 miles per hour slower than his downhill speed. It took him 2 hours longer to get home than it took him to get to the ocean. Find Hamilton’s downhill speed.

Solution

This is a uniform motion situation. A diagram will help us visualize the situation.

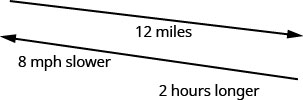
$The above figure show 2 diagonal, parallel lines pointing in opposite directions. The top line points to the right, and downward and has “12 miles” written beneath it. The bottom line points to the left and upward, and has, “ 8 miles per hour slower, 2 hours longer” written beneath it.$

We fill in the chart to organize the information.

We are looking for Hamilton’s downhill speed.	Let r= Hamilton’s downhill speed.
His uphill speed is 8 miles per hour slower. Enter the rates into the chart.	h−8= Hamilton’s uphill speed
The distance is the same in both directions, 12 miles. Since D=r∙t , we solve for t and get $t=\frac{D}{r}$ We divide the distance by the rate in each row, and place the expression in the time column.	$.$
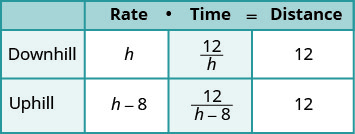Write a word sentence about the time.	He took 2 hours longer uphill than downhill. The uphill time is 2 more than the downhill time.
Translate the sentence to get the equation. Solve.	$\frac{12}{h−8}=\frac{12}{h}+2$ $h(h−8)(\frac{12}{h−8})=h(h−8)(\frac{12}{h}+2)$ 12h=12(h−8)+2h(h−8) $12h=12h−96+2h^2−16h$ $0=2h^2−16h−96$ $0=2(h^2−8h−48)$ 0=2(h−12)(h+4) h−12=0, h+4=0 h=12, h=−4
Check. Is 12 mph a reasonable speed for biking downhill? Yes.
Downhill 12 mph, $\frac{12 miles}{12 mph}=1 hour$
Uphill 12−8=4 mph $\frac{12 miles}{4 mph}=3 hours$
	The uphill time is 2 hours more than the downhill time. Hamilton’s downhill speed is 12 mph.

Try It $\PageIndex{8}$

Kayla rode her bike 75 miles home from college one weekend and then rode the bus back to college. It took her 2 hours less to ride back to college on the bus than it took her to ride home on her bike, and the average speed of the bus was 10 miles per hour faster than Kayla’s biking speed. Find Kayla’s biking speed.

Answer: 15 mph

Try It $\PageIndex{9}$

Victoria jogs 12 miles to the park along a flat trail and then returns by jogging on an 18 mile hilly trail. She jogs 1 mile per hour slower on the hilly trail than on the flat trail, and her return trip takes her two hours longer. Find her rate of jogging on the flat trail.

Answer: 6 mph

Solve Work Applications

Suppose Pete can paint a room in 10 hours. If he works at a steady pace, in 1 hour he would paint $\frac{1}{10}$ of the room. If Alicia would take 8 hours to paint the same room, then in 1 hour she would paint $\frac{1}{8}$ of the room. How long would it take Pete and Alicia to paint the room if they worked together (and didn’t interfere with each other’s progress)?

This is a typical ‘work’ application. There are three quantities involved here – the time it would take each of the two people to do the job alone and the time it would take for them to do the job together.

Let’s get back to Pete and Alicia painting the room. We will let t be the number of hours it would take them to paint the room together. So in 1 hour working together they have completed $\frac{1}{t}$ of the job.

In one hour Pete did $\frac{1}{10}$ of the job. Alicia did $\frac{1}{8}$ of the job. And together they did $\frac{1}{t}$ of the job.

We can model this with the word equation and then translate to a rational equation. To find the time it would take them if they worked together, we solve for t.

	$.$
	$.$
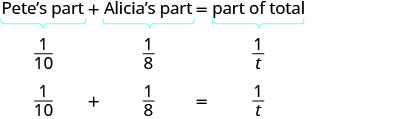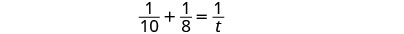Multiply by the LCD, 40t	$.$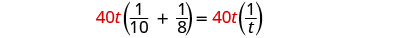
Distribute.	$.$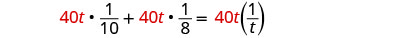
Simplify and solve.	$.$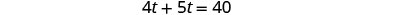
	$.$
	$.$
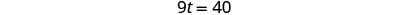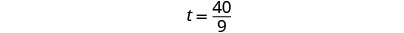We’ll write as a mixed number so that we can convert it to hours and minutes.	$.$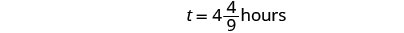
Remember, 1 hour = 60 minutes.	$.$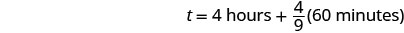
Multiply, and then round to the nearest minute.	$.$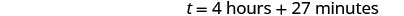
	It would take Pete and Alica about 4 hours and 27 minutes to paint the room.

Keep in mind, it should take less time for two people to complete a job working together than for either person to do it alone.

Example $\PageIndex{10}$

The weekly gossip magazine has a big story about the Princess’ baby and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes 6 hours to do the job and Press #2 takes 12 hours to do the job. How long will it take the printer to get the magazine printed with both presses running together?

Solution

This is a work problem. A chart will help us organize the information.

Let t= the number of hours needed to complete the job together.
Enter the hours per job for Press #1, Press #2 and when they work together. If a job on Press #1 takes 6 hours, then in 1 hour $\frac{1}{6}$ of the job is completed. Similarly find the part of the job completed/hours for Press #2 and when they both work together.	$.$
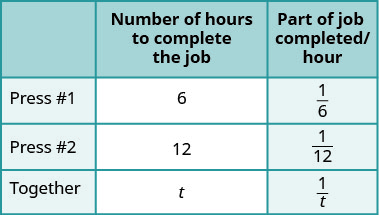Write a word sentence.
The part completed by Press #1 plus the part completed by Press #2 equals the amount completed together.
Translate to an equation.	$.$
Solve.	$.$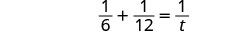
Multiply by the LCD, 12t.	$.$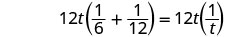
Simplify.	$.$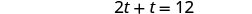
	$.$
	$.$
	When both presses are running it takes 4 hours to do the job.

Try It $\PageIndex{11}$

One gardener can mow a golf course in 4 hours, while another gardener can mow the same golf course in 6 hours. How long would it take if the two gardeners worked together to mow the golf course?

Answer: 2 hours and 24 minutes

Try It $\PageIndex{12}$

Carrie can weed the garden in 7 hours, while her mother can do it in 3. How long will it take the two of them working together?

Answer: 2 hours and 6 minutes

Example $\PageIndex{13}$

Corey can shovel all the snow from the sidewalk and driveway in 4 hours. If he and his twin Casey work together, they can finish shoveling the snow in 2 hours. How many hours would it take Casey to do the job by himself?

Solution

This is a work application. A chart will help us organize the information.
We are looking for how many hours it would take Casey to complete the job by himself.
Let t= the number of hours needed for Casey to complete.
Enter the hours per job for Corey, Casey, and when they work together. If Corey takes 4 hours, then in 1 hour $\frac{1}{4}$ of the job is completed. Similarly find the part of the job completed/hours for Casey and when they both work together.	$.$
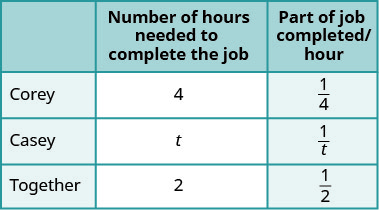Write a word sentence.
The part completed by Corey plus the part completed by Casey equals the amount completed together.
Translate to an equation:	$.$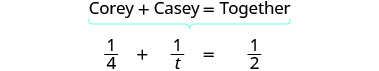
Solve.	$.$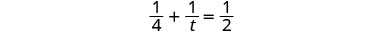
Multiply by the LCD, 4t.	$.$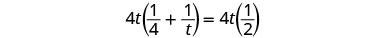
Simplify.	$.$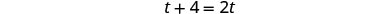
	$.$
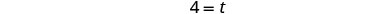	It would take Casey 4 hours to do the job alone.

Try It $\PageIndex{14}$

Two hoses can fill a swimming pool in 10 hours. It would take one hose 26 hours to fill the pool by itself. How long would it take for the other hose, working alone, to fill the pool?

Answer: 16.25 hours

Try It $\PageIndex{15}$

Cara and Cindy, working together, can rake the yard in 4 hours. Working alone, it takes Cindy 6 hours to rake the yard. How long would it take Cara to rake the yard alone?

Answer: 12 hours