Chapter Review Exercises
Simplify Rational Expressions
Determine the Values for Which a Rational Expression is Undefined
In the following exercises, determine the values for which the rational expression is undefined.
Exercise \(\PageIndex{1}\)
\(\dfrac{2a+1}{3a−2}\)
- Answer
-
\(a \ne \dfrac{2}{3}\)
Exercise \(\PageIndex{2}\)
\(\dfrac{b−3}{b^2−16}\)
Exercise \(\PageIndex{3}\)
\(\dfrac{3xy^2}{5y}\)
- Answer
-
\(y \ne 0\)
Exercise \(\PageIndex{4}\)
\(\dfrac{u−3}{u^2−u−30}\)
Evaluate Rational Expressions
In the following exercises, evaluate the rational expressions for the given values.
Exercise \(\PageIndex{5}\)
\(\dfrac{4p−1}{p^2+5}\) when \(p=−1\)
- Answer
-
\(−\dfrac{5}{6}\)
Exercise \(\PageIndex{6}\)
\(\dfrac{q^2−5}{q+3}\) when \(q=7\)
Exercise \(\PageIndex{7}\)
\(\dfrac{y^2−8}{y^2−y−2}\) when \(y=1\)
- Answer
-
\(\dfrac{7}{2}\)
Example \(\PageIndex{8}\)
\(\dfrac{z^2+2}{4z−z^2}\) when \(z=3\)
In the following exercises, simplify.
Exercise \(\PageIndex{9}\)
\(\dfrac{10}{24}\)
- Answer
-
\(\dfrac{5}{12}\)
Exercise \(\PageIndex{10}\)
\(\dfrac{8m^4}{16mn^3}\)
Exercise \(\PageIndex{11}\)
\(\dfrac{14a−14}{a−1}\)
- Answer
-
\(14\)
Exercise \(\PageIndex{12}\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
Simplify Rational Expressions with Opposite Factors
In the following exercises, simplify.
Exercise \(\PageIndex{13}\)
\(\dfrac{c^2−c−2}{4−c^2}\)
- Answer
-
\(-\dfrac{c+1}{c+2}\)
Exercise \(\PageIndex{14}\)
\(\dfrac{d−16}{16−d}\)
Exercise \(\PageIndex{15}\)
\(\dfrac{7v−35}{25−v^2}\)
- Answer
-
\(−\dfrac{7}{5+v}\)
Exercise \(\PageIndex{16}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
Multiply and Divide Rational Expressions
Multiply Rational Expressions
In the following exercises, multiply.
Exercise \(\PageIndex{17}\)
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- Answer
-
\(\dfrac{1}{20}\)
Exercise \(\PageIndex{18}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
Exercise \(\PageIndex{19}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- Answer
-
\(\dfrac{3}{b}\)
Exercise \(\PageIndex{20}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
Divide Rational Expressions
In the following exercises, divide.
Exercise \(\PageIndex{21}\)
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- Answer
-
\(\dfrac{6t}{(t+6)^2}\)
Exercise \(\PageIndex{22}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
Exercise \(\PageIndex{23}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- Answer
-
\(\dfrac{1}{11+w}\)
Exercise \(\PageIndex{24}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
Exercise \(\PageIndex{25}\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- Answer
-
\(5c+4\)
Exercise \(\PageIndex{26}\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
Add and Subtract Rational Expressions with a Common Denominator
Add Rational Expressions with a Common Denominator
In the following exercises, add.
Exercise \(\PageIndex{27}\)
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- Answer
-
\(1\)
Exercise \(\PageIndex{28}\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
Exercise \(\PageIndex{29}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- Answer
-
\(p+5\)
Exercise \(\PageIndex{30}\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
Subtract Rational Expressions with a Common Denominator
In the following exercises, subtract.
Exercise \(\PageIndex{31}\)
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- Answer
-
\(d-7\)
Exercise \(\PageIndex{32}\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
Exercise \(\PageIndex{33}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- Answer
-
\(\dfrac{q−3}{q+5}\)
Exercise \(\PageIndex{34}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
In the following exercises, add and subtract.
Exercise \(\PageIndex{35}\)
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- Answer
-
\(\dfrac{15w+2}{6w−1}\)
Exercise \(\PageIndex{36}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
Exercise \(\PageIndex{37}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- Answer
-
\(\dfrac{3b−2}{b+7}\)
Exercise \(\PageIndex{38}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
Add and Subtract Rational Expressions With Unlike Denominators
Find the Least Common Denominator of Rational Expressions
In the following exercises, find the LCD.
Exercise \(\PageIndex{38}\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- Answer
-
\((m+2)(m−5)(m+4)\)
Exercise \(\PageIndex{39}\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
Exercise \(\PageIndex{40}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- Answer
-
\((3p+1)(p+6)(p+8)\)
In the following exercises, rewrite as equivalent rational expressions with the given denominator.
Exercise \(\PageIndex{41}\)
Rewrite as equivalent rational expressions with denominator \((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\).
Exercise \(\PageIndex{42}\)
Rewrite as equivalent rational expressions with denominator \((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\).
- Answer
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
Exercise \(\PageIndex{43}\)
Rewrite as equivalent rational expressions with denominator \((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
Add Rational Expressions with Different Denominators
In the following exercises, add.
Exercise \(\PageIndex{44}\)
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- Answer
-
\(\dfrac{19}{15}\)
Exercise \(\PageIndex{45}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
Exercise \(\PageIndex{46}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- Answer
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
Exercise \(\PageIndex{47}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
Exercise \(\PageIndex{48}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- Answer
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
Exercise \(\PageIndex{49}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
In the following exercises, subtract and add.
Exercise \(\PageIndex{50}\)
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- Answer
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
Exercise \(\PageIndex{51}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
Exercise \(\PageIndex{52}\)
\(\dfrac{7m+3}{m+2}−5\)
- Answer
-
\(\dfrac{2m−7}{m+2}\)
Exercise \(\PageIndex{53}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
Exercise \(\PageIndex{54}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- Answer
-
\(4d−8\)
Exercise \(\PageIndex{55}\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
Simplify Complex Rational Expressions
Simplify a Complex Rational Expression by Writing it as Division
In the following exercises, simplify.
Exercise \(\PageIndex{56}\)
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- Answer
-
\(\dfrac{a−2}{2a}\)
Exercise \(\PageIndex{57}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
Exercise \(\PageIndex{58}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- Answer
-
\(\dfrac{(x−8)(x−5)}{2}\)
Exercise \(\PageIndex{59}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
Simplify a Complex Rational Expression by Using the LCD
In the following exercises, simplify.
Exercise \(\PageIndex{60}\)
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- Answer
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
Exercise \(\PageIndex{61}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
Exercise \(\PageIndex{62}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- Answer
-
\(\dfrac{z−5}{21z+21}\)
Exercise \(\PageIndex{63}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
Solve Rational Equations
Solve Rational Equations
In the following exercises, solve.
Exercise \(\PageIndex{64}\)
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- Answer
-
\(\dfrac{6}{7}\)
Exercise \(\PageIndex{65}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
Exercise \(\PageIndex{66}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- Answer
-
\(\dfrac{3}{2}\)
Exercise \(\PageIndex{67}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
Exercise \(\PageIndex{68}\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- Answer
-
no solution
Exercise \(\PageIndex{69}\)
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
Solve a Rational Equation for a Specific Variable
In the following exercises, solve for the indicated variable.
Exercise \(\PageIndex{70}\)
\(\dfrac{V}{l}=hw\) for \(l\)
- Answer
-
\(l=\dfrac{V}{hw}\)
Exercise \(\PageIndex{71}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\) for \(y\)
Exercise \(\PageIndex{72}\)
\(x=\dfrac{y+5}{z−7}\) for \(z\)
- Answer
-
\(z=\dfrac{y+5+7x}{x}\)
Exercise \(\PageIndex{73}\)
\(P=\dfrac{k}{V}\) for \(V\)
Solve Proportions
In the following exercises, solve.
Exercise \(\PageIndex{74}\)
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- Answer
-
\(\dfrac{12}{5}\)
Exercise \(\PageIndex{75}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
Exercise \(\PageIndex{76}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- Answer
-
\(15\)
Exercise \(\PageIndex{77}\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
In the following exercises, solve using proportions.
Exercise \(\PageIndex{78}\)
Rachael had a \(21\) ounce strawberry shake that has \(739\) calories. How many calories are there in a \(32\) ounce shake?
- Answer
-
\(1161\) calories
Exercise \(\PageIndex{79}\)
Leo went to Mexico over Christmas break and changed \($525\) dollars into Mexican pesos. At that time, the exchange rate had \($1\) US is equal to \(16.25\) Mexican pesos. How many Mexican pesos did he get for his trip?
Solve Similar Figure Applications
In the following exercises, solve.
Exercise \(\PageIndex{80}\)
\(∆ABC\) is similar to \(∆XYZ\). The lengths of two sides of each triangle are given in the figure. Find the lengths of the third sides.
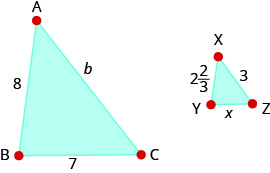
- Answer
-
\(b=9\); \(x=2\dfrac{1}{3}\)
Exercise \(\PageIndex{81}\)
On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the figure below. If the actual distance from Rome to Vienna is \(700\) miles, find the distance from
- a. Paris to Rome
- b. Paris to Vienna
-
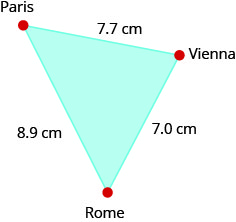
Exercise \(\PageIndex{82}\)
Tony is \(5.75\) feet tall. Late one afternoon, his shadow was \(8\) feet long. At the same time, the shadow of a nearby tree was \(32\) feet long. Find the height of the tree.
- Answer
-
\(23\) feet
Exercise \(\PageIndex{83}\)
The height of a lighthouse in Pensacola, Florida is \(150\) feet. Standing next to the statue, \(5.5\) foot tall Natalie cast a \(1.1\) foot shadow How long would the shadow of the lighthouse be?
Solve Uniform Motion Applications
In the following exercises, solve.
Exercise \(\PageIndex{84}\)
When making the 5-hour drive home from visiting her parents, Lisa ran into bad weather. She was able to drive \(176\) miles while the weather was good, but then driving \(10\) mph slower, went \(81\) miles in the bad weather. How fast did she drive when the weather was bad?
- Answer
-
45 mph
Exercise \(\PageIndex{85}\)
Mark is riding on a plane that can fly \(490\) miles with a tailwind of \(20\) mph in the same time that it can fly \(350\) miles against a tailwind of \(20\) mph. What is the speed of the plane?
Exercise \(\PageIndex{86}\)
John can ride his bicycle \(8\) mph faster than Luke can ride his bike. It takes Luke \(3\) hours longer than John to ride \(48\) miles. How fast can John ride his bike?
- Answer
-
\(16\) mph
Exercise \(\PageIndex{87}\)
Mark was training for a triathlon. He ran \(8\) kilometers and biked \(32\) kilometers in a total of \(3\) hours. His running speed was \(8\) kilometers per hour less than his biking speed. What was his running speed?
Solve Work Applications
In the following exercises, solve.
Exercise \(\PageIndex{88}\)
Jerry can frame a room in \(1\) hour, while Jake takes \(4\) hours. How long could they frame a room working together?
- Answer
-
\(\dfrac{4}{5}\) hour
Exercise \(\PageIndex{89}\)
Lisa takes \(3\) hours to mow the lawn while her cousin, Barb, takes \(2\) hours. How long will it take them working together?
Exercise \(\PageIndex{90}\)
Jeffrey can paint a house in \(6\) days, but if he gets a helper he can do it in \(4\) days. How long would it take the helper to paint the house alone?
- Answer
-
\(12\) days
Exercise \(\PageIndex{91}\)
Sue and Deb work together writing a book that takes them \(90\) days. If Sue worked alone it would take her \(120\) days. How long would it take Deb to write the book alone?
Use Direct and Inverse Variation
Solve Direct Variation Problems
In the following exercises, solve.
Exercise \(\PageIndex{92}\)
If \(y\) varies directly as \(x\), when \(y=9\) and \(x=3\), find \(x\) when \(y=21\).
- Answer
-
\(7\)
Exercise \(\PageIndex{93}\)
If \(y\) varies directly as \(x\), when \(y=20\) and \(x=2\), find \(y\) when \(x=4\).
Exercise \(\PageIndex{94}\)
If \(m\) varies inversely with the square of \(n\), when \(m=4\) and \(n=6\), find \(m\) when \(n=2\).
- Answer
-
\(36\)
Exercise \(\PageIndex{95}\)
Vanessa is traveling to see her fiancé. The distance, \(d\), varies directly with the speed, \(v\), she drives. If she travels \(258\) miles driving \(60\) mph, how far would she travel going \(70\) mph?
Exercise \(\PageIndex{96}\)
If the cost of a pizza varies directly with its diameter, and if an \(8\)” diameter pizza costs \($12\), how much would a \(6\)” diameter pizza cost?
- Answer
-
\($9\)
Exercise \(\PageIndex{97}\)
The distance to stop a car varies directly with the square of its speed. It takes \(200\) feet to stop a car going \(50\) mph. How many feet would it take to stop a car going \(60\) mph?
Solve Inverse Variation Problems
In the following exercises, solve.
Exercise \(\PageIndex{98}\)
The number of tickets for a music fundraiser varies inversely with the price of the tickets. If Madelyn has just enough money to purchase \(12\) tickets for \($6\), how many tickets can Madelyn afford to buy if the price increased to \($8\)?
- Answer
-
\(97\) tickets
Exercise \(\PageIndex{99}\)
On a string instrument, the length of a string varies inversely with the frequency of its vibrations. If an \(11\)-inch string on a violin has a frequency of \(360\) cycles per second, what frequency does a \(12\)-inch string have?
Practice Test
In the following exercises, simplify.
Exercise \(\PageIndex{1}\)
\(\dfrac{3a^{2}b}{6ab^2}\)
- Answer
-
\(\dfrac{a}{2b}\)
Exercise \(\PageIndex{2}\)
\(\dfrac{5b−25}{b^2−25}\)
In the following exercises, perform the indicated operation and simplify.
Exercise \(\PageIndex{3}\)
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- Answer
-
\(\dfrac{x+3}{3x}\)
Exercise \(\PageIndex{4}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
Exercise \(\PageIndex{5}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- Answer
-
\(\dfrac{4+5q}{pq}\)
Exercise \(\PageIndex{6}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
Exercise \(\PageIndex{7}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- Answer
-
\(\dfrac{19}{16}\)
Exercise \(\PageIndex{8}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
In the following exercises, solve each equation.
Exercise \(\PageIndex{9}\)
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- Answer
-
\(x = \dfrac{14}{11}\)
Exercise \(\PageIndex{10}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
Exercise \(\PageIndex{11}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- Answer
-
\(z = \dfrac{1}{2}\)
Exercise \(\PageIndex{12}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
Exercise \(\PageIndex{13}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- Answer
-
\(r = 4\)
In the following exercises, solve.
Exercise \(\PageIndex{14}\)
If \(y\) varies directly with \(x\), and \(x=5\) when \(y=30\), find \(x\) when \(y=42\).
Exercise \(\PageIndex{15}\)
If \(y\) varies inversely with \(x\) and \(x=6\) when \(y=20\), find \(y\) when \(x=2\).
- Answer
-
\(y=60\)
Exercise \(\PageIndex{16}\)
If \(y\) varies inversely with the square of \(x\) and \(x=3\) when \(y=9\), find \(y\) when \(x=4\).
Exercise \(\PageIndex{17}\)
The recommended erythromycin dosage for dogs, is \(5\) mg for every pound the dog weighs. If Daisy weighs \(25\) pounds, how many milligrams of erythromycin should her veterinarian prescribe?
- Answer
-
\(125\) mg
Exercise \(\PageIndex{18}\)
Julia spent \(4\) hours Sunday afternoon exercising at the gym. She ran on the treadmill for \(10\) miles and then biked for \(20\) miles. Her biking speed was \(5\) mph faster than her running speed on the treadmill. What was her running speed?
Exercise \(\PageIndex{19}\)
Kurt can ride his bike for \(30\) miles with the wind in the same amount of time that he can go \(21\) miles against the wind. If the wind’s speed is \(6\) mph, what is Kurt’s speed on his bike?
- Answer
-
\(14\) mph
Exercise \(\PageIndex{20}\)
Amanda jogs to the park \(8\) miles using one route and then returns via a \(14\)-mile route. The return trip takes her \(1\) hour longer than her jog to the park. Find her jogging rate.
Exercise \(\PageIndex{21}\)
An experienced window washer can wash all the windows in Mike’s house in \(2\) hours, while a new trainee can wash all the windows in \(7\) hours. How long would it take them working together?
- Answer
-
\(1\frac{5}{9}\) hour
Exercise \(\PageIndex{22}\)
Josh can split a truckload of logs in \(8\) hours, but working with his dad they can get it done in \(3\) hours. How long would it take Josh’s dad working alone to split the logs?
Exercise \(\PageIndex{23}\)
The price that Tyler pays for gas varies directly with the number of gallons he buys. If \(24\) gallons cost him \($59.76\), what would \(30\) gallons cost?
- Answer
-
\($74.70\)
Exercise \(\PageIndex{24}\)
The volume of a gas in a container varies inversely with the pressure on the gas. If a container of nitrogen has a volume of \(29.5\) liters with \(2000\) psi, what is the volume if the tank has a \(14.7\) psi rating? Round to the nearest whole number.
Exercise \(\PageIndex{25}\)
The cities of Dayton, Columbus, and Cincinnati form a triangle in southern Ohio, as shown on the figure below, that gives the map distances between these cities in inches.
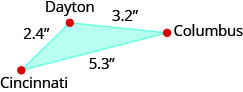
The actual distance from Dayton to Cincinnati is \(48\) miles. What is the actual distance between Dayton and Columbus?
- Answer
-
\(64\) miles





