Part 2: Analyze and Interpret Data
- Page ID
- 10300
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)I. Measures of Central Tendency (measures that give us some indication of the overall "average" of the data)
- Mode: In a list of numbers, the number that occurs most frequently.
- Median: After you rank order the data, if you have an odd number of data values then the median of the data values is the middle data value of the list. If you have an even number of data values, then the median is the average of the two middle data values.
- Mean: You find the mean by summing all the data values and dividing by the number of data values you have.
1. Click on this link to see a video finding the mean, median and mode of some data.
2. Practice problems. There may be a problem on your exam from these practice problems.
3. Watch this video to find out how to find a missing data value given the mean.
4. Practice problems find the missing value given the mean.
Check in question 1. (10 points)
Find the median, mean and mode for the following data:
\(7,4,1,9,3,8,3,5,10,3, 7, 8\)
Check in question 2. (5 points)
Given the following data:
School district 1 number of snow days 7
School district 2 number of snow days 6
School district 3 number of snow days 4
School district 4 number of snow days 8
School district 5 number of snow days?
If the mean is 7.4 snow days find the number of snow days in school district 5.
Check in question 3. (5 points)
In a class of 24 students if the mean on a 100 point test was 77, is it possible that 18 students got a score of 55 or below? Please give a reason for your answer.
II. Measures of dispersion and position: These measures give an indication of how the data is distributed. Is the data spread out? Is the data bunched together?
A. Range: The difference between the largest and smallest data values.
B. Standard deviation: The square root of the variance.
1. Find the mean.( \(\large{\bar {x}}\))
2. For each data value (\(\large x\)), find the difference between the number and the mean.
3. Square the differences that you found in step 2.
4. Divide by \(n\) (the number of data values you have)
This will be your variance. Now take the square root of it.
Note: We are dividing by n because we are working with a population. We would divide by \(n-1\) if we were working with a sample.
Note: We will be using \(n\) and not \(n-1\) in our calculations.
1. Click on this link to watch a video finding the range and the standard deviation.
2. Click on this link to see another example of finding the variance and standard deviation.
https://www.mathsisfun.com/data/standard-deviation.html
Note: In general the greater the standard deviation the more spread out your data is.
Example: \(2, 3, 4, 5, 6\)
Find the standard deviation.
The mean is \(\large \bar x = \frac{2 + 3 + 4 + 5 + 6}{5} = \frac{20}{5} = 4\)
(2-4)^2 + (3-4)^2 +(4-4)^2 +(5-4)^2 + (6 – 4)^2 =
(-2)^2 + (-1)^2 + (0)^2 + (1)^2 + (2)^2
= 4+1+0+1+4
=10
So then we divide this sum by \(n\).
\(\frac{10}{5} =2\) This is our variance.
To find the standard deviation, take the square root of 2.
Check in question 4.
Find the range, variance, and standard deviation for the following data. (10 points)
72 80 83 90 97 100
Round your answer to two decimal places. DO NOT round your mean.
C. Box and Whisker Plots:
1.They are created by using the 5 - number summary, the lowest number, highest number, median, and the lower and upper quartile.
2. The lower quartile is the median of the lower 50% of the data values when ranked from lowest to highest. The upper quartile is the median of the upper 50% of the data values.
3. IQR: Interquartile range is the difference between the upper and lower quartiles. It is the range of the middle 50% of the data.
4. Outliers: Any data values that lie more than 1.5 IQR units below the lower quartile or 1.5 IQR units above the upper quartile.
a. Click on this link to watch a video demonstrating how to construct a box and whisker plot.
b. Practice creating a box plot. One of those problems could be on your exam.
https://www.khanacademy.org/math/probability/data-distributions-a1/box--whisker-plots-a1/e/box-plots
c. Reading box plots.
d. Practice reading box plots. One of those problems could be on your exam.
Finding outliers: Given the following data, determine if there are any outliers.
1, 2, 4, 5, 8, 10, 12, 15
a. Find the median. The median is between 5 and 8. (5 + 8)/2 = 6.5. Notice there are 4 data values below 6.5 and 4 data values above 6.5.
b. Now find the median of the lower 50% of the data. This would be between 2 and 4 or 3. This would be the first quartile.
c. Now find the median of the upper 50% of the data. This would be between 10 and 12 or 11. This is the third quartile.
d. Now find the IQR. This is the difference between the third and first quartile.
11 -3 = 8
e. 3 – (1.5 times 8) = -9. We have no data values below -9
11 + (1.5 times 8) = 23
We have no data values above 23. There for we have no outliers.
Click on this link to practice finding outliers.
D. Percentiles: Data that is divided into 100 equal parts. For example the 23rd percentile would separate the bottom 23% of the data from the top 77% of the data.
Click on this link to see how percentiles are determined.
Practice calculating percentiles
Check in question 5.
Given the following data create a box and whisker plot. (8 points)
30 38, 39, 43, 45, 49, 50, 65
Check in question 6.
Are there any outliers? Please show all your work using the 1.5 rule. (5 points)
Check in question 7.
Determine the percentile the data value 43 would be in. (5 points)
E. Z-score: Indicates how many standard deviations the data value is away from the mean. Data values above the mean have positive z-scores and data values below the mean have negative z-scores. To calculate a z-score: (your data value - mean)/standard deviation.
III. Distributions:
A. Skewness: When the data is stretched out in one direction.
B. Normal distributions: Known as a bell shaped distribution.
If we have a normal distribution we can use the Empirical rule.
IV. Empirical Rule
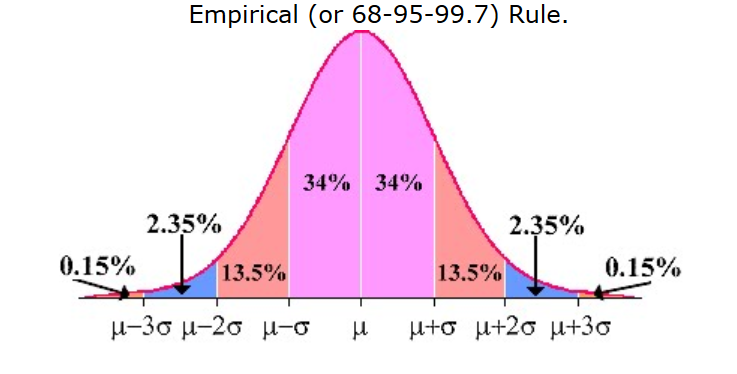
The Empirical Rule states approximately 68% of the data will be within 1 standard deviation of the mean, 95% of the data will be within two standard deviations and 99.7% will be within three standard deviations.
Example:
1. The mean is 50 and the standard deviation is 4. We would expect approximately 68% of the data will be between (50-1(4) to 50 + 1(4).
We would expect approximately 95% of the data to be between 50 – 2(4) to 50 + 2(4) and we would expect 99.7% of the data to be between 50 – 3(4) to 50 + 3(4).
Click on this link to watch a video on the empirical rule.
https://www.youtube.com/watch?v=5HImTBJlWZc&feature=youtu.be
Practice using the Empirical Rule
Check in question 8. Assume for both questions the data is normally distributed.
If the mean for an exam was 87 with a standard deviation of 2.5, determine the z- score for a student scoring a 93.5 on the exam. (5 points)
Check in question 9.
What percentage of student would score between 84.5 and 92? (2 points)

