0.1: Review - Real Numbers: Notation and Operations

Last updated
Save as PDF

Page ID: 38205

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Real Numbers

Algebra is often described as the generalization of arithmetic. The systematic use of variables, letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations.

A set is a collection of objects, typically grouped within braces $\{ \}$, where each object is called an element. When studying mathematics, we focus on special sets of numbers.

\[ \begin{align*} \mathbb { N } &= \underbrace{\{ 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Natural\: Numbers}}
& W &= \underbrace{ \{ 0 , 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Whole\: Numbers}}
&\mathbb{Z} &= \underbrace{ \{\dots ,-3,-2,-1,0,1,2,3,\dots\}}_{\color{Cerulean}{Integers}} \end{align*}\]

The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subset, denoted $\subseteq$, is a set consisting of elements that belong to a given set. Notice that the sets of natural and whole numbers are both subsets of the set of integers and we can write $\mathbb { N } \subseteq \mathbb{Z}$ and $W \subseteq \mathbb{Z}$.

A set with no elements is called the empty set and has its own special notation:

$\{\:\:\:\}=\varnothing\: \qquad \color{Cerulean}{Empty\: Set}$

Rational numbers, denoted $\mathbb{Q}$, are defined as any number of the form $\frac { a } { b }$ where a and b are integers and b is nonzero. We can describe this set using set notation:

$\mathbb { Q } = \left\{ \frac { a } { b } | a , b \in \mathbb { Z } , b \neq 0 \right\} \qquad \color{Cerulean}{Rational\: Numbers}$

The vertical line | inside the braces reads, “such that” and the symbol $\in$ indicates set membership and reads, “is an element of.” The notation above in its entirety reads, “the set of all numbers $\frac{a}{b}$ such that a and b are elements of the set of integers and b is not equal to zero.” Decimals that terminate or repeat are rational. For example, $0.05=\frac{5}{100}$ and $0.\overline{6}=0.6666…=\frac{2}{3} $.

The set of integers is a subset of the set of rational numbers, $\mathbb{Z}\subseteq\mathbb{Q}$, because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example, $7=\frac{7}{1}$.

Irrational numbers are defined as any numbers that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example, $π=3.14159…$ and $\sqrt{2}=1.41421…$.

Finally, the set of real numbers, denoted $\mathbb{R}$, is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,

Notation Used to Define Subsets of Real Numbers

Sets of numbers can be described in several ways, including Interval Notation, Set-Builder Notation and Inequality Notation.

Interval Notation

In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded.

The smallest number in the interval, an endpoint, is written first.
The largest number in the interval, another endpoint, is written second, and is written after a comma.
Parentheses, $($ or $)$, are used to signify that an endpoint is not included in the interval.
Brackets, $[$ or $]$, are used to indicate that an endpoint is included in the interval.

Set Notation

Another way a set of numbers can be described is in set-builder notation. The braces $\{\}$ are read as “the set of,” and the vertical bar $|$ is read as “such that,” so we would read $ \{x|10≤x<30\}$ as “the set of x-values such that 10 is less than or equal to x, and x is less than 30.” For a given value of $x$ the statement is either true or false.

Figure $\PageIndex{2}$ compares inequality notation, set-builder notation, and interval notation.

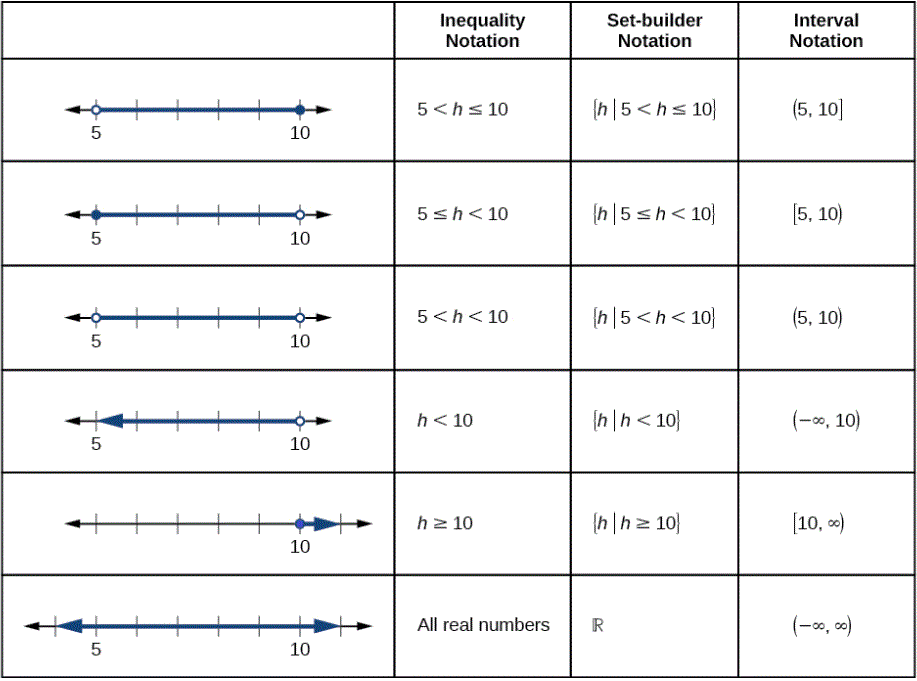
$p.1.1 table1.gif$
Figure $\PageIndex{2}$: Summary of notations for inequalities, sets, and intervals.

$how-to.png$ How to: Given a line graph, describe the set of values using interval notation.

Identify the intervals to be included in the set by determining where the heavy line overlays the real line.
At the left end of each interval, use [ with each end value included in the set (solid dot) or ( for each excluded end value (open dot).
At the right end of each interval, use ] with each end value included in the set (filled dot) or ) for each excluded end value (open dot).
Use the union symbol $\cup$ to combine all intervals into one set.
NOTE: The word "or" (rather than $\cup$) is used to combine sets described by inequalities or Set-builder notation.

Compound Inequalities

For sets with a finite number of elements, like for example the sets $\{2,3,5\}$ and $\{5,6\}$, the union of these sets is the set $\{2,3,5,6\}$. The elements do not have to be listed in ascending order of numerical value, but if the original two sets have some elements in common, those elements should be listed only once in the union set. The intersection of these two set lists only those elements common to both sets, $\{5\}$

Union of intervals

There are several different ways to illustrate the union of two intervals, which combines all the elements of both sets.

For inequality notation or set-builder notation, the word “or” is used. (The logical “or” operation requires that either one or both conditions are true.)
For interval notation, the union symbol $ \cup $ is used to combine all the elements of both sets.

To find the union of two intervals, use the portion of the number line representing the total collection of numbers in the two number line graphs. For example,

Figure $\PageIndex{3}$ Number Line Graph of $x<3$ or $x\geq 6$

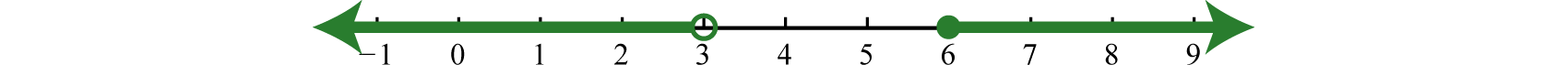
$\color{Cerulean}{Interval notation:}$ $(−∞,3)\cup[6,∞)$

$\color{Cerulean}{Set notation:}$ $\{x| x<3 \text{ or } x\geq 6\}$

Example $\PageIndex{1}$: Describing Sets on the Real-Number Line

Describe the intervals of values shown on the line graph below using inequality notation, set-builder notation, and interval notation.

[Line graph of $1<=x<=3$ and $5$] — Figure $\PageIndex{4}$: Line graph of $ 1≤x≤3 \text{ or } x>5 $.

Solution

To describe the values, $x$, included in the intervals shown, we would say, “$x$ is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”

$ \begin{array} {cl}
1≤x≤3 \text{ or }x>5 &\text{Inequality}\\
\{x|1≤x≤3 \text{ or } x>5\} \qquad & \text{Set-Builder Notation} \\
[1,3]\cup(5,\infty) & \text{Interval Notation} \\
\end{array}$

Remember that when writing or reading interval notation, using a square bracket means the boundary is included in the set. Using a parenthesis means the boundary is not included in the set.

$try-it.png$ Try It $\PageIndex{1}$

Given Figure $\PageIndex{5}$, specify the graphed set in

words
set-builder notation
interval notation

[Line graph of -2<=x, -1<=x<3.] — Figure $\PageIndex{5}$: Line graph

Answers: a. Values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3;
b. $\{x|x≤−2 \text{ or } −1≤x<3\}$
c. $\left(−∞,−2\right]\cup\left[−1,3\right)$

Intersection of intervals

There are several different ways to illustrate the intersection of two intervals.

For inequality notation or set-builder notation, the word “and” is used to signify the intersection of two intervals. (The logical “and” operation requires that both conditions must be true.) The intersection can be more succinctly written as a compound inequality. For example, $−1\leq x$ and $x<3$ can be written more concisely as $−1\leq x<3$ which reads “negative one is less than or equal to x and x is less than three.”
When interval notation is used, the set composed of only the elements common to both sets is denoted by the intersection symbol, $\cap$.

To find the intersection of two intervals, take the portion of the number line that the two number line graphs have in common.

Example $\PageIndex{2}$:

Graph and give the interval notation and set notation equivalent to $x<3$ and $x\geq −1$.

Solution

Determine the intersection, or overlap, of the two solution sets to $x<3$ and $x\geq −1$. The solutions to each inequality are sketched above the number line as a means to determine the intersection, which is graphed on the number line below.

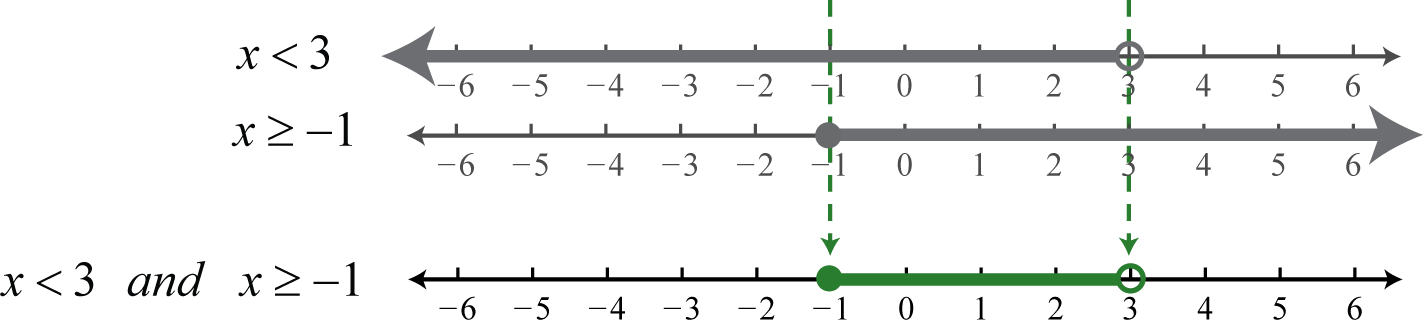
Here, $3$ is not a solution because it solves only one of the inequalities. Alternatively, we may interpret $−1\leq x<3$ as all possible values for x between, or bounded by, $−1$ and $3$ where $−1$ is included in the solution set.

Answer:

Interval notation: $[\,−1, 3)$; set notation: $\{x|−1\leq x<3\}$

Real Number Operations

Order of Operations

When we multiply a number by itself, we square it or raise it to a power of $2$. For example, $4^2 =4\times4=16$. We can raise any number to any power. In general, the exponential notation $a^n$ means that the number or variable $a$ is used as a factor $n$ times.

\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]

In this notation, $a^n$ is read as the $n^{th}$ power of $a$, where $a$ is called the base and $n$ is called the exponent. A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, $24+6 \times \dfrac{2}{3} − 4^2$ is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber\]

There are no grouping symbols, so move on to exponents. The number $4$ is raised to a power of $2$, so simplify $4^2$ as $16$.

\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber \]

\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]

Next, perform multiplication or division, left to right.

\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]

\[24+4-16 \nonumber\]

Lastly, perform addition or subtraction, left to right.

\[24+4−16 \nonumber\]

\[28−16 \nonumber\]

\[12 \nonumber\]

Therefore,

\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

ORDER OF OPERATIONS

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS:

P(arentheses)
E(xponents)
M(ultiplication) and D(ivision)
A(ddition) and S(ubtraction)

$how-to.png$ How to: Given a mathematical expression, simplify it using the order of operations.

Simplify any expressions within grouping symbols. Grouping symbols include parentheses ( ), brackets [ ], braces { }, fraction bars, radicals, and absolute value bars
Simplify any expressions containing exponents or radicals.
Perform any multiplication and division in order, from left to right.
Perform any addition and subtraction in order, from left to right.

Example $\PageIndex{3}$: Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

$(3+2)^2+4 \times(6+2)$
$\dfrac{5^2-4}{7}- \sqrt{11-2}$
$6−|5−8|+3\times(4−1)$ &&
$\dfrac{14-3 \times2}{2 \times5-3^2}$
$7\times(5\times3)−2\times[(6−3)−4^2]+1$

Solution

\[\begin{align*} (3\times2)^2-4\times(6+2)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=4 && \qquad \text{Simplify subtraction}\\ \end{align*}\]
\[\begin{align*} \dfrac{5^2-4}{7}- \sqrt{11-2}&= \dfrac{5^2-4}{7}-\sqrt{9} && \qquad \text{Simplify grouping symbols }\\
&=\dfrac{5^2-4}{7}-3 && \qquad \cdot \text{ radical: Subtract}\\
&=\dfrac{25-4}{7}-3 && \qquad \cdot \text{ numerator: Simplify exponent }\\
&=\dfrac{21}{7}-3 && \qquad \cdot \text{ numerator: Subtract}\\
&=3-3 && \qquad \text{Simplify division}\\
&=0 && \qquad \text{Simplify subtraction} \end{align*}\]

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

\[\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+3\times3 && \qquad \text{Simplify inside grouping symbols}\\ &=6-3+3\times3 && \qquad \text{Simplify absolute value}\\ &=6-3+9 && \qquad \text{Simplify multiplication}\\ &=3+9 && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \end{align*}\]
\[\begin{align*} \dfrac{14-3 \times2}{2 \times5-3^2}&=\dfrac{14-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{1} && \qquad \text{Simplify differences}\\ &=8 && \qquad \text{Simplify quotient}\\ \end{align*}\]

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

\[\begin{align*} 7\times(5\times3)-2\times[(6-3)-4^2]+1&=7\times(15)-2\times[(3)-4^2]+1 && \qquad \text{Simplify inside parentheses}\\ &=7\times(15)-2\times(3-16)+1 && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+1 && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \end{align*}\]

$try-it.png$ Try It $\PageIndex{3}$

Use the order of operations to evaluate each of the following expressions.

$\sqrt{5^2-4^2}+7\times(5-4)^2$
$1+\dfrac{7\times5-8\times4}{9-6}$
$|1.8-4.3|+0.4\times\sqrt{15+10}$
$\dfrac{1}{2}\times[5\times3^2-7^2]+\dfrac{1}{3}\times9^2$
$[(3-8^2)-4]-(3-8)$

Answer: a. $10$ $ \qquad $ b. $2$ $ \qquad $ c. $4.5$ $ \qquad $ d. $25$ $ \qquad $ e. $-60$

Real Number Properties

PROPERTIES OF REAL NUMBERS

The following properties hold for real numbers $a$, $b$, and $c$.

	Addition	Multiplication
Commutative Property	$a+b=b+a$	$a\times b=b\times a$
Associative Property	$a+(b+c)=(a+b)+c$	$a(bc)=(ab)c$
Distributive Property	$a\times (b+c)=a\times b+a\times c$
Identity Property	There exists a unique real number called the additive identity, 0, such that, for any real number $a$ $a+0=a$	There exists a unique real number called the multiplicative identity, 1, such that, for any real number $a$ $a\times 1=a$
Inverse Property	Every real number $a$ has an additive inverse, or opposite, denoted $–a$, such that $a+(−a)=0$	Every nonzero real number $a$ has a multiplicative inverse, or reciprocal, denoted $\frac{1}{a}$ , such that $a\times \left(\dfrac{1}{a}\right)=1$

Constants and Variables

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as $x +5$, $\dfrac{4}{3}\pi r^3$, or $\sqrt{2m^3 n^2}$. In the expression $x +5$, $5$ is called a constant because it does not vary and $x$ is called a variable because it does. (In naming the variable, ignore any exponents or radicals included with the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

Example $\PageIndex{4}$: Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

a. $x + 5$

b. $\dfrac{4}{3}\pi r^3$

c. $\sqrt{2m^3 n^2}$

Solution

	a. $x + 5$	b. $\dfrac{4}{3}\pi r^3$	c. $\sqrt{2m^3 n^2}$
Constants	$5$	$\dfrac{4}{3}$, $\pi$	$2$
Variables	$x$	$r$	$m$, $n$

$try-it.png$ Try It $\PageIndex{4}$

List the constants and variables for each algebraic expression.

$2\pi r(r+h)$
$2(L + W)$
$4y^3+y$

Answer

	a. $2\pi r(r+h)$	b. $2(L + W)$	c. $4y^3+y$
Constants	$2$,$\pi$	$2$	$4$
Variables	$r$,$h$	$L$, $W$	$y$

Evaluating Algebraic Expressions

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \quad \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. Parentheses should be used to avoid ambiguity. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Example $\PageIndex{5}$: Evaluating an Algebraic Expression at Different Values

Evaluate the expression $2x−7$ for each value for $x$.

$x=0$
$x=1$
$x=12$
$x=−4$

Solution

Substitute $0$ for $x$. $ \quad 2x-7 = 2(0)-7 = 0-7= -7 $
Notice if parentheses were not used, $2(0)$ would have been $20$, which is incorrect!!!
Substitute $1$ for $x$. $ \quad2x-7 = 2(1)-7= 2-7= -5 $
Substitute $\dfrac{1}{2}$ for $x$. $ \quad 2x-7 = 2\left (\dfrac{1}{2} \right )-7 = 1-7= -6 $
Substitute $-4$ for $x$. $ \quad 2x-7 = 2(-4)-7= -8-7= -15 $
Notice if parentheses were not used, $2(-4)$ which is $-6$, would have been \2 - 4\) or $-2$, which is incorrect!!!

ALWAYS use parentheses in situations where not using them would create an incorrect expression!

$try-it.png$ Try It $\PageIndex{5}$

Evaluate the expression $11−3y$ for each value for $y$.

$y=2$
$y=0$
$y=\dfrac{2}{3}$
$y=−5$

Answer: a. $5$ $ \qquad$ b. $11$$ \qquad$ c. $9$$ \qquad$ d. $26$

Example $\PageIndex{6}$: Evaluating Algebraic Expressions

Evaluate each expression for the given values.

$x+5$ for $x=-5$
$\dfrac{t}{2t-1}$ for $t=10$
$\dfrac{4}{3}\pi r^3$ for $r=5$
$a+ab+b$ for $a=11$ , $b=-8$
$\sqrt{2m^3 n^2}$ for $m=2$ , $n=3$

Solution

$-5$ for $x$. \[\begin{align*} x+5 &= (-5)+5 = 0\\ \end{align*}\]
Substitute $10$ for $t$. \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}= \dfrac{10}{19}\\ \end{align*}\]
Substitute $5$ for $r$. \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)= \dfrac{500}{3}\pi\\ \end{align*}\]
Substitute $11$ for $a$ and $-8$ for $b$. \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 = -85\\ \end{align*}\]
Substitute $2$ for $m$ and $3$ for $n$. \[\begin{align*} \sqrt{2m^3 n^2} &= \sqrt{2(2)^3 (3)^2} \\ &= \sqrt{2(8)(9)} \\ &= \sqrt{144} = 12 \end{align*}\]

$try-it.png$ Try It $\PageIndex{6}$

Evaluate each expression for the given values.

$\dfrac{y+3}{y-3}$ for $y=5$
$7-2t$ for $t=-2$
$\dfrac{1}{3}\pi r^2$ for $r=11$
$(p^2 q)^3$ for $p=-2$, $q=3$
$4(m-n)-5(n-m)$ for $m=\dfrac{2}{3}$ $n=\dfrac{1}{3}$

Answer: a. $4$ $ \qquad$ b. $11$ $ \qquad$ c. $\dfrac{121}{3}\pi$ $ \qquad$ d. $1728$ $ \qquad$ e. $3$

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Example $\PageIndex{7}$: Simplifying Algebraic Expressions

Simplify each algebraic expression.

$3x-2y+x-3y-7$
$2r-5(3-r)+4$
$\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)$
$2mn-5m+3mn+n$

Solution

\[\begin{align*} 3x-2y+x-3y-7&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
\[\begin{align*} 2r-5(3-r)+4&=2r-15+5r+4 && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5r-15+4 && \qquad \qquad \qquad \text{Commutative property of addition}\\ &=7r-11 && \qquad \qquad \qquad \text{Simplify}\\ \end{align*}\]
\[\begin{align*} \left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{4}s-2s && \qquad \text{Commutative property of addition}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \end{align*}\]
\[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of addition}\\ &=5mn-5m+n && \qquad \text{Simplify} \end{align*}\]

$try-it.png$ Try It $\PageIndex{7}$

Simplify each algebraic expression.

$\dfrac{2}{3}y−2\left(\dfrac{4}{3}y+z\right)$
$\dfrac{5}{t}−2−\dfrac{3}{t}+1$
$4p(q−1)+q(1−p)$
$9r−(s+2r)+(6−s)$

Answer: a. $−2y−2z$ or $−2(y+z)$ $ \qquad$ b. $\dfrac{2}{t}−1$ $ \qquad$c. $3pq−4p+q$ $ \qquad$d.$7r−2s+6$

Example $\PageIndex{8}$: Simplifying a Formula

A rectangle with length $L$ and width $W$ has a perimeter $P$ given by $P =L+W+L+W$ . Simplify this expression.

Solution

\[\begin{align*} P &=L+W+L+W\\ P &=L+L+W+W && \qquad \text{Commutative property of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive property} \end{align*}\]

$try-it.png$ Try It $\PageIndex{8}$

If the amount $P$ is deposited into an account paying simple interest $r$ for time $t$ , the total value of the deposit $A$ is given by $A =P+Prt$ . Simplify the expression. (This formula will be explored in more detail later in the course.)

Answer: $A=P(1+rt)$

Glossary

algebraic expression: constants and variables combined using addition, subtraction, multiplication, and division

associative property of addition: the sum of three numbers may be grouped differently without affecting the result; in symbols, a+(b+c) = (a+b)+c

associative property of multiplication: the product of three numbers may be grouped differently without affecting the result; in symbols, a(bc) = (ab)c

base: in exponential notation, the expression that is being multiplied

commutative property of addition: two numbers may be added in either order without affecting the result; in symbols, a + b = b + a

commutative property of multiplication: two numbers may be multiplied in any order without affecting the result; in symbols, ab = ba

constant: a quantity that does not change value

distributive property: the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols, a(b+c) = ab + ac

equation: a mathematical statement indicating that two expressions are equal

exponent: in exponential notation, the raised number or variable that indicates how many times the base is being multiplied

exponential notation: a shorthand method of writing products of the same factor

formula: an equation expressing a relationship between constant and variable quantities

identity property of addition: there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols, a + 0 = a

identity property of multiplication: there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols, $ a \cdot 1 = a$

integers: the set consisting of the natural numbers, their opposites, and 0: { ... -3, -2, -1, 0, 1, 2, 3, ... }

inverse property of addition: for every real number $a$ there is a unique number, called the additive inverse (or opposite), denoted $-a$; which, when added to the original number, results in the additive identity, 0; in symbols, $ a + (-a) = 0 $

inverse property of multiplication: for every non-zero real number $a$ there is a unique number, called the multiplicative inverse (or reciprocal), denoted $ \frac{1}{a} $ which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols $ a \cdot \frac{1}{a} = 1$.

irrational numbers: the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers

natural numbers: the set of counting numbers: {1, 2, 3, ...}.

order of operations: a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations

rational numbers: the set of all numbers of the form $\frac{m}{n}$ where $m$ and $n$ are integers and $n \ne 0$. Any rational number may be written as a fraction or a terminating or repeating decimal.

real number line: a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.

real numbers: the sets of rational numbers and irrational numbers taken together

variable: a quantity that may change value

whole numbers: the set consisting of 0 plus the natural numbers: {0, 1, 2, 3, ...}.

	a. \(x + 5\)	b. \(\dfrac{4}{3}\pi r^3\)	c. \(\sqrt{2m^3 n^2}\)
Constants	\(5\)	\(\dfrac{4}{3}\), \(\pi\)	\(2\)
Variables	\(x\)	\(r\)	\(m\), \(n\)

	a. \(2\pi r(r+h)\)	b. \(2(L + W)\)	c. \(4y^3+y\)
Constants	\(2\),\(\pi\)	\(2\)	\(4\)
Variables	\(r\),\(h\)	\(L\), \(W\)	\(y\)