0.3: Review - Radicals (Square Roots)
- Page ID
- 38216
Evaluating Square Roots
When the square root of a number is squared, the result is the original number. Since \(4^2=16\), the square root of \(16\) is \(4\).The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.
In general terms, if \(a\) is a positive real number, then the square root of \(a\) is a number that, when multiplied by itself, gives \(a\). The square root could be positive or negative because multiplying two negative numbers gives a positive number. However, the \( \sqrt{ \text{ } } \) symbol denotes just the non-negative result, or so-called principal square root. The square root obtained using a calculator is the principal square root.
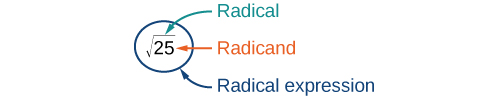
The principal square root is the nonnegative number that when multiplied by itself equals \(a\). The principal square root of \(a\) is written as \(\sqrt{a}\). The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.
Example \(\PageIndex{1}\)
Does \(\sqrt{25} = \pm 5\)?
Solution
No. Although both \(5^2\) and \((−5)^2\) are \(25\), the radical symbol implies only a nonnegative root, the principal square root. The principal square root of \(25\) is \(\sqrt{25}=5\).
Definition: Principal Square Root
The principal square root of \(a\) is the nonnegative number that, when multiplied by itself, equals \(a\). It is written as a radical expression \(\sqrt{a}\), with the symbol called a radical, over the term \(a\), called the radicand. \(\sqrt{a}\).
Example \(\PageIndex{2}\): Evaluating Square Roots
Evaluate each expression.- \(\sqrt{100}\)
- \(\sqrt{\sqrt{16}}\)
- \(\sqrt{25+144}\)
- \(\sqrt{49}\)-\(\sqrt{81}\)
Solution
- \(\sqrt{100} =10\) because \(10^2=100\)
- \(\sqrt{\sqrt{16}}= \sqrt{4} =2\) because \(4^2=16\) and \(2^2=4\)
- \(\sqrt{25+144} = \sqrt{169} =13\) because \(13^2=169\)
- \(\sqrt{49} -\sqrt{81} =7−9 =−2\) because \(7^2=49\) and \(9^2=81\)
Example \(\PageIndex{3}\):
For \(\sqrt{25+144}\), can we find the square roots before adding?
Solution
No. \(\sqrt{25} + \sqrt{144} =5+12=17\). This is not equivalent to \(\sqrt{25+144}=13\). The order of operations requires us to add the terms of the radicand together before finding the square root.
![]() Try It \(\PageIndex{3}\)
Try It \(\PageIndex{3}\)
Evaluate each expression.
| a. \(\sqrt{25}\) | b. \(\sqrt{\sqrt{81}}\) | c. \(\sqrt{25-9}\) | d. \(\sqrt{36} + \sqrt{121}\) |
- Answers
- a. \(5\) \( \qquad \) b. \(3\) \( \qquad \) c.\(4\) \( \qquad \) d. \(17\)
Using the Product Rule to Simplify Square Roots
To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite \(\sqrt{15}\) as \(\sqrt{3}\times\sqrt{5}\). We can also use the product rule to express the product of multiple radical expressions as a single radical expression.
The Product Rule For Simplifying Square Roots
If \(a\) and \(b\) are nonnegative, the square root of the product \(ab\) is equal to the product of the square roots of \(a\) and \(b\)
\[\sqrt{ab}=\sqrt{a}\times\sqrt{b}\]
![]() How to: Simplify the square root of a product.
How to: Simplify the square root of a product.
- Factor any perfect squares from the radicand.
- Write the radical expression as a product of radical expressions.
- Simplify.
Example \(\PageIndex{4}\): Using the Product Rule to Simplify Square Roots
Simplify the radical expression.
- \(\sqrt{300}\)
- \(\sqrt{162a^5b^4}\)
Solution
a. \( \quad \sqrt{100\times3} \) Factor perfect square from radicand.
\( \sqrt{100}\times\sqrt{3} \) Write radical expression as product of radical expressions.
\( 10\sqrt{3}\) Simplify
b. \( \quad \sqrt{81a^4b^4\times2a}\) Factor perfect square from radicand
\(\sqrt{81a^4b^4}\times\sqrt{2a}\) Write radical expression as product of radical expressions
\(9a^2b^2\sqrt{2a}\) Simplify
![]() Try It \(\PageIndex{4}\)
Try It \(\PageIndex{4}\)
Simplify \(\sqrt{50x^2y^3z}\)
- Answer
-
\(5|x||y|\sqrt{2yz}\)
Notice the absolute value signs around \(x\) and \(y\)? That’s because their value must be positive!
![]() How to: Simplify the product of multiple radical expressions
How to: Simplify the product of multiple radical expressions
- Express the product of multiple radical expressions as a single radical expression.
- Simplify.
Example \(\PageIndex{5}\): Using the Product Rule to Simplify the Product of Multiple Square Roots
Multiply. Simplify the radical expression.
a. \(\sqrt{12}\times\sqrt{3}\)
b. \(\sqrt { 6 x ^ { 3 } y ^ { 3 } } \times \sqrt{2 x^3} \).
Solution
a. \( \quad \text{Express the product as a single radical expression: } \sqrt{12\times3} = \sqrt{36} = 6 \)
b. \( \quad \)Begin by writing as a single radical expression: \(\sqrt { 12 x ^ { 6 } y ^ { 3 } }\).
Determine the square factors of \(12, x^{ 6}\) , and \(y^{ 3}\).
\(\left. \begin{array} { l } { 12 = \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 } \\ { x ^ { 6 } = \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 } }} \\ { y ^ { 3 } = \color{Cerulean}{y ^ { 2} }\color{black}{ \cdot} y } \end{array} \right\} \quad\color{Cerulean}{Square\:factors}\)
Make these substitutions, and then apply the product rule for radicals and simplify.
\(\begin{aligned} \sqrt { 12 x ^ { 6 } y ^ { 3 } } & = \sqrt { \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 \cdot \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 }}\color{black}{ \cdot}\color{Cerulean}{ y ^ { 2} }\color{black}{ \cdot} y } \quad\quad\quad\quad\:\color{Cerulean} { Apply\:the\: product \:rule\: for\: radicals. } \\ & = \sqrt { 2 ^ { 2 } } \cdot \sqrt { \left( x ^ { 3 } \right) ^ { 2 } } \cdot \sqrt { y ^ { 2 } } \cdot \sqrt { 3 y } \quad\color{Cerulean} { Simplify. } \\ & = 2 \cdot x ^ { 3 } \cdot | y | \cdot \sqrt { 3 y } \\ & = 2 x ^ { 3 } | y | \sqrt { 3 y } \end{aligned}\)
Notice the absolute value bars around \( y \). That is because the result of taking a square root is never negative.
![]() Try It \(\PageIndex{5}\)
Try It \(\PageIndex{5}\)
Simplify \(\sqrt{50x}\times\sqrt{2x}\) assuming \(x>0\).
- Answer
-
\(10|x|\)
Using the Quotient Rule to Simplify Square Roots
Just as we can rewrite the square root of a product as a product of square roots, so too can we rewrite the square root of a quotient as a quotient of square roots, using the quotient rule for simplifying square roots.
THE QUOTIENT RULE FOR SIMPLIFYING SQUARE ROOTS
The square root of the quotient \(\dfrac{a}{b}\) is equal to the quotient of the square roots of \(a\) and \(b\) , where \(a \ge 0\) and \(b > 0\) .
\[\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}\]
![]() How to: Simplify the radical of a quotient
How to: Simplify the radical of a quotient
- Simplify the quotient radicand.
- Write the simplified quotient radical expression as the quotient of two radical expressions.
- Simplify the numerator and denominator.
Example \(\PageIndex{6}\): Using the Quotient Rule to Simplify Square Roots
Simplify the radical expression.
| a. \(\sqrt{\dfrac{5}{36}}\) | b. \(\sqrt { \dfrac { 18 a ^ { 5 } } { b ^ { 8 } } }\) |
a. Write as a quotient of two radical expressions and then simplify the denominator: \(\dfrac{\sqrt{5}}{\sqrt{36} = \dfrac{\sqrt{5}}{6}\)
b. Begin by determining the square factors of \(18\), \(a^{5}\), and \(b^{8}\).
\(\left. \begin{array} { l } { 18 = 2 \cdot \color{Cerulean}{3 ^ { 2} } } \\ { a ^ { 5 } = a ^ { 2 } \cdot a ^ { 2 } \cdot a = \color{Cerulean}{\left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } \\ { b ^ { 8 } = b ^ { 4 } \cdot b ^ { 4 } \quad\:\:= \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 }} } \end{array}\quad \right\}\quad\color{Cerulean}{Square\:factors}\)
\( \quad \) Make these substitutions, apply the product and quotient rules for radicals, and then simplify.
\(\begin{aligned} \sqrt { \frac { 18 a ^ { 5 } } { b ^ { 8 } } } & = \sqrt { \frac { 2 \cdot \color{Cerulean}{3 ^ { 2} }\color{black}{ \cdot}\color{Cerulean}{ \left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } { \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 } } }}\quad\quad\color{Cerulean}{Apply\:the\:product\:and\:quotient\:rule\:for\:radicals.} \\ & = \frac { \sqrt { 3 ^ { 2 } } \cdot \sqrt { \left( a ^ { 2 } \right) ^ { 2 } } \cdot \sqrt { 2 a } } { \sqrt { \left( b ^ { 4 } \right) ^ { 2 } } }\quad \color{Cerulean}{Simplify.} \\ & = \frac { 3 a ^ { 2 } \sqrt { 2 a } } { b ^ { 4 } } \end{aligned}\)
![]() Try It \(\PageIndex{6}\)
Try It \(\PageIndex{6}\)
Simplify \(\sqrt{\dfrac{2x^2}{9y^4}}\)
- Answer
-
\(\dfrac{|x|\sqrt{2}}{3y^2} \quad \) We do not need the absolute value signs for \(y^2\) because that term will always be nonnegative.
![]() How to: Simplify the quotient of multiple radical expressions
How to: Simplify the quotient of multiple radical expressions
- Express the quotient of multiple radical expressions as a quotient of a single radical expression.
- Simplify the radical.
Example \(\PageIndex{7}\): Use the Quotient Rule to Simplify the Quotient of Two Square Roots
Divide. Simplify the radical expression.
| a. \(\dfrac{\sqrt{234x^{11}y}}{\sqrt{26x^7y}}\) | b. \( \dfrac { \sqrt {50 x^6 y^4} } { \sqrt {8 x^3 y} } \) |
Solution
a. First combine numerator and denominator into one radical expression
\(\begin{align*}
\dfrac { \sqrt { 50 x ^ { 6 } y ^ { 4} } } { \sqrt { 8 x ^ { 3 } y } }&=\sqrt{\dfrac{234x^{11}y}{26x^7y}} & & \text{Write under one radical}\\[5pt]
&=\sqrt{9x^4} & & \text{Simplify radicand}\\[5pt]
&=3x^2 & & \text{Simplify square root}
\end{align*}\)
b. Write as a single square root and cancel common factors before simplifying.
\(\begin{aligned} \frac { \sqrt { 50 x ^ { 6 } y ^ { 4 } } } { \sqrt { 8 x ^ { 3 } y } } & = \sqrt { \frac { 50 x ^ { 6 } y ^ { 4 } } { 8 x ^ { 3 } y } } \quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals\:and\:cancel.}\\ & = \sqrt { \frac { 25 x ^ { 3 } y ^ { 3 } } { 4 } } \quad\color{Cerulean}{Simplify.} \\ & = \frac { \sqrt { 25 x ^ { 3 } y ^ { 3 } } } { \sqrt { 4 } } \\ & = \frac { 5 |x y| \sqrt { x y } } { 2 } \end{aligned}\)
![]() Try It \(\PageIndex{7}\)
Try It \(\PageIndex{7}\)
Simplify \(\dfrac{\sqrt{9a^5b^{14}}}{\sqrt{3a^4b^5}}\)
- Answer
-
\(b^4\sqrt{3ab}\)
\( \boxed{ \text{From this point on the assumption will be made that all variables represent non-negative real numbers.} \\ \text{Therefore using absolute values when simplifying will not be necessary.} } \)
Adding and Subtracting Square Roots
We can add or subtract radical expressions only when they have the same radicand and when they have the same radical type such as square roots. For example, the sum of \(\sqrt{2}\) and \(3\sqrt{2}\) is \(4\sqrt{2}\). However, it is often possible to simplify radical expressions, and that may change the radicand. The radical expression \(\sqrt{18}\) can be written with a \(2\) in the radicand, as \(3\sqrt{2}\), so \(\sqrt{2}+\sqrt{18}=\sqrt{2}+3\sqrt{2}=4\sqrt{2}\)
![]() How to: Simplify a radical expression requiring addition or subtraction of square roots
How to: Simplify a radical expression requiring addition or subtraction of square roots
- Simplify each radical expression.
- Add or subtract expressions with equal radicands.
Often, we will have to simplify before we can identify the like radicals within the terms. If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.
Example \(\PageIndex{8}\): Add or Subtract Square Roots
Perform the indicated operation and simplify.
- \(4 \sqrt { 10 } - 5 \sqrt { 10 } \)
- \(5\sqrt{12}+2\sqrt{3}\).
- \(20\sqrt{72a^3b^4c}-14\sqrt{8a^3b^4c}\)
Solution
a. \(\begin{aligned} \text{ }& \text{ } \\ & \text{ } && = ( 4 - 5 ) \sqrt { 10 } \\ & & &= - 1 \sqrt { 10 } \\ & & &= - \sqrt { 10 } \end{aligned}\)
b. \( \quad \)We can rewrite \(5\sqrt{12}\) as \(5\sqrt{4\times3}\). According the product rule, this becomes \(5\sqrt{4}\sqrt{3}\). The square root of \(\sqrt{4}\) is \(2\) , so the expression becomes \(5\times2\sqrt{3}\), which is \(10\sqrt{3}\). Now we can the terms have the same radicand so we can add.
\[10\sqrt{3}+2\sqrt{3}=12\sqrt{3} \nonumber\]
c. \( \quad \)Rewrite each term so they have equal radicands.
\[\begin{align*} 20\sqrt{72a^3b^4c} &= 20\sqrt{9}\sqrt{4}\sqrt{2}\sqrt{a}\sqrt{a^2}\sqrt{(b^2)^2}\sqrt{c}\\ &= 20(3)(2)|a|b^2\sqrt{2ac}\\ &= 120|a|b^2\sqrt{2ac} \end{align*}\]
\[\begin{align*} 14\sqrt{8a^3b^4c} &= 14\sqrt{2}\sqrt{4}\sqrt{a}\sqrt{a^2}\sqrt{(b^2)^2}\sqrt{c}\\ &= 14(2)|a|b^2\sqrt{2ac}\\ &= 28|a|b^2\sqrt{2ac} \end{align*}\]
Now the terms have the same radicand so we can subtract.
\[120|a|b^2\sqrt{2ac}-28|a|b^2\sqrt{2ac}=92|a|b^2\sqrt{2ac}\]
![]() Try It \(\PageIndex{8}\)
Try It \(\PageIndex{8}\)
- Add \(\sqrt{5}+6\sqrt{20}\)
- Subtract \(3\sqrt{80x}-4\sqrt{45x}\)
- Answers
-
a. \(13\sqrt{5}\) \( \qquad \) b. \(0\)
Example \(\PageIndex{9}\): Adding and Subtracting Square Roots
Simplify.
- \( 10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 } \)
- \( \sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 } \)
- \(2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b }\).
Solution
a.
\(\begin{aligned} & \text{ } && = \color{Cerulean}{10 \sqrt { 5 } - 9 \sqrt { 5 }}\color{black}{ +}\color{OliveGreen}{ 6 \sqrt { 2 } - 7 \sqrt { 2 }} \\ &&& = \sqrt { 5 } - \sqrt { 2 } \end{aligned}\)
We cannot simplify any further because \(\sqrt{5}\) and \(\sqrt{2}\) are not like radicals; the radicands are not the same.
\(\color{YellowOrange}{\text{Caution:}}\) It is important to point out that \(\sqrt { 5 } - \sqrt { 2 } \neq \sqrt { 5 - 2 }\). We can verify this by calculating the value of each side with a calculator.
\( \sqrt { 5 } - \sqrt { 2 } \approx 0.82 \qquad \text{ is not the same as } \qquad \sqrt { 5 - 2 } = \sqrt { 3 } \approx 1.73 \)
b.
\(\begin{aligned} & \text{ } && = \sqrt { 16 } \cdot 2 - \sqrt { 9 \cdot 2 } + \sqrt { 25 \cdot 2 } \\ &&& = 4 \sqrt { 2 } - 3 \sqrt { 2 } + 5 \sqrt { 2 } \\ &&& = 6 \sqrt { 2 } \end{aligned}\)
At first glance, the radicals do not appear to be similar. However, after simplifying completely, we see that we can combine them.
c. \( \;\) Step 1: Simplify the radical expression.
\( \quad \) Step 2: Combine all like radicals. Remember to add only the coefficients; the variable parts remain the same.
\(\begin{array} { l } { 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b } } \\ { = 2 a \sqrt { 25 \cdot 5 \cdot a ^ { 2 } \cdot b } - a ^ { 2 } \sqrt { 16 \cdot 5 \cdot b } + 4 \sqrt { 4 \cdot 5 \cdot \left( a ^ { 2 } \right) ^ { 2 } b } }\quad\color{Cerulean}{Factor.} \\ { = 2 a \cdot 5 \cdot a \sqrt { 5 b } - a ^ { 2 } \cdot 4 \sqrt { 5 b } + 4 \cdot 2 \cdot a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\:\color{Cerulean}{ Simplify.} \\ { = 10 a ^ { 2 } \sqrt { 5 b } - 4 a ^ { 2 } \sqrt { 5 b } + 8 a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\quad\quad\quad\quad \color{Cerulean}{Combine\:like\:terms.} \\ { = 14 a ^ { 2 } \sqrt { 5 b } } \end{array}\)
![]() Try It \(\PageIndex{9}\)
Try It \(\PageIndex{9}\)
Simplify: \(\sqrt { 20 } + \sqrt { 27 } - 3 \sqrt { 5 } - 2 \sqrt { 12 }\).
- Answer
-
\(- \sqrt { 5 } - \sqrt { 3 }\)
Caution: Simplifying Radicals
Take careful note of the differences between products and sums within a radical. Assume both \(x\) and \(y\) are nonnegative.
\(\begin{array} { l } Products \quad \quad\quad\quad Sums\\\hline { \sqrt { x ^ { 2 } y ^ { 2 } } = x y \quad\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y } \end{array}\)
The property says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.
Simplifying Products of Expressions containing Square Roots
Often, there will be coefficients in front of the radicals.
Example \(\PageIndex{10.1x}\):
Multiply: \(3 \sqrt { 6 } \cdot 5 \sqrt { 2 }\)
Solution
Using the product rule for radicals and the fact that multiplication is commutative, we can multiply the coefficients and the radicands as follows.
\(\begin{aligned} 3 \sqrt { 6 } \cdot 5 \sqrt { 2 } & = \color{Cerulean}{3 \cdot 5}\color{black}{ \cdot}\color{OliveGreen}{ \sqrt { 6 } \cdot \sqrt { 2} }\quad\color{Cerulean}{Multiplication\:is\:commutative.} \\ & = 15 \cdot \sqrt { 12 } \quad\quad\quad\:\color{Cerulean}{Multiply\:the\:coefficients\:and\:the\:radicands.} \\ & = 15 \sqrt { 4 \cdot 3 } \quad\quad\quad\:\color{Cerulean}{Simplify.} \\ & = 15 \cdot 2 \cdot \sqrt { 3 } \\ & = 30 \sqrt { 3 } \end{aligned}\)
Typically, the first step involving the application of the commutative property is not shown.
We will often find the need to subtract a radical expression with multiple terms. If this is the case, remember to apply the distributive property before combining like terms.
Example \(\PageIndex{10.2x}\): Use the distributive property with square roots
\(\begin{aligned} & \text{Simplify: } ( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } ) && \text{Solution:} \\ \text{ }& \text{ } \\ & \text{ } && = 5 \sqrt { x } - 4 \sqrt { y } - 4 \sqrt { x } + 7 \sqrt { y } \quad\color{Cerulean}{Distribute.} \\ &&& = 5 \sqrt { x } - 4 \sqrt { x } - 4 \sqrt { y } + 7 \sqrt { y } \\ &&& = \sqrt { x } + 3 \sqrt { y } \end{aligned}\)
Use the distributive property when multiplying rational expressions with more than one term.
Example \(\PageIndex{10.3x}\):
Multiply: \(5 \sqrt { 2 x } ( 3 \sqrt { x } - \sqrt { 2 x } )\).
Solution:
Apply the distributive property and multiply each term by \(5 \sqrt { 2 x }\).
\(\begin{aligned} 5 \sqrt { 2 x } ( 3 \sqrt { x } - \sqrt { 2 x } ) & = \color{Cerulean}{5 \sqrt { 2 x } }\color{black}{\cdot} 3 \sqrt { x } - \color{Cerulean}{5 \sqrt { 2 x }}\color{black}{ \cdot} \sqrt { 2 x } \quad\color{Cerulean}{Distribute.}\\ & = 15 \sqrt { 2 x ^ { 2 } } - 5 \sqrt { 4 x ^ { 2 } } \quad\quad\quad\quad\:\:\:\color{Cerulean}{Simplify.} \\ & = 15 x \sqrt { 2 } - 5 \cdot 2 x \\ & = 15 x \sqrt { 2 } - 10 x \end{aligned}\)
The process for multiplying radical expressions with multiple terms is the same process used when multiplying polynomials. Apply the distributive property, simplify each radical, and then combine like terms.
Example \(\PageIndex{10.4x}\):
Multiply: \(( \sqrt { x } - 5 \sqrt { y } ) ^ { 2 }\).
Solution
\(( \sqrt { x } - 5 \sqrt { y } ) ^ { 2 } = ( \sqrt { x } - 5 \sqrt { y } ) ( \sqrt { x } - 5 \sqrt { y } )\)
Begin by applying the distributive property.

\(\begin{array} { l } { = \color{Cerulean}{\sqrt { x }}\color{black}{ \cdot} \sqrt { x } + \color{Cerulean}{\sqrt { x }}\color{black}{ (} - 5 \sqrt { y } ) + ( \color{OliveGreen}{- 5 \sqrt { y }}\color{black}{ )} \sqrt { x } + ( \color{OliveGreen}{- 5 \sqrt { y }}\color{black}{ )} ( - 5 \sqrt { y } ) } \\ { = \sqrt { x ^ { 2 } } - 5 \sqrt { x y } - 5 \sqrt { x y } + 25 \sqrt { y ^ { 2 } } } \\ { = x - 10 \sqrt { x y } + 25 y } \end{array}\)
The binomials \((a + b)\) and \((a − b)\) are called conjugates. When multiplying conjugate binomials the middle terms are opposites and their sum is zero.
Example \(\PageIndex{10.5x}\):
Multiply: \(( \sqrt { 10 } + \sqrt { 3 } ) ( \sqrt { 10 } - \sqrt { 3 } )\).
Solution
Apply the distributive property, and then combine like terms.
\(\begin{aligned} ( \sqrt { 10 } + \sqrt { 3 } ) ( \sqrt { 10 } - \sqrt { 3 } ) & = \color{Cerulean}{\sqrt { 10} }\color{black}{ \cdot} \sqrt { 10 } + \color{Cerulean}{\sqrt { 10} }\color{black}{ (} - \sqrt { 3 } ) + \color{OliveGreen}{\sqrt{3}}\color{black}{ (}\sqrt{10}) + \color{OliveGreen}{\sqrt{3}}\color{black}{(}-\sqrt{3}) \\ & = \sqrt { 100 } - \sqrt { 30 } + \sqrt { 30 } - \sqrt { 9 } \\ & = 10 - \color{red}{\sqrt { 30 }}\color{black}{ +}\color{red}{ \sqrt { 30} }\color{black}{ -} 3 \\ & = 10 - 3 \\ & = 7 \\ \end{aligned}\)
It is important to note that when multiplying conjugate radical expressions, we obtain a rational expression. This is true in general
\(\begin{aligned} ( \sqrt { x } + \sqrt { y } ) ( \sqrt { x } - \sqrt { y } ) & = \sqrt { x ^ { 2 } } - \sqrt { x y } + \sqrt {x y } - \sqrt { y ^ { 2 } } \\ & = x - y \end{aligned}\)
Alternatively, using the formula for the difference of squares we have,
\(\begin{aligned} ( a + b ) ( a - b ) & = a ^ { 2 } - b ^ { 2 }\quad\quad\quad\color{Cerulean}{Difference\:of\:squares.} \\ ( \sqrt { x } + \sqrt { y } ) ( \sqrt { x } - \sqrt { y } ) & = ( \sqrt { x } ) ^ { 2 } - ( \sqrt { y } ) ^ { 2 } \\ & = x - y \end{aligned}\)
![]() Try It \(\PageIndex{10x}\)
Try It \(\PageIndex{10x}\)
Multiply: \(( 3 - 2 \sqrt { y } ) ( 3 + 2 \sqrt { y } )\). (Assume \(y\) is positive).
- Answer
-
\(9-4y\)
Rationalizing Denominators
When an expression involving square root radicals is written in simplest form, it will not contain a radical in the denominator. We can remove radicals from the denominators of fractions using a process called rationalizing the denominator.
We know that multiplying by \(1\) does not change the value of an expression. We use this property of multiplication to change expressions that contain radicals in the denominator. To remove radicals from the denominators of fractions, multiply by the form of \(1\) that will eliminate the radical.
Monomial Denominators
For a denominator containing a single term, multiply by the radical in the denominator over itself. In other words, if the denominator is \(b\sqrt{c}\), multiply by \(\dfrac{\sqrt{c}}{\sqrt{c}}\).
![]() How To: Rationalize the denominator of an expression with a monomial denominator
How To: Rationalize the denominator of an expression with a monomial denominator
- Multiply the numerator and denominator by the radical in the denominator.
- Simplify.
Sometimes, we will find the need to reduce, or cancel, after rationalizing the denominator.
Example \(\PageIndex{11}\): Rationalize a Denominator Containing a Single Term
Write in simplest form (rationalize the denominator).
| a. \( \dfrac{2\sqrt{3}}{3\sqrt{10}} \) | b. \(\dfrac { \sqrt { 2 } } { \sqrt { 5 x } }\) | c. \(\dfrac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } }\) |
a. The radical in the denominator is \(\sqrt{10}\). So multiply the fraction by \(\dfrac{\sqrt{10}}{\sqrt{10}}\). Then simplify.
\( \dfrac{2\sqrt{3}}{3\sqrt{10}}\times {\color{Cerulean}{ \dfrac{\sqrt{10}}{\sqrt{10}} } } = \dfrac{2\sqrt{30}}{30} = \dfrac{\sqrt{30}}{15} \)
b. The goal is to find an equivalent expression without a radical in the denominator. The radicand in the denominator determines the factors that you need to use to rationalize it. In this example, multiply by \(1\) in the form \(\frac { \sqrt { 5 x } } { \sqrt { 5 x } }\).
\(\begin{aligned} \frac { \sqrt { 2 } } { \sqrt { 5 x } } & = \frac { \sqrt { 2 } } { \sqrt { 5 x } } \cdot \color{Cerulean}{\frac { \sqrt { 5 x } } { \sqrt { 5 x } } }\\ & = \frac { \sqrt { 10 x } } { \sqrt { 25 x ^ { 2 } } } \quad\quad\: \color{Cerulean} { Simplify. } \\ & = \frac { \sqrt { 10 x } } { 5 x } \end{aligned}\)
c. In this example, we will multiply by \(1\) in the form \(\frac { \sqrt { 6 a b } } { \sqrt { 6 a b } }\).
\(\begin{aligned} \frac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } } & = \frac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } } \cdot \color{Cerulean}{\frac { \sqrt { 6 a b } } { \sqrt { 6 a b } }} \\ & = \frac { 3 a \sqrt { 12 a b } } { \sqrt { 36 a ^ { 2 } b ^ { 2 } } } \quad\quad\color{Cerulean}{Simplify.}\\ & = \frac { 3 a \sqrt { 4 \cdot 3 a b} } { 6 ab } \\ & = \frac { 6 a \sqrt { 3 a b } } { b }\quad\quad\:\:\color{Cerulean}{Cancel.} \\ & = \frac { \sqrt { 3 a b } } { b } \end{aligned}\)
Notice that \(b\) does not cancel in this example. Do not cancel factors inside a radical with those that are outside.
![]() Try It \(\PageIndex{11}\)
Try It \(\PageIndex{11}\)
Write in simplest form (rationalize the denominator).
| a. \(\dfrac{12\sqrt{3}}{\sqrt{2}}\) | b. \(\sqrt { \dfrac { 9 x } { 2 y } }\) |
- Answer
-
a. \(6\sqrt{6}\) \( \qquad \) b. \(\frac { 3 \sqrt { 2xy } } { 2 y }\)
Binomial Denominators
For a denominator containing the sum or difference of rational or irrational terms, multiply the numerator and denominator by the conjugate of the denominator, which is found by changing the sign that connects the two terms in the denominator. If the denominator is \(a+b\sqrt{c}\) , then the conjugate is \(a-b\sqrt{c}\).
![]() How to: Rationalize the denominator of an expression with a binomial denominator
How to: Rationalize the denominator of an expression with a binomial denominator
- Find the conjugate of the denominator.
- Multiply the numerator and denominator by the conjugate.
- Use the distributive property.
- Simplify.
Example \(\PageIndex{12}\): Rationalizing a Denominator Containing Two Terms
Write in simplest form (rationalize the denominator).
| a. \(\dfrac{4}{1+\sqrt{5}}\) | b. \(\dfrac { 1 } { \sqrt { 5 } - \sqrt { 3 } }\) | c. \(\dfrac { \sqrt { 10 } } { \sqrt { 2 } + \sqrt { 6 } }\) | d. \(\dfrac { \sqrt { x } - \sqrt { y } } { \sqrt { x } + \sqrt { y } }\) |
Solution
a. Begin by finding the conjugate of the denominator by writing the denominator and changing the sign. So the conjugate of \(1+\sqrt{5}\) is \(1-\sqrt{5}\). Then multiply the fraction by \(\tfrac{1-\sqrt{5}}{1-\sqrt{5}}\) .
\[\begin{align*} &\dfrac{4}{1+\sqrt{5}}\times { \color{Cerulean} { \dfrac{1-\sqrt{5}}{1-\sqrt{5}} } }\\[5pt] &\dfrac{4-4\sqrt{5}}{-4} & & \text{Use the distributive property}\\[5pt] &-1 + \sqrt{5} & & \text{Simplify} \end{align*}\]
b. In this example, the conjugate of the denominator is \(\sqrt { 5 } + \sqrt { 3 }\). Therefore, multiply by \(1\) in the form \(\frac { ( \sqrt { 5 } + \sqrt { 3 } ) } { ( \sqrt {5 } + \sqrt { 3 } ) }\).
\(\begin{aligned} \frac { 1 } { \sqrt { 5 } - \sqrt { 3 } } & = \frac { 1 } { ( \sqrt { 5 } - \sqrt { 3 } ) } \color{Cerulean}{\frac { ( \sqrt { 5 } + \sqrt { 3 } ) } { ( \sqrt { 5 } + \sqrt { 3 } ) } \:\:Multiply \:by\:"1".} \\ & = \frac { \sqrt { 5 } + \sqrt { 3 } } { \sqrt { 25 } + \sqrt { 15 } - \sqrt{15}-\sqrt{9} } \:\color{Cerulean}{Simplify.} \\ & = \frac { \sqrt { 5 } + \sqrt { 3 } } { 5-3 } \\ & = \frac { \sqrt { 5 } + \sqrt { 3 } } { 2 } \end{aligned}\)
Notice that the terms involving the square root in the denominator are eliminated by multiplying by the conjugate. We can use the property \(( \sqrt { a } + \sqrt { b } ) ( \sqrt { a } - \sqrt { b } ) = a - b\) to expedite the process of multiplying the expressions in the denominator.
c. Multiply by \(1\) in the form \(\frac { \sqrt { 2 } - \sqrt { 6 } } { \sqrt { 2 } - \sqrt { 6 } }\).
\(\begin{aligned} \frac{\sqrt{10}}{\sqrt{2}+\sqrt{6} }&= \frac{(\sqrt{10})}{(\sqrt{2}+\sqrt{6})} \color{Cerulean}{\frac{(\sqrt{2}-\sqrt{6})}{(\sqrt{2}-\sqrt{6})}\quad\quad Multiple\:by\:the\:conjugate.} \\ &= \frac { \sqrt { 20 } - \sqrt { 60 } } { 2 - 6 } \quad\quad\quad\quad\quad\quad\:\:\:\color{Cerulean}{Simplify.} \\ &= \frac { \sqrt { 4 \cdot 5 } - \sqrt { 4 \cdot 15 } } { - 4 } \\ &= \frac { 2 \sqrt { 5 } - 2 \sqrt { 15 } } { - 4 } \\ &=\frac{2(\sqrt{5}-\sqrt{15})}{-4} \\ &= \frac { \sqrt { 5 } - \sqrt { 15 } } { - 2 } = - \frac { \sqrt { 5 } - \sqrt { 15 } } { 2 } = \frac { - \sqrt { 5 } + \sqrt { 15 } } { 2 } \end{aligned}\)
d. In this example, we will multiply by \(1\) in the form \(\frac { \sqrt { x } - \sqrt { y } } { \sqrt { x } - \sqrt { y } }\).
\(\begin{aligned} \frac { \sqrt { x } - \sqrt { y } } { \sqrt { x } + \sqrt { y } } & = \frac { ( \sqrt { x } - \sqrt { y } ) } { ( \sqrt { x } + \sqrt { y } ) } \color{Cerulean}{\frac { ( \sqrt { x } - \sqrt { y } ) } { ( \sqrt { x } - \sqrt { y } ) } \quad \quad Multiply\:by\:the\:conjugate\:of\:the\:denominator.} \\ & = \frac { \sqrt { x ^ { 2 } } - \sqrt { x y } - \sqrt { x y } + \sqrt { y ^ { 2 } } } { x - y } \:\:\color{Cerulean}{Simplify.} \\ & = \frac { x - 2 \sqrt { x y } + y } { x - y } \end{aligned}\)
![]() Try It \(\PageIndex{12}\)
Try It \(\PageIndex{12}\)
Write in simplest form (rationalize the denominator).
| a. \(\dfrac{7}{2+\sqrt{3}}\) | b. \(\dfrac { 2 \sqrt { 3 } } { 5 - \sqrt { 3 } }\) |
- Answer
-
a. \(14-7\sqrt{3}\) \( \qquad \) b. \(\dfrac { 5 \sqrt { 3 } + 3 } { 11 }\)

