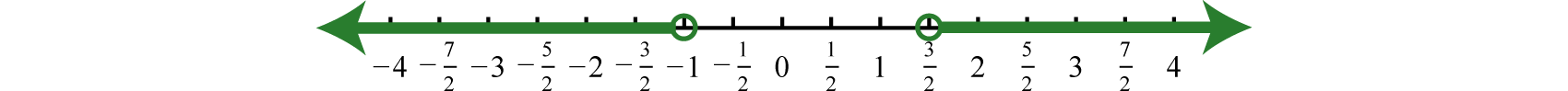0.8: Review - Linear Inequalities in One Variable
- Page ID
- 38277
Linear Inequalities
A linear inequality is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:
| \(5 x + 7 < 22\) | \(- 2 ( x + 8 ) + 6 \geq 20\) | \(- 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 )\) |
A solution to a linear inequality is a real number that will produce a true statement when substituted for the variable. Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation.
Example \(\PageIndex{1}\):
Are \(x=−4\) and \(x=6\) solutions to \(5x+7<22\)?
Solution
Substitute the values in for \(x\), simplify, and check to see if we obtain a true statement.
| Check \(x=4\): | Check \(x=6\): |
|---|---|
|
\(\begin{array} { r } { 5 ( \color{Cerulean}{- 4}\color{Black}{ )} + 7 < 22 } \\ { - 20 + 7 < 22 } \\ { - 13 < 22 } \:\:\color{Cerulean}{✓} \end{array}\) |
\(\begin{array} { c } { 5 ( \color{Cerulean}{6} \color{Black}{)} + 7 < 22 } \\ { 30 + 7 < 22 } \\ { 37 < 22 } \:\:\color{red}{✗} \end{array}\) |
Answer: \(x=−4\) is a solution and \(x=6\) is not
All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example:
\(\begin{array} { rll}
10 &> - 5 \\
10\color{Cerulean}{-7} & \color{Black}{>} -5\color{Cerulean}{-7} & \quad \color{Cerulean}{Subtract\: 7\: on\: both\: sides.} \\
3 &> - 12 \quad\color{Cerulean}{✓} & \quad\color{Cerulean}{True.} \\
10 &>-5 \\
\tfrac{10}{\color{Cerulean}{5}} &\color{Black}{>}\tfrac{-5}{\color{Cerulean}{5}} &\quad\color{Cerulean}{Divide\: both\: sides\: by\: 5.} \\
2 &>-1 \quad \color{Cerulean}{✓} & \quad\color{Cerulean}{True.}
\end{array}\)
Subtracting \(7\) from each side and dividing each side by positive \(5\) results in an inequality that is true.
Example \(\PageIndex{2}\):
Solve and graph the solution set: \(5x+7<22\).
Solution
\(\begin{array} { c } { 5 x + 7 < 22 } \\ { 5 x + 7 \color{Cerulean}{- 7}\color{Black}{ < 22}\color{Cerulean}{ - 7} } \\ { 5 x < 15 } \\ { \frac { 5 x } {\color{Cerulean}{ 5} } < \frac { 15 } { \color{Cerulean}{5} } } \\ { x < 3 } \end{array}\)

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect \(x=0\) to solve the original inequality and that \(x=5\) should not.
| Check \(x=0\): | Check \(x=5\): |
|---|---|
|
\(\begin{array} { r } { 5 ( \color{Cerulean}{0}\color{Black}{ )} + 7 < 22 } \\ { 7 < 22 }\:\:\color{Cerulean}{✓} \end{array}\) |
\(\begin{array} { r } { 5 ( \color{Cerulean}{5}\color{Black}{ )} + 7 < 22 } \\ { 25 + 7 < 22 } \\ { 32 < 22 } \:\:\color{red}{✗} \end{array}\) |
Checking in this manner gives us a good indication that we have solved the inequality correctly.
We can express this solution set in two ways: using set notation and interval notation.
\(\begin{array} { rl } { \{ x | x < 3 \} } &\color{Cerulean}{Set\: notation} \\ { ( - \infty , 3 ) } &\color{Cerulean}{Interval\: notation} \end{array}\)
In this text we will choose to present answers using interval notation.
Answer: \((−∞, 3) \)
When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement \(10 > −5\) and divide both sides by \(−5\).
\(\begin{array} { l } { 10 > - 5 } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5.} \\ { - 2 \color{red}{>}\color{Black}{ 1} \quad \color{red}{✗} \color{Cerulean}{ False } } \end{array}\)
Dividing by \(−5\) results in a false statement. To retain a true statement, the inequality must be reversed.
\(\begin{array} { l } { 10 \color{OliveGreen}{>}\color{Black}{ - 5} } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{<} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Reverse\: the\: inequality.} \\ { - 2 \color{OliveGreen}{<}\color{Black}{ 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ True } } \end{array}\)
The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality. It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions \(A\) and \(B\), where \(c\) is a positive nonzero real number, we have the following properties of inequalities:
| Addition property of inequalities: | If \(A<B\), then \(A \color{Cerulean}{+c}\:\color{Black}{<}\:B\color{Cerulean}{+c}\) |
|---|---|
| Subtraction property of inequalities: | If \(A<B\), then \(A \color{Cerulean}{-c}\:\color{Black}{<}\:B\color{Cerulean}{-c}\) |
| Multiplication property of inequalities: |
If \(A<B\), then \(\color{Cerulean}{c}\color{Black}{A}\:<\:\color{Cerulean}{c}\color{Cerulean}\color{Black}{B}\) \(\qquad\) If \(A<B\), then \(\color{Cerulean}{-c}\color{Black}{A}\:\color{OliveGreen}{>}\:\color{Cerulean}{-c}\color{Cerulean}\color{Black}{B}\) |
| Division property of inequalities: |
If \(A<B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black}{<}\frac{B}{\color{Cerulean}{c}}\) \(\qquad\)If \(A<B\), then \(\dfrac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\dfrac{\color{Black}{B}}{\color{Cerulean}{-c}}\) |
We use these properties to obtain an equivalent inequality, one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.
Example \(\PageIndex{3}\):
Solve and graph the solution set: \(−2(x+8)+6≥20\).
Solution
\(\begin{aligned} - 2 ( x + 8 ) + 6 & \geq 20 \quad\color{Cerulean}{Distribute.} \\ - 2 x - 16 + 6 & \geq 20 \quad\color{Cerulean}{Combine\: like\: terms.} \\ - 2 x - 10 & \geq 20 \quad\color{Cerulean}{Solve\: for\: x.} \\ - 2 x & \geq 30 \quad\color{Cerulean}{Divide\: both\: sides\: by\: -2.} \\ \frac { - 2 x } { \color{Cerulean}{- 2} } & \color{OliveGreen}{\leq} \frac { \color{Black}{30} } { \color{Cerulean}{- 2} } \quad\color{Cerulean}{Reverse\: the\: inequality.} \\ x & \leq - 15 \end{aligned}\)
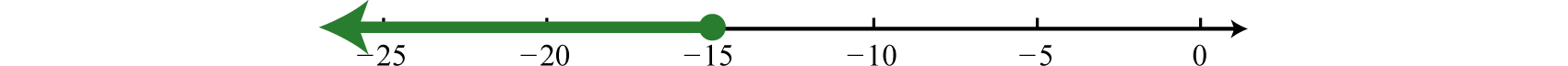
Answer: Interval notation \((−∞, −15] \)
Example \(\PageIndex{4}\):
Solve and graph the solution set: \(−2(4x−5)<9−2(x−2)\).
Solution
\(\begin{aligned} - 2 ( 4 x - 5 ) &< 9 - 2 ( x - 2 ) \\ - 8 x + 10 &< 9 - 2 x + 4 \\ - 8 x + 10 &< 13 - 2 x \\ - 6 x &< 3 \\
\frac { - 6 x } { \color{Cerulean}{- 6} } & {\color{OliveGreen}{>}} \frac { \color{Black}{3} } { \color{Cerulean}{- 6} } & {\color{Cerulean}{Reverse\:the\:inequality.}} \\
x &> - \frac { 1 } { 2 } \end{aligned}\)

Answer: Interval notation \((−\frac{1}{2}, ∞)\)
Example \(\PageIndex{5}\):
Solve and graph the solution set: \(\dfrac{1}{2}x−2≥\dfrac{1}{2}(\dfrac{7}{4}x−9)+1\).
Solution
\(\begin{aligned} \frac { 1 } { 2 } x - 2 &\geq \frac { 1 } { 2 } \left( \frac { 7 } { 4 } x - 9 \right) + 1 \\
\frac { 1 } { 2 } x - 2 &\geq \frac { 7 } { 8 } x - \frac { 9 } { 2 } + 1 \\
\frac { 1 } { 2 } x - \frac { 7 } { 8 } x &\geq - \frac { 7 } { 2 } + 2 \\
- \frac { 3 } { 8 } x &\geq - \frac { 3 } { 2 } \\
\left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left(\color{Black}{ - \frac { 3 } { 8 } x} \right) &\leq \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left( \color{Black}{-} \frac { 3 } { 2 } \right) &\quad \color{Cerulean} { Reverse\: the\: inequality. } \\
x &\leq 4 \end{aligned}\)

Answer: Interval notation: \((−∞, 4]\)
![]() Try It \(\PageIndex{5}\)
Try It \(\PageIndex{5}\)
Solve and graph the solution set: \(10 - 5 ( 2 x + 3 ) \leq 25\)
- Answer
-
\([ - 3 , \infty )\);

Compound Inequalities
Following are some examples of compound linear inequalities:
| \(- 13 < 3 x - 7 < 17\) | \(4 x + 5 \leq - 15 \text { or } 6 x - 11 > 7\) |
These compound inequalities are actually two inequalities in one statement joined by the word and or by the word or. For example,
\(- 13 < 3 x - 7 < 17\)
is a compound inequality because it can be decomposed as follows:
\(- 13 < 3 x - 7 \text { and } 3 x - 7 < 17\)
We can solve each inequality individually; the intersection of the two solution sets solves the original compound inequality. While this method works, there is another method that usually requires fewer steps. Apply the properties of this section to all three parts of the compound inequality with the goal of isolating the variable in the middle of the statement to determine the bounds of the solution set.
Example \(\PageIndex{6}\):
Solve and graph the solution set: \(−13<3x−7<17\).
Solution
\(\begin{array} { c } { - 13 < 3 x - 7 < 17 } \\ { - 13 \color{Cerulean}{+ 7}\color{Black}{ <} 3 x - 7 \color{Cerulean}{+ 7}\color{Black}{ <} 17 \color{Cerulean}{+ 7} } \\ { - 6 < 3 x < 24 } \\ { \frac { - 6 } { \color{Cerulean}{3} } \color{Black}{<} \frac { 3 x } { \color{Cerulean}{3} } \color{Black}{<} \frac { 24 } { \color{Cerulean}{3} } } \\ { - 2 < x < 8 } \end{array}\)

Answer: Interval notation: \((−2,8)\)
Example \(\PageIndex{7}\):
Solve and graph the solution set: \(\frac{5}{6}≤\frac{1}{3}(\frac{1}{2}x+4)<2\).
Solution
\(\begin{array} { c } { \frac { 5 } { 6 } \leq \frac { 1 } { 3 } \left( \frac { 1 } { 2 } x + 4 \right) < 2 } \\ { \frac { 5 } { 6 } \leq \frac { 1 } { 6 } x + \frac { 4 } { 3 } < 2 } \\ { \color{Cerulean}{6}\color{Black}{ \cdot} \left( \frac { 5 } { 6 } \right) \leq \color{Cerulean}{6}\color{Black}{ \cdot} \left( \frac { 1 } { 6 } x + \frac { 4 } { 3 } \right) < \color{Cerulean}{6}\color{Black}{ \cdot} ( 2 ) } \\ { 5 \leq x + 8 < 12 } \\ { 5 \color{Cerulean}{- 8}\color{Black}{ \leq} x + 8 \color{Cerulean}{- 8}\color{Black}{ <} 12 \color{Cerulean}{- 8} } \\ { - 3 \leq x < 4 } \end{array}\)

Answer: Interval notation \([−3,4)\)
It is important to note that when multiplying or dividing all three parts of a compound inequality by a negative number, you must reverse all of the inequalities in the statement. For example:
\(\begin{array} { c } { - 10 < - 2 x < 20 } \\ { \dfrac { - 10 } { \color{Cerulean}{- 2} } \color{OliveGreen}{>} \dfrac { \color{Black}{- 2 x} } { \color{Cerulean}{ - 2} } \color{OliveGreen}{>} \dfrac { \color{Black}{20} } { \color{Cerulean}{- 2} } } \\ { 5 > x > - 10 } \end{array}\)
The answer above can be written in an equivalent form, where smaller numbers lie to the left and the larger numbers lie to the right, as they appear on a number line.
\(- 10 < x < 5\)
Use interval notation, write: \((-10, 5)\)
![]() Try It \(\PageIndex{7}\)
Try It \(\PageIndex{7}\)
Solve and graph the solution set: \(−3≤−3(2x−3)<15\).
- Answer
-
\((-1,2]\);

For compound inequalities with the word “or” you work both inequalities separately and then consider the union of the solution sets. Values in this union solve either inequality.
Example \(\PageIndex{8}\):
Solve and graph the solution set: \(4x+5≤−15\) or \(6x−11>7\).
Solution
Solve each inequality and form the union by combining the solution sets.
\(\begin{array} { rlcrl }
4 x + 5 & \leq - 15 & & 6 x - 11 &>\; 7 \\
4 x & \leq - 20 & \qquad \text{ or } \qquad & 6 x &>\; 18 \\
x & \leq - 5 && x & \;> 3 \\
\end{array}\)
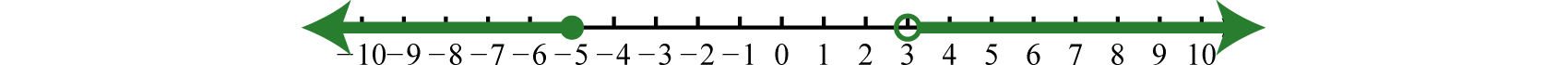
Answer: Interval notation \((−∞,−5]∪(3,∞)\)
![]() Try It \(\PageIndex{8}\)
Try It \(\PageIndex{8}\)
Solve and graph the solution set: \(5 ( x - 3 ) < - 20 \text { or } 2 ( 5 - 3 x ) < 1\).
- Answer
-
\(( - \infty , - 1 ) \cup \left( \frac { 3 } { 2 } , \infty \right)\)