1.7e: Exercises - Absolute Value
- Page ID
- 45456
A: Absolute Value Equations (I)
Exercise \(\PageIndex{A}\)
\( \bigstar \) Solve the following absolute value equations.
|
|
|
|
- Answers to odd exercises:
-
1. \(x = −3\) or \(x = 13\)
3. \(x = −7 \) or \( x = −1\)
5. \(x = −9 \) or \( x = 5\)
7. \(x=5\) or \(x=9\)9. \(x=8,\space x=0\)
11. \(x=7, \, x=1\)
13. \(x=1, \,x=−5\)
15. \(x=4, \space x=−\dfrac{2}{3}\)
17. \(x=−1,\space x=\dfrac{5}{2}\)
19. \(x = 0\) or \(x = 3\)21. \(x=−1, \,x=−\dfrac{5}{2}\)
23. no solution
25. \(x=1, \,x=−\dfrac{1}{2}\)
\( \bigstar \) Solve the following absolute value equations.
|
|
|
|
- Answers to odd exercises:
-
31. \(x=14, \,x=2\)
33. \(x = \frac{1}{2}, \; x = 1\)35. \(x = \frac{-32}{3}, \; x = 24\)
37. \(x = \frac{9}{2}, \; x = \frac{-21}{4} \)39. \(x = 0\), \(x = 6\)
41. \(x=−1, \,x=−\frac{2}{3}\)43. \(x=−3, \,x=3\)
45. \(x=−\frac{2}{7}, \; x=\frac{4}{3}\)47. \(x=3, x=\frac{1}{9}\)
49. \(x = 3, \; x = 5\)
B: Absolute Value Linear Inequalities (I)
Exercise \(\PageIndex{B}\): Absolute Value Linear Inequalities I
\( \bigstar \) Solve. State the solution in interval notation and graph the solution set on the number line.
|
|
|
|
- Answers to odd exercises:
-
51. \(( - 5,5 )\);

53. \([ - 4 , - 2 ]\);
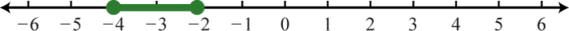
55. \(\emptyset\);
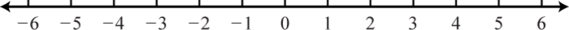
57. \([ - 1,4 ]\);

59. \(\left\{ \frac { 3 } { 5 } \right\}\);

61. \([ - 1,5 ]\);

63. \(( - \infty , - 5 ] \cup [ 5 , \infty )\);
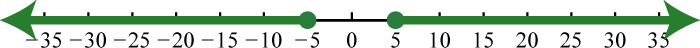
65. \(( - \infty , - 10 ) \cup ( 6 , \infty )\);
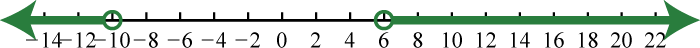
67. \(\mathbb { R }\);

69. \(( - \infty , - 2 ] \cup [ 7 , \infty )\);
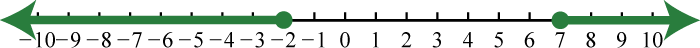
71. \(\left( - \infty , - \frac { 3 } { 2 } \right) \cup ( 3 , \infty )\);
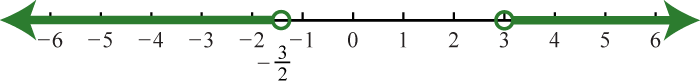
73. \(( - \infty , - 2 ) \cup ( 5 , \infty )\);
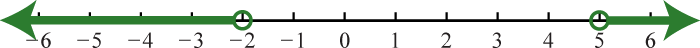
C: Absolute Value Linear Inequalities (II)
Exercise \(\PageIndex{C}\): Absolute Value Linear Inequalities II
\( \bigstar \) Solve. State the solution in interval notation and graph the solution set on the number line.
|
|
|
|
Answers to odd exercises:-
81. \(( - \infty , - 2 ) \cup ( 3 , \infty )\);
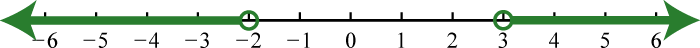
83. \(( 1,7 )\);

85. \(( - \infty , 3 ) \cup ( 5 , \infty )\);

87. \(( - \infty , - 8 ) \cup ( 3 , \infty )\);
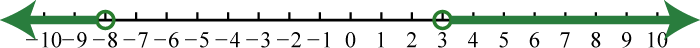
89. \(( - \infty , - 19 ] \cup [ - 6 , \infty )\);
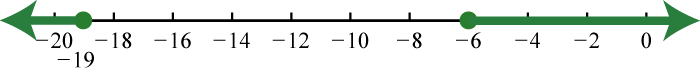
91. \(\mathbb { R }\);

93. \(\left[ \frac { 2 } { 3 } , 2 \right]\);

95. \(( - 12 , - 2 )\);
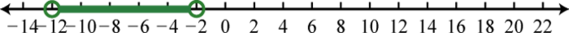
97. \(( - \infty , 0 ) \cup ( 6 , \infty )\);

99. \(\left( 0 , \frac { 1 } { 2 } \right)\);

101. \(\frac { 1 } { 2 }\);

103. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 2 } \right)\);

105. \([ 0,3 ]\);

107. \(( - \infty , 3 ) \cup ( 9 , \infty )\);


