2.1e: Exercises - Functions and Function Notation

A: Concepts

Exercise \(\PageIndex{A}\) 

 1) What is the difference between a relation and a function?
 2) What is the difference between the input and the output of a function?
 3) Why does the vertical line test tell us whether the graph of a relation represents a function?
 4) How can you determine if a relation is a one-to-one function?
 5) Why does the horizontal line test tell us whether the graph of a function is one-to-one?

Answers to odd exercises:

1. A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.

3. When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.

5. When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.

B: Determine if a set of points is a function

Exercise \(\PageIndex{B}\) 

\( \bigstar \) Determine whether the relation represents a function.

7) \(\{(3,4),(4,5),(5,6)\}\) 8) \(\{(−1,−1),(−2,−2),(−3,−3)\}\) 9) \( \{ (10,4), (-1,1), (-2,4), (4,9) \} \)

10) \( \{ (2,5),(7,11),(15,8),(7,9)\}\) 11) \( \{ (1,4), (1,5), (1,6) \} \) 12) \( \{ (4,1), (5,1), (6,1) \} \)

13) \(\{(a,b),(b,c),(c,c)\}\) 14) \(\{(a,b), (c,d), (a,c)\}\)

Answers to odd exercises:

7. function \( \qquad\) 9. function \( \qquad \) 11. not a function  \( \qquad\) 13. function.

C: Determine if an Equation is a function

Exercise \(\PageIndex{C}\) 

\( \bigstar \) Determine whether the relation represents \(y\) as a function of \(x\).

15) \(x+y = 25\) 16) \(5x+2y=10\) 16.1) \(|y| +x=2\) 16.2) \(|x|-y=-3\) 17) \(x=y^2\)

18) \(y=x^2\) 19) \(3x^2+y=14\) 20) \(2x+y^2=6\) 21) \(y=−2x^2+40x\) 22) \(x=y^2-8y+9\)

23) \(y^2=x^2\) 24) \(y^3=x^2\) 25) \(y=x^3\) 26) \(x=y^3\)

27) \(y=\dfrac{1}{x}\) 28) \(2xy=1\) 29) \(y=\dfrac{3x+5}{7x−1}\) 30) \(x=\dfrac{3y+5}{7y−1}\)

31) \(y=\pm\sqrt{1−x}\) 32) \(x=\pm\sqrt{1-y}\) 33) \(y=\sqrt{1−x^2}\) 34) \(x=\sqrt{1−y^2}\)

Answers to odd exercises:

15. function \( \qquad \) 17. not a function \( \qquad \) 19. function  \( \qquad \) 21. function \( \qquad\) 23. not a function \( \qquad \)
25. function \( \qquad \) 27. function \( \qquad \) 29. function \( \qquad \)  31. not a function \( \qquad\) 33. function 

D: Determine if a graph is a function (Vertical Line Test)

Exercise \(\PageIndex{D}\) 

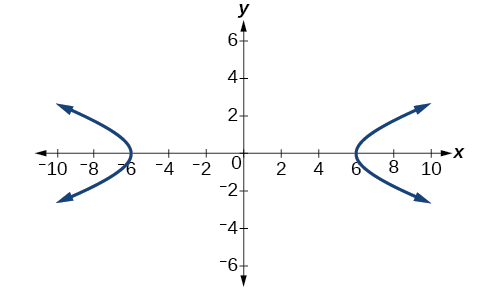
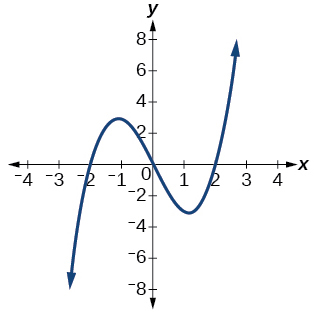
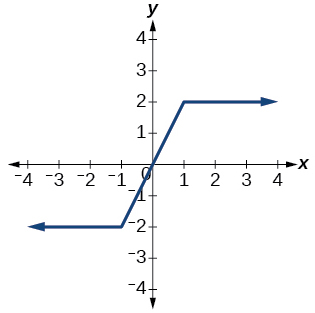
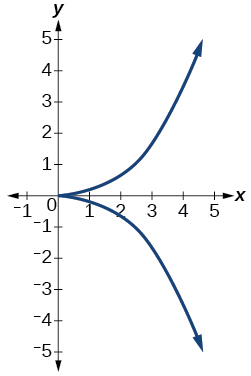
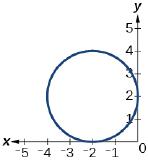
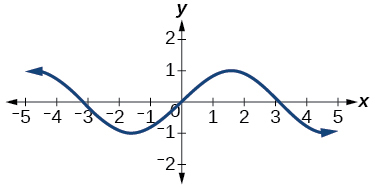
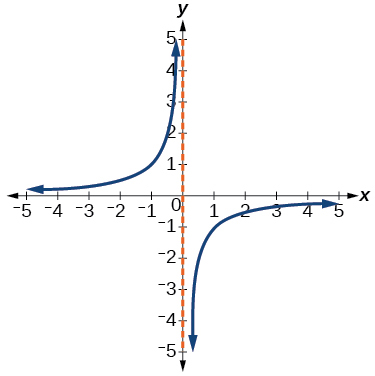
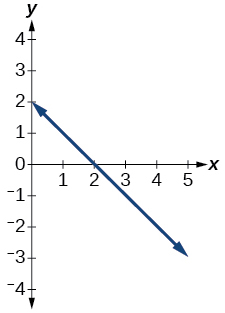
\( \bigstar \) Use the vertical line text to identify graphs in which \(y\) is a function of \( x \)

35) 36) 37) 38)

39) 40) 41)

42) 43) 44)

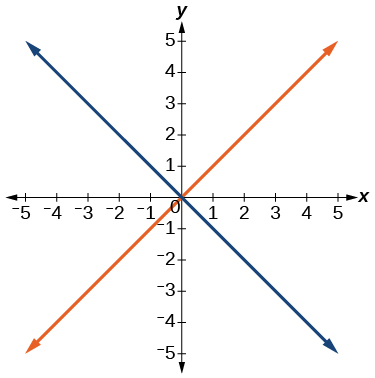45) 46) 47) 48)

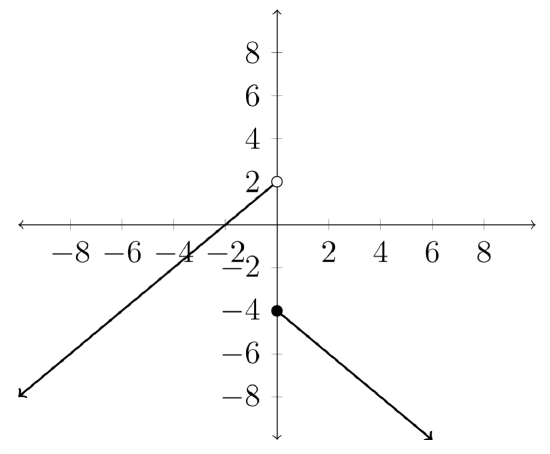Answers to odd exercises:

35. not a function \( \;\;\) 37. function  \( \;\; \) 39. not a function \( \;\;\) 41. function\( \;\;\) 43. function \( \;\; \) 45. function\( \;\; \) 47. function

E: Obtain Function Values from a formula

Exercise \(\PageIndex{E}\)

\( \bigstar \) Evaluate the function \(f\) at the values   a. \(f(−2)\),  b. \(f(−1)\),  c. \(f(0)\),  d. \(f(1)\), and  e. \(f(2)\).

49) \(f(x)=8−3x\) 50) \(f(x)=4−2x\)

51) \(f(x)=3+\sqrt{x+3}\) 52) \(f(x)=8x^2−7x+3\)

53) \(f(x)=3^x\) 54) \(f(x)=\dfrac{x-2}{x+3}\)

\( \bigstar \) Evaluate the function \(f\) at the values  a. \(f(−3)\),  b. \( f(2)\),  c. \(f(−a)\),  d. \(−f(a)\),  e. \( f(a+h)\).

55) \(f(x)=2x−5\) 56) \(f(x)=−5x^2+2x−1\)

57) \(f(x)=\sqrt{2−x}+5\) 58) \( f(x) = \sqrt{x^2+16}-3 \)

59) \(f(x)=|x−1|−|x+1|\) 60) \( f(x) = \dfrac{|x+3|}{x-3}\)

61) \( f(x) = \dfrac{x^2-1}{x+3}\) 62) \(f(x)=\dfrac{1-x}{5x+2}\)

\( \bigstar \) For the following exercises, find the values listed below for each function, if they exist, then simplify.
\( \quad \) a.  \(f(0)\),  b. \(f(1)\),  c. \(f(3)\),  d. \(f(−x)\),  e. \(f(a)\),  f. \(f(a+h)\)

63) \(f(x)=5x−2\) 64) \(f(x)=4x^2−3x+1\)

65) \(f(x)=\dfrac{2}{x}\) 66) \(f(x)=|x−7|+8\)

67) \(f(x)=\sqrt{6x+5}\) 68) \(f(x)=\dfrac{x−2}{3x+7}\)

69) \(f(x)=9\)

Answers to odd exercises:

49. a. \(f(−2)=14\);  b. \(f(−1)=11\);  c. \(f(0)=8\);  d. \(f(1)=5\);  e. \(f(2)=2\)
51. a. \(f(−2)=4\);   b. \(f(−1)=4.414\);   c. \(f(0)=4.732\);   d. \(f(1)=5\);   e. \(f(2)=5.236\)
53. a. \(f(−2)=\frac{1}{9}\);   b. \(f(−1)=\frac{1}{3}\);   c. \(f(0)=1\);   d. \(f(1)=3\);   e. \(f(2)=9\)
55. a. \(f(−3)=−11\); b. \(f(2)=−1\); c. \(f(−a)=−2a−5\); d. \(−f(a)=−2a+5\); e. \(f(a+h)=2a+2h−5\)
57. a. \(f(−3)=\sqrt{5}+5\);   b. \(f(2)=5\);   c. \(f(−a)=\sqrt{2+a}+5\);   d. \(−f(a)=−\sqrt{2−a}−5\);  
     e. \(f(a+h)=\sqrt{2−a−h}+5\)
59. a. \(f(−3)=2\);   b. \(f(2)=1−3=−2\);   c. \(f(−a)=|−a−1|−|−a+1|\);  
     d. \(−f(a)=−|a−1| +|a+1|\);   e. \(f(a+h)= |a+h−1|−|a+h+1|\)
61. a. \(f(−3)=\text{undefined} \);  b. \(f(2)=\frac{3}{5}\); c. \(f(−a)=\frac{a^2-1}{3-a}\); d. \(−f(a)=−\frac{a^2-1}{a+3} \); e. \(f(a+h)=\frac{a^2+2ah+h^2-1}{a+h+3}\)
63) a. \(−2\)   b. \(3\)   c. \(13\)   d. \(−5x−2\)   e. \(5a−2\)   f. \(5a+5h−2\)
65) a. Undefined   b. \(2\)   c. \(\frac{2}{3}\)   d. \(−\frac{2}{x}\)   e. \(\frac{2}{a}\)   f. \(\frac{2}{a+h}\)
67) a. \(\sqrt{5}\)   b. \(\sqrt{11}\)   c. \(\sqrt{23}\)   d. \(\sqrt{−6x+5}\)   e. \(\sqrt{6a+5}\)   f. \(\sqrt{6a+6h+5}\)
69) a. 9   b. 9   c. 9   d. 9   e. 9   f. 9

F: Determine a function's input or output

Exercise \(\PageIndex{F}\)

\( \bigstar \) Determine the following function values.

71) Given the relation \(3r+2t=18\). a. Write the relation as a function \(r=f(t)\). b. Evaluate \(f(−3)\). c. Solve \(f(t)=2\).   72) Given the function \(k(t)=2t−1\): a. Evaluate \(k(2)\). b. Solve \(k(t)=7\).

73) Given the function \(f(x)=8−3x\): a. Evaluate \(f(−2)\). b. Solve \(f(x)=−1\).   74) Given the function \(p(c)=c^2+c\): a. Evaluate \(p(−3)\). b. Solve \(p(c)=2\).

75) Given the function \(f(x)=x^2−3x\): a. Evaluate \(f(5)\). b. Solve \(f(x)=4\).   76) Given the function \(f(x)=\sqrt{x+2}\): a. Evaluate \(f(7)\). b. Solve \(f(x)=4\).

Answers to odd exercises:

71. a. \(f(t)=6−\frac{2}{3}t\); b. \(f(−3)=8\); c. \(t=6\)  73. a. \(f(−2)=14\); b. \(x=3\)   75. a. \(f(5)=10\); b. \(x=−1\) or \(x=4\)

G: Obtain Function Values from a Graph

Exercise \(\PageIndex{G}\) 

\( \bigstar \) Use the graph of \(f\) to find each indicated function value.

79) Given the following graph, 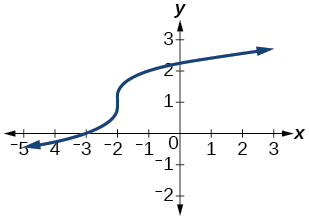Evaluate \(f(0)\). Solve for \(f(x)=0\).		80) Given the following graph, Evaluate \(f(−1)\). Solve for \(f(x)=3\).

 

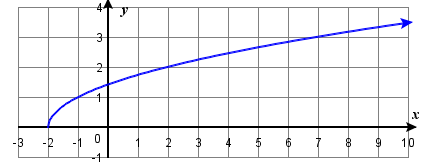81) Given the following graph, Evaluate \(f(0)\). Solve for \(f(x)=−3\).

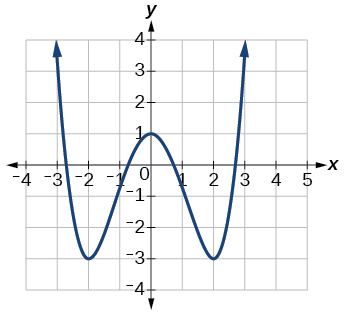82) Given the following graph, Evaluate \(f(4)\). Solve for \(f(x)=1\).

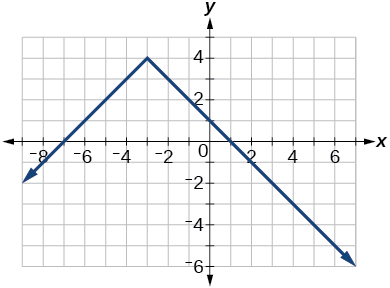Answers to odd exercises:

79. a.\(f(0) \approx 2.3\); b. \(f(x)=0\), \(x=−3\)  \(\quad\)  81. a.\(f(0)=1\); b. \(f(x)=−3\), \(x=−2\) or \(x=2\)

H: Evaluate Difference Quotients 

Exercise \(\PageIndex{H}\) 

\( \bigstar \) Find and simplify the difference quotient \(\dfrac{f(x+h) - f(x)}{h} \) for the given function. Simplify so \(h\) is not a factor in the denominator. This may involve simplifying complex fractions or rationalizing the numerator.

\( f(x) = 2x - 5 \)  \( f(x) = -3x + 5 \) \( f(x) = 6 \) \( f(x) = 3x^2 - x \) \( f(x) = -x^2 + 2x - 1 \) \( f(x) = 4x^2 \) \( f(x) = x-x^2 \) \( f(x) = x^{3} + 1 \) \( f(x) = mx + b\; \) where \( m \neq 0 \) \( f(x) = ax^{2} + bx + c\; \) where \( a \neq 0 \)

\( f(x) = \dfrac{2}{x} \) \( f(x) = \dfrac{3}{1-x} \) \( f(x) = \dfrac{1}{x^2} \) \( f(x) = \dfrac{2}{x+5} \) \( f(x) = \dfrac{1}{4x-3} \) \( f(x) = \dfrac{3x}{x+1} \) \( f(x) = \dfrac{x}{x - 9} \)

\( f(x) = \dfrac{x^2}{2x+1} \) \( f(x) = \sqrt{x-9} \) \( f(x) = \sqrt{2x+1} \) \( f(x) = \sqrt{-4x+5} \) \( f(x) = \sqrt{4-x} \) \( f(x) = \sqrt{ax+b} \) , where \( a \neq 0 \) . \( f(x) = x \sqrt{x} \) \( f(x) = \sqrt[3]{x} \) . \( \textbf{HINT:}  (a-b)\left(a^2+ab+b^2\right) = a^3 - b^3 \) \(g(x)=5−x^2\)

109) Given the function \(g(x)=x^2+2x\), evaluate \(\dfrac{g(x)−g(a)}{x−a}\), \(x{\neq}a\) and simplify.

Answers to odd exercises:

83. \( 2 \) 85. \( 0 \) 87. \( -2x-h+2 \) 89. \( -2x-h+1 \) 91. \( m \) 93. \( \dfrac{-2}{x(x+h)} \)

95. \( \dfrac{-(2x+h)}{x^2(x+h)^2} \) 97. \( \dfrac{-4}{(4x-3)(4x+4h-3)} \) 99. \( \dfrac{-9}{(x - 9)(x + h - 9)} \) 101. \( \dfrac{1}{\sqrt{x+h-9} + \sqrt{x-9}} \)

103. \( \dfrac{-4}{\sqrt{-4x-4h+5} + \sqrt{-4x+5}} \) 105. \( \dfrac{a}{\sqrt{ax+ah+b} + \sqrt{ax+b}} \) 107. \( \dfrac{1}{(x+h)^{2/3} + (x(x+h))^{1/3} + x^{2/3}} \) 109. \(\dfrac{g(x)−g(a)}{x−a}=x+a+2\), \(x{\neq}a\)