2.1: Functions and Function Notation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Determine whether a relation represents a function algebraically and graphically
- Use function notation to evaluate functions given a formula or a graph
- Us a graph or formula to find input function values that will produce a given output
- Evaluate and simplify difference quotients
Determine Whether a Relation Represents a Function
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1} \nonumber
The domain is \{1, 2, 3, 4, 5\}. The range is \{2, 4, 6, 8, 10\}.
Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letter x. Each value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter y.
A function f is a relation that assigns each value in the domain of a function to a single value in the range to a value in the domain. In other words, no x-value is assigned to more than one y-value. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, {1, 2, 3, 4, 5}, is paired with exactly one element in the range, \{2, 4, 6, 8, 10\}.
Consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
\mathrm{\{(odd, 1), (even, 2), (odd, 3), (even, 4), (odd, 5)\}}
Notice that each element in the domain, {even, odd} is not paired with exactly one element in the range, \{1, 2, 3, 4, 5 \}. For example, the term “odd” corresponds to three values from the domain, \{1, 3, 5 \}, and the term “even” corresponds to two values from the range, \{2, 4\}. This violates the definition of a function, so this relation is not a function.
Figure \PageIndex{} compares relations that are functions and not functions.
![[Three relations that demonstrate what constitute a function.]](https://math.libretexts.org/@api/deki/files/46034/CNX_Precalc_Figure_01_01_001.jpg?revision=1&size=bestfit&width=898&height=224)
Definition: Function, Domain, Range
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.
Often in equations, the input values are x values, the output values are y values and "y is a function of x."
![]() Howto: Determine whether a relationship between two quantities is a function.
Howto: Determine whether a relationship between two quantities is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, then "the output is a function of the input", and the relationship is classified as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
Practical Examples of Functions
Example \PageIndex{1}: Determining If Menu Price Lists Are Functions
The coffee shop menu, shown in Figure \PageIndex{1} consists of items and their prices.
- Is price a function of the item?
- Is the item a function of the price?

Solution
- Let’s begin by considering the input as the items on the menu. The output values are then the prices. See below.
![[A menu of donut prices from a coffee shop where a plain donut is $1.49 and a jelly donut and chocolate donut are $1.99.]](https://math.libretexts.org/@api/deki/files/46020/CNX_Precalc_Figure_01_01_027.v2.jpg?revision=1)
Each item on the menu has only one price, so the price is a function of the item.
- Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it. See below.
![[Association of the prices to the donuts.]](https://math.libretexts.org/@api/deki/files/46018/CNX_Precalc_Figure_01_01_028.jpg?revision=1)
Therefore, the item is a not a function of price.
Example \PageIndex{2}: Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? Table \PageIndex{2} shows a possible rule for assigning grade points.
| Percent grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Grade point average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Solution
For any percent grade earned, there is just one associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.
In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
![]() Try It \PageIndex{2}
Try It \PageIndex{2}
The table below lists the five greatest baseball players of all time in order of rank.
| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
- Answer a
-
Yes
- Answer b
-
yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
Determine if an Equation is a Function
In order to be a function, each element in the domain can correspond to just a single value in the range. When there exists an element in the domain that corresponds to two (or more) different values in the range, the relation is not a function. In the case of equations, if an equation is solved for y and the result is that for some value of x, multiple different values of y can be obtained from that single value for x, then the equation does not define y as a function of x.
![]() Howto: Determine if an equation defines a function.
Howto: Determine if an equation defines a function.
Given an equation in two variables, for example, x and y.
- Solve the equation for y.
- If more than one value of y can be obtained for a given x, then the equation does not define y as a function of x. One example is if an equation is obtained that looks like y = \pm .....
Example \PageIndex{3A}
Express the relationship 2n+6p=12 as a function of n, if possible.
Solution: To express the relationship as a function of n, the equation needs to be rewritten in the form p=[expression involving n].
\begin{align*}2n+6p&=12 \\ 6p&=12−2n & \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & \text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}
From this result, we can see that for each value of n there is one and only one value for p, so therefore the equation defines p as a function of n
Example \PageIndex{3B}
Does the equation x^2+y^2=1 represent a function of x?
Solution First we subtract x^2 from both sides. Then solve for y.
y^2=1−x^2 \nonumber
y=\pm\sqrt{1−x^2} \nonumber
=+\sqrt{1−x^2}\;\text{and}\;−\sqrt{1−x^2} \nonumber
Since more than a single value for y can be obtained for a given value of x, the equation is not a function of x
![]() Try It \PageIndex{3}
Try It \PageIndex{3}
Do the following equations represent functions of x?
| a. x−8y^3=0 | b. | y +3 | = 4 - x | c. x + 8 = \sqrt{y + 1} |
|
|
|
 Are there relationships expressed by a equation that do represent a function but which still cannot be represented by an algebraic formula ?
Are there relationships expressed by a equation that do represent a function but which still cannot be represented by an algebraic formula ?
Determine if a graph represents a function
Functions can be represented by equations; they can also be represented as a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value x and the output y, and we say y is a function of x, or y=f(x) when the function is named f. The graph of the function is the set of all points (x,y) in the plane that satisfies the equation y=f(x). If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. For example, the black dots on the graph of a polynomial in the figure below tell us that f(0)=2 and f(6)=1. However, the set of all points (x,y) satisfying y=f(x) is a curve. The curve shown includes (0,2) and (6,1) because the curve passes through those points
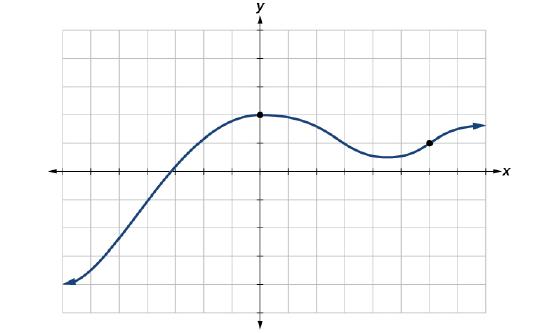
Graph of a polynomial.
Definition: The Vertical Line Test
The Vertical Line Test is a test used to determine if a graph represents a function. If there is no vertical line that crosses a graph in more than one point, the graph is a function.
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. These ideas are illustrated in the figure below.
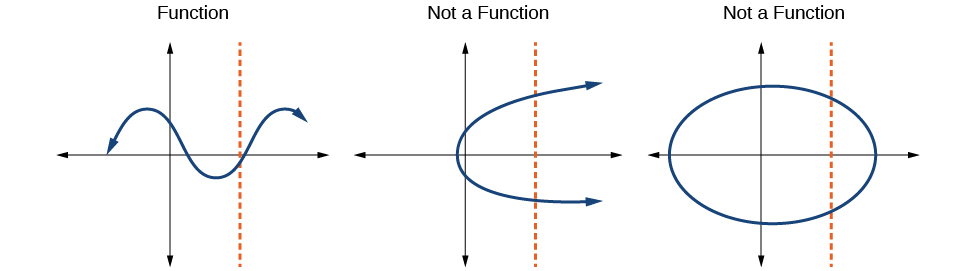
![]() Howto: Use the vertical line test to determine if a graph represents a function.
Howto: Use the vertical line test to determine if a graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, the graph does not represent a function.
Example \PageIndex{4}: Applying the Vertical Line Test
Which of the graphs in Figure \PageIndex{4} represent(s) a function?
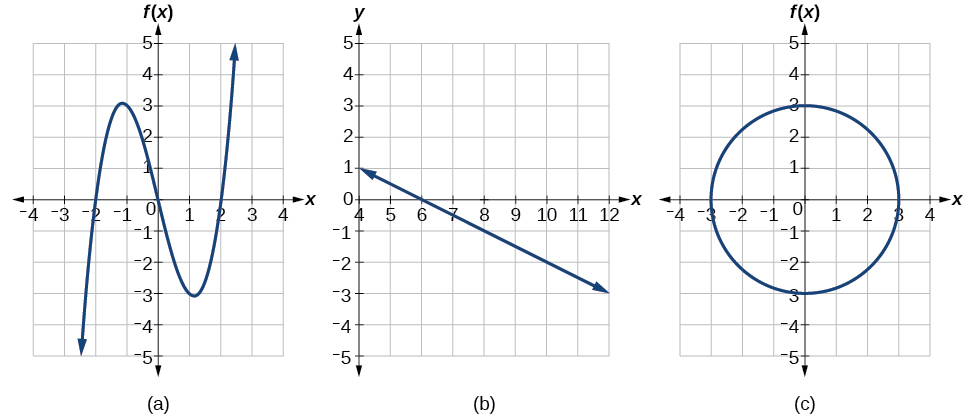
Figure \PageIndex{4}: Graph of a polynomial (a), a downward-sloping line (b), and a circle (c).
Solution
If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of Figure \PageIndex{4}. From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x-values, a vertical line would intersect the graph at more than one point, as shown in Figure \PageIndex{4c}.
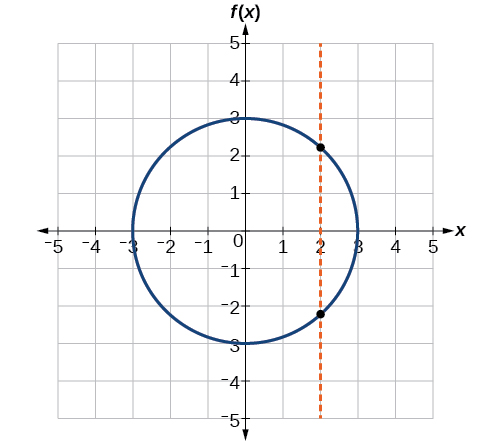
Figure \PageIndex{4c}: Graph of a circle.
![]() Try It \PageIndex{4}
Try It \PageIndex{4}
Does the graph of an absolute value function in the figure below represent a function?
![[Absolute function f(x)=|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg?revision=1&size=bestfit&width=288&height=256)
Graph of an absolute value function.
- Answer
-
yes
Function Notation and Evaluation
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables h for height and a for age. The letters f, g, and h are often used to represent functions just as we use x, y, and z to represent numbers and A, B, and C to represent sets.
\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array} \nonumber
Remember, we can use any letter to name the function; the notation h(a) shows us that h depends on a. The value a must be put into the function h to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For example f(a+b) means “first add a and b, and the result is the input for the function f.” The operations must be performed in this order to obtain the correct result.
Definition: Function Notation
The notation y=f(x) defines a function named f. This is read as “y is a function of x.” The letter x represents the input value, or independent variable. The letter y, or f(x), represents the output value, or dependent variable.
Example \PageIndex{5A}: Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.
Solution
Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.
The number of days in a month is a function of the name of the month, so if we name the function f, we write \mathrm{days}=f(\mathrm{month}) or d=f(m). The name of the month is the input to a “rule” that associates a specific number (the output) with each input.
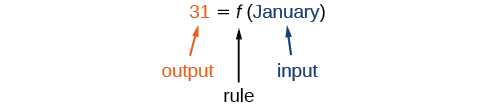
For example, f(\mathrm{March})=31, because March has 31 days. The notation d=f(m) reminds us that the number of days, d (the output), is dependent on the name of the month, m (the input).
Analysis
Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.
Example \PageIndex{5B}: Interpreting Function Notation
A function N=f(y) gives the number of police officers, N, in a town in year y. What does f(2005)=300 represent?
Solution
When we read f(2005)=300, we see that the input year is 2005. The value for the output, the number of police officers (N), is 300. Remember, N=f(y). The statement f(2005)=300 tells us that in the year 2005 there were 300 police officers in the town.
![]() Try It \PageIndex{5}
Try It \PageIndex{5}
Use function notation to express the weight of a pig in pounds as a function of its age in days d.
- Answer
-
w=f(d)
 Instead of a notation such as y=f(x), could we use something like y=y(x), meaning "y is a function of x?"
Instead of a notation such as y=f(x), could we use something like y=y(x), meaning "y is a function of x?"
Evaluate a Function Given a Formula
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function f(x)=5−3x^2 can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
![]() Howto: Evaluate a function given its formula.
Howto: Evaluate a function given its formula.
Given the formula for a function, evaluate.
- Replace the input variable in the formula with the value provided.
- Calculate the result.
Example \PageIndex{6A}: Evaluate a polynomial function
Evaluate f(x)=x^2+3x−4 at \qquad a. 2 \qquad b. a \qquad c. a+5
Solution
Replace the x in the function with each specified value.
a. Because the input value is a number, 2, we can use simple algebra to simplify.
\begin{align*}f( {\color{Cerulean}{2}} )&=( {\color{Cerulean}{2}} )^2+3( {\color{Cerulean}{2}} )−4\\&=4+6−4\\ &=6\end{align*}
b. In this case, the input value is a letter so we cannot simplify the answer any further.
f( {\color{Cerulean}{a}} )=( {\color{Cerulean}{a}} )^2+3( {\color{Cerulean}{a}} )−4 \nonumber
c. With an input value of a+5, we must use the distributive property.
\begin{align*}f( {\color{Cerulean}{a+5}} )&=(a+5)( {\color{Cerulean}{a+5}} )^2+3( {\color{Cerulean}{a+5}} )−4\\&=a^2+2a(5)+5^2+3a+15−4\\&=a^2+13a+36 \end{align*}
Example \PageIndex{6B}
For the function g(x)=3x−5, evaluate the function. \qquad a. g(h^2+1) \qquad b. g(x+2)
Solution
a.
\begin{array}{rll} g( {\color{Cerulean}{h^2+1}} )&=3( {\color{Cerulean}{h^2+1}} )−5 & \text{To evaluate } g(h^2+1) \text{, substitute } h^2+1 \text{ for }x\\ &= 3h^2+3-5 & \text{Simplify.}\\ &= 3h^2-2 \end{array}
b.
\begin{array}{rll} g( {\color{Cerulean}{x+2}} )&=3( {\color{Cerulean}{x+2}} )−5 & \text{To evaluate } g(x+2) \text{, substitute } x+2 \text{ for }x\\ &= 3x+6-5 & \text{Simplify.}\\ &= 3x+1 \end{array}
Example \PageIndex{6C}: Evaluate a function containing radicals
For the function f(x)=\sqrt{2x-1}, find \qquad a. f(5) \qquad b. \qquad f(-2) \qquad c. f(8x^2+5)
Solution:
a.
\begin{array}{rll} f(5)( {\color{Cerulean}{5}} )&=\sqrt{2 \cdot ( {\color{Cerulean}{5}} )-1} & \text{To evaluate } f(5) \text{, substitute } 5 \text{ for }x\\ &= \sqrt{9} & \text{Simplify.}\\ &= 3 &\text{Take the square root.} \end{array}
b.
\begin{array}{rll} f( {\color{Cerulean}{-2}} )&=\sqrt{2( {\color{Cerulean}{-2}} )-1} & \text{To evaluate } f(-2) \text{, substitute } -2 \text{ for }x\\ &= \sqrt{-5} & \text{Simplify.}\\ &= i\sqrt{5} &\text{Take the square root. }\\ & &\text{This function does not have a real number value at }x = 2. \end{array}
c.
\begin{array}{rll} f( {\color{Cerulean}{5}} )&=\sqrt{2(8x^2+( {\color{Cerulean}{5}} ))-1} & \text{To evaluate } f(8x^2+5) \text{, substitute } 8x^2+5 \text{ for }x\\ &= \sqrt{16x^2+10-1} & \text{Simplify.}\\ &= \sqrt{16x^2+9} &\text{This expression cannot be further simplified!!} \end{array}
Example \PageIndex{6D}: Evaluate a rational function
For the function f(x)=\dfrac{2-x}{x^2-1}, find \qquad a. f(4) \qquad b. f(1) \qquad c. f(x+3)
Solution:
a.
\begin{array}{rll} f( {\color{Cerulean}{4}} )&=\dfrac{2-( {\color{Cerulean}{4}} )}{( {\color{Cerulean}{4}} )^2-1} & \text{To evaluate } f(4) \text{, substitute } 4 \text{ for }x\\ &= \dfrac{-2}{15} & \text{Simplify.}\\ \end{array}
b.
\begin{array}{rll} f( {\color{Cerulean}{1}} )&=\dfrac{2- {\color{Cerulean}{1}} }{( {\color{Cerulean}{1}} )^2-1} & \text{To evaluate } f(1) \text{, substitute } 1 \text{ for }x\\ &= \dfrac{1}{0} & \text{Simplify.}\\ &= \text{Undefined} &\text{This function is undefined at }x = 1. \end{array}
c.
\begin{array}{rll} f( {\color{Cerulean}{x+3}} )&=\dfrac{2-( {\color{Cerulean}{x+3}} )}{( {\color{Cerulean}{x+3}} )^2-1} & \text{To evaluate } f(x+3) \text{, substitute } (x+3) \text{ for }x\\ &= \dfrac{2-x-3}{x^2+6x+9-1} & \text{Simplify.}\\ &= \dfrac{-x-1}{x^2+6x+8} &\text{Simplify (factor)}\\ &=- \dfrac{x+1}{(x+2)(x+4)} \end{array}
![]() Try It \PageIndex{6}: Evaluate functions
Try It \PageIndex{6}: Evaluate functions
Given f(x)=\sqrt{3 x-2}, g(x)=4x−7 and h(x)=\dfrac{|x-3|}{x^2+x^3+1} , evaluate the following. Simplify.
a. f(6) \qquad b. f(0) \qquad c. g(m^2) \qquad d. g(x−3) \qquad e. h(2) \qquad f. h(-x)
- Answer
- a. f(6)=4 \quad b. f(0)=i\sqrt{2} \quad c. 4m^2−7 \quad d. 4x−19 \quad e. h(2)=\dfrac{1}{13} \quad f. h(-x)= \dfrac{|x+3|}{x^2-x^3+1}
Evaluate a Function Given a Graph
Evaluating a function using a graph requires finding the corresponding output value for a given input value. We find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).
Example \PageIndex{7}: Reading Function Values from a Graph
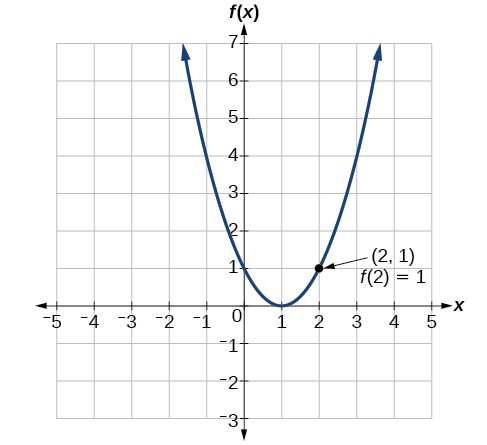
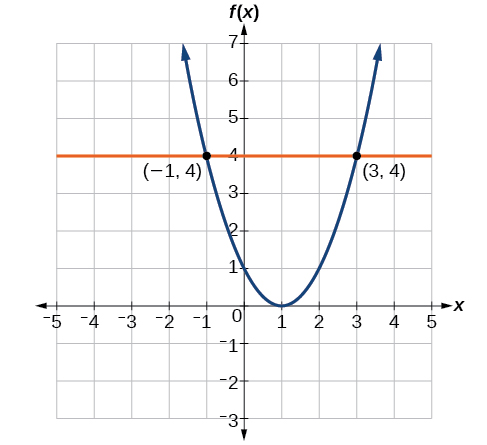
Given the graph in Figure \PageIndex{7}, \qquad a. Evaluate f(2). \qquad b. For what values of x is f(x)=4?
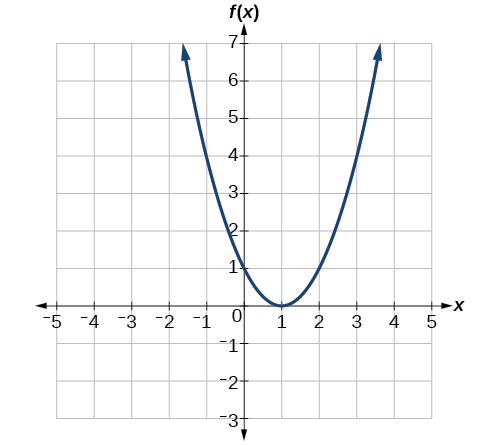
Figure \PageIndex{7}: Graph of a positive parabola centered at (1, 0).
Solution
a. To evaluate f(2), locate the point on the curve where x=2, then read the y-coordinate of that point. The point has coordinates (2,1), so f(2)=1. See Figure \PageIndex{7a}.
b. To find what values of x have a y-coordinate of 4, examine where the horizontal line y=4 intersects the graph. We locate two points of the curve with output value 4: (−1,4) and (3,4). This means f(−1)=4 and f(3)=4 and the two x values that have a y-coordinate of 4 are x=−1 or x=3. These points also represent the two solutions to f(x)=4:See Figure \PageIndex{7b}.
|
\PageIndex{7a}: Graph of a positive parabola centered at (1, 0) |
Figure \PageIndex{7b}: Graph of an upward-facing parabola with a vertex at (0,1) and labeled points at (-1, 4) and (3,4). A line at y = 4 intersects the parabola at the labeled points. |
![]() Try It \PageIndex{7}
Try It \PageIndex{7}
Given the graph in Figure \PageIndex{7}, for what values of x is f(x)=1?
- Answer
-
x=0 or x=2
Find a function's input value given its output value and its formula
When we know an output value and want to determine the input values that would produce that output value algebraically, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Example \PageIndex{8}: Solving Functions
Given the function h(p)=p^2+2p, solve for h(p)=3.
Solution
\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\\ \begin{array}{c|c} p+3=0 & p-1=0\\ p=-3 & p=1 \end{array} &\text{Use zero factor property to solve} \end{array}
This gives us two solutions. The output h(p)=3 when the input is either p=1 or p=−3. We can also verify by graphing as shown in Figure \PageIndex{8}. The graph verifies that h(1)=h(−3)=3.
![[Graph of a parabola with labeled points (-3, 3), (1, 3), and (4, 24).]](https://math.libretexts.org/@api/deki/files/868/CNX_Precalc_Figure_01_01_006.jpg?revision=1&size=bestfit&width=287&height=270)
Figure \PageIndex{8}: Graph of h(p)=p^2+2p
![]() Try It \PageIndex{8}
Try It \PageIndex{8}
Given the function g(m)=\sqrt{m−4}, solve g(m)=2.
- Answer
-
m=8
Difference Quotients
An important concept in calculus involves at looking at a quantity called the difference quotient which measures the average rate of change of a function over an interval, and is used to find the slope of a function at a point on its graph.
Example \PageIndex{9A}: Evaluate the difference quotient
Evaluate \dfrac{f(a+h)−f(a)}{h} given f(x)=x^2+3x−4
Solution
Replace the x in the function with each specified value.
Evaluate f(a+h). The distributive property must be used.
\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}
Evaluate f(a)
f(a)=a^2+3a−4\nonumber
Now combine the results and simplify.
\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} \qquad\qquad \text{Factor out }h.\\ &=2a+h+3 \quad\qquad\qquad \text{Simplify.}\end{align*}
Example \PageIndex{9B}: Evaluating the Difference Quotient
1. Evaluate the difference quotient \dfrac{f(x+h)-f(x)}{h} for the following functions. In all cases simplify so that the denominator does not have a factor of h.
a. f(x)=2x^2-3x
\begin{align*}\dfrac{f(x+h)−f(x)}{h}&=\dfrac{(2(x+h)^2-3(x+h)) -( 2x^2-3)}{h} && \text{Substitute.}\\ &=\dfrac{(2x^2+4xh+2h^2 -3x-3h) -2x^2+3x}{h} && \text{Multiply out numerator.}\\ &=\dfrac{4xh +2h^2-3h}{h} && \text{Combine like terms.}\\ &=4x+2h-3 && \text{Cancel}\end{align*}
b. f(x)=\dfrac{x}{x-2}. Simplify the complex fraction.
\begin{align*}\dfrac{f(x+h)−f(x)}{h}&=\dfrac{ \dfrac{x+h}{x+h-2} - \dfrac{x}{x-2} }{h}\\ &=\dfrac{\dfrac{x+h}{x+h-2}-\dfrac{x}{x-2}}{h}\cdot \dfrac{(x+h-2)(x-2)}{(x+h-2)(x-2)} && \text{Multiply by a convenient 1}\\[5pt] &=\dfrac{(x+h)(x-2)-x(x+h-2)}{h(x+h-2)(x-2)} && \text{Multiply.}\\[5pt] &=\dfrac{x^2-2x+hx-2h-x^2-xh+2x}{h(x+h-2)(x-2)} && \text{Multiply out numerator.}\\[5pt] &=\dfrac{-2h}{h(x+h-2)(x-2)} && \text{Combine like terms.}\\ &=\dfrac{-2}{(x+h-2)(x-2)} && \text{Cancel}\end{align*}
c. f(x)=\sqrt{5x+1}. Rationalize the numerator.
\begin{align*}\dfrac{f(x+h)−f(x)}{h}&=\dfrac{ \sqrt{5(x+h)+1} - \sqrt{5x+1} }{h}\\ &=\dfrac{ \sqrt{5(x+h)+1} - \sqrt{5x+1} }{h} \cdot \dfrac{\sqrt{5(x+h)+1} + \sqrt{5x+1} }{ \sqrt{5(x+h)+1} + \sqrt{5x+1} }&& \text{Rationalize the numerator} \\ &=\dfrac{5x+5h +1 - (5x+1)}{h( \sqrt{5(x+h)+1} + \sqrt{5x+1} )} && \text{Multiply out numerator}\\ &=\dfrac{5h}{h( \sqrt{5(x+h)+1} + \sqrt{5x+1} )} && \text{Simplify}\\ &=\dfrac{5}{ \sqrt{5(x+h)+1} + \sqrt{5x+1} }&& \text{Cancel} \end{align*}
Other formulas used for the difference quotient are: \dfrac{f(x)-f(a)}{x-a} and \dfrac{f(a+h)−f(a)}{h}