2.2e: Exercises - Attributes of Functions

Last updated
Save as PDF

Page ID: 38322

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A: Concepts

Exercise $\PageIndex{A}$

1) Why does the domain differ for different functions?
2) How do we determine the domain of a function defined by an equation?
3) Explain why the domain of $f(x)=\sqrt[3]{x}$ is different from the domain of $f(x)=\sqrt{x}$.
4) When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?
5) How do you graph a piecewise function?

Answers to Odd Exercises:

1. The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.

3. There is no restriction on x for $f(x)=\sqrt[3]{x}$ because you can take the cube root of any real number. So the domain is all real numbers, $(−∞,∞)$. When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x-values are restricted for $f(x)=\sqrt{x}$ to nonnegative numbers and the domain is $[0,∞)$.

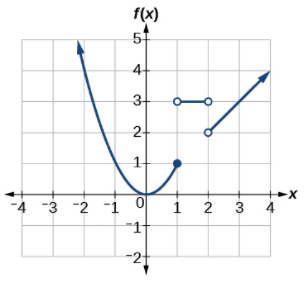
5. Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x-axis and y-axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate $−∞$ or $∞$. Combine the graphs to find the graph of the piecewise function.

B: Find the Domain given an Equation

Exercise $\PageIndex{B}$

$ \bigstar $ Find the domain of each function. State the domain in interval notation.

7) $f(x)=5−2x^2 \\[3pt]$

8) $f(x)=−2x(x−1)(x−2) \\[3pt]$

9) $f(x)=3\sqrt{x-2} \\[3pt]$

10) $f(x)=3-\sqrt{6-2x} \\[3pt]$

11) $f(x)=\sqrt{4-3x} \\[3pt]$

12) $f(x)=\sqrt{x^2+4} \\[3pt]$

13. $ f(x)=\sqrt{12-3x}+\sqrt{x-1} \\[3pt]$

14. $f(x)=\sqrt[3]{1-2x} \\[3pt]$

15) $f(x)=\sqrt[3]{x-1} \\[3pt] $

16) $f(x)=\dfrac{9}{x-6} $

17) $f(x)=\dfrac{1}{x^2-x-6} \\[5pt]$

18) $f(x)=\dfrac{x}{x} \\[5pt]$

19) $f(x)=\dfrac{3x+1}{4x+2} \\[5pt]$

20) $f(x)=\dfrac{x-3}{x^2+9x-22} \\[5pt]$

21) $f(x)=\dfrac{x^2-9x}{x^2-81} \\[5pt]$

22) $f(x)=\dfrac{2x^3−250}{x^2−2x−15} \\[6pt]$

23) $f(x)=\dfrac{\sqrt{x+4}}{x-4} \\[6pt]$

24) $ f(x)=\dfrac{x}{x-5}+\dfrac{\sqrt{x-3}}{2x-7}$

25) $ f(x)=\dfrac{5}{\sqrt{x-3}} \\[6pt]$

26) $ f(x)=\dfrac{2x+1}{\sqrt{5-x}} \\[6pt]$

27) $ f(x)=\dfrac{\sqrt{x-6}}{\sqrt{x-4}} \\[6pt] $

28) $ f(x)=\dfrac{\sqrt{x-4}}{\sqrt{6-x}} $

30) $f(x)= \sqrt{x^2-6x+8} \\[3pt]$

30.1) $f(x)= \sqrt{x^2(x-1)(x+3)} \\[3pt]$

30.2) $f(x)= \sqrt{\dfrac{(x-1)}{(x+2)(x+5)^2}} \\[3pt]$

30.3) $f(x)= \sqrt{\dfrac{(x-1)^2}{(x-2)^2(x+7)}} \\[3pt]$

Answers to Odd Exercises:

7. $(-\infty,\infty)$

9. $ [2,\infty)$

11. $ \left(-\infty,\dfrac{4}{3} \right] $

13. $ [1,4] $

15. $(-\infty,\infty)$

17. $(-\infty,-2)\cup(-2,3)\cup(3,\infty)$

19. $\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )$

21. $(-\infty,-9)\cup(-9,9)\cup(9,\infty)$

23. $ [-4,4)\cup(4,\infty)$

25. $ (3,\infty) $

27. $\left[6,\infty\right)$

C: Find the Domain, Range, and Intercepts given a Continuous Graph

Exercise $\PageIndex{C}$

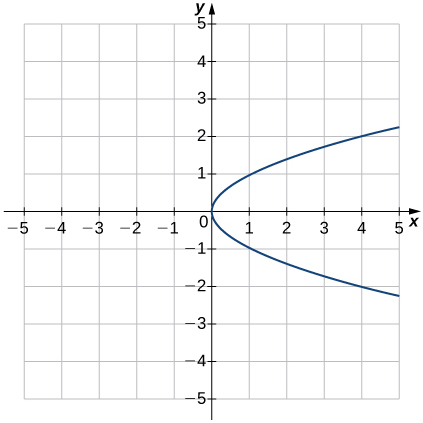
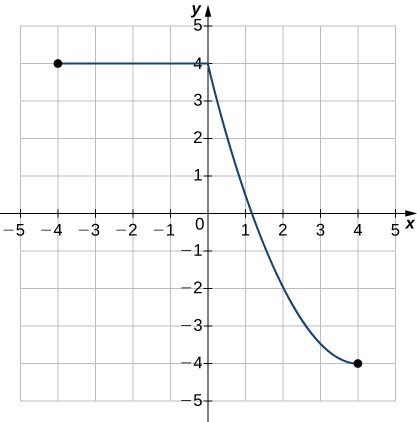
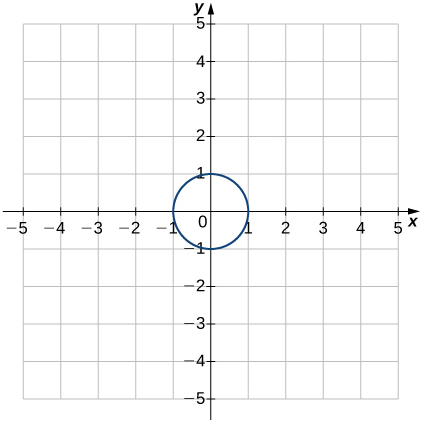
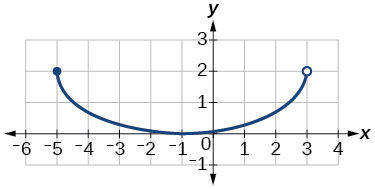
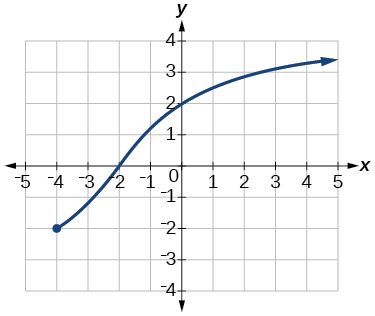
$ \bigstar $ For each function whose graph is illustrated below, (a) Determine the domain and range and state results in interval notation, and (b) State the $x$- and $y$-intercepts.

31)

$Graph of a function from $\left(2, 8\right]$.$

32)

$Graph of a function from $\left[4, 8\right)$.$

33)

$Graph of a function [-4,4]$

35)

$Graph of a function [-5,3)$

36)

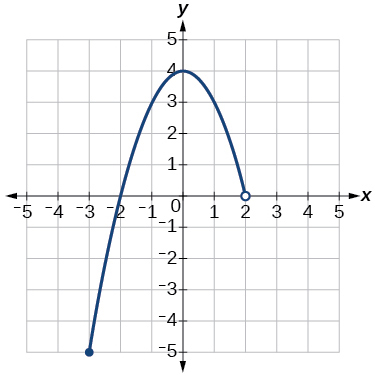$Graph of a function from [-3, 2).$

37)

$Graph of a function from (-infinity, 2].$

38)

$Graph of a function from [-4, infinity).$

39)

$Graph of a function from [-6, -1/6]U[1/6, 6]/.$

40)

$2.2e #40.png$

41)

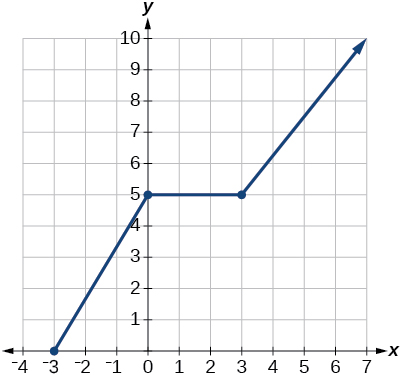$Graph of a function from [-3, infinity).$

Answers to Odd Exercises:

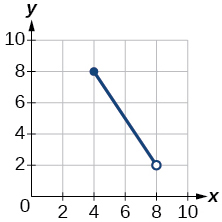
31. (a) domain: $(2,8]$; range: $[6,8) $;
(b) no intercepts

33. (a) domain: $ [-4,4] $; range: $ [0,2] $;
(b) intercepts: $(-4,0)$, $(4,0)$, $(0,2)$

35. (a) domain: $[−5,3)$; range: $[0,2]$;
(b) intercepts: $(-1,0)$, $(0, \approx .1)$

37. (a) domain: $\left(−\infty,1\right]$, range: $\left[0,\infty\right)$;
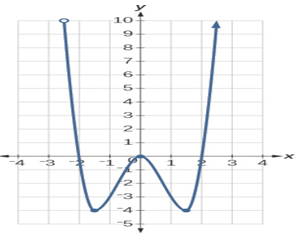
(b) intercepts: $ (1,0) $, $ (0,1.5) $

39. (a) domain: $[−6,−\frac{1}{6}]\cup[\frac{1}{6},6]$;
range: $[−6,−\frac{1}{6}]\cup[\frac{1}{6},6]$;
(b) no intercepts

41. (a) domain: $\left[−3, \infty\right)$; range: $\left[0,\infty\right)$;
(b) intercepts: $ (-3,0) $, $ (0,5) $

D: Find Domain and Range given a Piecewise Graph

Exercise $\PageIndex{D}$

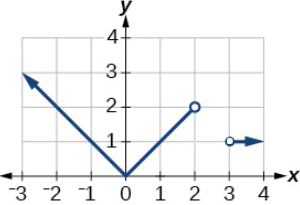
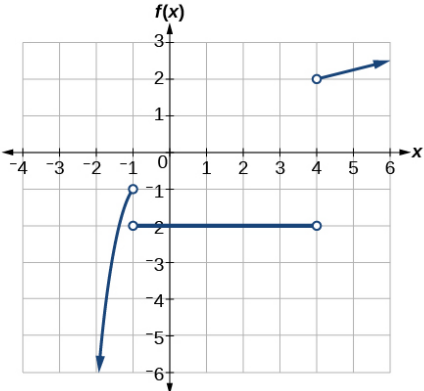
$ \bigstar $ Find the domain and range of the following graphs.

48. (a)

$2.2e piecewise #10 from 2.4.e.png$

(b)

$2.2e piecewise #6 from 2.4.e.png$

49. (a)

$2.2e piecewise #1 from 2.4.4s.png$

(b)

$2.2e piecewise #2 from 2.4.4s.png$

50. (a)

$2.2e piecewise #8 from 2.4.e.png$

(b)

$2.2e piecewise #12 from 2.4.e.png$

51. (a)

$2.2e piecewise #9 from 2.4.e.png$

(b)

$2.2e piecewise #5 from 2.4.e.png$

52.

$2.2e piecewise #14 from 2.4.e.png$

53.

$2.2e piecewise #15 from 2.4.e.png$

54.

$2.2e piecewise #16 from 2.4.e.png$

55.

$2.2e piecewise #17 from 2.4.e.png$

56.

$2.2e piecewise #3 from 2.4.6s.png$

57.

$2.2e piecewise #11 from 2.4.e.png$

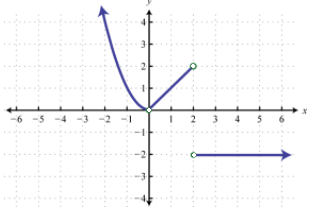
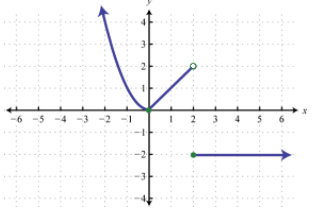
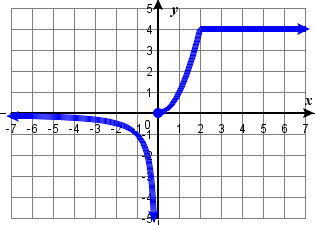
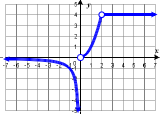
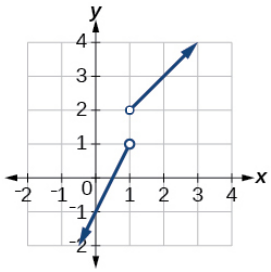
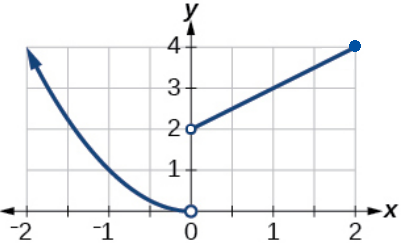
Answers to Odd Exercises:: 49. (a) domain: $ ( -\infty, \infty) $, range: $ [0, \infty ) $ (b) domain: $ ( -\infty, 2) \cup (2,\infty) $, range: $ [0, \infty ) $
51. (a) domain: $ ( -\infty, -4) \cup (-4, \infty ) $, range: $ [-2, \infty) $ (b) domain: $ ( -\infty, -2 ) \cup (-2, \infty ) $, range: $ [-2, \infty) $
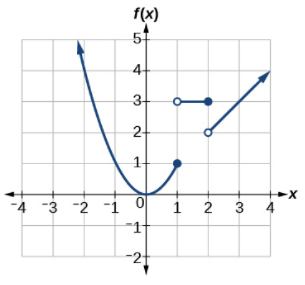
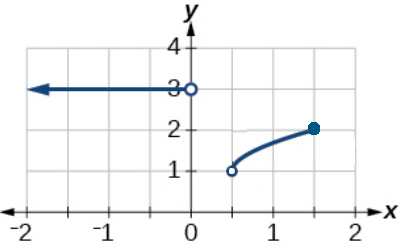
53. domain: $ ( -\infty, 0) \cup (1/2, 3/2] $, range: $ (1,2] \cup [3, 3] $ 55. domain: $ ( -\infty, 2) \cup (3, \infty) $, range: $ [0, \infty) $
57. domain: $ ( -\infty, -2) \cup (-2,0) \cup (0,2) \cup (2, \infty ) $, range: $ ( 0, \infty) $

E: Find Zeros and Intercepts given a Function

Exercise $\PageIndex{E}$: Find Zeros and Intercepts for a Function

$ \bigstar $ Find the zeros and intercepts of each function below.

63) $f ( x ) = 9 x ^ { 2 } - 12 x + 4$

64) $p ( x ) = 64 x ^ { 2 } - 1$

65) $f ( x ) = ( x + 5 ) ^ { 2 } + 1$

66) $f ( x ) = ( 3 x - 4 ) ^ { 2 } + 7$

67) $g ( x ) = - ( x + 1 ) ^ { 4 } + 16$

68) $f ( x ) = ( 2x -3 ) ^ { 2 } - 4$

68.1) $f ( x ) = \frac { 1 } { 3 } x ^ { 3 } + \frac { 1 } { 2 } x ^ { 2 } + \frac { 4 } { 3 } x + 2$

69.1) $ f(x) = 3x^3 - 2x^2 +27x -18 $

69.2) $f ( x ) = \dfrac { 4 x ^ { 2 } - 9 } { 2 x - 3 }$

70) $f ( x ) = \dfrac { 3 x ^ { 2 } - 2 x - 1 } { x ^ { 2 } - 1 }$

71) $f ( x ) = \dfrac { 1 } { x } - 3$

72) $f(x)=\dfrac{x}{x^2−16}$

73) $f ( x ) = \dfrac { 1 } { x + 5 }$

74) $h(x)=\dfrac{3}{x^2+4}$

75) $f ( x ) = \sqrt { 2 x - 3 } - 1$

76) $f ( x ) = 3 \sqrt { x - 7 } - 6$

77) $f ( x ) = 2 \sqrt { x + 2 } - 8$

78) $f(x)=−1+\sqrt{x+2}$

79) $f ( x ) = \sqrt [ 3 ] { x -8 } - 2$

80) $f ( x ) = 2 \sqrt [ 3 ] { x - 1 } + 6$

81) $g(x)=\sqrt{\dfrac{7}{x−5}}$

82) $f(x)=4|x^2+5|$

Answers to Odd Exercises:: 63). zeros: {2/3}; $x$-intercepts: (2/3,0); $y$-intercepts: (0,4) 65. {$-5 \pm i$}; no $x$ intercepts; (0, 26)
67). { $\pm 2$, $\pm 2i$ }; (2,0), (-2,0); (0,15) 69.1. zeros: $ \{ \pm 3i, \frac{2}{3} $; $x$-intercepts: (3/2,0); $y$-intercepts: (0,-18)
69.2). {-3/2}; (-3/2,0); (0,3) 71). {1/3}; (1/3, 0); no $y$-intercepts 73). no zeros; no $x$-intercepts; (0, $\frac{1}{5}$ )
75). {2}; (2,0); no $y$-intercept 77). {14}; (14,0); (0, $2\sqrt{2}-8$ )
79). {16}; (16,0); (0, -4) 81). no zeros; no $x$-intercepts; no $y$-intercept.

F: Find Zeros, Intercepts, and Symmetry given an Equation

Exercise $\PageIndex{F}$: Find Zeros, Intercepts and Symmetry for a graph given its equation

$ \bigstar $ For each equation below (a) Find the zeros and $x$- and $y$-intercept(s) of the graph, if any exist and (b) Test for symmetry.

$ y = x^{2} + 1 $
$ y = x^2-2x-8 $
$ y = x^{3} - x $

$ y = \frac{x^3}{4} - 3x $
$ y = \sqrt{x - 2} $
$ y = 2 \sqrt{x+4} - 2$

$ 3x - y = 7 $
$ 3x-2y = 10 $
$ (x+2)^2+y^2 = 16 $

$ x^{2} - y^{2} = 1 $
$ 4y^2 - 9x^2 = 36 $
$ x^{3}y = -4 $

Answers to odd exercises.

83. (a) The graph has no $x$-intercepts, $y$-intercept: $ (0, 1) $, zeros: $ \{ \pm i \} $.
(b) $x$-axis symmetry: no. $y$-axis symmetry: yes. Origin symmetry: no.

85. $x$-intercepts: $ (-1, 0), (0, 0), (1, 0) $, $y$-intercept: $ (0, 0) $, zeros: $ \{ -1,\; 0,\; 1\} $.
(b) $x$-axis symmetry: no. $y$-axis symmetry: no. Origin symmetry: yes.

87. $x$-intercept: $ (2, 0) $, The graph has no $y$-intercepts, zeros: $ \{ 2 \} $.
(b) $x$-axis symmetry: no. $y$-axis symmetry: no. Origin symmetry: no.

89. $x$-intercept: $ (\frac{7}{3}, 0) $, $y$-intercept: $ (0, -7) $, zeros: $ \{ \frac{7}{3} \} $.
(b) $x$-axis symmetry: no. $y$-axis symmetry: no. Origin symmetry: no.

91. $x$-intercepts: $ (-6, 0) $, $ (2,0) $, $y$-intercepts: $ \left(0, \pm 2\sqrt{3}\right) $, zeros: $ \{ 2, -6 \} $.
(b) $x$-axis symmetry: yes. $y$-axis symmetry: no. Origin symmetry: no.

93. The graph has no $x$-intercepts, $y$-intercepts: $ (0, \pm 3) $, zeros: $ \{ \pm 2i \} $.
(b) $x$-axis symmetry: yes. $y$-axis symmetry: yes. Origin symmetry: yes.

G: Find Symmetry for an Equation or a Function

Exercise $\PageIndex{G}$

$ \bigstar $ Determine the symmetry for the following equations

$ y = 2x + 5 $
$ y = x^2+3 $
$ x = y^2 -6 x $
$7x + 3y^3 =5$

$ y = | x | - 2 \\[4pt] $
$ x = | y | +3 \\[4pt] $
$ (x+1)^2 = |y - 2xy| $

$ x^2y^2 +3xy=1 $
$ y = \dfrac{3x}{x^2+9} \\[6pt]$
$ x = \dfrac {y^2-4}{2y} \\[6pt] $

Answers to Odd Exercises:: 97) no symmetry 99) x-axis symmetry 101) y-axis symmetry 103) x-axis symmetry 105) origin symmetry

$ \bigstar $ Given the following functions (a) Determine the symmetry of the function and (b) State if the function is even or odd.

$f(x)=(x−2)^2 \\[4pt] $
$f(x)=3x^4 \\[4pt] $
$h(x)=2x−x^3$

$g(x)=\sqrt{x} \\[4pt] $
$ f(x) = x \sqrt{1-x^2} \\[4pt] $
$ f(x) = x^2 \sqrt{x^2+16} $

$ f(x) = \sqrt{x^3+2x} \\[4pt] $
$ f(x)=\sqrt[3]{2x^2+1} \\[4pt] $
$ f(x) = \sqrt[3]{x} $

117. $h(x)=\dfrac{1}{x}+3x \\[2pt] $
118. $ f(x) = \dfrac{x}{| 3x |} \\[2pt] $
118.1 $ f(x) = | x^3+2x | $

Answers to Odd Exercises:: 109) (a) y-axis symmetry, (b) even function 111) (a) neither y-axis or origin symmetry, (b) neither even nor odd
113) (a) y-axis symmetry, (b) even function 115) (a) y-axis symmetry, (b) even function 117) (a) origin symmetry, (b) odd function,

H: Attributes from Graphs

Exercise $\PageIndex{H}$

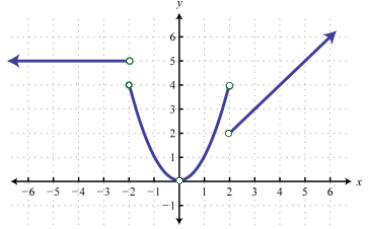
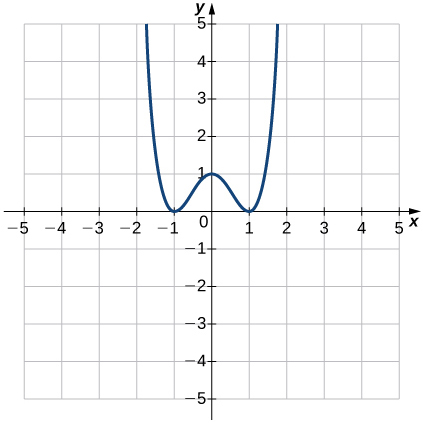
$ \bigstar $ Determine the following for each graph below. These graphs do not have arrows, but assume that a graph continues at both ends if it extends beyond the given grid.

Domain and range
$x$ -intercept, if any (estimate where necessary)
$y$-Intercept, if any (estimate where necessary)
The intervals for which the function is increasing (only if a function)
The intervals for which the function is decreasing (only if a function)
The intervals for which the function is constant (only if a function)
Symmetry about any axis and/or the origin
Whether the function is even, odd, or neither (only if a function)

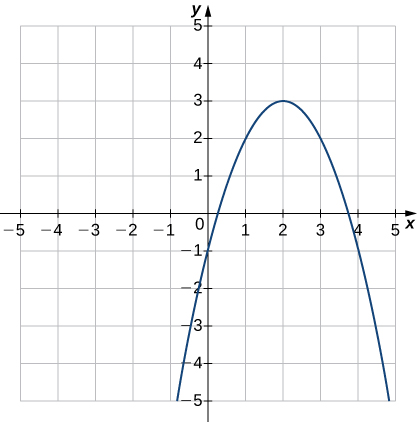
121)

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is curved. The relation decreases until it hits the point (-1, 0), then increases until it hits the point (0, 1), then decreases until it hits the point (1, 0), then increases again.$

122)

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is a parabola. The curved relation increases until it hits the point (2, 3), then begins to decrease. The approximate x intercepts are at (0.3, 0) and (3.7, 0) and the y intercept is is (-1, 0).$

123)

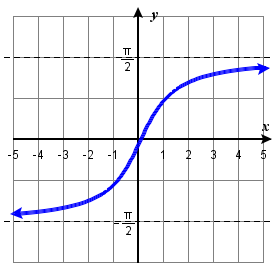
$2.23 #123.png - An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is curved. The curved relation increases the entire time. The x intercept and y intercept are both at the origin.$

124)

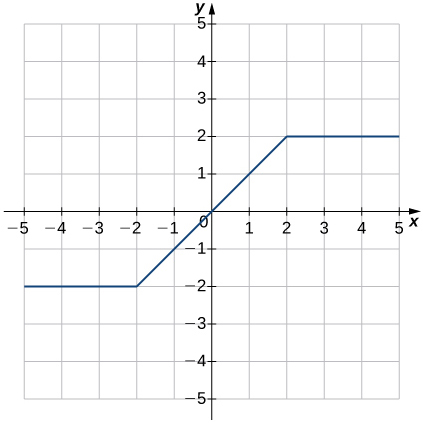
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is a horizontal line until the point (-2, -2), then it begins increasing in a straight line until the point (2, 2). After these points, the relation becomes a horizontal line again. The x intercept and y intercept are both at the origin.$

125)

$2.2e #125.png An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is a horizontal line until the origin, then it begins increasing in a straight line. The x intercept and y intercept are both at the origin and there are no points below the x axis.$

126)

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is a sideways parabola, opening up to the right. The x intercept and y intercept are both at the origin and the relation has no points to the left of the y axis. The relation includes the points (1, -1) and (1, 1)$

127)

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that starts at the point (-4, 4) and is a horizontal line until the point (0, 4), then it begins decreasing in a curved line until it hits the point (4, -4), where the graph ends. The x intercept is approximately at the point (1.2, 0) and y intercept is at the point (0, 4).$

128)

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a relation that is circle, with x intercepts at (-1, 0) and (1, 0) and y intercepts at (0, 1) and (0, -1).$

Answers to Odd Exercises:

121) Solution: Function; a. Domain: $ ( -\infty, \infty) $, range: $ [0, \infty ) $ b. $ (-1, 0)$, $ (1, 0)$ c. $ (0,1) $ d. $−1<x<0$ and $ x > 1 $ e. $ x<−1$ and $0<x<1$ f. Not constant g. $y$-axis h. Even

123) Solution: Function; a. Domain: $ ( -\infty, \infty) $, range: $ (−\frac{\pi}{2}, \frac{\pi}{2}) $ b. $ (0, 0) $ c. $ (0, 0) $ d. all real numbers e. None f. Not constant g. Origin h. Odd

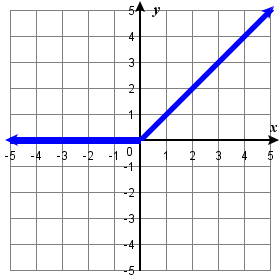
125) Solution: Function; a. Domain: $ ( -\infty, \infty) $, range: $ [0, \infty ) $ b. $ \{ (x,0) | \; x ≤ 0 \} $ c. $ (0, 0) $ d. $x>0$ e. Not decreasing f. $x<0$ g. No Symmetry h. Neither

127) Solution: Function; a. Domain: $ [-4, 4 ] $, range: $ [-4, 4 ] $ b. $ ( \approx 1.2, 0) $ c. $ (0, 4) $ d. Not increasing e. $0<x<4$ f. $−4<x<0$ g. No Symmetry h. Neither

I: Extrema and Continuity given a Graph

Exercise $\PageIndex{I}$

$ \bigstar $ Find the following attributes in the graphs below.
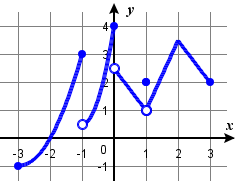
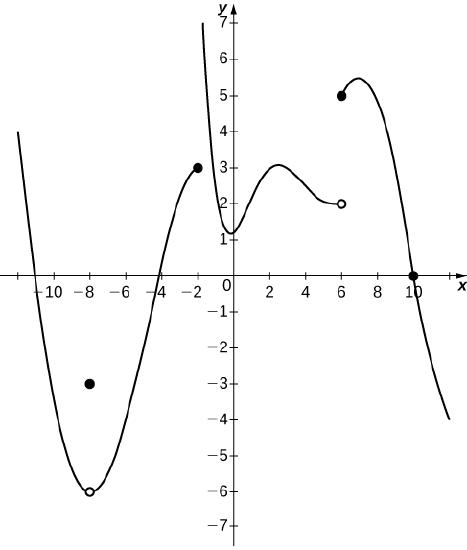
Assume that graphs do NOT extend beyond the given grid unless arrows are drawn. For minima and maxima, state the coordinates of the point or the label on the point as appropriate. Estimate if needed.

a) Local minima b) Absolute minima c) Local maxima d) Absolute maxima
e) Places where the function is discontinuous

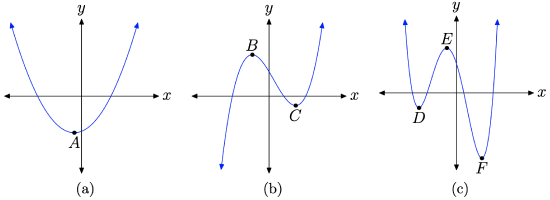
131)			132)
$clipboard_e7efd93ac6a58fabb7d145dd66629df0d.png$			$CNX_PreCalc_Figure_03_04_215.jpg$

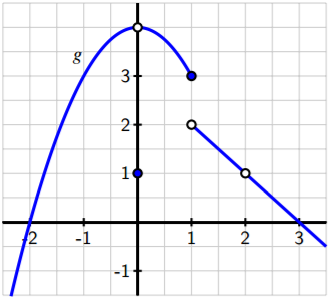
Assume that graphs do NOT extend beyond the given grid unless arrows are drawn. Estimate if needed.

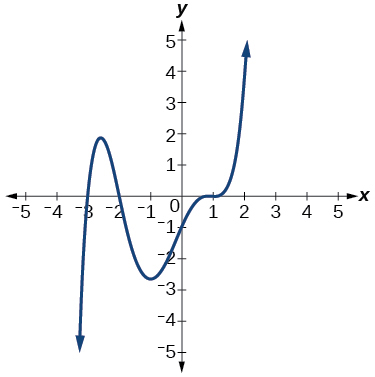
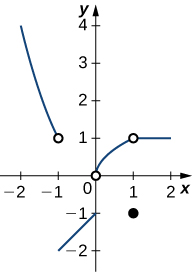
133)	134)	135)	136)
$A graph of a piecewise function with several segments. The first is a decreasing concave up curve existing for x < -1. It ends at an open circle at (-1, 1). The second is an increasing linear function starting at (-1, -2) and ending at (0,-1). The third is an increasing concave down curve existing from an open circle at (0,0) to an open circle at (1,1). The fourth is a closed circle at (1,-1). The fifth is a line with no slope existing for x > 1, starting at the open circle at (1,1).$	$2.2e #134 piecewise graph v2.png$	$A graph of a piecewise function with three segments and a point. The first segment is a curve opening upward with vertex at (-8, -6). This vertex is an open circle, and there is a closed circle instead at (-8, -3). The segment ends at (-2,3), where there is a closed circle. The second segment stretches up asymptotically to infinity along x=-2, changes direction to increasing at about (0,1.25), increases until about (2.25, 3), and decreases until (6,2), where there is an open circle. The last segment starts at (6,5), increases slightly, and then decreases into quadrant four, crossing the x axis at (10,0). All of the changes in direction are smooth curves.$	$clipboard_e18fa5c96d2058cf72aa67def61f9269c.png$

Answers to Odd Exercises:: 131a) (a) A, (b) A, (c) none, (d) none (e) none; 131b) (a) C, (b) none, (c) B, (d) none, (e) none
131c) (a) D,F, (b) F, (c) E, (d) none, (e) none
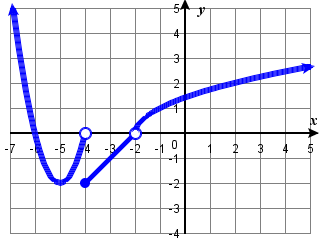
133) (a) (1,-1), (b) (-1,-2); (c) none, (d) (-2,4); (e) x=-1, x=0, x=1
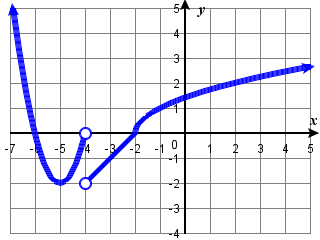
135) (a) (0, 1.2), (b) none; (c) (-8, -3), (2,3), (7, 5.5) (d) (-2,7) (e) x=-8, x=-2, x=6.