2.5e: Exercises Inverse Functions

Last updated
Save as PDF

Page ID: 45445

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

A: Concepts

Exercise $\PageIndex{A}$

1) Describe why the horizontal line test is an effective way to determine whether a function is one-to-one?

2) Why do we restrict the domain of the function $f(x)=x^2$ to find the function’s inverse?

3) Can a function be its own inverse? Explain.

4) Are one-to-one functions either always increasing or always decreasing? Why or why not?

5) How do you find the inverse of a function algebraically?

Answers to Odd Exercises:

1. Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that $y$-values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no $y$-values repeat and the function is one-to-one.

3. Yes. For example, $f(x)=\dfrac{1}{x}$ is its own inverse.

5. Given a function $y=f(x)$, solve for $x$ in terms of $y$. Interchange the $x$ and $y$. Solve the new equation for $y$. The expression for $y$ is the inverse, $y=f^{-1}(x)$.

B: Horizontal Line Test

Exercise $\PageIndex{B}$)

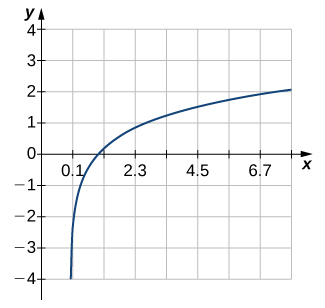
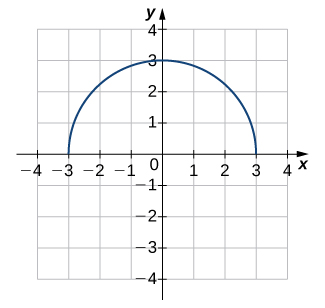
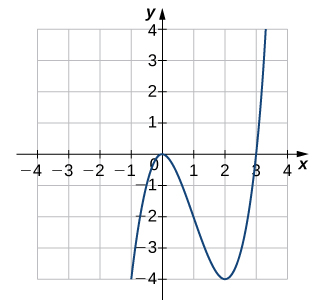
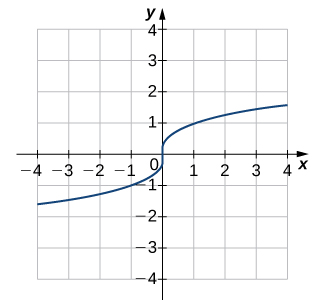
$ \bigstar $ For the following exercises, use the horizontal line test to determine whether each of the given graphs is one-to-one.

$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a function that decreases in a straight in until the origin, where it begins to increase in a straight line. The x intercept and y intercept are both at the origin.$

$An image of a graph. The x axis runs from 0 to 7 and the y axis runs from -4 to 4. The graph is of a function that is always increasing. There is an approximate x intercept at the point (1, 0) and no y intercept shown.$

$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a function that resembles a semi-circle, the top half of a circle. The function starts at the point (-3, 0) and increases until the point (0, 3), where it begins decreasing until it ends at the point (3, 0). The x intercepts are at (-3, 0) and (3, 0). The y intercept is at (0, 3).$

10.

$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved function. The function increases until it hits the origin, then decreases until it hits the point (2, -4), where it begins to increase again. There are x intercepts at the origin and the point (3, 0). The y intercept is at the origin.$

11.

$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved function that is always increasing. The x intercept and y intercept are both at the origin.$

12.

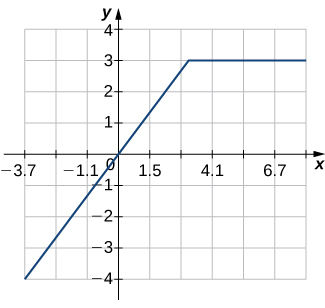$An image of a graph. The x axis runs from -4 to 7 and the y axis runs from -4 to 4. The graph is of a function that increases in a straight line until the approximate point (, 3). After this point, the function becomes a horizontal straight line. The x intercept and y intercept are both at the origin.$

13.

$Graph of a circle.$

14.

$Graph of a parabola.$

15.

$Graph of a rotated cubic function.$

16.

$Graph of half of 1/x.$

17.

$Graph of a function$

18.

$Graph of a parabola.$

Answers to Odd Exercises:: 7. Not one-to-one, $\;$ 9. Not one-to-one, $\;$ 11. One-to-one, $\;$ 13. Not one-to-one, $\;$ 15. One-to-one, $\;$ 17. Not one-to-one

C: Graphs of Inverse Functions

Exercise $\PageIndex{C}$

$ \bigstar $ For the following exercises, use the graph of $f$ to sketch the graph of its inverse function.

19)
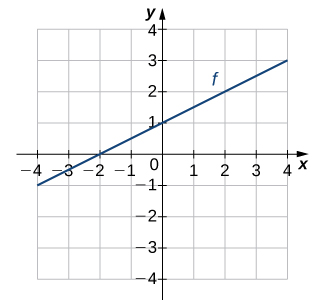$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of an increasing straight line function labeled “f” that is always increasing. The x intercept is at (-2, 0) and y intercept are both at (0, 1).$

20)
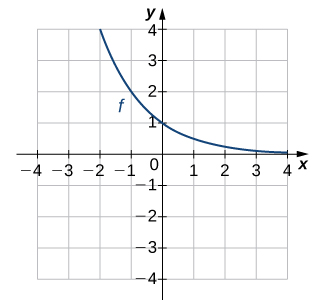$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved decreasing function labeled “f”. As the function decreases, it gets approaches the x axis but never touches it. The function does not have an x intercept and the y intercept is (0, 1).$

21)
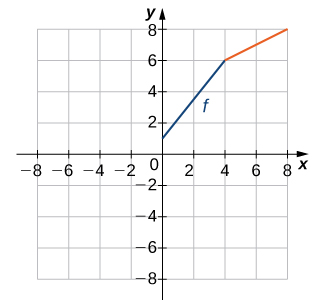$An image of a graph. The x axis runs from -8 to 8 and the y axis runs from -8 to 8. The graph is of an increasing straight line function labeled “f”. The function starts at the point (0, 1) and increases in straight line until the point (4, 6). After this point, the function continues to increase, but at a slower rate than before, as it approaches the point (8, 8). The function does not have an x intercept and the y intercept is (0, 1).$

22)
$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a decreasing curved function labeled “f”, which ends at the origin, which is both the x intercept and y intercept. Another point on the function is (-4, 2).$

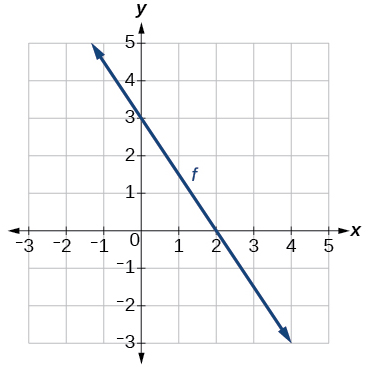
$ \bigstar $ Use the graph of the one-to-one function shown in the Figure to answer the following questions.

23) Find $f(0) \\[4pt] $.

24) Solve $f(x)=0 \\[4pt] $.

25) Find $f^{-1}(0) \\[4pt] $.

26) Solve $f^{-1}(x)=0$.

$Graph of a line.$

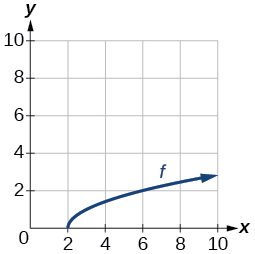
27) Sketch the graph of $f^{-1} \\[4pt] $.

28) Find $f(6)$ and $f^{-1}(2) \\[4pt] $.

29) If the complete graph of $f$ is shown, find the domain of $f \\[4pt] $.

30) If the complete graph of $f$ is shown, find the range of $f$

$Graph of a square root function.$

Answers to Odd Exercises:

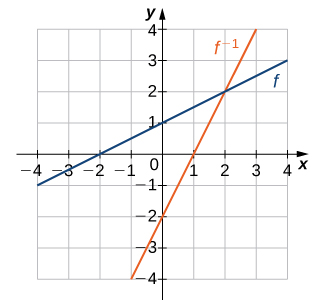
19) $An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of two functions. The first function is an increasing straight line function labeled “f”. The x intercept is at (-2, 0) and y intercept are both at (0, 1). The second function is of an increasing straight line function labeled “f inverse”. The x intercept is at the point (1, 0) and the y intercept is at the point (0, -2).$

21)
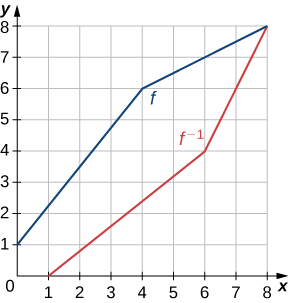
$\;$ $CNX_Calc_Figure_01_04_212.jpeg$

23. $3$

25. $2$

29. $[2, \infty ) $

27.

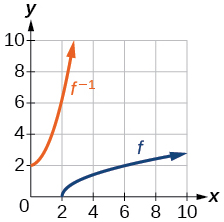
$Graph of a square root function and its inverse.$

D: Inverse Function Values

Exercise $\PageIndex{D}$

$ \bigstar $ Find values of a function from its inverse and vice versa.

31) If $f(6)=7$, find $f^{-1}(7)$.

32) If $f(3)=2$, find $f^{-1}(2)$.

32.1) If $f(4)=5$, find $f^{-1}(4)$.

32.2) If $f^{-1}(9)=3$, find $f(9)$.

33) If $f^{-1}(−4)=−8$, find $f(−8)$.

34) If $f^{-1}(−2)$=−1, find $f(−1)$.

$ \bigstar $ Given the table of values for $f$, determine the following.

$ \begin{array}{ll}
35) \text{ Find } f(1). \qquad \qquad &
36) \text{ Solve} f(x)=3. \\
37) \text{ Find } f^{-1}(4).&
38) \text{ Solve } f^{-1}(x)=7. \\
39) \text{ Solve } f^{-1}(x)=11. &
40) \text{ Find } f^{-1}(12).
\end{array} $

$x$	1	4	7	12	16
$f(x)$	12	11	9	4	3

Answers to Odd Exercises:: 31. $6$ $\qquad$ 33. $-4$, $\qquad$ 35. $12$, $\qquad$ 37. $12$, $\qquad$ 39. Undefined

E: Verify Two Functions are Inverses

Exercise $\PageIndex{E}$

$ \bigstar $ For the following exercises, use composition to determine which pairs of functions are inverses.

41) $f(x)=8x, \; g(x)=\dfrac{x}{8}$

42) $f(x)=\dfrac{2}{3}x+2, \; g(x)=\dfrac{3}{2}x+3$

43) $f(x)=5x−7, \; g(x)=\dfrac{x+5}{7}$

44) $f(x)=8x+3, \; g(x)=\dfrac{x-3}{8}$

45) $f(x)=\dfrac{1}{x−1}, x≠1, \; g(x)=\dfrac{1}{x}+1,x≠0 $

46) $f(x)=−3x+5$, $g(x)=\dfrac{x-5}{-3}$

47) $f(x)=\dfrac{x}{2+x}$, $g(x)=\dfrac{2x}{1-x} \\[2pt] $

48) $f(x)=x^3+1, \; g(x)=(x−1)^{1/3} \\[2pt] $

49) $f(x)=x^2+2x+1,x≥−1, \; g(x)=−1+\sqrt{x},x≥0 \\[2pt] $

50) $f(x)=\sqrt{4−x^2},0≤x≤2, \; g(x)=\sqrt{4−x^2},0≤x≤2 \\[2pt] $

Answers to Odd Exercises:: 41) inverses. 43) not inverses. 45) inverses. 47) inverses 49) inverses

F: Find inverses of linear and rational functions

Exercise $\PageIndex{F}$

$ \bigstar $ Find the formula for the inverse function $f^{−1}(x)$.

51) $f(x)=x+3 \\[2pt] $

52) $f(x)=x+5 \\[2pt] $

53) $f(x)=2−x \\[2pt] $

54) $f(x)=3−x \\[2pt] $

55) $f(x) = 7x−9 \\[2pt] $

56) $f(x) = 6x−4 \\[2pt] $

57) $f(x) = −5x+2 \\[2pt] $

58) $f(x) = 6x+8$

59) $f(x)=\dfrac{3}{x+2} \\[3pt] $

60) $f(x)=\dfrac{x}{x-2} \\[3pt] $

61) $f(x)= \dfrac{x-4}{x+2} \\[3pt] $

62) $f(x)= \dfrac{2x-7}{x+6} \\[3pt] $

63) $f(x)= \dfrac{2x+3}{5x+4} \\[3pt] $

64) $f(x)= \dfrac{2x+6}{x-3} \\[3pt] $

65) $f(x) = \dfrac{9x−3}{9x+7} $

66) $f(x) = \dfrac{3x+7}{2x+8} \\[3pt] $

67) $f(x) = \dfrac{4x+2}{4x+3} \\[3pt] $

68) $f(x) = \dfrac{8x−7}{3x−6} \\[3pt] $

69) $f(x) = \dfrac{4x−1}{2x+2} \\[3pt] $

70) $f(x)=−\dfrac{9x−3}{7x+6}$

Answers to Odd Exercises:: 51. $f^{-1}(x)=x−3 $ 53. $f^{-1}(x)=2−x$
55. $f^{-1}(x)=\frac{x+9}{7}$ 57. $f^{-1}(x)=−\frac{x−2}{5}$ 59. $f^{-1}(x) = \frac{3}{x} - 2 $ 61. $f^{-1}(x) = -2\frac{x+2}{x-1} $
63. $f^{-1}(x) = \frac{-4x+3}{5x-2} $ 65. $f^{-1}(x)=−\frac{7x+3}{9x−9}$ 67. $f^{-1}(x)=−\frac{3x−2}{4x−4}$ 69. $f^{-1}(x)=−\frac{2x+1}{2x−4}$

G: Find inverses of odd degree power and root functions

Exercise $\PageIndex{G}$

$ \bigstar $ Find the formula for the inverse function $f^{−1}(x)$.

71) $f(x)=x^3+1 \\[2pt] $

72) $f(x)=x^3−27 \\[2pt] $

73) $f(x)=(x-4)^3 \\[2pt] $

74) $y=(x+8)^3+3$

75) $f(x) = 5x^3−5 \\[2pt] $

76) $f(x) = 4x^5−9 \\[2pt] $

77) $f(x) = 3x^5−9 \\[2pt] $

78) $f(x) = 5x^7+4$

79) $f(x) = 9x^9+5 \\[2pt] $

80) $f(x) = 4x^7−3 \\[2pt] $

81) $f(x)=\sqrt[3]{x−4} \\[2pt] $

82) $f(x)=\sqrt[3]{3x+1}$

83) $f(x)=\sqrt[3]{x} + 5 \\[2pt] $

84) $f(x)=\sqrt[3]{x} - 8 \\[2pt] $

85) $f(x) = \sqrt[3]{−6x−4} \\[2pt] $

86) $f(x) = \sqrt[3]{9x−7}$

87) $f(x) = \sqrt[7]{−3x−5} \\[2pt] $

88) $f(x) = \sqrt[7]{8x−3} \\[2pt] $

89) $f(x) = \sqrt[3]{6x+7} \\[2pt] $

90) $f(x) = \sqrt[9]{8x+2}$

Answers to Odd Exercises:: 71. $f^{−1}(x)=\sqrt[3]{x-1} $ 73. $f^{−1}(x) = 4 + \sqrt[3]{x}$ 75. $\sqrt[3]{\frac{x+5}{5}}$ 77. $\sqrt[5]{\frac{x+9}{3}}$ 79. $\sqrt[9]{\frac{x−5}{9}} $
81. $f^{-1}(x) = x^3+4 $ 83. $f^{-1}(x) = (x-5)^3 $ 85. $−\frac{x^3+4}{6}$ 87. $−\frac{x^7+5}{3}$ 89. $\frac{x^3−7}{6}$

H: Find inverses of even degree power and root functions

Exercise $\PageIndex{H}$ ]

$ \bigstar $ Find $f^{-1}(x)$ for each function below. In #105-108 also state the restrictions for $x$ in $f^{-1}$.

91) $f(x) = x^4, \;$ $x \le 0 \\[2pt] $

92) $f(x) = x^4, \;$ $x \ge 0 \\[2pt] $

93) $f(x) = x^2−1, \;$ $x \le 0 \\[2pt] $

94) $f(x) = x^2+2, \;$ $x \ge 0 \\[2pt] $

95) $f(x)=x^2−4, \; x≥0 \\[2pt] $

96) $f(x)=x^2+11, \;x≤0$

97) $f(x) = x^4+3, \;$ $x \le 0 \\[2pt] $

98) $f(x) = x^4−5, \;$ $x \ge 0 \\[2pt] $

99) $f(x)=(x−1)^2, \; x≥1 \\[2pt] $

100) $f(x)=(x+3)^2, \; x≥-3 \\[2pt] $

101) $f(x) = (x−1)^2, \;$ $x \le 1 \\[2pt] $

102) $f(x) = (x+2)^2, \;$ $x \ge −2$

103) $f(x)=x^2-8x+3, \; x≤4 \\[2pt] $

104) $f(x)=x^2+2x+50, \; x≥-1 \\[2pt] $

105) $f(x)=\sqrt{x−1} \\[2pt] $

106) $f(x)=\sqrt{x+2} \\[2pt] $

107) $f(x)=\sqrt{x}+9 \\[2pt] $

108) $f(x)=\sqrt{x}-1$

Answers to Odd Exercises:

91. $f^{-1}(x) =−\sqrt[4]{x}$

93. $f^{-1}(x) =−\sqrt{x+1}$

95. $f^{-1}(x) = \sqrt{x+4} $

97. $f^{-1}(x) =−\sqrt[4]{x−3}$

99. $f^{-1}(x) = 1+ \sqrt{x} $

101. $f^{-1}(x) =−\sqrt{x}+1$

103. $f^{-1}(x) = 4-\sqrt{x+13} $

105. $f^{−1}(x)=x^2+1$, $x≥0$

107. $f^{-1}(x) = (x-9)^2,$ $x≥9$

I: Find the inverse and its domain and range

Exercise $\PageIndex{I}$

$ \bigstar $ Find a domain on which $f$ is one-to-one and non-decreasing. Then find the inverse of $f$.

111) $f(x)=(x+7)^2$

112) $f(x)=(x−6)^2$

113) $f(x)=x^2−5$

114) $ f(x)=3(x−4)^2+1$

Answers to Odd Exercises: 111. domain of $f(x)$: $\left[−7,\infty\right)$; $\quad$ $f^{-1}(x)=\sqrt{x}−7$ 113. domain of $f(x)$: $\left[0,\infty\right)$; $\quad$ $f^{-1}(x)=\sqrt{x+5}$

Search

Text Color

Text Size

Margin Size

Font Type