4.2e: Exercises - Graphs of Exponential Functions
- Page ID
- 45004
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A: Concepts
Example \(\PageIndex{A}\)
1) What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?
2) What is the advantage of knowing how to recognize transformations of the graph of a parent function algebraically?
3) Explore and discuss the graphs of \(F(x)=(b)^x\) and \(G(x)=\left ( \frac{1}{b} \right )^x\). Then make a conjecture about the relationship between the graphs of the functions \(b^x\) and \(\left ( \frac{1}{b} \right )^x\) for any real number \(b>0\).
4) Prove the conjecture made in the previous exercise.
5) Explore and discuss the graphs of \(f(x) = 4^x\), \(g(x)=4^{x-2}\), and \(h(x)=\left ( \frac{1}{16} \right )4^x\). Then make a conjecture about the relationship between the graphs of the functions \(b^x\) and \(\left ( \frac{1}{b^n} \right )b^x\) for any real number \(n\) and real number \(b>0\).
6) Prove the conjecture made in the previous exercise.
|
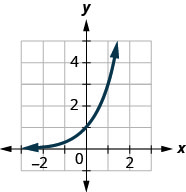
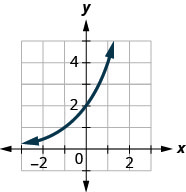
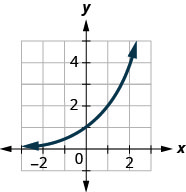
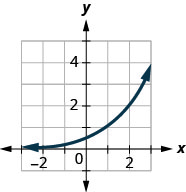
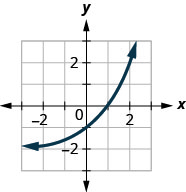
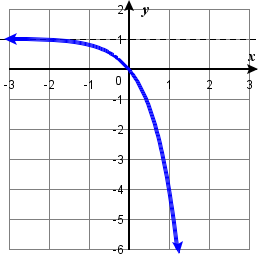
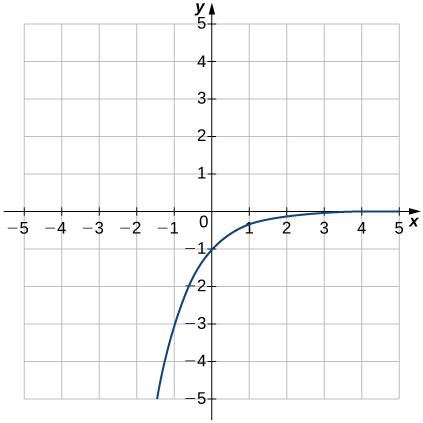
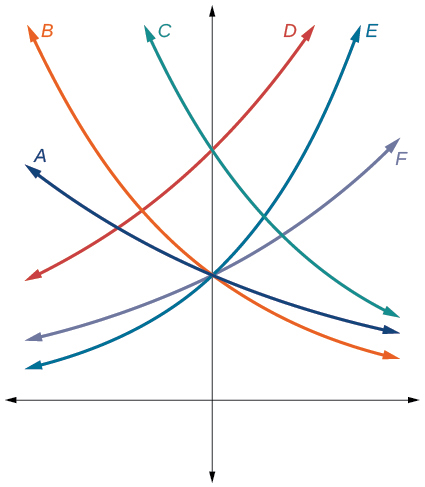
For the following exercises, match each function with one of the graphs in Figure at the right.
7) \(f(x)=2(0.69)^x \\[3pt] \) 8) \(f(x)=2(1.28)^x \\[3pt] \) 9) \(f(x)=2(0.81)^x \\[3pt] \) 10) \(f(x)=4(1.28)^x \\[3pt] \) 11) \(f(x)=2(1.59)^x \\[3pt] \) 12) \(f(x)=4(0.69)^x\) |
 |
|
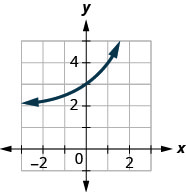
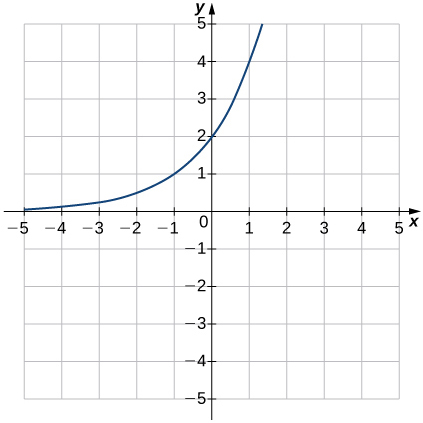
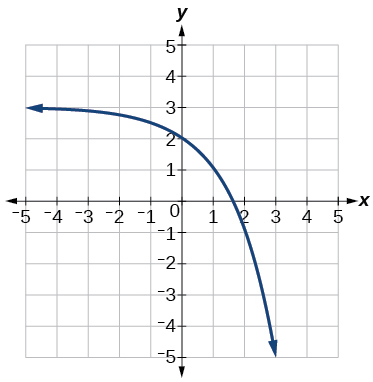
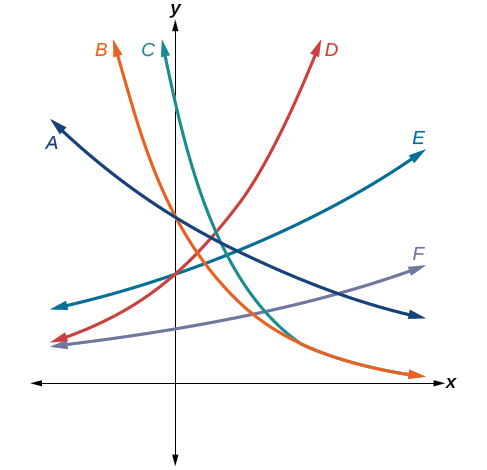
For the following exercises, use the graphs shown in Figure at the right. All have the form \(f(x)=ab^x\).
13) Which graph has the largest value for \(b? \\[3pt] \) 14) Which graph has the smallest value for \(b? \\[3pt] \) 15) Which graph has the largest value for \(a? \\[3pt] \) 16) Which graph has the smallest value for \(a\)?\ |
 |
- Answers to odd exercises:
-
1. An asymptote is a line that the graph of a function approaches, as \(x\) either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.
3. The graph of \(G(x)=\left ( \frac{1}{b} \right )^x\) is the refelction about the \(y\)-axis of the graph of \(F(x)=(b)^x\); For any real number \(b>0\) and function \(f(x)=(b)^x\) , the graph of \(\left ( \frac{1}{b} \right )^x\) is the the reflection about the \(y\)-axis, \(F(-x)\).
5. \(g(x)\) and \(h(x)\) are the same graph and are a horizontal shift to the right of the graph of \(f(x)\); For any real number \(n\), real number \(b>0\), and function \(f(x)=b^x\), the graph of \(\left ( \frac{1}{b^n} \right )b^x\) is the horizontal shift \(f(x-n)\).
7. B, 9. A, 11. E, 13. D, 15. C
B: Match Graphs With Equations
Exercise \(\PageIndex{B}\)
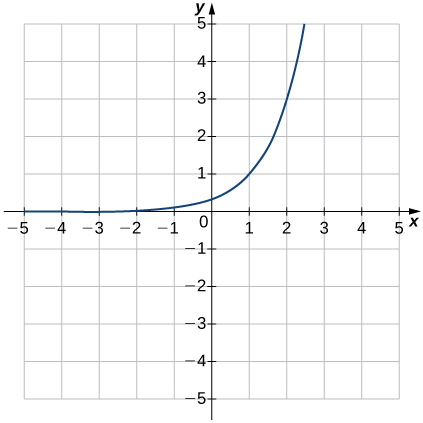
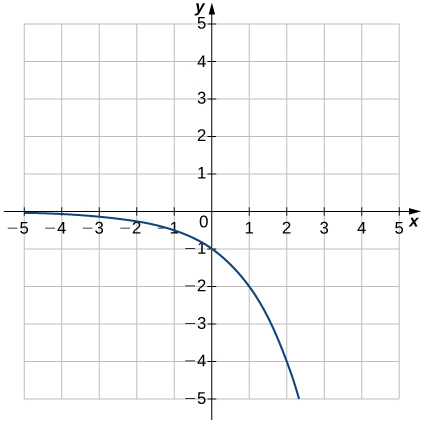
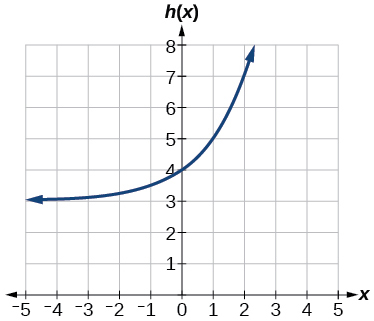
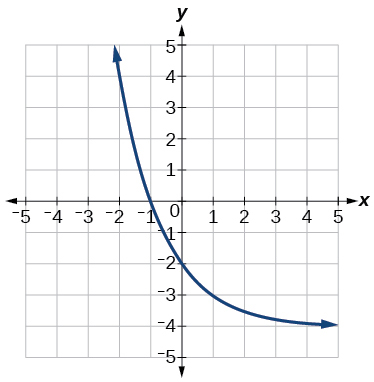
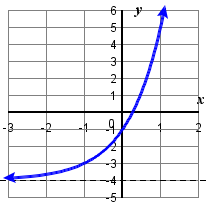
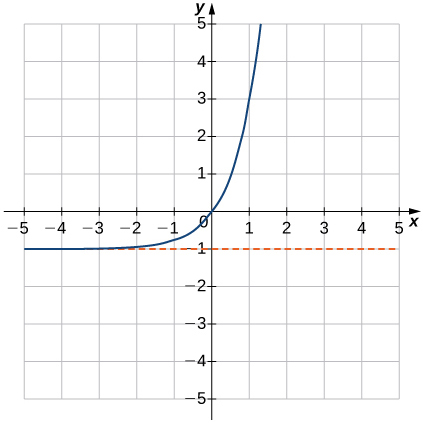
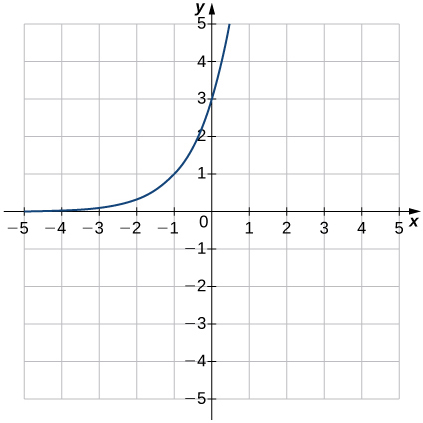
\( \bigstar \) In the following exercises, match the graphs to one of the following functions:
| a. \(2^{x}\) | b. \(2^{x+1}\) | c. \(2^{x-1}\) | d. \(2^{x}+2\) | e. \(2^{x}-2\) | f. \(3^{x}\) |
|
17.
|
18.
|
19.
|
|
20.
|
21.
|
22.
|
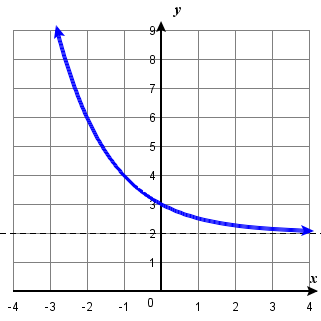
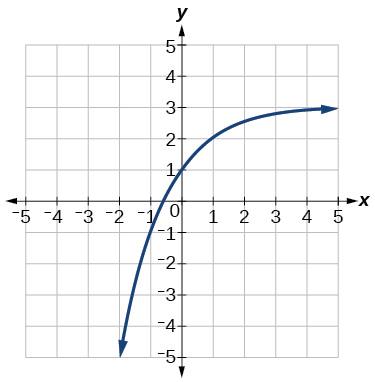
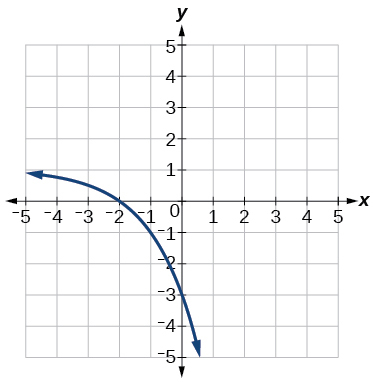
\( \bigstar \) For the following exercises, match the exponential equation to the correct graph.
| a. \(y=4^{−x}\) | b. \(y=3^{x−1}\) | c. \(y=2^{x+1}\) | d. \(y=(\frac{1}{2})^x+2\) | e. \(y=−3^{−x}\) | f. \(y=1−5^x\) |
|
23)
|
24)
|
25)
|
|
26)
|
27)
|
28)
|
- Answers to odd exercises:
-
17. f, 19. a, 21. e; 23. d, 25. b, 27. e
C: Graph Basic Exponential Functions
Exercise \(\PageIndex{C}\)
\( \bigstar \) In the following exercises, graph each exponential function.
|
29. \(f(x)=2^{x}\) 30. \(g(x)=3^{x}\) 31. \(f(x)=6^{x}\) 32. \(g(x)=7^{x}\) |
33. \(f(x)=(1.5)^{x}\) 34. \(g(x)=(2.5)^{x}\) 35. \(f(x)=\left(\frac{1}{2}\right)^{x}\) 36. \(g(x)=\left(\frac{1}{3}\right)^{x}\) |
37. \(f(x)=\left(\frac{1}{6}\right)^{x}\) 38. \(g(x)=\left(\frac{1}{7}\right)^{x}\) 39. \(f(x)=(0.4)^{x}\) 40. \(g(x)=(0.6)^{x}\) |
41. \(f(x)=4^{x}\) 42. \(g(x)=5^{x}\) 43. \(f(x)=\left(\frac{1}{4}\right)^{x}\) 44. \(h(x)=\left(\frac{1}{5}\right)^{x}\) |
- Answers to odd exercises:
-
29.
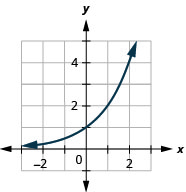
\(f(x)=2^{x}\) 31.
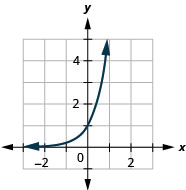
\(f(x)=6^{x}\) 33.
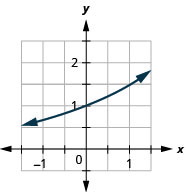
\(f(x)=(1.5)^{x}\) 35.
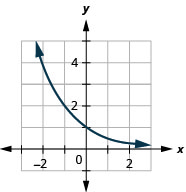
\(f(x)=\left(\frac{1}{2}\right)^{x}\) 37.
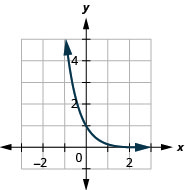
\(f(x)=\left(\frac{1}{6}\right)^{x}\) 39.
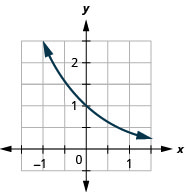
\(f(x)=(0.4)^{x}\) 41.
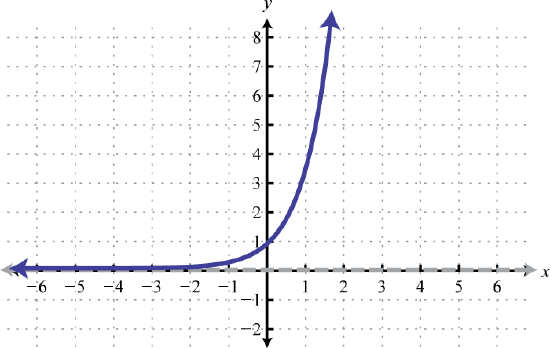
\(f(x)=4^{x}\) 43.
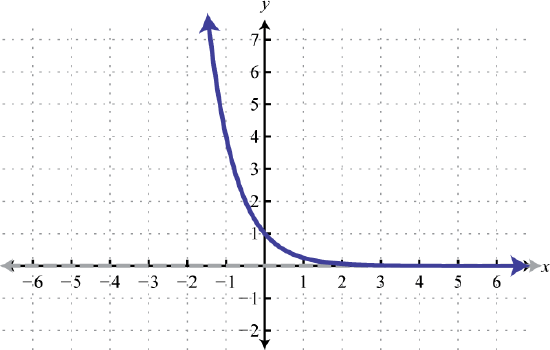
\(f(x)=\left(\frac{1}{4}\right)^{x}\)
D: Graph Shifts of Exponential Functions
Exercise \(\PageIndex{D}\)
\( \bigstar \) In the following exercises, use transformations to graph each exponential function. State the transformations that must be done to the parent function in order to obtain the graph.
|
45. \( g(x)=2^{x}+1\) 46.\( g(x)=2^{x}-1\) 47. \( g(x)=2^{x-2}\) 48. \( g(x)=2^{x+2}\) |
49. \(g(x)=3^{x}+2\) 50. \(f(x)=3^{x}-6\) 51. \( g(x)=4^{x-1}\) 52. \(f(x)=4^{x+2}\) |
53. \(f(x)=2^{x}+3\) 54. \(f(x)=2^{x}-3\) 55. \(f(x)=3^{x+2}\) 56. \(f(x)=3^{x+1}\) |
57. \(h(x)=2^{x-3}-2\) 58. \(g(x)=3^{x-1}+3\) 59. \(f(x)=3^{x+1}-4\) 60. \(h(x)=3^{x-2}+4\) |
61. \(f(x)=4^{x}+2\) 62. \(f(x)=4^x−1\) 63. \(f(x)=5^{x+1}+2\) 64. \(f(x)=10^{x-4}+2\) |
- Answers to odd exercises:
-
45. Up 1
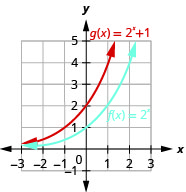\(g(x)=2^{x}+1\)47. Right 2
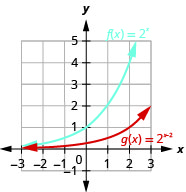
\( g(x)=2^{x-2}\) 49. Up 2
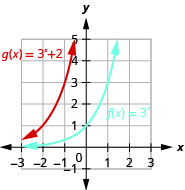
\(g(x)=3^{x}+2\) 51. Right 1
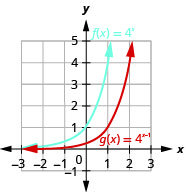
\(g(x)=4^{x-1}\) 53. Up 3
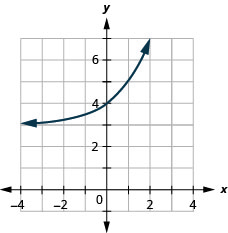
\(f(x)=2^{x}+3\) 55. Left 2
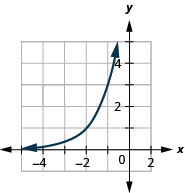
\(f(x)=3^{x+2}\) 57. Right 3, Down 2;
Domain: \((-\infty, \infty)\); Range: \((-2, \infty)\)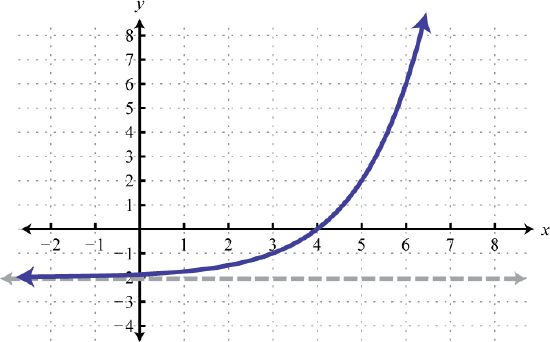
\(h(x)=2^{x-3}-2\) 59. Left 1, Down 4;
Domain: \((-\infty, \infty)\); Range: \((-4, \infty)\)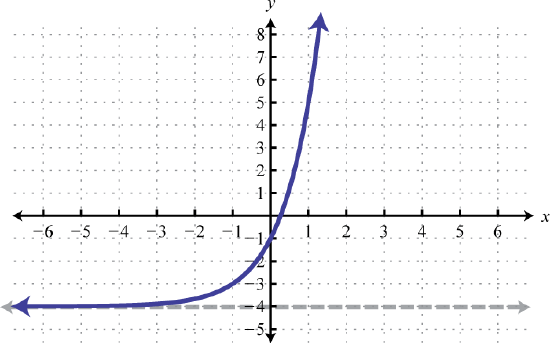
\(f(x)=3^{x+1}-4\) 61. up 2; Domain: \((-\infty, \infty)\); Range: \((2, \infty)\)
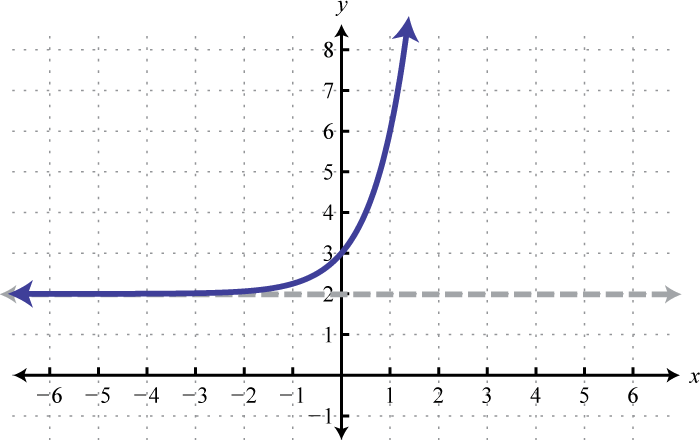
\(f(x)=4^{x}+2\) 63. Left 1, up 2
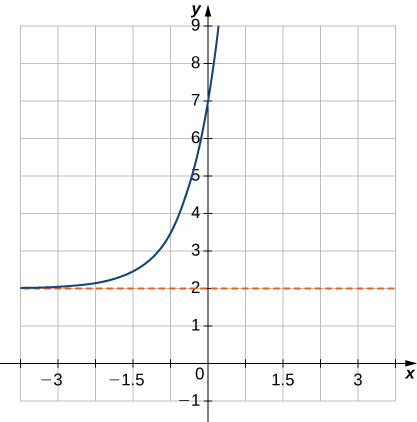
63. \(f(x)=5^{x+1}+2\)
\( \bigstar \) In the following exercises, use transformations to graph each exponential function. State the transformations that must be done to the parent function in order to obtain the graph.
|
65. \(f(x)=\left(\frac{1}{2}\right)^{x-4}\) 66. \(f(x)=\left(\frac{1}{2}\right)^{x}-3\) |
67. \(f(x)=\left(\frac{1}{4}\right)^{x}-2\) 68. \(h(x)=\left(\frac{1}{3}\right)^{x}+2\) |
69. \(f(x)=e^{x}-3\) 70. \(f(x)=e^{x}+2\) 71. \(f(x)=e^{x}+1\) |
72. \(f(x)=e^{x-2}\) 73. \(f(x)=e^{x+1}\) 74. \(f(x)=e^{x-3}\) |
75. \(f(x)=e^{x-2}+1\) 76. \(f(x)=e^{x+2}-1\) |
- Answers to odd exercises:
-
65. Right 4
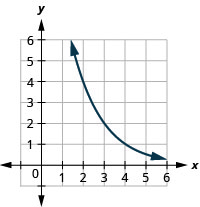
\(f(x)=\left(\frac{1}{2}\right)^{x-4}\) 67. Down 2; Domain: \((-\infty, \infty)\); Range: \((-2, \infty)\)
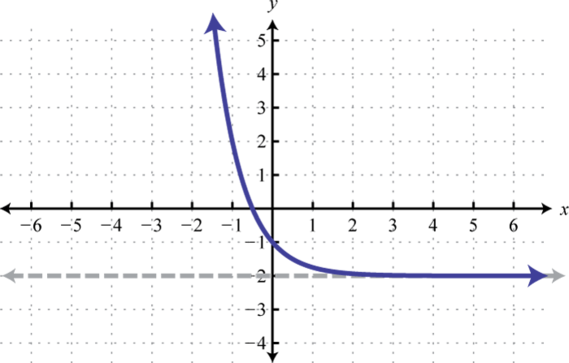
\(f(x)=\left(\frac{1}{4}\right)^{x}-2\) 69. Down 3. Domain: \((-\infty, \infty)\); Range: \((-3, \infty)\)
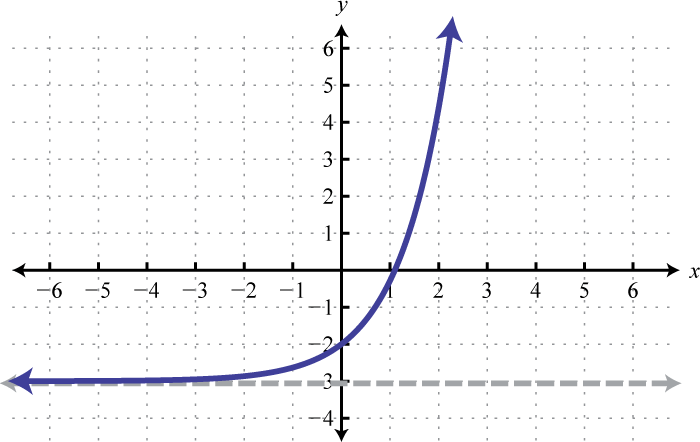
\(f(x)=e^{x}-3\) 71. Up 1
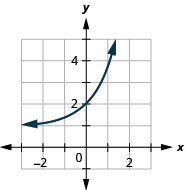
\(f(x)=e^{x}+1\) 73. Left 1; Domain: \((-\infty, \infty)\); Range: \((0, \infty)\)
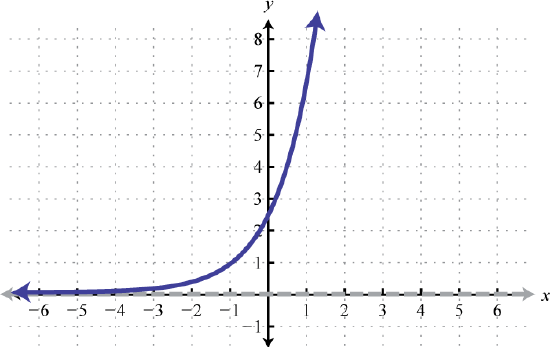
\(f(x)=e^{x+1}\) 75. Right 2, up 1; Domain: \((-\infty, \infty)\); Range: \((1, \infty)\)
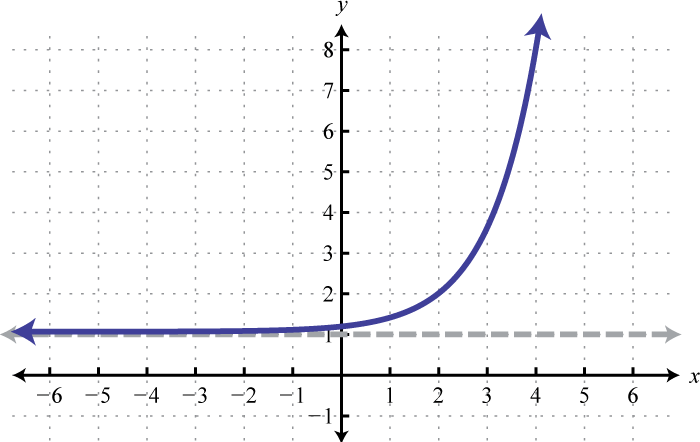
\(f(x)=e^{x-2}+1\)
E: Graph Reflections and Stretches of Exponential Functions
Exercise \(\PageIndex{E}\)
\( \bigstar \) In the following exercises, graph each exponential function. State the transformations that must be done to the parent function in order to obtain the graph and state its domain, range, and horizontal asymptote.
|
77. \(f(x)=-2^{x}\) 78. \(f(x)=2^{-x-1}-1\) 79. \(g(x)=2^{-x}-3\) 80. \(g(x)=3^{-x}+1\) |
81. \(f(x)=6-10^{-x}\) 82. \(g(x)=5-4^{-x}\) 83. \(f(x)=5-2^{x}\) 84. \(f(x)=3-3^{x}\) |
84.1 \(f(x) = 3 \cdot 2^{x-4}-5 \) 84.2 \(y = 5-\frac{1}{2} \cdot 4^{x-3} \) 84.3 \(f(x) = 3^{x/2+3}-4\) 84.4 \(f(x) = 5-2^{-x/3+1}\) |
85) \(f(x)=1−2^{−x}\) 86) \(f(x)=2^{-x}\) 87. \(g(x)=-e^{x}\) 88. \(g(x)=e^{-x}\) |
89. \(h(x)=-e^{x+1}\) 90. \(h(x)=-e^{x}+3\) 91) \(f(x)=e^{−x}−1\) |
\( \bigstar \) For the following exercises, graph each set of functions on the same axes.
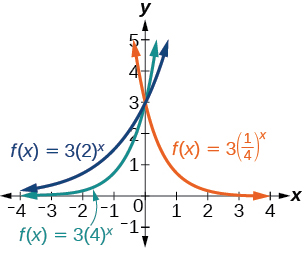
| 93) \(f(x)=3\left ( \frac{1}{4} \right )^x, g(x)=3(2)^x, h(x)=3(4)^x\) | 94) \(f(x)=\frac{1}{4}(3)^x, g(x)=2(3)^x, h(x)=4(3)^x\) |
\( \bigstar \) For the following exercises, describe the end behavior of the graphs of the functions and the transformations needed to do on the parent graph to obtain the graph of the function.
| 95) \(f(x)=-5(4)^x-1\) | 96) \(f(x)=3\left ( \frac{1}{2} \right )^x-2\) | 97) \(f(x)=3(4)^{-x}+2\) |
- Answers to odd exercises:
-
77. Reflect over x-axis
HA: y = 0
Domain: \((-\infty, \infty)\); Range: \((-\infty, 0)\)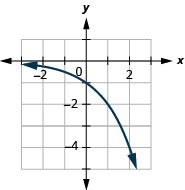
\(f(x)=-2^{x}\) 79. Reflect over y-axis, down 3;
HA: y = -3
Domain: \((-\infty, \infty)\); Range: \((-3, \infty)\)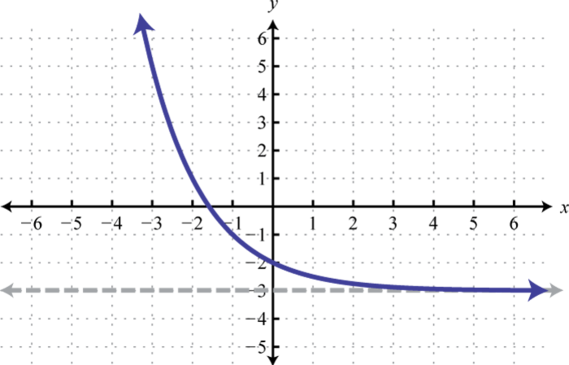
\(g(x)=2^{-x}-3\) 81. Reflect over y-axis, reflect over x-axis, up 6; HA: y = 6; Domain: \((-\infty, \infty)\); Range: \((-\infty, 6)\)
\(f(x)=6-10^{-x}\) 83. Reflect over x-axis, up 5; HA: y = 5; Domain: \((-\infty, \infty)\); Range: \((-\infty, 5)\)
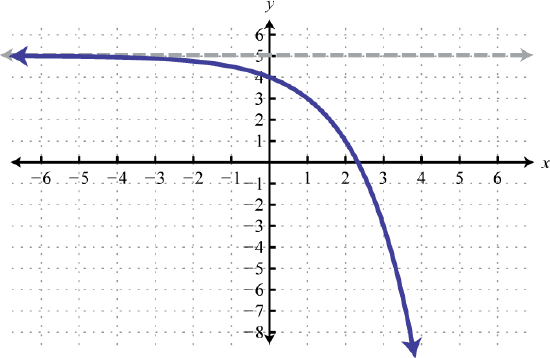
\(f(x)=5-2^{x}\) 85. Reflect over y-axis, repfect over x-axis up 1; HA: y=1; Domain: all real numbers, range: \((−∞,1) \)
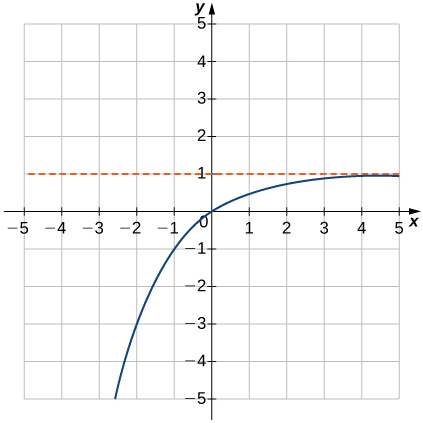\(f(x)=1−2^{−x}\)87. Reflect over x-axis; HA: y = 0; Domain: \((-\infty, \infty)\); Range: \((-\infty, 0)\)
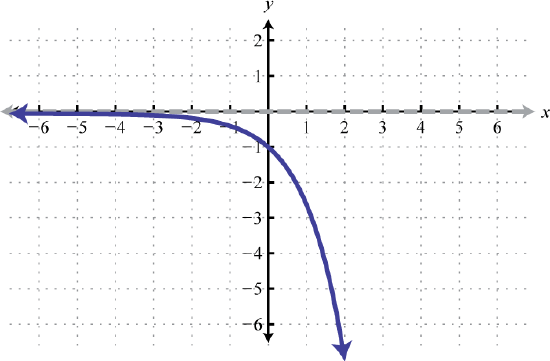
\(g(x)=-e^{x}\) 89. Left 1, Reflect over x-axis; HA: y=0; Domain: \((-\infty, \infty)\); Range: \((-\infty, 0)\)
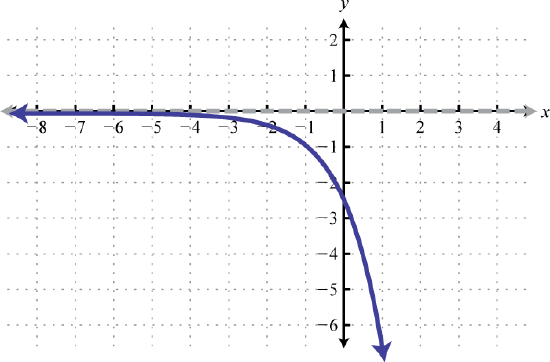
\(h(x)=-e^{x+1}\) 91. Reflect over y-axis, down 1; HA: y = -1; Domain: all real numbers, range: \((−1,∞)\)
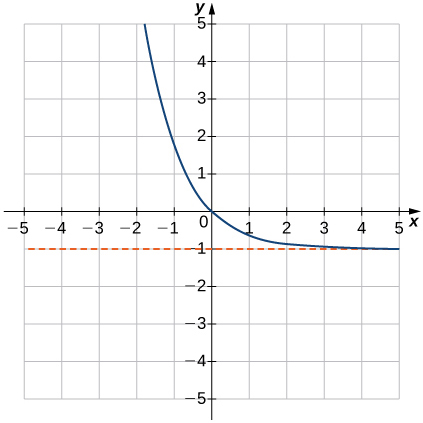
\(f(x)=e^{−x}−1\) 93.
95. As \(x\rightarrow \infty , f(x)\rightarrow -\infty\); As \(x\rightarrow -\infty , f(x)\rightarrow -1\); Reflect over x-axis, y's stretched by a factor of 5, down 1
97. As \(x\rightarrow \infty , f(x)\rightarrow 2\); As \(x\rightarrow -\infty , f(x)\rightarrow \infty\); Reflect over y-axis, y's get stretched by a factor of 3, up 2.
F: Construct an Equation Given a Description
Exercise \(\PageIndex{F}\)
\( \bigstar \) For the following exercises, start with the graph of \(f(x)=4^x\). Then write a function that results from the given transformation.
|
98) Shift \(f(x)\) \(4\) units upward 99) Shift \(f(x)\) \(3\) units downward |
100) Shift \(f(x)\) \(2\) units left 101) Shift \(f(x)\) \(5\) units right |
102) Reflect \(f(x)\) about the \(x\)-axis 103) Reflect \(f(x)\) about the \(y\)-axis |
\( \bigstar \) For the following exercises, (a) graph the function, (b) graph its reflection about the \(y\)-axis and construct the function for the reflected graph, and (c) give the \(y\)-intercept.
| 104) \(f(x)=3\left ( \frac{1}{2} \right )^x\) | 105) \(g(x)=-2(0.25)^x\) | 106) \(h(x)=6(1.75)^{-x}\) |
\( \bigstar \) For the following exercises, (a) graph the function, (b) graph its reflection about the \(x\)-axis and construct the function for the reflected graph.
| 107) \(f(x)=\frac{1}{2}(4)^x\) | 108) \(f(x)=3(0.75)^x-1\) | 109) \(f(x)=-4(2)^x+2\) |
\( \bigstar \) For the following exercises, (a) construct the equation of the exponential function given a description. (b) State its \(y\)-intercept, domain, and range.
111) The graph of \(f(x)=10^x\) is reflected about the \(x\)-axis and shifted upward \(7\) units. What is the equation of the new function, \(g(x)\)? State its \(y\)-intercept, domain, and range.
112) The graph of \(f(x)=\left ( \frac{1}{2} \right )^{-x}\) is reflected about the \(y\)-axis and compressed vertically by a factor of \(\left ( \frac{1}{5} \right )\) What is the equation of the new function, \(g(x)\) State its \(y\)-intercept, domain, and range.
113) The graph of \(f(x) = 3^x\) is reflected about the \(y\)-axis and stretched vertically by a factor of \(4\). What is the equation of the new function, \(g(x)\). State its \(y\)-intercept, domain, and range.
114) The graph of \(f(x)=(1.68)^x\) is shifted right \(3\) units, stretched vertically by a factor of \(2\), reflected about the \(x\)-axis, and then shifted downward \(3\) units. What is the equation of the new function, \(g(x)\)? State its \(y\)-intercept (to the nearest thousandth), domain, and range.
115) The graph of \(f(x)=2\left ( \frac{1}{4} \right )^{x-1}\) is shifted left \(2\) units, stretched vertically by a factor of \(4\), reflected about the \(x\)-axis, and then shifted downward \(4\) units. What is the equation of the new function, \(g(x)\)? State the y-intercept, domain, and range of \(g(x)\).
- Answers to odd exercises:
-
99. \(f(x)=4^x-3\) \(\qquad\) 101. \(f(x)=4^{x-5}\) \(\qquad\) 103. \(f(x)=4^{-x}\)
105.
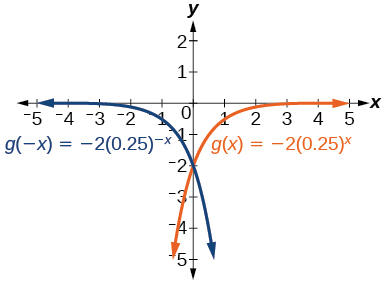
\(y\)-intercept: \((0,-2)\)
107
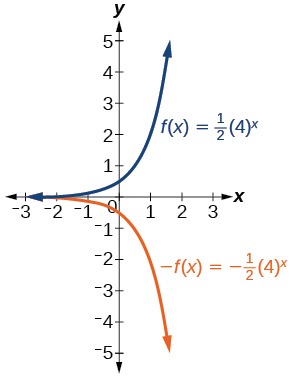
109
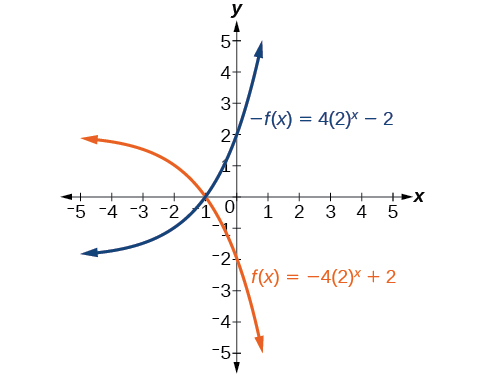
111. \(g(x)=-10^x + 7\); \(y\)-intercept: \((0,6)\); Domain: all real numbers; Range: all real numbers less than \(7\).
113. \(g(x)=4(3)^{-x}\) \((0,4)\) Domain: all real numbers; Range: all real numbers greater than \(0\).
115. \(g(x)=-8 \left ( \frac{1}{4} \right )^{x+1} -4\); \(y\)-intercept: \((0,-6)\); Domain: \((-\infty, \infty)\); Range: \((-\infty, -4)\)
G: Construct an Equation Given a Graph
Exercise \(\PageIndex{G}\)
\( \bigstar \) Write an equation for each of the functions graphed below. The graphs #117-123 are transformations of the parent function \(f(x)=2^x\). The parent functions for #124-127 must be determined.
|
117.
|
118.
|
119.
|
120.  |
|
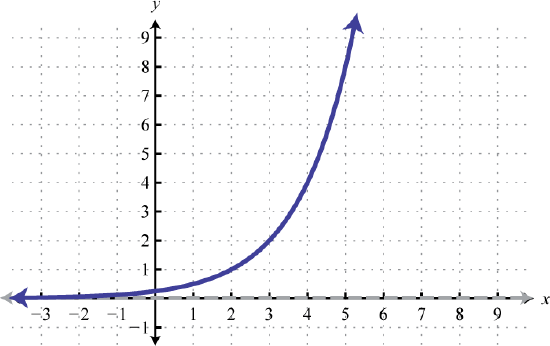121.
|
122.
|
123.
|
124.
|
|
125.
|
126.
|
127. (Hint: this graph has been stretched)
|
|
- Answer to odd exercises:
-
117. \(y=-2^x+3\)
119. \(y=2^x+3\)
121. \(y=-2^{-x+1}+3\)
123. \(y=2^{-x+1}-4\)
125. \(y=4^x-1\)
127. \(y=-2(3)^x+7\)
H: Practice with Exponent Properties
Exercise \(\PageIndex{H}\)
\( \bigstar \) Write the following with only one exponent, \(x\). Simplify.
|
|
|
|
|
|
- Answers to odd exercises:
-
131. \( 8(2^x) \quad \) 133. \( \dfrac{4^x}{64} \quad \) 135. \( \dfrac{256}{4^x} = 256 \left( \dfrac{1}{4} \right)^x \quad \) 137. \( 25^x \quad \) 139. \(35^x \) \(\quad\) 141. \( 18^x \quad \) 143. \(4(8^x) \)
145. \( \dfrac{64^x}{16} \quad \) 147. \( \dfrac{3}{8}24^x \quad \) 149. \(\left( \dfrac{3}{5} \right)^x\) \(\quad\) 151. \( 2^x \quad \) 153. \(24 \left( \dfrac{3}{4} \right)^x \quad \) 155. \(\dfrac{9}{16} \left( \dfrac{3}{8} \right)^x \)