4.6: Exponential and Logarithmic Equations

Learning Objectives

• Solve exponential equations by rewriting with a common base, or rewriting in logarithmic form. 
• Solve logarithmic equations by rewriting in exponential form or using the one-to-one property of logarithms.

In 1859, an Australian landowner named Thomas Austin released \(24\) rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.

Solve Exponential Equations

Use the One-to-One Property of Exponential Functions

The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers \(b\), \(S\), and \(T\), where \(b>0\), \(b≠1\), \(b^S=b^T\) if and only if \(S=T\).

In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.

For example, consider the equation \(3^{4x−7}=\dfrac{3^{2x}}{3}\). To solve for \(x\), we use the division property of exponents to rewrite the right side so that both sides have the common base, \(3\). Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for \(x\):

\[\begin{align*} 3^{4x-7}&= \dfrac{3^{2x}}{3}\\ 3^{4x-7}&= \dfrac{3^{2x}}{3^1} \qquad &&\text{Rewrite 3 as } 3^1\\ 3^{4x-7}&= 3^{2x-1} \qquad &&\text{Use the division property of exponents}\\ 4x-7&= 2x-1 \qquad &&\text{Apply the one-to-one property of exponents}\\ 2x&= 6 \qquad &&\text{Subtract 2x and add 7 to both sides}\\ x&= 3 \qquad &&\text{Divide by 3} \end{align*}\]

THE 1-1 PROPERTY OF EXPONENTIAL FUNCTIONS

For any algebraic expressions \(S\) and \(T\), and any positive real number \(b≠1\),

\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]

 How to: Solve an exponential equation of the form \(b^S=b^T\), where \(S\) and \(T\) are algebraic expressions.

1. Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form \(b^S=b^T\).
2. Use the one-to-one property to set the exponents equal.
3. Solve the resulting equation, \(S=T\), for the unknown.

Example \(\PageIndex{1}\): Solve an Exponential Equation with a Common Base

Solve \(2^{x−1}=2^{2x−4}\).

Solution

\[\begin{align*} 2^{x-1}&= 2^{2x-4} \qquad &&\text{The common base is 2}\\ x-1&= 2x-4 \qquad &&\text{By the one-to-one property the exponents must be equal}\\ x&= 3 \qquad &&\text{Solve for x} \end{align*}\]

 Try It \(\PageIndex{1}\)

Solve \(5^{2x}=5^{3x+2}\).

Answer

\(x=−2\)

Common Base Method

Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.

For example, consider the equation \(256=4^{x−5}\). We can rewrite both sides of this equation as a power of \(2\). Then we apply the rules of exponents, along with the one-to-one property, to solve for \(x\):

\[\begin{align*} 256&= 4^{x-5}\\ 2^8&= {(2^2)}^{x-5} \qquad &&\text{Rewrite each side as a power with base 2}\\ 2^8&= 2^{2x-10} \qquad &&\text{Use the one-to-one property of exponents}\\ 8&= 2x-10 \qquad &&\text{Apply the one-to-one property of exponents}\\ 18&= 2x \qquad &&\text{Add 10 to both sides}\\ x&= 9 \qquad &&\text{Divide by 2} \end{align*}\]

 How to: Given an exponential equation with unlike bases, use the one-to-one property to solve it.

1. Rewrite each side in the equation as a power with a common base.
2. Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form \(b^S=b^T\).
3. Use the one-to-one property to set the exponents equal.
4. Solve the resulting equation, \(S=T\), for the unknown.

Example \(\PageIndex{2}\): Solve Equations by Rewriting Them to Have a Common Base

Solve \(8^{x+2}={16}^{x+1}\).

Solution

\[\begin{align*} 8^{x+2}&= {16}^{x+1}\\ {(2^3)}^{x+2}&= {(2^4)}^{x+1} \qquad &&\text{Write 8 and 16 as powers of 2}\\ 2^{3x+6}&= 2^{4x+4} \qquad &&\text{To take a power of a power, multiply exponents}\\ 3x+6&= 4x+4 \qquad &&\text{Use the one-to-one property to set the exponents equal}\\ x&= 2 \qquad &&\text{Solve for } x \end{align*}\]

 Try It \(\PageIndex{2}\)

Solve \(5^{2x}={25}^{3x+2}\).

Answer

\(x=−1\)

 \(\PageIndex{3}\)

Solve \(2^{5x}=\sqrt{2}\).

Solution

\[\begin{align*} 2^{5x}&= 2^{\frac{1}{2}} \qquad &&\text{Write the square root of 2 as a power of 2}\\ 5x&= \dfrac{1}{2} \qquad &&\text{Use the one-to-one property}\\ x&= \dfrac{1}{10} \qquad &&\text{Solve for } x \end{align*}\]

 Try It \(\PageIndex{3}\)

Solve \(5^x=\sqrt{5}\).

Answer

\(x=\dfrac{1}{2}\)

Do all exponential equations have a solution? How can we tell if there is not a solution?

No. Recall that the range of an exponential function is always positive. In the process of solving an exponential equation, if the equation obtained is an exponential expression that is not equal to a positive number, there is no solution for that equation.

Example \(\PageIndex{4}\): Exponential Equation with no solution

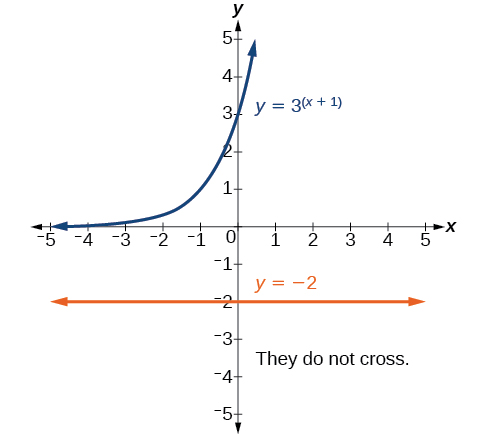
Solve \(3^{x+1}=−2\).

Solution

This equation has no solution. There is no real value of \(x\) that will make the equation a true statement because any power of a positive number is positive. The figure below shows that the two graphs do not cross so the left side of the equation is never equal to the right side. Thus the equation has no solution.

Figure \(\PageIndex{4}\)

 Try It \(\PageIndex{4}\)

Solve \(2^x=−100\).

Answer

The equation has no solution.

Rewrite in Logarithmic Form 

Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since \(\log(a)=\log(b)\) is equivalent to \(a=b\), we may apply logarithms with the same base on both sides of an exponential equation.

 How to: Solve an exponential equation in which a common base cannot be found

1. Apply the logarithm to both sides of the equation.
   • If one of the terms in the equation has base 10, use the common logarithm.
   • If one of the terms in the equation has base \(e\), use the natural logarithm.
2. Use the rules of logarithms to solve for the unknown.

Example \(\PageIndex{5}\): Solve an Equation Containing Powers of Different Bases

Solve \(5^{x+2}=4^x\).

Solution

\[\begin{align*}
5^{x+2}&= 4^x \qquad &&\text{There is no easy way to get the powers to have the same base}\\
\ln5^{x+2}&= \ln4^x \qquad &&\text{Take ln of both sides}\\
(x+2)\ln5&= x\ln4 \qquad &&\text{Power Rule for Logarithms}\\
x\ln5+2\ln5&= x\ln4 \qquad &&\text{Use the distributive law}\\
x\ln5-x\ln4&= -2\ln5 \qquad &&\text{Get terms containing x on one side, terms without x on the other}\\
x(\ln5-\ln4)&= -2\ln5 \qquad &&\text{On the left hand side, factor out an x}\\
x\ln \left (\frac{5}{4} \right )&= \ln \left (\frac{1}{25} \right ) \qquad &&\text{Power and Quotient Rules for Logarithms}\\
x&=\dfrac{\ln \left (\dfrac{1}{25} \right )}{\ln \left (\dfrac{5}{4} \right )} \qquad &&\text{Divide by the coefficient of x}
\end{align*}\]

 Try It \(\PageIndex{5}\)

Solve \(2^x=3^{x+1}\).

Answer

\(x=\dfrac{\ln3}{\ln \left (\dfrac{2}{3} \right )}\)

Is there any way to solve \(2^x=3^x\)?

Yes. The solution is \(x = 0\). (Take the \( \ln \) of both sides, use the power rule, and solve for \(x\)).

Equations Containing \(e\)

One common type of exponential equations are those with base \(e\). This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base \(e\) on either side, we can use the natural logarithm to solve it.

 How to: Given an equation of the form \(y=Ae^{kt}\), solve for \(t\).

1. Divide both sides of the equation by \(A\).
2. Apply the natural logarithm of both sides of the equation.
3. Divide both sides of the equation by \(k\).

Example \(\PageIndex{6}\): Solve an Equation of the Form \(y = Ae^{kt}\)

Solve \(100=20e^{2t}\).

Solution

\[\begin{align*} 100&= 20e^{2t}\\ 5&= e^{2t} \qquad &&\text{Divide by the coefficient of the power}\\ \ln5&= 2t \qquad &&\text{Take ln of both sides. Use the fact that } ln(x) \text{ and } e^x \text{ are inverse functions}\\ t&= \dfrac{\ln5}{2} \qquad &&\text{Divide by the coefficient of t} \end{align*}\]

Analysis

Using logarithm rules, this answer can be rewritten in the form \(t=\ln\sqrt{5}\). A calculator can be used to obtain a decimal approximation of the answer, \( t \approx 0.8047 \).

 Try It \(\PageIndex{6}\)

Solve \(3e^{0.5t}=11\).

Answer

\(t=2\ln \left (\dfrac{11}{3} \right )\) or \(\ln{ \left (\dfrac{11}{3} \right )}^2\)

Does every equation of the form \(y=Ae^{kt}\) have a solution?

No. When \(k≠0\), there is a solution when \(y\) and \(A\) are either both 0, or when neither is 0 and they have the same sign. An example of an equation with this form that does not have a solution is \(2=−3e^t\), which would mean \(e^t\) is negative, which is impossible.

Example \(\PageIndex{7}\): Solve an Equation That Can Be Simplified to the Form \(y=Ae^{kt}\)

Solve \(4e^{2x}+5=12\).

Solution

\[\begin{align*} 4e^{2x}+5&= 12\\ 4e^{2x}&= 7 \qquad &&\text{Combine like terms}\\ e^{2x}&= \dfrac{7}{4} \qquad &&\text{Divide by the coefficient of the power}\\ 2x&= \ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Take ln of both sides and use }\ln e^u = u\\ x&= \dfrac{1}{2}\ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Solve for x} \end{align*}\]

 Try It \(\PageIndex{7}\)

Solve \(3+e^{2t}=7e^{2t}\).

Answer

\(t=\ln \left (\dfrac{1}{\sqrt{2}} \right )=−\dfrac{1}{2}\ln(2)\)

Use properties of exponents

Being able to solve equations of the form \(y=Ae^{kt}\) suggests a final way of solving exponential equations that can be rewritten in the form \( a = b^{p(x)} \). We will redo example 5 using this alternate method. The method used in example 5 is good practice using log properties. This alternative approach uses exponent properties instead.

 How to: Solve an exponential equation in which a common base cannot be found

1. If possible, use Rules of Exponents to write the equation in the form \( a = b^{p(x)} \). 
2. Rewrite the exponential equation in its logarithmic form: \(p(x) = \log_b (a) \), and solve for \(x\).

Example \(\PageIndex{8}\): Simplify using Exponent Rules before writing in Logarithmic form

Solve \(5^{x+2}=4^x\).

Solution

\[\begin{align*}
5^{x+2}&= 4^x \qquad &&\text{Use the Exponent Product Rule in reverse}\\
5^x \cdot 5^2 &= 4^x \qquad &&\text{ }\\
5^x \cdot 25   &= 4^x \qquad &&\text{ }\\
25    &= \dfrac{4^x}{5^x} \qquad &&\text{Like Powers Rule }\\
25    &= \left(\frac{4}{5}\right)^x \qquad &&\text{Rewrite as a log equation}\\
x &= \log_\ce{4/5} (25) \qquad &&\text{Now use the change of base rule}\\
x &= \dfrac{\ln 25}{\ln \ce{4/5}} \approx -14.4251
\end{align*}\]

Exponential Equations that are quadratic in form

Extraneous Solutions

Sometimes the methods used to solve an equation introduce an extraneous solution, which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the value of the argument of a logarithm is negative, there is no output.

Example \(\PageIndex{9}\): Solve Exponential Functions that are Quadratic in Form

Solve \(e^{2x}−e^x=56\).

Solution:

\[\begin{align*} e^{2x}-e^x&= 56\\
e^{2x}-e^x-56&= 0 \qquad &&\text{Get one side of the equation equal to zero}\\
(e^x+7)(e^x-8)&= 0 \qquad &&\text{Factor by the FOIL method}\\
{\begin{array} {rl}
e^x+7&= 0  \\
e^x&= -7\\
x &= \text{undefined} \\
\end{array}} & { \begin{array} {rl}
\qquad e^x-8&= 0 \\
e^x&= 8 \\
x &= \ln 8 \\
\end{array} } && { \begin{array} {l}
\text{Use the Zero Factor Property to solve for } x \\
\text{Rewrite in log form } \\
\text{Reject the equation in which the power equals a negative number }
\end{array} } \\
 \end{align*}\]

Analysis

When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation \(e^x=−7\) because a positive number never equals a negative number. The solution \(\ln(−7)\) is not a real number, and in the real number system this solution is rejected as an extraneous solution.

 Try It \(\PageIndex{9}\)

Solve \(e^{2x}=e^x+2\).

Answer

\(x=\ln2\)

 Solving Logarithmic Equations

Does every logarithmic equation have a solution?

No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.

Rewrite in Exponential Form

We have already seen that every logarithmic equation \({\log}_b(x)=y\) is equivalent to the exponential equation \(b^y=x\). We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation \({\log}_2(2)+{\log}_2(3x−5)=3\). To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then rewrite the logarithmic equation in exponential form to solve for \(x\):

\[\begin{align*} {\log}_2(2)+{\log}_2(3x-5)&= 3\\ {\log}_2(2(3x-5))&= 3 \qquad &&\text{Apply the product rule of logarithms}\\ {\log}_2(6x-10)&= 3 \qquad &&\text{Distribute}\\ 2^3&= 6x-10 \qquad &&\text{Apply the definition of a logarithm}\\ 8&= 6x-10 \qquad &&\text{Calculate } 2^3\\ 18&= 6x \qquad &&\text{Add 10 to both sides}\\ x&= 3 \qquad &&\text{Divide by 6, then check the solution!} \end{align*}\]

Whenever solving an equation with logarithms, it is always necessary to check that the solution is in the domain of the original equation. If it is not, it must be rejected as a solution.

USE THE DEFINITION OF A LOGARITHM TO SOLVE LOGARITHMIC EQUATIONS

For any algebraic expression \(S\) and real numbers \(b\) and \(c\), where \(b>0\), \(b≠1\),

\[\begin{align} {\log}_b(S)=c \text{ if and only if } b^c=S \end{align}\]

Example \(\PageIndex{10}\): Rewrite a Logarithmic Equation in Exponential Form

Solve \(2\ln x+3=7\).

Solution

\[\begin{align*} 2\ln x+3&= 7\\ 2\ln x&= 4 \qquad &&\text{Subtract 3}\\ \ln x&= 2 \qquad &&\text{Divide by 2}\\ x&= e^2 \qquad &&\text{Rewrite in exponential form} \end{align*}\]

 Try It \(\PageIndex{10}\)

Solve \(6+\ln x=10\).

Answer

\(x=e^4\)

Example \(\PageIndex{11}\) 

Solve \(2\ln(6x)=7\).

Solution:

\[\begin{align*} 2\ln(6x)&= 7\\ \ln(6x)&= \dfrac{7}{2} \qquad &&\text{Divide by 2}\\ 6x&= e^{\left (\dfrac{7}{2} \right )} \qquad &&\text{Use the definition of }\ln \\ x&= \tfrac{1}{6}e^{\left (\tfrac{7}{2} \right )} &&\qquad \text{Divide by 6} \end{align*}\]

 Try It \(\PageIndex{11}\)

Solve \(2\ln(x+1)=10\).

Answer

\(x=e^5−1\)

Use the One-to-One Property of Logarithms

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers \(S>0\), \(T>0\) and any positive real number \(b\), where \(b≠1\),

\({\log}_bS={\log}_bT\) if and only if \(S=T\).

For example,

If \({\log}_2(x−1)={\log}_2(8)\), then \(x−1=8\).

So, if \(x−1=8\), then we can solve for \(x\), and we get \(x=9\). To check, we can substitute \(x=9\) into the original equation: \({\log}_2(9−1)={\log}_2(8)=3.\) In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation \(\log(3x−2)−\log(2)=\log(x+4)\). To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for \(x\):

\[\begin{align*} \log(3x-2)-\log(2)&= \log(x+4)\\ \log \left (\dfrac{3x-2}{2} \right )&= \log(x+4) \qquad &&\text{Apply the quotient rule of logarithms}\\ \dfrac{3x-2}{2}&= x+4 \qquad &&\text{Apply the one to one property of a logarithm}\\ 3x-2&= 2x+8 \qquad &&\text{Multiply both sides of the equation by 2}\\ x&= 10 \qquad &&\text{Subtract 2x and add 2} \end{align*}\]

To check the result, substitute \(x=10\) into \(\log(3x−2)−\log(2)=\log(x+4)\).

\[\begin{align*} \log(3(10)-2)-\log(2)&= \log((10)+4) \\ \log(28)-\log(2)&= \log(14)\\ \log \left (\dfrac{28}{2} \right )&= \log(14) \qquad \text{The solution checks} \end{align*}\]

USE THE ONE-TO-ONE PROPERTY OF LOGARITHMS TO SOLVE LOGARITHMIC EQUATIONS

For any algebraic expressions \(S\) and \(T\) and any positive real number \(b\), where \(b≠1\),

\[\begin{align*} {\log}_bS={\log}_bT \quad \text{ if and only if } \quad S=T \end{align*}\]

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

 How to: Given an equation containing logarithms, solve it using the one-to-one property

1. Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form \({\log}_bS={\log}_bT\).
2. Use the one-to-one property to set the arguments equal.
3. Solve the resulting equation, \(S=T\), for the unknown.
4. Confirm that each solution is correct. If a solution when substituted in the original equation makes one of the log arguments zero or negative, that solution must be rejected.

Example \(\PageIndex{12}\): Use the One-to-One Property of Logarithms to Solve an Equation

Solve \(\ln(x^2)=\ln(2x+3)\).

Solution

\[\begin{align*} \ln(x^2)&= \ln(2x+3)\\ x^2&= 2x+3 \qquad &&\text{Use the one-to-one property of the logarithm}\\ x^2-2x-3&= 0 \qquad &&\text{Get zero on one side before factoring}\\ (x-3)(x+1)&= 0 \qquad &&\text{Factor using FOIL}\\
x-3 = 0 \qquad \quad & \text{or} \qquad x+1=0 &&\text{If a product is zero, one of the factors must be zero}\\
x=3 \qquad \quad &\quad  \qquad x= -1 \qquad &&\text{Solve for x}\\
3^2 >0 \text{  and  } 2(3)+3 > 0 \color{Cerulean}{✓} \quad & \quad (-1)^2 > 0  \text{  and  } 2(-1)+3 > 0 \color{Cerulean}{✓} && \text{Check the solution when substituted in the arguments is }> 0
\end{align*}\]

Analysis

There are two solutions: \(3\) or \(−1\). The solution \(−1\) is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.

 Try It \(\PageIndex{12}\)

Solve \(\ln(x^2)=\ln1\).

Answer

\(x=1\) or \(x=−1\)

Key Equations

One-to-one property for exponential functions	For any algebraic expressions \(S\) and \(T\) and any positive real number \(b\), where \(b^S=b^T\) if and only if \(S=T\).
Definition of a logarithm	For any algebraic expression S and positive real numbers \(b\) and \(c\), where \(b≠1\), \({\log}_b(S)=c\) if and only if \(b^c=S\).
One-to-one property for logarithmic functions	For any algebraic expressions \(S\) and \(T\) and any positive real number \(b\), where \(b≠1\), \({\log}_bS={\log}_bT\) if and only if \(S=T\).

Key Concepts

• We can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then we use the fact that exponential functions are one-to-one to set the exponents equal to one another and solve for the unknown.
• When we are given an exponential equation where the bases are explicitly shown as being equal, set the exponents equal to one another and solve for the unknown. 
• When we are given an exponential equation where the bases are not explicitly shown as being equal, rewrite each side of the equation as powers of the same base, then set the exponents equal to one another and solve for the unknown. 
• When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side. 
• We can solve exponential equations with base \(e\), by applying the natural logarithm of both sides and then using the fact that \( \ln (e^U) = U \). 
• After solving an exponential equation, check each solution in the original equation to find and eliminate any extraneous solutions (Specifically, \(b^p\) is ALWAYS positive). 
• When given an equation of the form \({\log}_b(S)=c\), where \(S\) is an algebraic expression, we can use the definition of a logarithm to rewrite the equation as the equivalent exponential equation \(b^c=S\), and solve for the unknown. 
• When given an equation of the form \({\log}_bS={\log}_bT\), where \(S\) and \(T\) are algebraic expressions, we can use the one-to-one property of logarithms to solve the equation \(S=T\) for the unknown. Check that the answers do not make any original log arguments zero or negative.

Contributors

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.